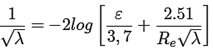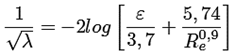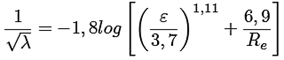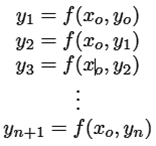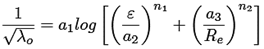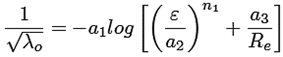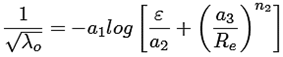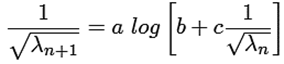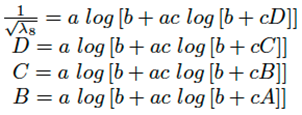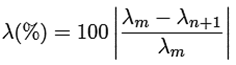Introducción
En los sistemas de redes de tuberías de procesos industriales, el comportamiento del flujo interno presenta fluctuaciones de velocidad, presión, temperatura, entre otros parámetros, el flujo se impulsa mediante la diferencia de presión, y la fricción del flujo está presente.
Para una tubería o instrumento de medición, existe un gradiente de presión, velocidad, temperatura; la velocidad del flujo es máxima en la región central y en la pared la velocidad se considera nula por la condición de no deslizamiento. Por tanto, una caída de presión ocasionada por esfuerzos viscosos representa una pérdida de presión irreversible llamada pérdida de presión [1, 2]. Por ejemplo, en equipos experimentales de medición de caudal, tales como para el caso de un tubo Venturi, las caídas de presión en la sección de la garganta son abruptos, y en las paredes de las uniones de la sección de la garganta con las secciones convergentes y divergentes presentan menores caídas de presión con respecto a la región central del flujo [3].
El régimen de flujo se clasifica en laminar, transición y turbulento. Para el caso de flujo laminar, se caracteriza por líneas de corriente suaves y paralelas con movimiento ordenado, y es común en fluidos con alta viscosidad y con movimiento a baja velocidad. Mientras que el flujo turbulento se caracteriza por fluctuaciones aleatorias de remolinos a diferentes escalas. Estos remolinos transportan masa, cantidad de movimiento y energía a otras regiones del flujo, por lo que las regiones afectadas presentan aumento de cantidad de movimiento, de masa y transferencia de calor. En consecuencia, el flujo turbulento está relacionado con variaciones de valores muy altos de coeficientes de fricción, transferencia de masa y transferencia de calor [1, 2].
Osborne Reynolds [4] realizó experimentos para el flujo en secciones de tuberías y descubrió que el régimen de flujo está relacionado con la razón de las fuerzas inerciales sobre las fuerzas viscosas en el fluido. La razón de las fuerzas es nombrada número de Reynolds, R e , y se expresa como R e = V d/ν, donde V es la velocidad promedio, d es el diámetro interno de la tubería, ν = μ/ρ es la viscosidad cinemática, μ es la viscosidad dinámica y ρ la densidad del fluido [1, 2].
La transición de flujo laminar a turbulento depende de la viscosidad y velocidad del flujo, así como de la geometría de la tubería, la rugosidad de la pared interna, la temperatura de la pared, entre otros factores. En la mayoría de las condiciones prácticas, el flujo se clasifica como flujo laminar para R e ≤ 2300, flujo turbulento para R e ≥ 4000 y flujo en transición en el rango de 2300 ≤ R e ≥ 4000 [1, 2].
Colebrook y White [5, 6] propusieron una ecuación implícita para el cálculo del factor de fricción, λ, del flujo turbulento en tuberías, basado en sus resultados de sus investigaciones experimentales, la cual se expresa como la ecuación de Colebrook-White (1):
(1)
La ecuación de Colebrook-White es una combinación de datos para flujo en transición y turbulento en tuberías lisas y rugosas. El parámetro ε es la rugosidad relativa, y se define como ε = k/d; donde k es la altura promedio de la rugosidad del material y d el diámetro interno de la tubería; y el parámetro R e es el número de Reynolds. Señalando que, los parámetros λ, ε y R e son adimensionales.
El factor de fricción de la ecuación de Colebrook-White no se puede despejar aplicando procedimientos algebraicos para obtener una solución exacta y explícita, en consecuencia, el factor de fricción se determina por métodos numéricos aplicando procedimientos iterativos en códigos computacionales, tales como el método de Newton-Raphson, bisección, punto fijo, entre otros. Por tanto, en el diseño de redes de tuberías se dificulta obtener el factor de fricción debido a los laboriosos cálculos por métodos iterativos.
Como solución alternativa a la ecuación implícita de Colebrook-White, Moody [7] propuso una expresión gráfica de dicha ecuación, la cual es un diagrama utilizado en ingeniería para obtener el factor de fricción. Sin embargo, para determinar el factor de fricción se genera un error numérico, por lo cual el resultado es aproximado.
En la literatura se reportan correlaciones empíricas que son explícitas para el cálculo del factor de fricción como solución aproximada, donde las estructuras de las relaciones empíricas se basan en la ecuación de Colebrook-White. Las ecuaciones empíricas más conocidas y utilizadas son la ecuación (2) de Swamee- Jain [8], que tiene un error máximo estimado de 3,2 %, y la ecuación (3) de Haaland [9] que tiene un error máximo estimado de 2,1 %.
(2)
(3)
Con el propósito de reducir el error numérico del factor de fricción en función de ε y R e , diferentes autores han propuesto relaciones empíricas y explícitas, para lo cuales han aplicado diferentes métodos para obtener la solución.
Se nombran algunos autores, tales como Mikata y Walczack [10], Rollmann y Spindler [11] y Biberg [12] que aplican la función ω de Lambert. Serghides [13], Vatankhah [14] y Azizi et al. [15] obtienen correlaciones mediante combinaciones de procedimientos algebraicos. Chen [16], Schorle et al. [17], Zigrang y Sylvester [18], Sousa et al. [19], Romeo etal. [20] y Offor y Alabi [21] obtienen correlaciones mediante el método recursivo con modificaciones de las constantes y exponentes. Así como, Santos et al. [22] y Alfaro et al. [23] realizan evaluaciones experimentales para el cálculo del factor de fricción.
Además de los autores antes señalados, Pérez et al. [24] reportan una lista de cuarenta y nueve (49) relaciones explícitas para el cálculo del factor de fricción. La lista comienza con la ecuación de Moody [7] y termina con la de Azizi et al. [15].
Cabe señalar que estudios recientes presentan revisiones de errores del factor de fricción para algunas correlaciones reportadas en la literatura [25], y exponen que la relación propuesta por Praks y Brkić [26] arroja un máximo error porcentual de 0,001204 %, la relación propuesta por Serghides [13] arroja 0,00256 %; la relación propuesta por Vantakhak [14] arroja 0,005952%, y la relación propuesta por Romeo et al. [20] arroja 0,007468 %. Mientras que, Lamri y Easa [27] aplican el teorema de inversión de Lagrange, y para cuatro términos obtienen el error de 0,002 %.
De los resultados reportados por los autores señalados, el error producido por cada ecuación empírica se debe a la forma en que se estructura la ecuación con los términos algebraicos que lo componen, así como por los coeficientes y exponentes.
La precisión numérica en la cantidad de dígitos de los decimales del factor de fricción está relacionada con el error relativo porcentual, por lo que es importante la calibración de los coeficientes y exponentes para una nueva correlación empírica y que sea simple en toda su estructura como modelo matemático.
En el presente trabajo se construye una correlación explícita que está basado en el método recursivo, para el cálculo del factor de fricción de flujo turbulento en tuberías. Así también se evalúa la correlación para cuatro relaciones explícitas que calculan el factor de fricción para la primera aproximación inicial. En la sección 2 se presenta la metodología; en la sección 3 se presentan los resultados obtenidos del factor de fricción y los errores porcentuales; seguidamente, en la sección 4 se exponen las conclusiones del análisis realizado.
Materiales y métodos
Representación gráfica del ajuste de la curva de correlación
La Figura 1 muestra un esquema genérico para tres trayectorias de curvas. Se ilustra la curva de una función analítica implícita y = f(x, y); la curva de una función empírica explícita y = h(x), que está desfasada de la curva de la función analítica. La curva segmentada corresponde a la correlación, la cual es la función de recursión y n +1 = f(x, yn), y esta función está próxima a la curva de la función analítica.
En un punto local de referencia (x o , y o ) para la función empírica y o = h(x o ), los datos x o están dentro del rango desde x a hasta x b (eje x), y los datos de salida y o está dentro del rango desde y a hasta y b (eje y). Para la función analítica, para x o , el dato de salida es y m , siendo el punto de referencia (x o , y m ). Asimismo, para la recursión, para el dato x o , el dato de salida es y n+1 , siendo la posición de referencia (x o , y n+1 ). Para un punto fijo x o, a medida que se incrementa los términos algebraicos de la recursión y n+1 , la cual inicia a partir de y o , la variable dependiente y n+1 se aproxima a y m el cual es un dato fijo, por tanto, el error numérico se reduce progresivamente hasta lograr la convergencia numérica y m = y n+1 . Por tanto, para un barrido de datos de entrada x o, la curva de la recursión quedaría superpuesta sobre la curva analítica en el rango de x a ≤ x o ≤ x b , y los datos de salida en el rango de y a ≤ y n+1 ≤ y b .
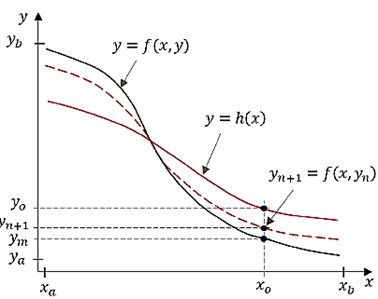
Figura 1 Esquema básico de representaciones de las curvas de la función analítica, empírica y de la recursión
De manera general, para el esquema de la Figura 1, los pasos del método recursivo son los que se muestran en la ecuación (4).
(4)
Donde la primera aproximación es y 1 , la segunda es y 2 , la tercera y 3 , y la última es y n+1 ; siendo de manera creciente la sucesión para y n+1 , el cual inicia desde n = 0.
La función y o = h(x o ) es una representación matemática de una expresión que está explícita, la cual permite el cierre como primer cálculo inicial, siendo y o la primera solución aproximada.
Relación explícita
Para el cálculo de la primera aproximación inicial del factor de fricción λo, es necesario establecer una expresión matemática como una relación explícita para dicha solución aproximada.
En ese sentido, para obtener la relación explícita λo se tomó en cuenta la ecuación (1) de Colebrook-White [5,6]. Al argumento de la ecuación de Colebrook-White se le eliminó λ , y se acondicionaron las ubicaciones de los coeficientes a i y exponentes n i . De manera que, la relación explícita λo para el primer cálculo del factor de fricción se estructuró como la ecuación (5).
(5)
Los datos de entrada son los parámetros independientes: la rugosidad relativa ε y el número de Reynolds R e , y se establecieron en el rango de 1 × 10−06 ≤ ε ≤ 0, 05 y 4000 ≤ R e ≤ 1 × 10+08. Y el dato de salida es λo.
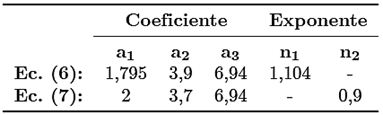
Los coeficientes a 1 , a 2 , a 3 y los exponentes n 1 y n 2 de la ecuación (5) fueron calibrados de manera iterativa en una hoja de cálculo de Excel 2019, tomando como datos patrón la ecuación (1) de Colebrook-White. Se consideraron los mejores resultados de las magnitudes de los coeficientes y de los exponentes para el establecimiento de dos relaciones explícitas.
En la Tabla 1 se presentan las magnitudes de los coeficientes y exponentes, para las dos relaciones explícitas que se proponen, las cuales se presentan como las ecuaciones (6) y (7).
(6)
(7)
Acondicionamiento de la correlación
Basado en el método recursivo, a la ecuación (1) de Colebrook-White [5,6] se le acondicionó para el cálculo del factor de fricción como dato de salida λ n+1 , y como dato de entrada λn, la cual se expresa como la ecuación (8).
(8)
Donde a = −2, b = ε/3, 7 y c = 2, 51/R e .
La ecuación (8) está basada en el logaritmo de base 10, la cual se emplea en los cálculos del presente trabajo. También, se puede expresar en función del logaritmo natural, siendo 1/ λ 𝑛+1 = a1In[b+c/ λ 𝑛 ], donde a1 = a/ln (10).
Con la ecuación (8) se estructuró la correlación expresada como la ecuación (9) para el cálculo de incrementos de la sucesión λn+1 = λ2, λ4, λ6, λ8.
(9)
Siendo D= 1 λ 6 , C= 1 λ 4 , B= 1 λ 2 y A= 1 λ 0 .
Adicionalmente, a la ecuación (9) se le incrementó los términos para evaluar hasta λn+1 = λ20, mas no se presenta la expresión matemática para λ20 por ser el procedimiento similar. Ya que, de manera general, se aplica el mismo principio de la ecuación (8).
El propósito de evaluar la correlación de manera segmentada fue para determinar la tendencia en la disminución del error porcentual del factor de fricción para diferentes valores del número de Reynolds y de la rugosidad relativa.
Como dato de entrada de λo para A = 1/ λ 0 en la ecuación (9), se tomó en cuenta cuatro relaciones explícitas: la relación de Swamee-Jain [8] (ecuación (2)), la de Haaland [9] (ecuación (3)), así como, las ecuaciones (6) y (7) que se proponen en el presente trabajo. Donde, cada relación se evaluó de manera separada en la ecuación (9).
El cálculo del error porcentual del factor de fricción λ(%) se determinó con la siguiente ecuación (10).
(10)
Donde λm es el factor de fricción de la solución exacta de la ecuación de Colebrook-White, y λn+1 es el factor de fricción de la ecuación (9).
Cabe señalar, que todos los cálculos numéricos y gráficas fueron realizadas en una hoja de cálculo de Excel 2019.
Resultados y discusión
Correlación y relaciones explícitas para el cálculo del factor de fricción
La correlación construida por el método recursivo está expresada como la ecuación (9), siendo a = −2, b = ε/3, 7, c = 2, 51/R e . Esta correlación es una expresión matemática que modela la trayectoria de la curva del factor de fricción, λ, en función de la rugosidad relativa, ε, y el número de Reynolds, R e . Siendo el término A = 1/ λ 0 , y en la cual se sustituyen las relaciones explícitas de la forma 1/ λ 0 que actúan como cierre de la correlación. Las dos relaciones explícitas que se proponen en el presente trabajo para el cierre de la ecuación (9), son las ecuaciones (6) y (7).
Cabe señalar, que la ecuación (9) es simple en su estructura para cálculos directos, la cual mejora la respuesta en la disminución del error del factor de fricción para cada incremento de términos en la recursión, por tanto, los dígitos decimales exactos del factor de fricción se incrementan.
A continuación, se presentan los errores porcentuales del factor de fricción que arroja la ecuación (9), para las relaciones explícitas que actúan como cierre para A = 1/ λ 0 , la ecuación (2) de Swamee-Jain, la ecuación (3) de Haaland, y las ecuaciones (6) y (7) que se proponen.
Errores porcentuales del factor de fricción
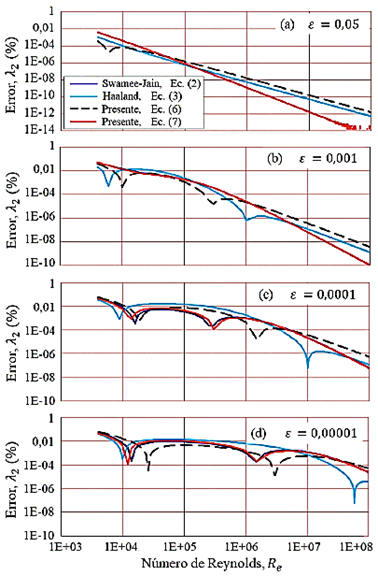
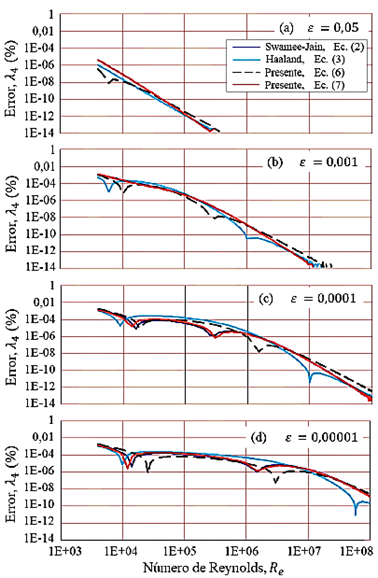
Las gráficas de las trayectorias de las curvas de los errores porcentuales del factor de fricción λo, como cálculo de la primera aproximación inicial para las ecuaciones (2), (3), (6) y (7) se muestran en la Figura 2. Las trayectorias de las curvas son fundamentales, en primera instancia, para comprender el efecto que tienen los coeficientes y exponentes para valores variables de la rugosidad relativa, ε, y el número de Reynolds, R e .
Para el rango del número de Reynolds 4000 ≤ R e ≤ 1 × 1008 y el rango de la rugosidad relativa 1 × 10−06 ≤ ε ≤ 0, 05, la ecuación (6)) presenta el error porcentual máximo estimado de 2,1 % y la ecuación (7)) el error de 3,1 %. Mientras que, la ecuación (2) de Swamee-Jain presenta el error máximo estimado de 3,2 % y la ecuación (3) de Haaland el error de 2,1 %. En ciertas regiones, las ecuaciones (2), (3), (6) y (7) presentan errores alrededor de 0,1 % (Figura 2). Cabe señalar que las figuras solo muestran las trayectorias de las curvas para el rango de la rugosidad relativa 0, 00001 ≤ ε ≤ 0, 05.
Para ε = 0, 05 (Figura 2a) las ecuaciones (3) y (7) presentan trayectorias con tendencia horizontal a partir de la posición local R e = 1×1005. Mientras que, la curva de la ecuación (7) se superpone a la curva de la ecuación (2) y tiene una tendencia de una recta con pendiente negativa. Para ε = 0, 00001 (Figura 2d) las fluctuaciones de las curvas del factor de fricción son mayores con respecto a las otras curvas ilustradas en la misma Figura 2.
Se puede observar que para tubos hidráulicamente rugosos (ε = 0, 05) las tendencias distan entre sí mucho más que en tubos hidráulicamente lisos (ε = 0, 00001), sobre todo, las ecuaciones (2) y (7) para la curva de la Figura 2a.
Las curvas muestran que los coeficientes y exponentes de cada una de las relaciones tienen un efecto dominante que definen su propio comportamiento de trayectoria.
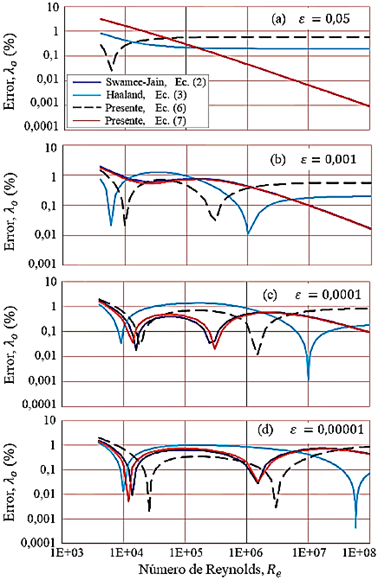
Figura 2 Errores porcentuales del factor de fricción para λo, como cálculo de la primera aproximación de las ecuaciones (2), (3), (6) y (7)
Cabe señalar, para la Figura 2 y otras figuras siguientes que se señalan más adelante, en los picos descendentes para determinados números de Reynolds, allí se presentan puntos de inflexión de las curvas y las mismas no se pueden apreciar, porque los datos de salida de los errores (eje y) están en valores absolutos de acuerdo con la ecuación (10). También es importante destacar que el eje vertical está a escala logarítmica de base 10, y esto fue debido para lograr que las trayectorias de las curvas puedan ser analizadas.
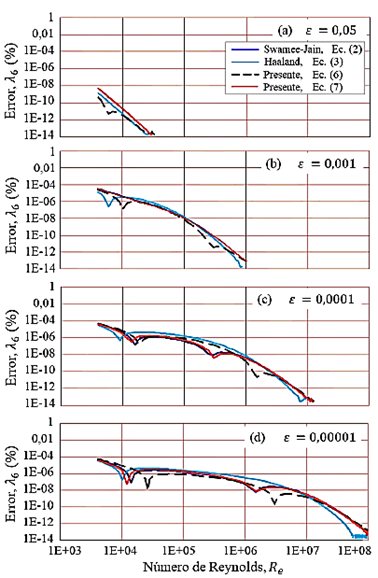
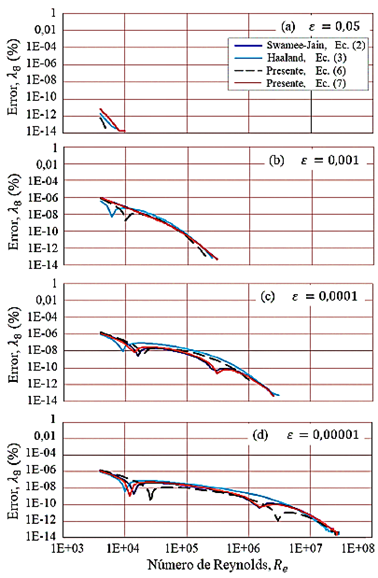
Con respecto a las trayectorias de las curvas de los errores porcentuales del factor de fricción para λ2, λ4, λ6 y λ8 se muestran en las Figuras 3, 4, 5 y 6. Se observa que para las ecuaciones (2), (3), (6) y (7) definen trayectorias de sus propias curvas a medida que se incrementan los términos. Para cada valor de ε, en la posición Re = 4000, para λ2, λ4, λ6 y λ8, allí las trayectorias de las curvas presentan el mayor error relativo porcentual del factor de fricción.
Las regiones para los máximos errores del factor de fricción se presentan para las posiciones locales ε = 0, 00001 y R e = 4000, tal como se muestran en las Figuras 3d, 4d, 5d y 6d.
Las ecuaciones (2), (3), (6) y (7) para λ8 (Figura 6d) tienen errores menores de 0,000002%. Mientras que, para λ6 (Figura 5d) se presenta errores máximos de 0,00006%. Para λ4 (Figura 4d) se presenta errores de 0,002%, y para λ2 (Figura 3d) presenta errores de 0,061%.
Se evidencia que las magnitudes de los coeficientes y exponentes para cada relación explícita tienen un comportamiento particular, y evoluciona la trayectoria de las curvas a medida que se incrementa la rugosidad relativa para el mismo rango de número de Reynolds, tal como se muestran en las Figuras del 2 al 6. Sería de interés, en trabajos posteriores, que se realicen comparaciones con otras relaciones explícitas, sustituyendo en la ecuación (9), para determinar con cuál de ellas se obtendría menores errores porcentuales.
Cabe señalar, algo parecido con la Figura 2a ocurre para la Figura 3a, para λ2 y ε = 0, 05, para las ecuaciones (2) y (7) que difiere más en tubos hidráulicamente rugosos, con una tendencia de curvas rectas con pendiente negativa. Así como, las ecuaciones (3) y (6) también presentan curvas rectas, y se interceptan en la región alrededor de R e = 1 × 1005. También ocurre para las Figuras 4a, 5a y 6a, que tienen trayectorias con tendencia de curvas rectas para tuberías rugosas (ε = 0, 05), respectivamente.
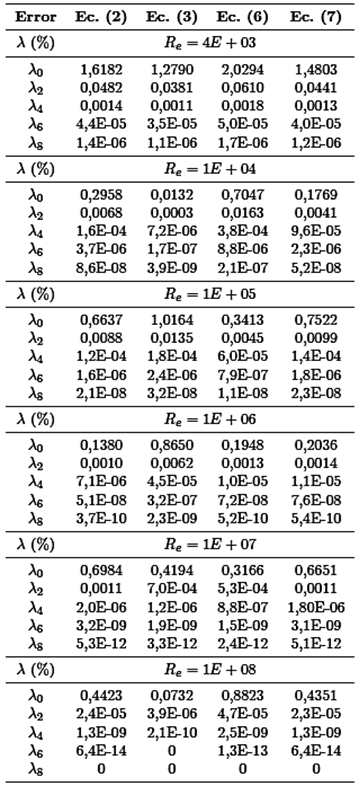
La Tabla 2 presenta los errores máximos del factor de fricción para ε = 0, 00001 y los números de Reynolds locales 4 × 1003, 1 × 1004, 1 × 1005, 1 × 1006, 1×1007 y 1×1008, para λo, λ2, λ4, λ6 y λ8, las cuales están relacionadas con las Figuras 2, 3, 4, 5 y 6. Para la ecuación (6) y λ8, y las condiciones ε = 0, 00001 y R e = 4 × 1003, el error porcentual máximo del factor de fricción es 1, 7 × 10−06 %. Para las ecuaciones (2), (3) y (7), los errores son menores de 1, 7 × 10−06 %.
Cabe señalar que a medida que se incrementa la recursión, disminuyen los errores porcentuales, en consecuencia, los factores de fricción para λ8 presentan siete dígitos decimales exactos para ε = 0, 001, ocho dígitos exactos para ε = 0, 00001 y nueve dígitos exactos para ε = 0, 05 y ε = 0, 0001, con respecto al factor de fricción de la ecuación (1) de Colebrook-White, tal como se muestran en la Tabla 3. Para recursiones menores de λ8, los decimales exactos disminuyen; para λ6 es igual a seis dígitos exactos, para λ4 es igual a cinco dígitos exactos, así como para λ2 es igual a cuatro dígitos exactos.
Para la ecuación (9) y λ8 se obtuvo el mayor error porcentual máximo del factor de fricción de 0,0000017%; el cual está muy por debajo de los errores porcentuales reportados por Brkić y Stajić [25], quienes, Praks y Brkić [26] obtuvieron errores alrededor de 0,001204% y, Serghides [13] obtuvo el error de 0,002560%. Cabe señalar que los errores porcentuales reportados por Brkić y Stajić [25] no han sido verificados mediante cálculos numéricos por los autores del presente trabajo, en ese sentido, solo se expone con fines comparativos.
Tabla 2 Errores porcentuales, λ (%), del factor de fricción de las recursiones, para ε = 0, 00001 y R e locales.
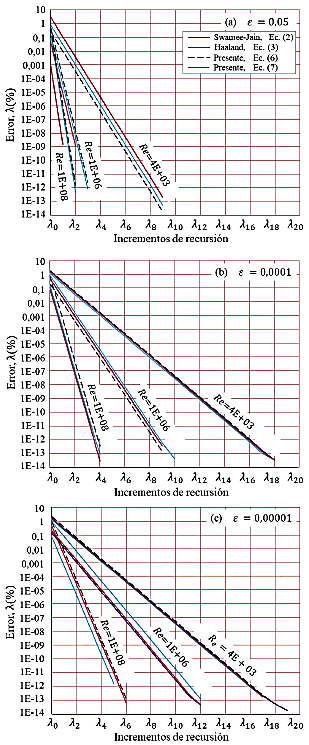
La Figura 7 muestra la disminución del error porcentual del factor de fricción a medida que se incrementa la recursividad para λ2, λ4, λ6, λ8, hasta λ20.
Para las ecuaciones (2), (3), (6) y (7), ε = 0, 00001 y posición local R e = 4E + 03, la magnitud de λ9 reporta el error porcentual de 2, 85E−07 %, λ10 reporta 4, 95E − 08%, λ11 reporta 8, 55E − 09%; λ12 reporta 1, 5E − 09%, λ14 reporta 4, 5E − 11%, λ16 reporta 1, 5E − 12%, λ18 reporta 5, 5E − 14%, y por último λ20 reporta el error de 0,0 %.
Para otros valores de rugosidad relativa y números de Reynolds, los errores porcentuales del factor de fricción son menores. En la cual se evidencia que a medida que se incrementa el número de Reynolds se requiere de menos términos en la recursión para la convergencia numérica.
Tabla 3 Comparación de valores numéricos de factores de fricción de las recursiones con respecto a la ecuación (1) de Colebrook-White, para R e = 4E + 03 y ε locales.

Para tuberías hidráulicas con valores menores de ε = 0, 00001, incluso para ε = 0, la ecuación (9) es aplicable. Al sustituir ε = 0, la ecuación (9) se simplifica, y numéricamente las curvas de los errores del factor de fricción son parecidas a las trayectorias de las curvas mostradas en la Figura 7c; y los resultados de las gráficas y tablas no se presentan por ser casi similares. Donde, para λ8, para el rango de 4000 ≤ Re ≤ 1E+08, el error porcentual es menor de 1,5E-06 %.
Las ecuaciones de Swamee-Jain y Haaland fueron evaluadas en la ecuación (9), a partir de λ2, las cuales arrojan resultados similares con respecto a las evaluaciones de las ecuaciones (6) y (7) que se proponen.
En ese sentido, cualquier ecuación que tenga estructuras diferentes a las ecuaciones (6) y (7) y que las mismas sean utilizadas en la ecuación (9), pueden reducir su error porcentual del factor de fricción.
La ventaja de la ecuación (9) radica en la simplicidad de su construcción y su fácil uso para calcular directamente el factor de fricción como una solución aproximada.
Conclusiones
Basándose en los análisis realizados, se concluye que:
La correlación expresada como la ecuación (9) para λ8, y las relaciones explícitas que actúan como cierre que son expresadas como las ecuaciones (6) y (7) para el cálculo de λo como aproximación inicial, satisfacen como solución aproximada para la solución de la ecuación (1) implícita de Colebrook-White. La ecuación (9) es aplicable para el flujo turbulento dentro del rango estudiado del número de Reynolds 4000 ≤ Re ≤ 1E + 08 y rugosidad relativa 0, 05 ≥ ε ≥ 0, 00001; y como una extensión del estudio realizado, es posible su aplicación para tuberías lisas dentro del rango de número de Reynolds antes señalado. Así como, se acotacota que la ecuación (9) no es aplicable para Re < 4000.
Dentro del rango de la rugosidad relativa, 0, 05 ≥ ε ≥ 0, 00001, y número de Reynolds, 4 × 1003 ≤ R e ≤ 1 × 1008, el error porcentual máximo del factor de fricción reporta un valor estimado de 1, 7 × 10−06 %, para ε = 0, 00001 y R e = 4 × 1003. Donde el factor de fricción tiene siete dígitos decimales exactos. Para otros valores de la rugosidad relativa y números de Reynolds, las magnitudes numéricas del factor de fricción presentan más de siete dígitos decimales exactos.
Asimismo, para recursiones mayores de λ8, los dígitos decimales exactos se incrementan. Para ε = 0, 00001 y Re = 4×1003, λ10 reporta el error de 4, 95×10−08%, λ14 reporta 4,5 × 10−11%, y, finalmente, para λ20 reporta el error de 0,0%.