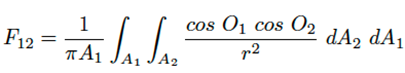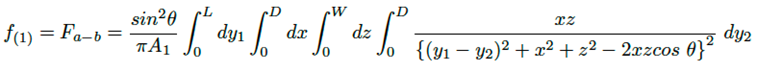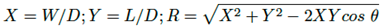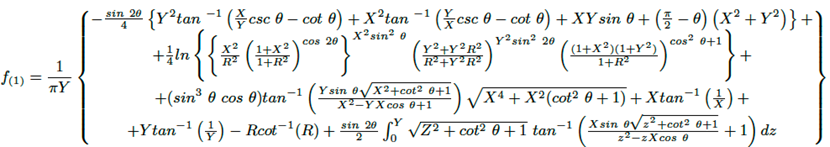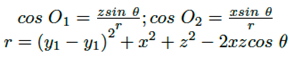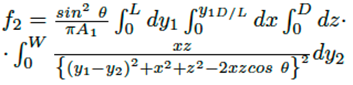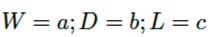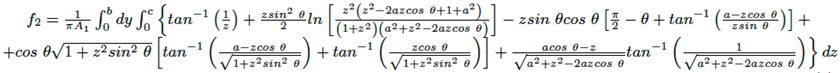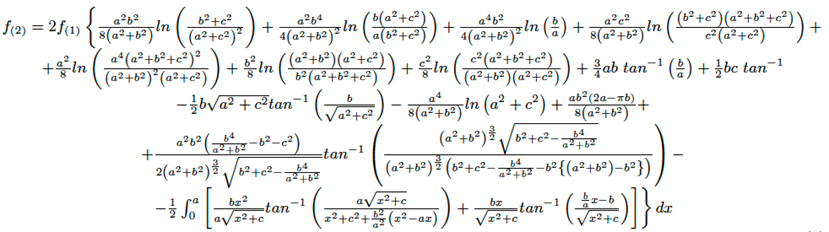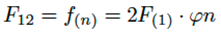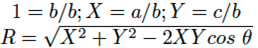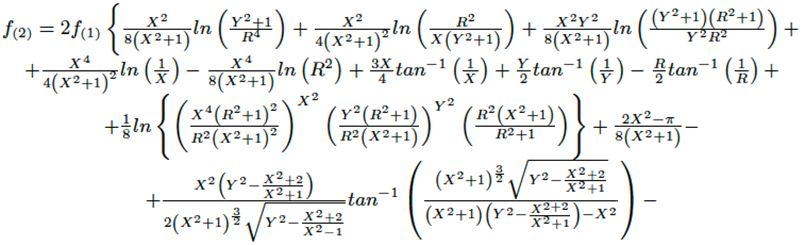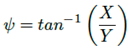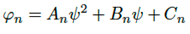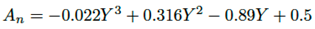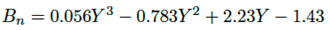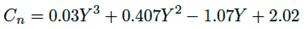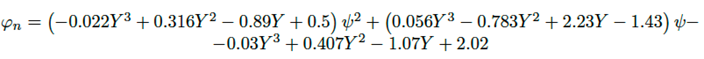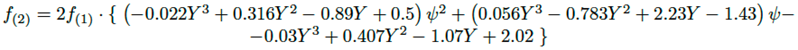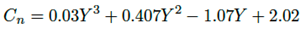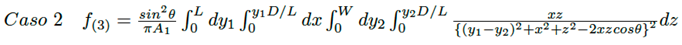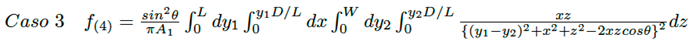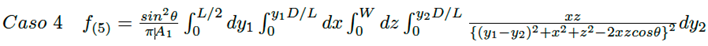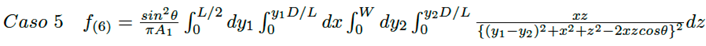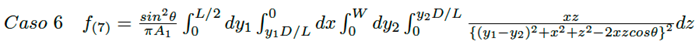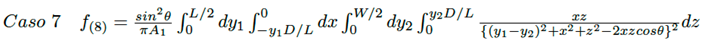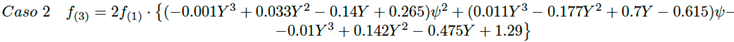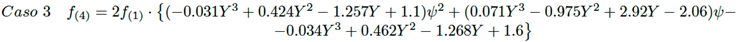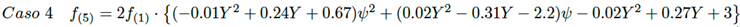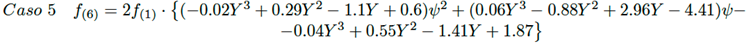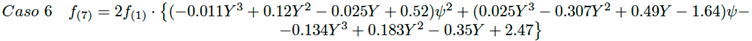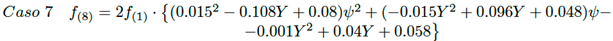Introducción
En la ingeniería térmica es requerido evaluar la radiación térmica entre superficies. El factor de visión es quien establece que fracción de la energía radiante emitida por una superficie es interceptada por otra [1].
La relación geométrica entre dos superficies y su influencia sobre el factor de visión ha sido objeto de estudio durante décadas, siendo obtenidas soluciones numéricas y analíticas para disímiles configuraciones geométricas [2-5]. Una compilación extensa de factores de visión, con más de 320 configuraciones diferentes, fue dada por Howell [6].
El salto acelerado del uso de las técnicas computacionales ha generalizado el uso de programas comerciales basados sobre el método de elementos finitos (MEF) en la solución de problemas de radiación térmica [7-10].
Los problemas tridimensionales de bordes se reducen a superficies con bordes comunes y ángulo incluido. Sin embargo, para este tipo de geometrías el uso del álgebra de factores de forma es muy tedioso, siendo preferidas las soluciones numéricas, entre ellas el MEF [11-13].
En el MEF, los mallados generalmente utilizan elementos triangulares y raramente usan rectángulos o cuadrados, a menos que la geometría global sea un cubo perfecto. La determinación de una solución analítica para el factor de visión entre geometrías triangulares requiere de sumas de integrales múltiples, debido al cambio de los contornos de integración. Las soluciones en muchos casos no son funciones elementales, siendo requerido manipular funciones trigonométricas inversas, polilogaritmos y sumas de series infinitas [14].
Esto propicia que la integración directa sea una tarea extremadamente engorrosa para geometrías no compartidas o sin bordes comunes, lo cual hace preferir la integración numérica. Por este motivo, se carece de soluciones analíticas para este tipo de geometrías [15].
Mediante RMS con cinco intervalos, fueron graficados los factores de visión para varias geometrías triangulares perpendiculares y con borde común [16]. Sin embargo, su interpretación gráfica genera errores medios del 12 %, además de no ser aplicables al MEF, pues no pueden ser discretizados. Actualmente, en la literatura técnica especializada, para obtener los factores de visión entre geometrías triangulares solo se dispone de esta solución gráfica [6-13].
El método de RCB brinda un ajuste razonable durante la aproximación de funciones complejas, por tal motivo puede ser utilizado para generar las expresiones requeridas en la discretización del MEF. El método RCB es similar al MEF, pues su concepción matemática se basa en la formación de nodos, obteniéndose los ajustes con polinomios a partir de la interconexión de los nodos [17]. A partir de lo anteriormente planteado, se muestra que en la actualidad se carece de soluciones analíticas (exactas o aproximadas) para la estimación de los factores de visión entre las geometrías triangulares con bordes comunes y ángulo ( incluido.
Por tanto, el objetivo principal de este trabajo es desarrollar soluciones aproximadas para el cálculo de los
factores de visión entre geometrías triangulares con bordes comunes y ángulo ( incluido, que no muestren una alta complejidad matemática y garanticen un ajuste adecuado respecto a la SA. Así es posible establecer un nuevo método de análisis, para su uso en el MEF.
En esta investigación, se desarrollan las soluciones analíticas exactas para ocho geometrías triangulares básicas y sus respectivas RCB. Para establecer comparaciones se calcularon 42 ejemplos con varias relaciones de aspecto para cada geometría, usando la SA, la RCB y la RMS.
Dado el carácter práctico de la contribución y los valores razonables de los ajustes obtenidos, la propuesta es una herramienta adecuada para su aplicación a la ingeniería térmica y prácticas afines que requieren cálculos de radiación térmica entre geometrías triangulares.
Materiales y métodos
Definición del factor de visión
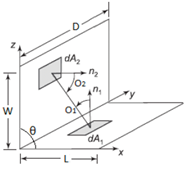
El factor de visión F12 depende de la posición y configuración geométrica de las superficies emisora A1 y receptora A2, pudiendo ser definido como la fracción de la radiación que abandona la primera y que es interceptada por la segunda, lo cual es expresado como [18], en la ecuación (1) .
(1)
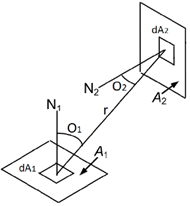
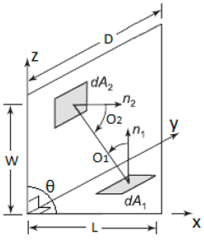
Donde: O1, O2− ángulos entre el vector normal a las áreas dA1 y dA2 y la línea que conecta el centro de las superficies A1 y A2, respectivamente. r-distancia entre los centros de las superficies A1 y A2, (véase la Figura 1).
La ecuación (1) requiere una doble integración sobre las superficies, lo cual resulta ser muy laborioso, pues se debe manipular un grupo elevado de integrales inmediatas y su posterior factorización.
El análisis puede ser simplificado mediante aproximaciones numéricas, pues con un grupo razonable de intervalos, puede ser obtenido un ajuste adecuado. Para configuraciones tridimensionales (3-D), en la actualidad se disponen de varios métodos de solución, entre ellos la integración de contorno [19-24].
En este trabajo, será utilizada la integración de contorno para obtener del factor de visión de las ocho geometrías analizadas. Para aproximar las funciones especiales generadas en la integración, será utilizado el método RCB.
Generado de mallas para elementos de superficies
En la ingeniería moderna, en la generación de mallas unos de los elementos más utilizados son los triangulares. Contrariamente, los rectangulares o cuadrados son utilizados en muy pocas ocasiones, exceptuando los casos que la geometría global sea un cubo perfecto. La formulación de este tipo de geometrías requiere un tratamiento matemático complejo que incluye sumas de la cuádruple integral ecuación (1), causado por la variación de los límites en la proyección sobre cada eje coordenado. El factor de visión entre dos superficies rectangulares del mismo ancho, con borde común y ángulo θ incluido (véase la Figura 2), viene dado por la ecuación (2).
(2)
Para evaluar la ecuación (2) son utilizadas las siguientes sustituciones (ecuación (3)).
(3)
Después de evaluar la ecuación (2) se obtiene la siguiente solución f(1) (ecuación (4)).
(4)
En las ecuaciones (2), (3) y (4), el ángulo θ es dado en radianes. La ecuación (4) es muy compleja, por esta razón, la última integral no fue resuelta, dado que su solución puede ser obtenida numéricamente usando la regla de Simpson 1/3 (con ocho intervalos como mínimo).
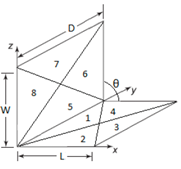
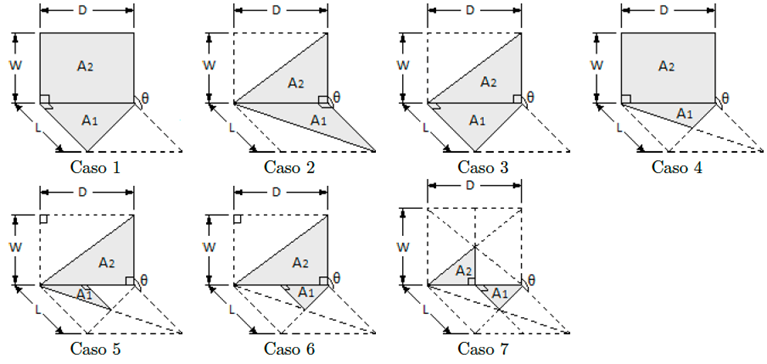
En la Figura 3, mediante el trazado de líneas diagonales, la superficie emisora A1 y receptora A2 son divididas en ocho geometrías triangulares. Aplicando el álgebra de forma para la geometría generada en la Figura 3, son obtenidas 1 2 n n−1 = 1 2 4 4−1 =32 combinaciones de factores de visión. La geometría analizada es simétrica, por tanto, es posible definir siete casos básicos (véase la Figura 4), los cuales serán:
Caso 1: Triángulo rectángulo a rectángulo, con lado común y ángulo θ entre ambas superficies.
Caso 2: Triángulo rectángulo a triángulo rectángulo, con lado común y ángulo θ entre ambas superficies: vértices en un punto común.
Caso 3: Triángulo rectángulo a triángulo rectángulo, con lado común y ángulo θ entre ambas superficies: vértices en extremos opuestos.
Caso 4: Triángulo isósceles a rectángulo, con lado común y ángulo θ entre ambas superficies.
Caso 5: Triángulo rectángulo a triángulo rectángulo de distinto tamaño, con ángulo θ entre ambas superficies: vértices en un punto común.
Caso 6: Triángulo rectángulo a triángulo rectángulo de distinto tamaño, con ángulo θ entre ambas superficies: vértices en extremos opuestos.
Caso 7: Triángulos rectángulos perpendiculares con un borde igual y dispuestos en dirección opuesta.
Los factores de visión para los restantes casos pueden ser obtenidos mediante la regla de sumas.
Modelación del factor de visión. Caso 1
En el caso 1 (véase la Figura 5), se cumple la ecuación (5).
(5)
Sustituyendo la ecuación (5) en la ecuación (1), el factor de visión F12 viene dado por la ecuación (6).
(6)
Para ejecutar la integración, en la ecuación (6) fue realizado el cambio indicado en la ecuación (7).
(7)
La ecuación (6) es integrada primero sobre la superficie emisora A1, obteniéndose una suma de integrales, la cual viene dada por la ecuación (8).
(8)
Después de un complejo proceso, en el que fue requerido resolver nn= 44 = 256 funciones primitivas, es resuelta la suma de integrales dobles dada en la ecuación (8), cuya solución es proporcionada en la ecuación (9):
(9)
En la ecuación (9), el término f(1) es obtenido mediante la ecuación (4). Dada la complejidad de la ecuación (9), la última integral no es resuelta, obteniéndose su solución de forma numérica mediante la RMS (se recomiendan doce intervalos). La ecuación (9) es transformada a la ecuación (10).
(10)
La ecuación (10) es posteriormente transformada, dividiendo cada variable dimensional por la longitud del borde común b, quedando de la forma de la ecuación (11).
(11)
Aplicando en la ecuación (9) el cambio de variables declarado en la ecuación (11), es obtenida la solución analítica para el caso 1, la cual viene dada por la ecuación (12).
(12)
La ecuación (12) es una combinación de variables (Y ;X) y su evaluación es una tarea compleja, al ser requeridos resolver polilogaritmos, sumas de series infinitas y funciones trigonométricas inversas. Sin embargo, mediante el método de raíces cruzadas de Bretzhtsov es posible obtener un resultado aproximado, lo cual simplificaría el cálculo del factor de visión.
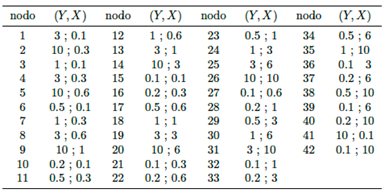
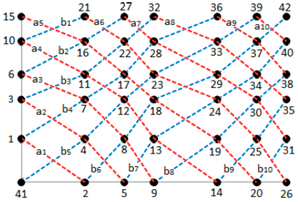
Para implementar el método de raíces cruzadas, son construidos los nodos usando valores prefijados (Y ;X), los cuales son unidos por medio de líneas diagonales formando las familias de curvas an y bn. En este trabajo son usados los valores Y = (0.1; 0.2; 0.5; 1; 3; 10) y X = (0.1; 0.3; 0.6; 1; 3; 6; 10).
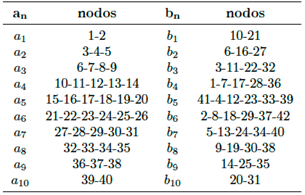
En las Tablas 1 y 2 son resumidos la combinación de variables (Y ;X) para cada nodo y los nodos que integran cada curva an y bn, respectivamente, mientras en la Figura 6 son graficadas las familias de curvas an y bn.
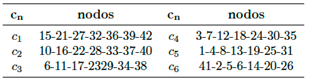
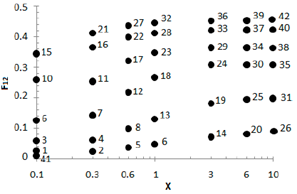
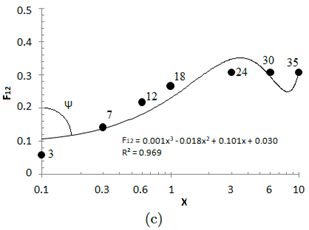
El siguiente paso es computar el factor de visión mediante la ecuación (12) para cada una de las combinaciones de variables (Y ;X) dadas en la Tabla 1, graficándolos en un diagrama F12;X, (véase la Figura 7). La unión de los nodos a lo largo del eje x permite crear una tercera familia de curvas cn. Una particularidad es que todos los nodos integrantes de una misma curva cn le corresponden el mismo valor de la variable Y (véase la Tabla 1). En la Tabla 3 son resumidos los nodos que integran cada curva cn.
Cada curva de las familias an, bn, cn es aproximada de forma individual mediante el método de mínimos cuadrados (MC), usando un polinomio de tercer grado en la forma mX3+nX2+oX+p, estableciendo así una dependencia entre el factor de visión F12 y la variable X. En la Figura 8 es dada la aplicación del método para las curvas a5, b5, c4.
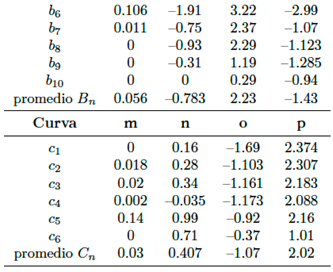
En la Tabla 4 son resumidos los valores de las constantes m,n,o,p obtenidos en la implementación de MC a la totalidad de las curvas an, bn, cn. En cada curva, los valores m, n,+o, p son promediados, obteniéndose de esta forma las funciones aproximadas An, Bn, Cn.
Para cada curva, el ángulo aparente de transmisibilidad (véase la Figura 8) es dado por la ecuación (13)
(13)
Por tanto, la raíz cruzada de Bretzhtsov es dada por la ecuación (14).
(14)
Las constantes m, n, o, p para los polinomios An, Bn, Cn son resumidos en la Tabla 4. Inicialmente para las aproximaciones fueron utilizadas las variables X, manteniendo constantes las variables Y , por tanto, para aplicar las raíces cruzadas, se alternan las variables Y por X, obteniéndose las ecuaciones (15), (16) y (17) para los polinomios An, Bn, Cn.
(15)
(16)
(17)
Sustituyendo las ecuaciones (15), (16) y (17) en la ecuación (14), se obtiene que la raíz cruzada de Bretzhtsov para el caso 1 viene dada por la ecuación (18).
(18)
Sustituyendo la ecuación (18) en la (10) es obtenido el factor de visión para el caso 1, el cual viene dado por la ecuación (19).
(19)
Resultados y discusión
Para el uso en la ingeniería práctica, la ecuación (19) es mucho más simple que la solución analítica (SA) dada con anterioridad en la ecuación (12). El porciento de desviación (error) es computado con respecto a la solución analítica y es obtenido mediante la ecuación (20) [25].
(20)
Donde: D% es el porciento de desviación, en %. SA es el factor de visión obtenido con la solución analítica. V al es el factor de visión obtenido mediante métodos aproximados.
Para calcular los valores de D%, son computados los factores de visión para todas las 42 combinaciones de variables (Y ;X) dadas en la Tabla 1, utilizando la SA, la RMS con cinco intervalos y los factores de visión obtenidos con la RCB.
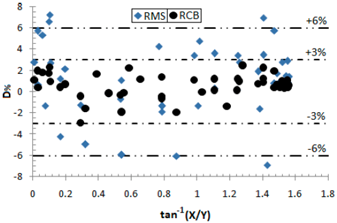
En la Figura 9 son graficados los valores D% obtenidos con la ecuación (18) para los factores de visión calculados mediante RMS y RCB, ajustados en bandas de error de ±3 % y ±6 %.
Para el caso 1, la Figura 9 muestra que las RCB proporcionan un mejor ajuste con respecto a la SA, con un error medio de ±3 % en el 100 % de los puntos (Y ;X) analizados. Contrariamente, los factores de visión obtenidos con RMS, brindan un menor ajuste con respecto a la SA, con errores medios de ±3 % y ±6 % para el 54,8 % y 85,7 % de los puntos (Y ;X) evaluados, respectivamente.
Modelación y validación de los casos 2 al 7
Para los casos 2 al 7 (véase la Figura 4), matemáticamente el factor de visión F12 viene dado por las ecuaciones (21) a la (26).
(21)
(22)
(23)
(24)
(25)
(26)
Las soluciones analíticas de las ecuaciones (21) a la (26) son extremadamente extensas y complejas, al ser requerido el manejo de funciones de Spence, función Gamma, sumas de polilogaritmos, funciones de Bessel modificadas de primera especie y órdenes cero, uno y dos, por esta razón, no serán presentadas acá.
Para la solución de las ecuaciones (21) a (26) se aplica el mismo procedimiento usado en el caso 1, obteniéndose para los casos 2 al 7 las siguientes aproximaciones para calcular el factor de visión.
(27)
(28)
(29)
(30)
(31)
(32)
En la Figura 10 son graficados en bandas de error de ±3 % y ±6 %, los D% obtenidos con la ecuación (18) para los factores de visión calculados con RMS y RCB para los casos 2 al 7.
Para el caso 2, la Figura 10 muestra que las RCB brindan el mejor ajuste con respecto a la SA, con un error medio de ±3 % en el 97.6 % de los puntos (Y ;X) analizados. Contrariamente, los factores de visión obtenidos con RMS, producen un menor ajuste con respecto a la SA, con errores medios de ±3 % y ±6 % en el 28,5 % y 64.3 % de los puntos (Y ;X) evaluados, respectivamente.
Para el caso 3, se comprueba en la Figura 10 que las RCB brindan un mejor ajuste con respecto a la SA, con errores medios de ±3 % y ±6 % en el 92.9 % y 100 % de los puntos (Y ;X) analizados, mientras que los factores de visión obtenidos con RMS proporcionan un menor ajuste con respecto a la SA, computando errores medios de ±3 % y ±6 % en el 38.1 % y 69.0 % de los puntos (Y ;X) evaluados, respectivamente.
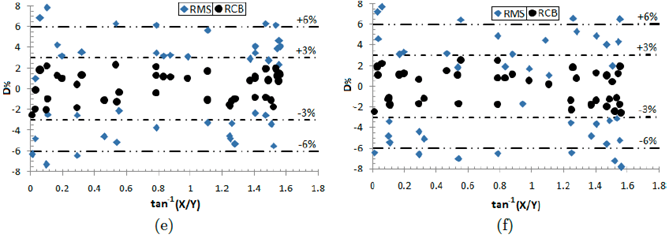

Figura 10 Valores D% obtenidos con la ecuación (18) para los casos analizados. (a) Caso 2; (b) Caso 3; (c) Caso 4; (d) Caso 5; (e) Caso 6; (f) Caso 7
Para el caso 4, la Figura 10 muestra que las RCB proporcionan un mejor ajuste con respecto a la SA, con errores medios de ±3 % y ±6 % en el 90.5 % y 100 % de los puntos (Y ;X) analizados. Contrariamente, los factores de visión obtenidos con RMS, brindan un menor ajuste con respecto a la SA, con errores medios de ±3 % y ±6 % en el 21.4 % y 61.9 % de los puntos (Y ;X) evaluados, respectivamente.
Para el caso 5, se comprueba en la Figura 10 que las RCB brindan un mejor ajuste con respecto a la SA, con errores medios de ±3 % y ±6 % en el 95.2 % y 100 % de los puntos (Y ;X) analizados, mientras que los factores de visión obtenidos con RMS proporcionan un menor ajuste con respecto a la SA, computando errores medios de ±3 % y ±6 % en el 26.2 % y 71.4 % de los puntos (Y ;X) evaluados, respectivamente.
Para el caso 6, la Figura 10 muestra que las RCB proporcionan un mejor ajuste con respecto a la SA, con errores medios de ±3 % en el 100 % de los puntos (Y ;X) analizados. Contrariamente, los factores de visión obtenidos con RMS, brindan un menor ajuste con respecto a la SA, con errores medios de ±3 % y ±6 % en el 31.0 % y 81.0 % de los puntos (Y ;X) evaluados, respectivamente.
Para el caso 7, se comprueba en la Figura 10 que las RCB brindan un mejor ajuste con respecto a la SA, con errores medios de ±3 % en el 100 % de los puntos (Y ;X) analizados, mientras que los factores de visión obtenidos con RMS proporcionan un menor ajuste con respecto a la SA, computando errores medios de ±3 % y ±6 % en el 23.8 % y 73.8 % de los puntos (Y ;X) evaluados, respectivamente.
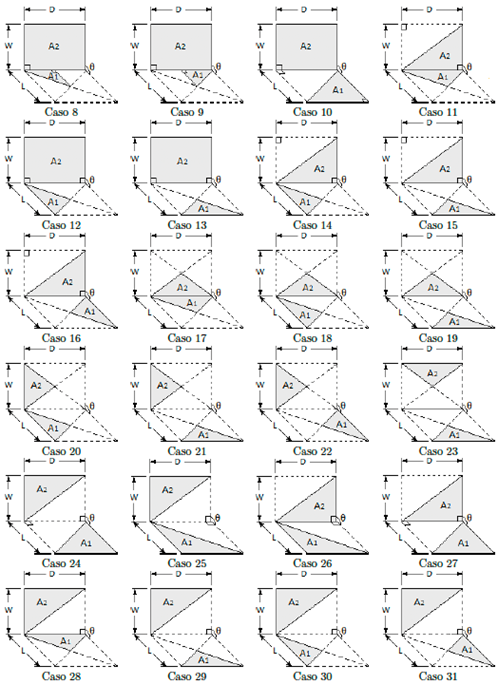
Otras configuraciones geométricas
En la Figura 3, las superficies emisora y receptora son divididas en cuatro superficies triangulares, entonces son posibles 0.5nn−1 = 0.5 · 44−1 = 32 combinaciones (véase la Figura 11). Mediante los factores de visión f(1) al f(8) es posible obtener los factores de visión para las restantes configuraciones, aplicando la regla de sumas y el álgebra de factores de forma. En la Tabla 5 son resumidas las relaciones para computar el factor de visión en las configuraciones dadas en la Figura 11.
Conclusiones
Fue desarrollado un método aproximado para la determinación del factor de visión en 32 combinaciones de geometrías triangulares con bordes comunes y ángulo θ incluido, situadas en un espacio 3-D.
Para la validación de los modelos propuestos fueron evaluados 42 ejemplos con varias relaciones de aspecto para cada geometría de los ocho casos básicos, comparando los resultados obtenidos mediante la SA, con los arrojados por la RMS con cinco intervalos y los computados por el método propuesto con RCB.
En todos los casos evaluados, la RCB mostró los mejores ajustes, con un error de ±6 % en más del 90 % de las muestras, mientras que la RMS mostró una dispersión media de ±6 % en el 65 % de los datos. Este elemento confirma la validez de la hipótesis sobre su uso. Para las restantes 24 configuraciones geométricas estudiadas fueron presentadas las relaciones básicas para el cálculo del factor de visión a partir las expresiones obtenidas para los ocho casos básicos La naturaleza práctica de la contribución y los valores razonables de ajustes obtenidos, permiten considerar a la propuesta como una herramienta adecuada para su uso en la ingeniería térmica y en las tareas de cálculo de la transferencia de calor por radiación.
Dada la ausencia de antecedentes similares en la literatura, el método propuesto refuerza el valor científico y práctico de esta investigación, pudiendo ser incorporadas las soluciones proporcionadas a los catálogos disponibles en la actualidad, para el cálculo de los factores de visión.