1. INTRODUCTION
Over the last decade, Interconnection and Damping Assignment Passivity-Based Control (IDA-PBC) has experienced increasing practice due its wide applicability (Petrovi´c et al., 2001; Batlle et al., 2004, 2007; Ortega and García-Canseco, 2004; Li et al., 2010; Astolfi and Ortega, 2001; Fujimoto et al., 2001; Renton et al., 2012; Li et al., 2013; Astolfi et al., 2002a; Xue and Zhiyong, 2017). The standard IDA-PBC method requires a two step procedure: energy shaping and damping injection. The first depends on the solution of partial differential equations (PDEs) and the second together with zero state detectability (ZSD) of the closed-loop guarantees asymptotic stability.
In order to simplify the PDE problem Viola et al. (2007) have introduced a change of coordinates and a modification of the target dynamics. With the objective to completely avoid PDEs, the following leading methods have been proposed: constructive procedures (Donaire et al., 2016a; Borja et al., 2016; Romero et al., 2017), implicit port-Hamiltonian representation (Macchelli, 2014; Castaños and Gromov, 2016) and an algebraic approach (Fujimoto and Sugie, 2001; Batlle et al., 2007; Nunna et al., 2015). In addition, it has been shown in (Batlle et al., 2007; Donaire et al., 2016b) that a two step IDA-PBC may be restrictive in some cases, thus introducing a single step procedure (SIDAPBC). Furthermore, dissipation in the under-actuated degrees of freedom, see (Gómez-Estern and Van der Schaft, 2004), may also turn out an obstacle for the implementation of IDA-PBC on some systems, e.g. on the cart-pole system (Delgado and Kotyczka, 2014).
It is well-known that actuator saturation (AS) can cause performance losses or even lead to closed-loop instability. In this context, Åström et al. (2008); Escobar et al. (1999) have studied PBC with AS on two specific systems. Sun et al. (2009); Wei and Yuzhen (2010) analyze stability for saturation in the damping injection term. A variable structure approach to energy shaping for a class of Port-Hamiltonians system is developed in (Macchelli, 2002; Macchelli et al., 2003). Besides, Sprangers et al. (2015) studied a reinforcement learning method for energy shaping which shows robust properties under AS.
In polynomial systems the sum of squares (SOS) approach with semidefinite programming (SDP) allows to synthesize Lyapunov functions (Parrilo, 2000), optimal (Ichihara, 2009), robust (Zhu et al., 2018; Jennawasin et al., 2010), fuzzy (Wibowo et al., 2014; Yu and Wang, 2013) and AS-focused controllers (Jennawasin et al., 2012; Valmorbida et al., 2013; Ichihara, 2013), among others. This AS controllers, calculated with SOS, use the polytope representation introduced in (Hu and Lin, 2001) for linear system with multiple input saturation.
For a class of polynomial affine systems, lately, Cieza and Reger (2018) have presented an algebraic method the conditions of which are met by means of SOS and SDP solutions. The method solves the typical problems of IDA-PBC at the expense of an adequate parametrization and selection of the Hamiltonian. To the best knowledge of the authors there is no definitive solution to the AS controller design problem with IDA-PBC. The underlying work shall now also incorporate AS and two minimization objectives in the SDP solver, extending the algorithm of Cieza and Reger (2018).
The work is organized as follows. We summarize the concepts of IDA-PBC for nonlinear affine systems in Section 2. Section 3 recapitulates the algebraic method of Cieza and Reger (2018). In Section 4 we solve the AS problem in the algebraic approach using additionally two minimization objectives. We discuss the application of SOS methodology and verify our results in Section 5, applying the approach on two polynomial systems. Finally, we draw our conclusions in Section 6.
2. IDA-PBC FOR AFFINE NONLINEAR SYSTEMS
Let us recall the IDA-PBC approach for nonlinear affine systems introduced by Ortega and García-Canseco (2004). Consider the system
and the target port-Hamiltonian system
where
is fulfilled for some
transforms (1) into the stable system (2) with Lyapunov function Hd. Asymptotic stability of
3. IDA-PBC FOR POLYNOMIAL SYSTEMS
In this section we summarize Proposition 4–5 from (Cieza and Reger, 2018) for
3.1 Algebraic IDA-PBC
Let
and the desired closed loop port-Hamiltonian system
where
Without loss of generality let
Proposition 1 Closing the loop of system (4) with control
renders the equilibrium point
C1 There exist polynomial functions
C2 There is a polynomial function
C3 There is a constant matrix P, and polynomial matrices
Furthermore, the origin of (5) is asymptotically stable if
for
Proof 1 It can be found in (Cieza and Reger, 2018) with a modification of (8) using the Schur complement.
3.2 Existence of ub
The next proposition provides a sufficient condition for the existence of F2, i.e. the existence of the (asymptotically) stabilizing control law (6).
Proposition 2 Consider
with
Lastly, if (10) or (11) are satisfied, then a solution for F2 with
Proof 2 See (Cieza and Reger, 2018, Prop. 5).
Application of the algorithm starts with adequate selection of
In comparison, Proposition 2 requires the solution of smaller LMIs to calculate the parametrized function F2, see (12), or to guarantee its existence, whereas Prop. 1 defines F2 as general function s.t. (7) (and (9)) is satisfied, which grants more flexibility at the expense of computational cost. In order to use SOS with SDP we force F2 (in Prop. 1) to be a polynomial function of some selected degree.
Proposition 2 can also be used as a fast indicator such that Proposition 1 will work. Note that Proposition 2 contains the minimal conditions that
4. MAIN RESULTL
In view of Proposition 1 and 2, we extend the results of Cieza and Reger (2018) to consider actuator saturation (AS). In addition, we define two possible minimizations (optimization objectives) for the SDP.
4.1 Actuator Saturation (AS)
Proposition 3 Let all conditions of Prop. 1 for local (asymptotic) stability be satisfied and assume:
C5 There exist polynomial matrices
Then the stabilizing control law (6) is restricted to
Proof 3 Multiplying (14) on both sides by adequate matrices and using the Schur complement yields
where last equalities are obtained with (13) and (6).
After solving the conditions of Proposition 1 and 3, we may calculate a control input
and on the left by its transpose. This results in conditions that can be solved by means of SOS + SDP
Following the works of Hu and Lin (2001); Valmorbida et al. (2013); Ichihara (2013), among others, we may use the polytope or polytopic saturation model within the algebraic IDA-PBC, as phrased in the following proposition.
Proposition 4 Let the conditions of Propositions 1 and 3 be satisfied for some system of the form (4) resulting in some matrices P, F2 and a locally (asymptotically) stabilizing constrained controller
provided that there exist matrices
Proof 4 Define
and rewritten as a sum of positive semidefinite polynomial functions (convex set) this yields
Proposition 4 implies that if there is a solution to the conditions of Propositions 1 and 3 with (17), then there also exists an (asymptotically) stabilizing control law (16). In addition, if
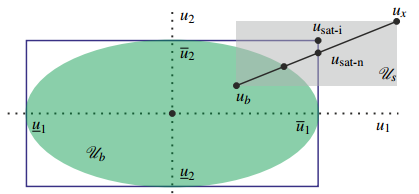
In the same way as in (Hu and Lin, 2001; Valmorbida et al., 2013; Ichihara, 2013) for multiple input systems, we can adopt the independent input saturation given by
Here, we also observed that in order to have AS, independent input saturation (usat-i) is not the only solution. Therefore, to simplify (17), we select
which is also shown in Figure 1. Selection of
4.2 Optimization Objectives in SDP
Proposition 1–3 only guarantee a solution for P and F2(x) without any performance or optimization goal in the SDP. In addition, we may set the following simple objectives:
Optimization 1 (Volume maximization of XP)
Proof 5 The volume of XP is proportional to
for any real matrix
This minimization is also used empirically in (Ichihara, 2013). Optimization 1 maximizes the volume of XP by maximizing the minimum bound of P given by Y-1. Note that searching for the biggest XP does not demand the explicit selection of x0 (right hand side of (8)).
Optimization 2 (Volume minimization of Ub)
Proof 6 Along the same lines of Optimization 1, except that we consider the upper bound of (21).
Without loss of generality, define
for all
5. SIMULATIONS
It is well-known that the SOS property is a sufficient condition for checking the non-negativity of a polynomial function (Parrilo, 2000). For this reason, we may search for positive semidefinite matrices that are matrix SOS polynomials in Propositions 1–4. To guarantee strict inequalities in the SDP solver, we add
In the following examples we search for asymptotically stabilizing controllers wrt. two systems using the results of Proposition 1–4. Values presented in this paper have been rounded to three decimals for better visibility.
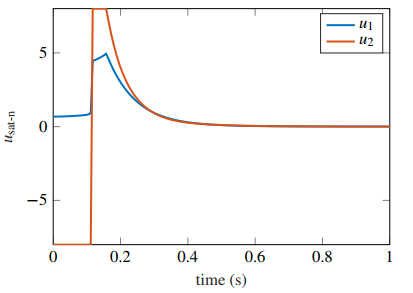
5.1 Nonlinear Second Order System
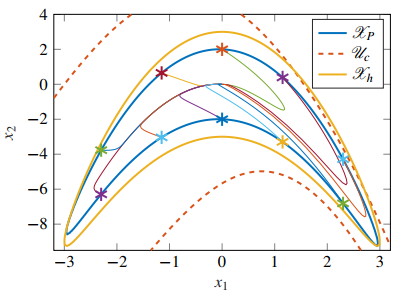
We shall test Proposition 1–3 for synthesizing an asymptotically stabilizing constrained controller in the system
First, we pick
Next, for illustration we select (a minimum bound on P)
Finally, we evaluate Prop. 1 and 3 with Opt. 1 selecting, for instance,
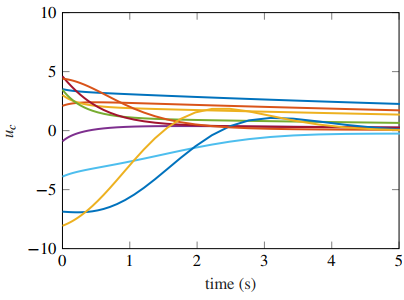
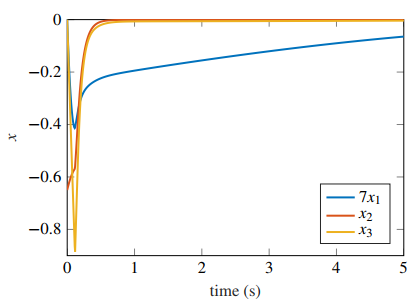
5.2 Third Order Multiple Input System with AS
Now, we consider a third order system given by
with AS using
and
6. CONCLUSION
In this paper we provide an algebraic solution for IDA-PBC that is able to resolve the problem of actuator saturation. To this end, we restrict the design to a class of polynomial systems that yield conditions which are solvable with SOS and SDP. The presented algorithm requires the following steps:
Additionally, we enjoy features as: no need to solve a PDE, dissipation in design, and one step IDA-PBC. Simulations of two polynomial example systems validate our approach.