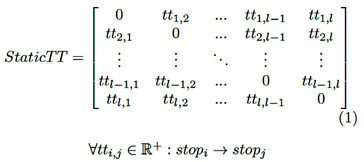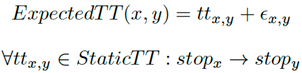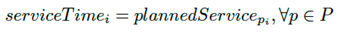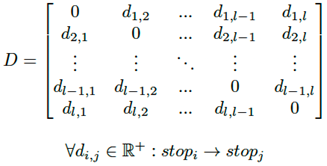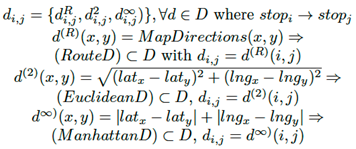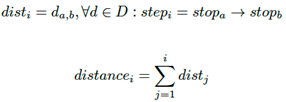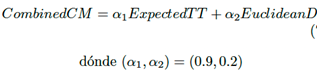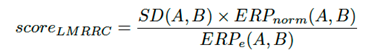Introducción
La definición adecuada y la secuenciación de múltiples paradas en rutas de carga tienen un impacto práctico directo en la eficacia de los transportes, la logística y el consumo de combustible [1]. Estos factores fomentan la búsqueda de soluciones eficientes en tiempo y óptimas, capaces de desempeñarse de manera aceptable en casos de uso reales y escalables en las crecientes demandas diarias de entregas [2]. Esta sección incluye información relacionada con la génesis del proyecto en el contexto de un concurso reciente de Amazon y el MIT, y continúa definiendo los principales problemas subdivididos tanto en aprendizaje supervisado como en aprendizaje no supervisado, como se tratan en este documento; finalmente, una vez que se consideran estos temas, se propone un flujo temático consecuente, especificando las bases y las contribuciones originales de este trabajo.
Reto de investigación en ruteo de última milla de Amazon, con el apoyo del MIT
Durante el período de marzo a junio de 2021, tuvo lugar la competición conocida como LMRRC [3], que promovió a los participantes a agruparse y resolver un problema de optimización de ruteo de carga terrestre con datos reales de rutas en ciudades de los Estados Unidos con una gran demanda de entregas de última milla (es decir, transporte desde el depósito inicial o la estación hasta varios sitios de entrega), buscando soluciones originales e innovadoras para la secuenciación de nodos geográficos. Estos datos correspondían a información sobre paradas, paquetes y tiempos de viaje para cada una de las 6,125 rutas de entrenamiento y validación cuya segmentación ya estaba definida. En total, había 1.457,175 paquetes y 898,415 paradas, donde varios paquetes estaban vinculados a cada parada, que a su vez estaban asociados a un identificador de zona específico de la ciudad. Cada una de estas rutas también tenía una secuencia real con la cual comparar los resultados según un puntaje de "diferencial de pedido" que se hacía más pequeño cuanto mejor desempeñaran los algoritmos; posteriormente, se generalizó en el conjunto de pruebas. El equipo de los autores, llamado AlphaCentauri, se clasificó como uno de los equipos con mejor desempeño en la competición.
Declaración del problema
Con un enfoque en la expansión de la iniciativa LMRRC, las dificultades globales abarcan desde ciertos aspectos del aprendizaje supervisado a través de algoritmos de predicción y ruteo, con el objetivo de alcanzar los mejores resultados posibles con respecto a soluciones predefinidas.
El problema actual de ruteo de carga requiere aproximar una secuencia de paradas basada en el diagrama de solución proporcionado por conductores experimentados, teniendo en cuenta el conocimiento previo sobre transportes de paquetes anteriores y el estado de las rutas. Todos los paquetes carecen de peso, pero tienen dimensiones, al igual que las unidades de transporte individuales por ruta, lo que puede requerir la necesidad de reabastecimiento en la estación. Además, algunos paquetes están sujetos a ventanas de tiempo bastante flexibles que limitan las horas de provisión de los paquetes. La mayoría de las paradas están vinculadas a zonas geográficamente distribuidas, con dependencias variables 1: ni para paquetes y paradas, así como paradas y zonas. Se conocen todas las combinaciones posibles de tiempos de viaje entre las paradas, además de sus coordenadas y el tiempo de servicio planificado necesario para cada paquete. La situación se plantea como un tipo de problema del viajante asimétrico sin regreso o un problema del camino hamiltoniano ponderado con ventanas de tiempo y restricciones de capacidad.
Este artículo sigue una disposición lógica con el fin de abordar todo el proceso de preparación de datos, organización de estructuras, experimentación con algoritmos y observación de resultados.
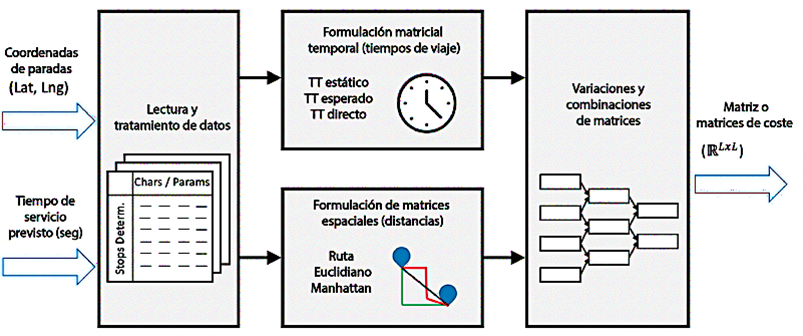
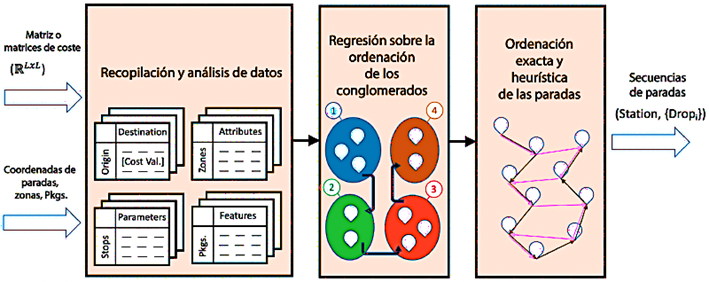
La Figura 1 muestra la secuencia temática propuesta a nivel global. Este trabajo se centrará principalmente en las formulaciones de matrices de costos personalizadas y en el enrutamiento adaptativo de paradas a través de rutas extremadamente diversas, al mismo tiempo que examinará las principales aplicaciones, limitaciones y errores de las metodologías.
Revisión de la literatura
Los problemas de optimización de clustering y ruteo a gran escala en logística han sido temas de investigación desde mediados del siglo XX, incluso antes de que se establecieran los términos y prácticas de aprendizaje no supervisado y supervisado, y las aplicaciones contemporáneas se hicieran populares. Varias investigaciones [4] buscaron utilizar el clustering, entre otras técnicas, para programación de producción y estimaciones óptimas de movilización, mientras que [5] sigue siendo uno de los primeros registros de aproximaciones a soluciones para problemas de ruteo a gran escala. En esta sección se mencionan generalidades de investigaciones recientes sobre estos temas, centrándose en contenidos relacionados con la investigación actual.
Investigación sobre el ruteo de carga
El caso general del ruteo de carga implica la búsqueda de la secuencia óptima de nodos (conocidos como paradas) en un conjunto de rutas para una flota de vehículos que debe satisfacer algunas demandas de los clientes, como el estado de las carreteras, la capacidad de carga de los vehículos, los tiempos de viaje entre cada parada, los tiempos de procesamiento por paquete entregado, las ventanas de tiempo en las que algunos paquetes deben ser despachados y las horas de trabajo de los conductores. En las siguientes subsecciones, se realiza una revisión de los enfoques de ruteo habituales y se presenta una exposición a través de ejemplos de temas recientes de investigación en ruteo.
Resumen de enfoques de ruteo
Ciertas optimizaciones de ruteo de carga son problemas NP-duros [6] que implican la secuenciación de paradas para cumplir con las restricciones de una unidad física que transporta paquetes con dimensiones y peso [7].
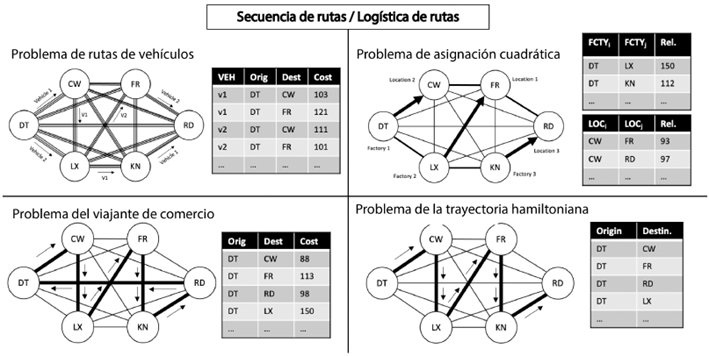
La formulación inicial del problema puede variar, considerando la posibilidad de volver a la parada inicial y el uso de una o varias unidades de transporte. La Figura 2 ilustra problemas típicamente interrelacionados, incluyendo el problema del ruteo de vehículos (VRP) [8], que es NP-completo y NP-duro y busca rutas de longitud mínima y tiempo mínimo para una flota. El problema de asignación cuadrática (QAP) [9], asigna instalaciones a diferentes ubicaciones para minimizar distancias multiplicadas por flujos. El problema del viajante de comercio (TSP) [10], busca la secuencia más corta, visitando cada parada exactamente una vez antes de regresar a la estación inicial. Este problema tiene aplicaciones en logística, fabricación de microchips [11] y secuenciación de ADN [12]. El problema del camino hamiltoniano (HPP) [13], un subproblema de TSP, busca una secuencia global óptima sin volver a la estación, apuntando a un grafo hamiltoniano conectado con rutas únicas entre todos los vértices. La búsqueda exhaustiva no es factible debido al número de ciclos hamiltonianos diferentes: (n−1) 2 en un grafo completo no dirigido con n paradas y (n − 1)! en un grafo completo dirigido.
Aplicaciones de ruteo relacionadas
A nivel global, los escenarios de ruteo tienden a buscar procedimientos innovadores y particulares a través de algoritmos eficientes en tiempo que faciliten los esfuerzos de las empresas para brindar un servicio efectivo y reducir los costos de transporte. Esto se puede observar en documentos como [14], que utiliza enfoques recientes de computación cuántica para VRP, utilizando cuantificadores y simuladores de enfriamiento. De manera similar, las posibles resoluciones del QAP se analizan en [15-17], utilizando formulaciones de QUBO e Ising. En cualquier caso, aunque la naturaleza de los problemas sea específica, la búsqueda de protocolos de optimización de ruteo de uso general para el transporte aéreo, marítimo y terrestre sigue siendo un área de investigación activa [18, 19].
En cuanto al problema del viajante de comercio (TSP), se han desarrollado múltiples enfoques, incluyendo algoritmos lógicos estándar como el algoritmo voraz (por ejemplo, el vecino más cercano) y/o con programación dinámica, así como aproximaciones basadas en heurísticas constructivas como el multifragmento [20] y diferentes técnicas de optimización de variables [21]. Sin embargo, ninguna de estas posibilidades alcanza una solución global en tiempo polinómico y se consideran inaplicables al problema actual, dada la gran cantidad de paradas en cada ruta y sus interrelaciones.
En relación con el problema de ruteo específico, las Actas Técnicas del MIT LMRRC ilustran las propuestas de varios competidores que enfrentaron el desafío desde una amplia gama de perspectivas. Al analizar los documentos y algoritmos de los finalistas, CHH [22] sugiere realizar búsquedas locales por tiempo de viaje en las que se aplican restricciones de precedencia, camino y vecinos para secuenciar áreas aprendidas basadas en penalizaciones. Luego, GMW [23] presenta un enfoque no entrenado por zonas en tres niveles, junto con una modificación lineal de la matriz de costos de tiempos de viaje y una etapa posterior de posprocesamiento de la secuencia final para posibles inversiones de secuencia. De manera similar, ArsAb [24] aporta un procedimiento voraz junto con un algoritmo genético previamente entrenado con una subrutina de TSP también basada en penalizaciones. Finalmente, HSFv1 [25] propone una combinación de enfoques exactos y heurísticos que concilia múltiples perspectivas posibles y se generaliza adecuadamente para el conjunto de pruebas del LMRRC (mejorando así la puntuación resultante en relación con las rutas de validación).
Investigación sobre multimetodologías
Las multimetodologías para la logística de ruteo han evolucionado con el tiempo para abordar los desafíos complejos asociados con la optimización de rutas de transporte, al mismo tiempo que mejoran el comercio electrónico [26] y los enfoques colaborativos [27] con el fin de aumentar la eficiencia y reducir los costos de entrega. Estudios recientes relacionados [28, 29] sugieren diversos métodos jerárquicos multietapa para resolver el problema de ruteo de vehículos para una flota heterogénea con varias restricciones; su característica única es la proximidad a la práctica logística real. Otras propuestas [30, 31] ayudan a reducir el desperdicio después de la cosecha durante el proceso de recolección mediante el uso de flotas internas y contratadas con capacidades heterogéneas, y empleando un heurístico basado en algoritmos voraces y varios métodos de búsqueda local para obtener soluciones cercanas a lo óptimo.
Además de las interesantes metodologías simultáneas para la recogida y entrega en las cadenas de suministro para el comercio electrónico [32] cuando se entrenan con una gran cantidad de rutas [33], ha habido una demanda creciente de enfoques mixtos eficientes en el mundo real debido a la reciente epidemia de COVID-19 [34]. Los resultados experimentales proporcionados enriquecen la investigación relacionada con modelos y algoritmos de problemas de ruta de vehículos en grandes emergencias de salud pública y brindan soluciones optimizadas para la distribución de ayuda a los tomadores de decisiones de logística de emergencia [35]. Trabajos similares [36] investigan un problema de ruteo colaborativo de camiones y drones para la entrega de paquetes sin contacto en áreas epidémicas, que combina el criterio de aceptación de Metrópolis [37] de Simulated Annealing y Tabu Search para la logística urbana en ciudades inteligentes [38].
Materiales y métodos
Formulación de matrices de costo
Definir las matrices de costo es crucial para los procedimientos de secuenciación, lo que permite la estructuración y resolución del problema. Incluso pequeñas variaciones en estas matrices pueden provocar cambios significativos en los resultados de la optimización de ruteo. La Figura 3 ilustra dos enfoques para definir las matrices de costo, cada uno con sus propias variaciones para la combinación y ajuste de parámetros.
Información temporal a través de tiempos de viaje
Los datos relacionados con el tiempo, utilizados como matriz de costos, son útiles para enfoques abstractos independientes de la distancia. El parámetro tradicional para escenarios de ruteo generales es utilizar una matriz de tiempos de viaje asimétrica cuadrada en la que cada elemento contiene el valor en segundos necesario para el movimiento unidireccional de una parada a otra. Para un conjunto dado de l paradas, se define una matriz temporal general de acuerdo con la Ecuación (1).
(1)
Esta expresión se conoce como la matriz de tiempos de viaje estática, donde se tienen en cuenta las características típicas del transporte (por ejemplo, velocidad del vehículo, aceleración).
Una alternativa relevante consiste en la matriz de tiempos de viaje esperados (Ecuación (2)), donde a cada elemento se le asocia una perturbación individual, ya que se informan las propiedades de tránsito para un momento y fecha específicos (por ejemplo, embotellamientos, falta de señalización).
(2)
Por lo tanto, definiendo P como el conjunto de paquetes asociados a una ruta dada, la traza de tiempo actual (Ecuación (3)) contada para un intervalo de secuencia i se calcula como la suma del tiempo de inicio de la ruta con el tiempo de servicio planificado por paquete y la duración de los tiempos de viaje hasta ese punto.
(3a)
(3b)
(3c)
Las consideraciones de tiempo son importantes para los tiempos de viaje, incluyendo ventanas de tiempo, restricciones y restricciones específicas de paquetes. Enfoques más simples utilizan una velocidad de vehículo constante, mientras que opciones más complejas consideran velocidades distribuidas basadas en configuraciones de calles.
Información espacial a través de distancias
Los datos basados en la distancia utilizados como matriz de costos son ventajosos para perspectivas geográficas independientes del tiempo. De manera similar al caso anterior temporal, la instancia general representa una matriz cuadrada principalmente asimétrica con valores de distancia que vinculan unidireccionalmente una parada con otra. De manera análoga a la expresión dependiente del tiempo, se examinan todas las combinaciones posibles, como se muestra en la Ecuación (4).
(4)
El elemento de distancia mencionado se considera indirecto (es decir, distancias de rutas, donde se respetan las direcciones de las calles y las siluetas) o directo (por ejemplo, distancias euclidianas o de Manhattan, donde no se requieren exámenes relacionados con las calles). Las formulaciones concernientes con estas distancias son:
Luego, la traza de distancia actual (Ecuación (5)) con respecto a un intervalo de secuencia i se calcula como la suma de todas las distancias anteriores siguiendo el orden de las paradas.
(5)
En contraste con el cálculo de tiempo actual, la expresión de distancia actual es computacionalmente más fácil de gestionar y depende de menos parámetros una vez que se determina la matriz de costo espacial.
Información mixta a través de combinaciones de matrices
Las variaciones de matrices en los costos de tiempo y espacio ofrecen una perspectiva diferente del problema, considerando atributos aparentemente independientes.
Sin embargo, es necesario examinar y ajustar combinaciones de parámetros estándar para lograr simplicidad y generalidad.
La formulación de la matriz de información mixta (CCM) se expresa en la Ecuación (6), considerando las matrices temporales y espaciales. Observaciones empíricas muestran la similitud y redundancia de StaticTT y ExpectedTT para trayectorias de última milla. DirectTT se considera demasiado general e impreciso, mientras que la matriz de costos RouteD varía según las coordenadas y las actualizaciones del transporte local.
(6)
Algoritmos de secuenciación de rutas
La planificación de rutas es vital para la secuenciación eficiente del transporte, determinando el orden de las paradas para optimizar la entrega. La propuesta de LMRRC considera diversos factores, como variaciones de tiempo, algoritmos basados en métricas y distancias, y alternativas simétricas/asimétricas [39]. Para abordar el desafío de múltiples perspectivas, se propone un enfoque múltiple que combina metodologías de aprendizaje, exactas y heurísticas.
La Figura 4 representa el flujo de procedimientos, que incluye la generación de secuencia de paradas, la determinación de atributos y matrices de costos. La sección global analiza las características de las rutas, utiliza la regresión para la ordenación de los clústeres y presenta enfoques exactos/heurísticos para las paradas individuales. Los resultados de validación se comparan utilizando una puntuación de variación. Este desafío de secuenciación fue central en la competición LMRRC.
Análisis general
La metodología propuesta adopta un proceso sistemático que incorpora enfoques de regresión, exactos y heurísticos para proporcionar una solución directa y completa. Los enfoques de regresión utilizan algoritmos de aprendizaje específicos y experimentación pasada para hacer predicciones. Sin embargo, depender únicamente de la regresión puede llevar a predicciones demasiado dependientes de los datos de entrenamiento, especialmente al considerar múltiples ciudades y contextos. Los enfoques exactos buscan encontrar soluciones precisas para problemas con restricciones, pero pueden ser computacionalmente intensivos en escenarios prácticos. Por otro lado, los enfoques heurísticos ofrecen soluciones aproximadas en plazos razonables, aunque con una precisión reducida. El procedimiento propuesto combina estratégicamente estos enfoques para maximizar su utilidad.
La Figura 5 ilustra el procedimiento general que abarca todos los enfoques considerados, garantizando resultados relevantes dentro de un marco de tiempo realista. La naturaleza no iterativa de la metodología facilita una ejecución eficiente. Además, para mejorar el análisis inicial y facilitar la comparación de los resultados finales, se estudian ciertas características de las rutas de interés como parte del paso de extracción de características:
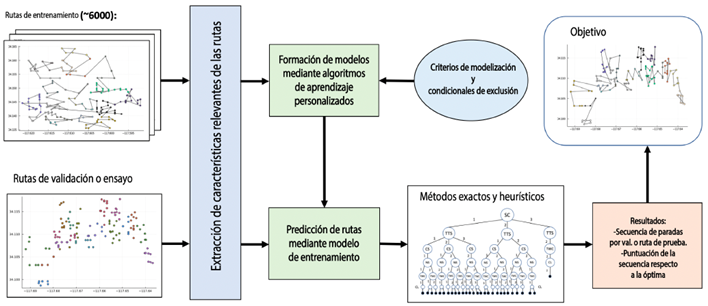
Figura 5 Proceso general de ruteo que incluye una fase de aprendizaje, así como enfoques exactos y heurísticos.
Ratio de extensión de ruta (RER): Relación espacial por ruta, considerando todo su conjunto de zonas.
Ratio de extensión de zona (ZER): Relación espacial por zona, considerando todo su conjunto de paradas.
Variación de extensión de zona (ZEV): Diferencia entre las dimensiones espaciales máximas y mínimas de las zonas incluidas en la ruta (promediando en longitud y latitud).
Cantidad de paradas por zona (SAZ): Cantidad de paradas en una zona dada a partir de los datos de una ruta.
Variación de paradas por zona (SVZ): Diferencia entre la cantidad máxima y mínima de paradas del conjunto total de zonas pertenecientes a la ruta de interés.
Cantidad de zonas por ruta (ZAR): Cantidad de zonas en una ruta dada.
El paso de aprendizaje estima la secuencia de zonas utilizando los datos de entrenamiento del LMRRC y la observación de que generalmente se conserva el orden de los clústeres independientemente de la ciudad, con el objetivo de minimizar la variación entre grupos de paradas contiguas. Sin embargo, para tener en cuenta los casos en los que las secuencias de clústeres aprendidas no se continúan fielmente en rutas posteriores, se definen condicionales de exclusión. A continuación, se emplean perspectivas globales exactas y heurísticas con parámetros específicos para completar el orden de clústeres no cubierto por el paso de aprendizaje y organizar las paradas restantes.
Metodología de aprendizaje
La regresión presentada busca encontrar relaciones entre clústeres de paradas contiguas, basándose en la hipótesis de que la secuencia de zonas previamente aprendida se mantiene en su mayoría y se repite en rutas posteriores. Los clústeres se dividen en cuatro capas y se identifican con caracteres alfanuméricos con una distribución espacial heterogénea y siluetas dinámicas. Esta necesidad de una metodología de aprendizaje se basa en la visualización de rutas y el examen de secuencias históricas, determinando así una correlación y dependencia hacia secuencias de paradas inicialmente independientes que se derivan de las consistencias en la definición e identificación de clústeres.
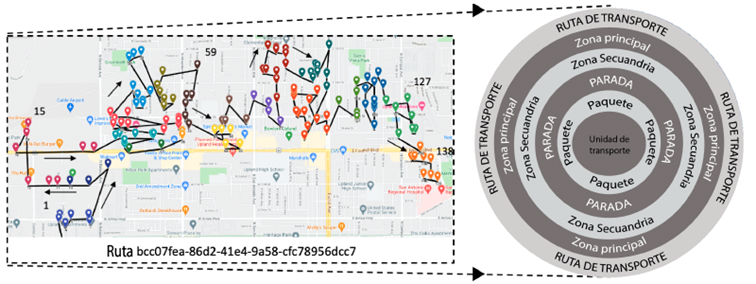
Motivación empírica
Las secuencias de paradas observadas siguen un patrón de visitar todas las paradas dentro de una zona antes de avanzar, priorizando clústeres contiguos y teniendo en cuenta la estructura de zonas y paquetes. Esto sugiere un enfoque de capas, simplificando el enrutamiento con un promedio de ocho paradas por clúster y enfatizando la secuenciación precisa de zonas. La Figura 6 ilustra esta perspectiva de capas, completando las paradas dentro de las zonas antes de avanzar, independientemente de la proximidad. El enfoque de aprendizaje se centra en las zonas principales y secundarias, buscando la simplicidad y resultados variables, ya que las capas principales permanecen estables dentro de una ruta.
Algoritmo para el orden de clústeres
El paso de entrenamiento del algoritmo de regresión construye un modelo a partir de un conjunto de datos de entrenamiento, contando las repeticiones de secuencias de clústeres para zonas principales y secundarias de forma independiente, agrupadas en conjuntos de 7. Las zonas principales y secundarias consisten en capas alfabéticas y numéricas, siendo la capa numérica la más variable (por ejemplo, rangos de caracteres ‘A-F’ y ’1-25’). Las condiciones de exclusión relevantes incluyen diferencias en las primeras capas de las zonas principales (es decir, dif (M1 (j), M1 (j+1)) ≥ 1), una diferencia de tres o más puntos en la primera capa de las zonas secundarias (es decir, dif (m(j) 1, m(j+1) 1) ≥ 3) y una variación de Unicode de seis o más puntos en todas las capas de zonas (es decir, ∑i dif(z(j) i, z(j+1) i) ≥ 6). La profundidad del modelo es más superficial para las zonas principales, pero se vuelve más específica para las zonas secundarias. Dado la repetibilidad constante de los identificadores y un promedio de 21 clústeres por ruta, el algoritmo de entrenamiento tiene una complejidad de O(m) para rutas con m zonas y tarda aproximadamente 0,15 segundos en un procesador Quad-Core i7 de 2.3 GHz.
En el paso de evaluación, las zonas se ordenan inicialmente utilizando las secuencias del modelo con las repeticiones más altas. Los clústeres no utilizados se verifican en secuencias con repeticiones progresivamente más bajas y se incorporan en el orden inicial si se encuentran. Si quedan zonas no utilizadas, se ordenan utilizando diseños exactos y aproximados, como se explica en la siguiente sección. Este proceso también tiene una complejidad de O(m) y lleva alrededor de 0,4 segundos por ruta.
Enfoques exactos y aproximados
Para determinar la secuencia de paradas de cada clúster y considerar valores atípicos y particularidades del paso de aprendizaje previo, se definen un conjunto de reglas y posibilidades exactas y heurísticas. Los enfoques sugeridos, realizados empíricamente a través de la observación y la determinación de parámetros, buscan proporcionar soluciones con complejidades de tiempo realistas que se aproximen a los resultados óptimos dados.
Diseño del procedimiento
El proceso de definición de reglas comienza por comprender el problema y clasificar cada ruta de entrada en función de las características RER, ZER, SAZ y ZAR. Luego se determinan los atributos relevantes, formando una jerarquía que refleja las decisiones tomadas por secuencias reales. Los enfoques y configuraciones definidos se prueban utilizando un procedimiento de programación con nuevas rutas. Finalmente, los resultados obtenidos de estas formulaciones y ejecuciones se comparan para optimizar la salida.
La Figura 7 describe las pautas cronológicas para definir y probar parámetros exactos y heurísticos. La programación involucra tres pasos basados en las jerarquías de atributos mencionadas anteriormente. El enfoque de capacidad tiene la menor influencia en la estructuración general de la ruta, lo que hace que variables como las dimensiones de los paquetes sean auxiliares. El enfoque temporal, que implica cálculos basados en el tiempo actual y las especificaciones de ventanas de tiempo, también se considera secundario en comparación con las características típicas de la ruta global.
Definición de parámetros
Los siguientes atributos son considerados útiles para la designación de rutas, centrándose en casos y enfoques empíricamente relevantes:
Secuenciación de clústeres (CS): Orden de las zonas que quedan sin usar en el enfoque de aprendizaje.
Distancia métrica (CS1): Separación euclidiana mínima exacta desde los baricentros de zonas contiguas, determinados como el punto medio geográfico de cada polígono de clúster.
Distancia de conjunto (CS2):I ntervalo de Hausdorff mínimo heurístico entre zonas contiguas.
Orden de paradas (SO): Secuencia de paradas dentro de un clúster dado.
Enfoque global (SO1): Búsqueda exhaustiva o reducida exacta del costo mínimo global.
Enfoque local (SO2): Búsqueda heurística del costo mínimo local en paradas contiguas.
Definición de paradas de transición (TSD): Determinación de paradas entre clústeres.
Última parada interna (TSD1): La última parada del clúster actual es la primera parada del clúster siguiente.
Primera parada externa (TSD2): Enfoque local entre clústeres para la primera parada del clúster siguiente.
Condiciones de ventana de tiempo (TWC): Impulso o retraso de paradas en la secuencia basado en la hora de ocurrencia.
Perspectiva de clúster (TWC1): Modificación del orden, basada en ventanas de tiempo exactas por clúster.
Perspectiva de ruta (TWC2): Modificación del orden, basada en ventanas de tiempo globales heurísticas.
Limitaciones de capacidad (CL): Necesidad de reabastecer el transporte en el depósito según el exceso de carga.
En la división de clústeres (CL1): Reabastecer antes de entrar en el clúster siguiente, si es necesario.
Saturación máxima (CL2): Reabastecer cuando la unidad alcanza la capacidad máxima local.
La utilización de estas tareas o parámetros no depende de un paso de entrenamiento, ya que cada escenario se evalúa directamente a través de cada examen de ruta. La matriz de costos mencionada para este problema de optimización de rutas se define principalmente como dependiente del tiempo, como en la Ecuación (7).
(7)
La complejidad necesaria para los casos evaluados utilizando estos enfoques consiste en O(n + m) por ruta con n paradas y m clústeres, lo que requiere un promedio de 0.22 segundos por ruta en un procesador Quad-Core i7 de 2.3 GHz.
Resultados y discusión
Examen de la secuencia
Esta sección analiza las secuencias de validación utilizando métodos cualitativos y cuantitativos. LMRRC proporciona una métrica de puntuación para observar los resultados de ordenación, que incluyen la desviación de secuencia (SD) y la distancia de edición con penalización real (ERPe y ERPnorm).
La métrica produce valores positivos, donde puntuaciones más bajas indican una mejor coincidencia de enrutamiento con la secuencia óptima. Una puntuación entre 0.8 y 1.2 representa un orden aleatorio uniforme, y la secuencia debe comenzar en una estación sin repetición. Las puntuaciones por debajo de 0.1 se consideran competitivas según los criterios de LMRRC.
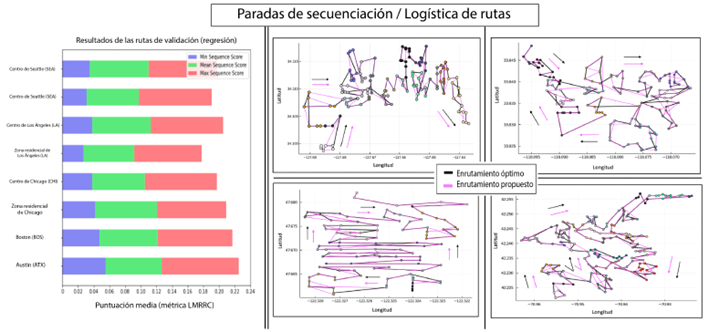
Resultados de validación para la regresión
El ordenamiento de zonas basado en regresión tuvo una variación promedio de puntaje de 0.06 entre la secuenciación correcta e incorrecta de los clústeres. El orden de las zonas principales representó aproximadamente 0.02 de la variación, mientras que el orden de las zonas menores contribuyó a una variación de 0.04 debido a una mayor variabilidad.
La segmentación propuesta en siete clústeres facilitó la identificación de repeticiones coherentes durante la etapa de entrenamiento, sin tener en cuenta las secuencias de transición entre segmentos. Sin embargo, este error de agrupación afectó a menos del 5 % de los escenarios observados, asegurando una gestión eficiente de los datos. El error surgió a partir de una repetición máxima de tres clústeres contiguos por segmento, lo que resultó en un número significativo de clústeres intercalados.
La Figura 8 presenta resultados de ejemplo y secuencias de rutas que ilustran las consideraciones mencionadas anteriormente. La principal causa de error durante la etapa de evaluación fue la verificación secundaria de secuencias del modelo con menos repeticiones y órdenes de clústeres que tenían la misma cantidad de repeticiones. Una mejora podría implicar contar las repeticiones ponderadas basadas en variaciones de Unicode u observaciones empíricas adicionales.
Consideraciones de multimetodologías
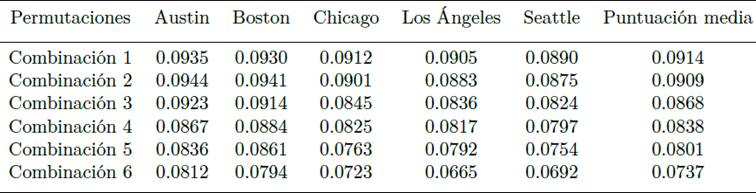
La utilización de métodos metaheurísticos, exactos y heurísticos mejora la precisión del sistema global de paradas enrutadas, especialmente cuando se combinan con el enfoque inicial basado en regresión. Las combinaciones de estos métodos, como se muestra en la Figura 9, se adaptan a diferentes atributos de las rutas. Al modificar los parámetros de enrutamiento, las combinaciones intercambian funcionalidades de análisis global y local, evaluando su impacto en los caminos de validación e identificando las permutaciones más adecuadas.
Los enfoques combinados exactos y heurísticos proporcionan resultados superiores para rutas con un RER y ZAR más altos, especialmente en ciudades como Chicago, Los Ángeles y Seattle. CS2 supera a CS1 con una variación de puntaje de 0.013, como se observa en la Figura 9 y la Tabla 1. SO1 logra el mejor puntaje promedio de aproximadamente 0.006 para SAZ pequeños y ZER más grandes, mientras que TSD1 generalmente supera a TSD2. TWC y CL tienen efectos mínimos, pero TWC1 y CL2 ofrecen ligeras mejoras. CS1 y SO1 son más adecuados para ZEV bajos y SVR altos, mientras que TSD2 y TWC1 también proporcionan mejoras con una variación mínima en el atributo CL.
La Figura 9 ilustra las combinaciones de métodos basadas en las características de las rutas y sus puntajes de validación asociados. La fuente dominante de error es el análisis CS, que impacta significativamente en los resultados. Posibles mejoras implican definir nuevos parámetros y explorar variantes adicionales dentro de los enfoques propuestos.

Figura 9 Resultados promedio y distribuciones de combinaciones particulares de técnicas de enrutamiento de paradas exactas y aproximadas, utilizando atributos característicos de rutas.
Aplicación al caso general
Esta sección analiza los resultados de prueba de todo el proceso, incluyendo las diferenciaciones de paradas, las predicciones de zonas y los mecanismos de enrutamiento personalizado. Las principales observaciones se refieren a las funciones de coste personalizadas y las técnicas de enrutamiento adaptables discutidas en las Secciones 3 y 4. Concluye con observaciones sobre la secuenciación, las aplicaciones de agrupación y generalizaciones a rutas fuera de los Estados Unidos. Estas características de las rutas tienen efectos variables cuando se combinan con algoritmos de optimización derivados de la competición LMRRC.
Características de las rutas
Los conjuntos de datos reales obtenidos constan de 66 rutas de Uruguay, ubicado en la parte oriental del Cono Sur de América. Sus ciudades son considerablemente más pequeñas que las seleccionadas por LMRRC, lo que generalmente se traduce en distancias y tiempos de viaje más cortos entre paradas. También tienen un centro urbano centralizado y densamente poblado donde abundan los negocios, mientras que las calles bidireccionales son escasas. En las zonas periféricas y extendidas se encuentran la mayoría de los mercados y viviendas residenciales. Dado que los transportes viajan diariamente a ambas secciones de la ciudad, sus estaciones permanecen separadas por aproximadamente 20 kilómetros de la parada urbana más cercana. Además, las estructuras de las ciudades no están uniformemente diagramadas, con un promedio global de 85 metros por cuadra y un máximo de 145 metros, lo que también afecta los costos considerados. Finalmente, toda la extensión es bastante plana (sin montañas escalonadas ni valles) y carece de puentes, túneles o metros, lo que complica los tiempos de viaje a larga distancia.
Selección de algoritmos de optimización
La decisión de utilizar cuatro metodologías de enrutamiento se deriva de su clasificación en LMRRC, su disponibilidad y variabilidad, y todas ellas están definidas utilizando los lenguajes de programación Julia y Python [40]. En particular, se utiliza GMW debido a su enfoque y línea de base en los identificadores de zonas y sus relaciones. Luego, se selecciona ArsAb debido a su fase de entrenamiento genético original y mejores resultados en rutas con más de cien paradas. Finalmente, la perspectiva inicial de HSFv1, que declara un procedimiento no entrenado como en el caso de GMW, proporciona mejores resultados en rutas con una relación extrema entre latitud y longitud.
Estos algoritmos se extraen de las Actas Técnicas del LMRRC del MIT [41], que se discuten en la Sección 1.3.3. Además de comparar los resultados de los algoritmos mencionados, la propuesta actual, HSFv2, que incluye una fase de entrenamiento previo y enfoques evaluativos mejorados, se compara con éxito con enfoques más directos que determinan y aprovechan con éxito las características de cada ubicación. De hecho, el procedimiento propuesto se beneficia empíricamente de la diversidad de las multimetodologías seleccionadas y la simplicidad de sus combinaciones. La determinación de paradas y zonas previas se utiliza como pasos preliminares para todos los algoritmos.
Resultados de los algoritmos de optimización
Las rutas seleccionadas tenían extensiones espaciales cuadradas y paradas agrupadas con intersecciones mínimas, lo que facilitó la identificación de zonas y la clasificación de paradas. Un aumento en las paradas por zona llevó a extensiones espaciales no cuadradas, introduciendo una mayor complejidad que favorecía las heurísticas locales sobre los enfoques globales. Varios puntos de conexión tenían identificadores distintos en diferentes análisis de rutas, pero los parámetros ajustados resultaron útiles para nuevas rutas con variación mínima en la puntuación.
La Figura 10 muestra una ruta de prueba con paradas concentradas en áreas del centro y paradas dispersas en otros lugares, donde la predicción de zonas no prioriza las características del clúster.
La Tabla 2 muestra resultados cuantitativos para los cuatro algoritmos de enrutamiento. GMW consistentemente obtuvo mejores métricas con una menor varianza a medida que aumentaba el número de paradas. ArsAb se comportó de manera similar en rutas con muchas paradas. HSFv2 mejoró en comparación con HSFv1, especialmente para longitudes de ruta intermedias. La secuenciación de zonas fue la principal fuente de error, ya que el aprendizaje se basó en rutas de entrenamiento no locales.
Los algoritmos propuestos funcionan y escalan adecuadamente en términos de complejidad temporal y espacial cuando se aplican a rutas de última milla con un máximo de 155 paradas en un procesador Quad-Core i7 de 2.3 GHz, con complejidades comparables o incluso inferiores a las de los algoritmos de la competencia mencionados anteriormente. Esto se considera aceptable, dadas las consideraciones de demanda de las rutas de última milla del mundo real en la actualidad.
Los procedimientos seleccionados también son flexibles para una personalización adicional, al modificar los parámetros de las matrices de coste y al habilitar una combinación diferente de atributos de secuenciación, con el objetivo de admitir múltiples modos de transporte y restricciones. De hecho, filtrar atributos de secuenciación, en particular las consideraciones de CS, permite una disponibilidad más operativa de recursos, lo que se traduce en tiempos de procesamiento más rápidos y una mayor escalabilidad del proceso de secuenciación.
A pesar de las fuentes adicionales de error de paradas personalizadas y predicciones de zonas, las puntuaciones generalmente superaron las secuencias de LMRRC con promedios similares.
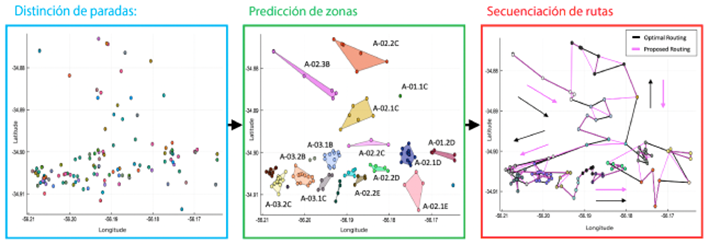
Figura 10 Visualización de los pasos clave del flujo, utilizando una ruta de prueba de ejemplo en Montevideo (Uruguay).
Conclusiones
Esta sección resume y describe los principales logros de este proyecto con un enfoque en la generalización de procesos, incluyendo observaciones sobre posibilidades de investigación futura relacionada y consideraciones destinadas a corroborar y mejorar los resultados obtenidos.
Resumen global
En resumen, este documento proporciona una revisión de componentes importantes del proyecto, seguido de los principios y metodologías clave empleadas. También se discuten las limitaciones y fuentes de error relacionadas con los problemas de interés. La metodología propuesta amplía la iniciativa del concurso LMRRC al secuenciar y planificar rutas geográficamente diversas utilizando registros de GPS en bruto y conjuntos de datos de Estados Unidos y Uruguay. El proceso incluye el filtrado de registros, la predicción de nuevos grupos de paradas y una combinación de enfoques de regresión, exactos y heurísticos para el enrutamiento. La aplicación de este procedimiento a los datos proporcionados arroja puntajes competitivos en rutas de validación (EE. UU.) y demuestra una adaptación y generalización aceptables en rutas de prueba (Uruguay) de LMRRC y OTUC.
Limitaciones relevantes
Los diseños y aplicaciones de modelos de problemas en logística de transporte tienen como objetivo lograr objetivos eficientes. Sin embargo, existen limitaciones prácticas que dificultan su adaptabilidad:
La disponibilidad limitada de rutas y rutas reales de ciudades específicas a nivel internacional, proporcionadas por entidades oficiales, restringe la capacidad de llevar a cabo estudios extensos y completos sobre diversas posibilidades estructurales.
La precisión fija de los datos de coordenadas y numéricos de GPS para la detección de puntos de referencia, así como los valores numéricos relacionados con atributos temporales y espaciales para la formulación de matrices de coste, impone limitaciones a la precisión de los modelos.
Las matrices de coste personalizadas pueden ser
complejas de crear y mantener, especialmente para problemas de enrutamiento grandes y complejos.
La distancia euclidiana no es invariante a escala, lo que significa que multiplicar los datos por un factor común cambiará la distancia. La distancia de Manhattan no tiene en cuenta la curvatura de la Tierra, lo que puede llevar a cálculos de distancia inexactos para distancias largas.
Estimar el tiempo de viaje esperado puede ser difícil de hacer con precisión, especialmente en condiciones de tráfico dinámico.
Un número finito de combinaciones propuestas de enfoques exactos y heurísticos para la secuenciación de paradas equilibra la necesidad de resultados precisos mientras se evita el sobreajuste del modelo global para casos de recorrido adicionales.
Considerar las limitaciones ayuda a analizar la propuesta, sugerir mejoras y orientar futuros trabajos.
Principales fuentes de error
Los principales errores identificados en el procedimiento global de la propuesta son los siguientes:
Pérdida de secuencias de zonas de interés en el modelo de regresión debido a la agrupación de siete zonas y a la repetición limitada de zonas en rutas dentro de la misma ciudad.
La precisión de una matriz de coste personalizada depende de la calidad de los datos utilizados para crearla. Si los datos son inexactos o incompletos, la matriz de coste no será precisa.
Mayor variabilidad de la información temporal en comparación con las mediciones de distancia relativamente estáticas.
A diferencia de las mediciones de tiempo, diferentes distancias pueden medirse en diferentes unidades (por ejemplo, millas y kilómetros) según la fuente.
Alta variabilidad de los atributos de la ruta, lo que plantea desafíos para determinar combinaciones de enfoques metaheurísticos y heurísticos mientras se mantiene un equilibrio entre rendimiento y diferencias en la puntuación.
Estos errores tienen un impacto significativo en los resultados finales y dificultan alcanzar resoluciones óptimas. Sin embargo, a pesar de estas limitaciones, el proyecto aún cumple con el objetivo de precisión satisfactoria dentro de su alcance.
Posibilidades de investigación futura
La logística y las técnicas de optimización están en constante evolución con la tecnología, con el objetivo de ofrecer mejores servicios. Este proyecto puede expandirse dentro de la misma área de investigación y temas complementarios para ofrecer contribuciones originales para cuestiones complejas en entornos académicos y comerciales.
Las posibilidades futuras incluyen extender los algoritmos propuestos a contextos similares y compartir herramientas con entidades relevantes. Se haría hincapié en la difusión y en aumentar la visibilidad del proyecto, asegurando la compatibilidad funcional con aplicaciones y desarrollando software fácil de usar.
Otra posibilidad es explorar el problema de enrutamiento de carga, utilizando perspectivas cuánticas, como los anulares adiabáticos, métodos variacionales y aprendizaje cuántico. Estos enfoques abordan la complejidad combinatoria y aprovechan el potencial de la computación cuántica para la gestión, análisis y procesamiento de datos masivos. Se alinean con la creciente demanda de optimización en logística de transporte y atraen a científicos e ingenieros de todo el mundo para colaborar en estrategias de optimización de enrutamiento.