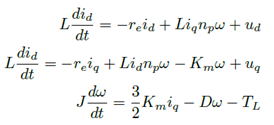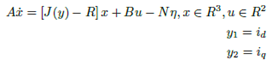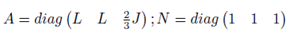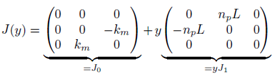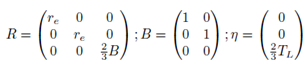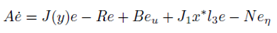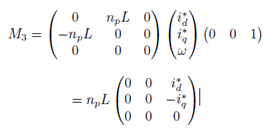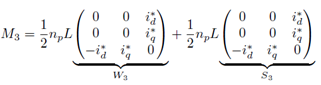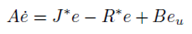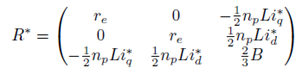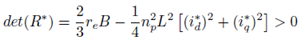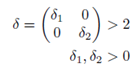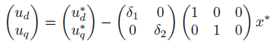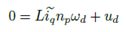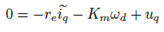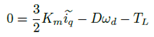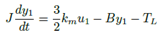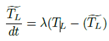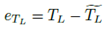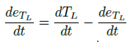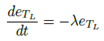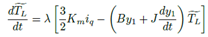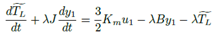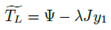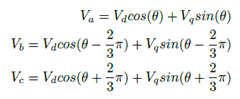Forma sugerida de citación:
Mayoral Lagunes, R.; Juárez Abad, J. A.; Aguilar López, B. A.; Linares Flores, J. y Barahona Ávalos, J. L. (2020). «Control de velocidad de un motor síncrono de imanes permanentes accionado por un inversor trifásico multinivel». Ingenius. N.° 23, (enero-junio). pp. 97-108. doi: https://doi.org/10.17163/ings.n23.2020.09.
1. Introducción
Los motores eléctricos son actuadores que se utilizan en la mayoría de la maquinaria industrial y en electrodomésticos; su posición y/o velocidad son controladas para que puedan cumplir con alguna tarea específica, entre las que podemos encontrar: máquinas CNC, bandas transportadoras, robótica y otros procesos industriales. Dentro de estas aplicaciones es común encontrar motores síncronos de imanes permanentes (MSIP), los cuales tienen una mejor precisión en términos de velocidad y posición debido a su propiedad de sincronía. Recientemente, los controladores que permiten modificar dichas magnitudes se realizan por medio de dispositivos reprogramables y reconfigurables, tales como DSP y FPGA respectivamente [1, 2].
Para este tipo de motores se han propuesto diversos esquemas de control tales como el control basado en pasividad mostrado en [3] y el de un controlador basado en la técnica Backstepping para el seguimiento de posición el cual se muestra en [4].
Los MSIP deben ser accionados por medio de un inversor trifásico, el cual preferentemente deberá entregar una onda de voltaje con la menor cantidad de armónicos posibles, ya que en caso contrario se pueden generar algunos daños bien conocidos, tanto en la parte eléctrica como en la parte mecánica del motor [5]. En este trabajo, se construye un inversor trifásico multinivel de cinco niveles, con el cual se reduce el contenido armónico y mejorar así la calidad del voltaje de alimentación hacia el motor [6]. Una característica adicional de este tipo de convertidor es que maneja mayor potencia, pues esta se distribuye en los arreglos en serie que conforman los dispositivos de conmutación [7 – 9].
Este trabajo está estructurado de la siguiente manera, en la sección 2 se describe brevemente el sistema a controlar, a continuación, en la sección 3 se describe la metodología empleada centrada para la implementación de sistemas de procesamiento en FPGA tomada de [10–14]; dicha metodología posee dos fases las cuales son tratadas en las secciones 4 y 5. Posteriormente en la sección 6 se describe la construcción del convertidor de potencia empleado, en este caso el inversor trifásico multinivel de cinco niveles y finalmente en la sección 7 se presentan los resultados experimentales obtenidos.
2. Descripción del sistema
Se implementa un control basado en pasividad para el seguimiento suave de la velocidad de un motor síncrono de imanes permanentes, accionado por un inversor trifásico de topología en cascada de 5 niveles. Esto se realiza empleando un dispositivo de lógica reconfigurable.
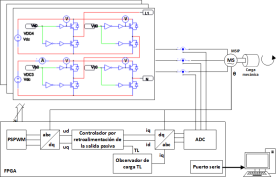
En la Figura 1 se muestra el esquema del sistema propuesto. El MSIP está accionando una carga mecánica desconocida, la alimentación del motor es suministrada por el inversor trifásico de 5 niveles. El controlador basado en pasividad, el procesamiento de señales y el modulador PS-PWM son implementados en un FPGA.
3. Metodología
De acuerdo con la metodología empleada, tomada de [8], este trabajo se divide en 2 fases, la primera de las cuales, de manera general tiene que ver con el modelado del sistema y el análisis de las propiedades matemáticas de este modelo para realizar la formulación del controlador del sistema. La segunda fase trata sobre la implementación del algoritmo de control formulado en la fase 1 y los módulos complementarios los cuales serán implementados en el dispositivo de lógica reconfigurable. Cada una de estas fases se describe con mayor detalle a continuación.
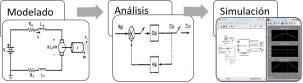
La fase 1 se resume de manera gráfica en la Figura 2. Esta fase es independiente del dispositivo a utilizar en la implementación y se divide a su vez en 3 etapas:
-
1. Modelado: En esta etapa se modelan matemáticamente el MSIP y el inversor trifásico multinivel empleando las leyes o teoremas necesarios para la obtención de las ecuaciones diferenciales del sistema.
2. Análisis: Se analizan los modelos dinámicos de la combinación inversor-motor y por medio de herramientas algebraicas, se diseña el controlador propuesto y se determina la factibilidad de todo el sistema.
3. Simulación: En esta etapa se simulan los modelos matemáticos obtenidos para confirmar la aproximación al sistema real; para ello se utiliza el software Matlab/Simulink en cosimulación con el software PSIM.
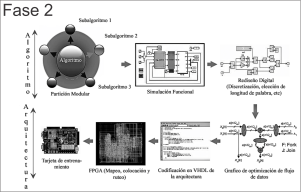
Para la fase 2, la metodología de diseño propuesta se resume en la Figura 3 la cual cuenta con 7 etapas. Esta propuesta es una solución equilibrada entre dos necesidades opuestas: 1) un método amigable que se adapta perfectamente a un ingeniero de control que no es un experto en diseño digital y 2) obtener un buen rendimiento del sistema control [10]. Las etapas mencionadas se describen a continuación:
-
1. Partición modular: Consiste en dividir el algoritmo en bloques reutilizables que tienen sentido desde un punto de vista funcional, es decir, el algoritmo de control y el modulador del inversor se dividen en módulos y se identifican aquellos que puedan ser reutilizables como operaciones, codificadores, tablas de búsqueda, etc. Se trata de dividir el diseño en partes más pequeñas que puedan ser manejables.
2. Simulación funcional: En esta etapa el controlador se valida en función de bloques en tiempo continúo empleando por ejemplo el software MATLAB-Simulink.
3. Rediseño digital: Esta etapa es muy importante, ya que se incluye la realización del filtro digital, la elección del periodo de muestreo, la elección del formato de coeficientes y variables acorde con las necesidades y restricciones del control tales como: longitud de palabra, punto fijo o punto flotante, entre otros. Las cuatro etapas finales son para la implementación basada en FPGA y consisten en lo siguiente:
4. Gráfico de optimización del flujo de datos: En esta etapa se modela el flujo de datos del algoritmo para tener el mejor balance en términos de tiempo/área, para esto se obtiene una representación gráfica de cada módulo del algoritmo. La representación gráfica está compuesta de líneas y nodos, cada línea corresponde a una transferencia de datos y los nodos representan operaciones aritméticas o funciones lógicas o matemáticas.
5. Codificación HDL: A partir del gráfico de flujo de datos de la etapa anterior se transcribe a código VHDL; las transferencias de datos por lo regular son controladas por máquinas de estados finitos síncronas a la señal de reloj del FPGA.
6. Implementación en FPGA: Este es un proceso automático y es realizado por lo regular con la herramienta que proporciona el fabricante del dispositivo, en esta etapa se realiza el mapeo de las funciones resultantes, colocación y ruteo.
7. Validación experimental: Consiste en integrar todo el sistema, se realizan pruebas de rendimiento, y se ajustan los parámetros necesarios hasta obtener los resultados deseados.
4. Fase 1 de la metodología
4.1. Control por ETEDPOF, modelado y análisis
Partiendo del modelo d − q obtenido de las ecuaciones del modelo matemático original obtenido en [15], se calculan los voltajes de entrada u = [uduq] y las corrientes de entrada i = [idiq] en el eje coordenado d − q. Para el diseño del controlador se supone que se conoce la velocidad angular y el par de carga. Para comenzar con el diseño del controlador por retroalimentación de la salida pasiva, se considera el siguiente modelo en el eje coordenado d − q[3]:
Representando el sistema de ecuaciones (1) en su forma matricial y reescribiéndolo en su forma pasiva, se tiene lo siguiente [16]:
Donde:
El vector de estados está compuesto por:
J0 y J1 son matrices constantes y antisimétricas, y es un escalar que representa la salida del sistema y, además, es una de las variables del vector de estado x; R es una matriz simétrica semidefinida positiva, B es una matriz constante de las entradas de control y finalmente n es un vector de pares de carga. Para comprobar que el sistema promedio no lineal del MSIP dado en (1) es pasivo, se hace uso de las definiciones de pasividad y disipatividad tratadas en [3].
Sea u* € R2 la cual denota la trayectoria de entrada nominal correspondiente a la trayectoria del vector de estado nominal x*(t) € R3 . Partiendo de ello se construye la dinámica de referencia del sistema, la cual debe satisfacer la siguiente expresión:
Se define el error de seguimiento e = x – x*, el error de la entrada de control eu = u−u*, y el error de la entrada de la perturbación eh = h − h* y tomando en cuenta que J(y) = J0 + yJ1 , entonces:
Definiendo a M3 = J1x*l3 como una matriz de 3×3, dada por:
Después la matriz M3 se descompone en dos matrices mediante la utilización del álgebra de matrices, y así, se consigue una matriz simétrica y una matriz antisimétrica, teniendo como resultado:
Posteriormente W3 se suma a la matriz conservativa J(y), y S 3 se suma a la parte disipativa R. Con esta operación se consigue la ecuación de la dinámica del error de seguimiento, expresada como:
Si se considera a R* > 0, es decir, definida positiva entonces se satisface la siguiente condición:
Haciendo uso del criterio del Sylvester, se verifica que R* > 0, es decir, que es una matriz semidefinida positiva, por tanto, se debe cumplir que:
Siguiendo con la metodología de diseño del controlador, mediante Lyapunov, se propone a eu como eu = −dBT e, donde:
Siendo
De la Ecuación (12) obtenemos las leyes de control que actuaran sobre el sistema, quedando de la siguiente forma:
4.1.1. Puntos de equilibrio
Los puntos de equilibrio nos servirán para calcular las variables de referencia deseadas i*d, i*q, u*d, u*d, w*. Para este caso w* es el valor de la velocidad deseada que se medirá en la flecha del motor. Para obtener estas referencias se toma el conjunto de las ecuaciones (1) y se igualan las derivadas a 0, por tanto, se obtienen las siguientes expresiones:
Despejando se obtiene:
4.1.2. Diseño del observador del parámetro del par de carga
Para diseñar y desarrollar un controlador eficiente y robusto, es necesario conocer todas las variables que perturban al sistema. Debido a que el controlador por retroalimentación de la salida pasiva del error, no es robusto ante perturbaciones de par de carga constante, se diseña un observador de orden reducido para estimar el parámetro de par de carga junto con los términos de fricción no modelados [17]. Se define la corriente de cuadratura iq como la entrada de control, u1 = iq y se define a la velocidad angular estimada como la salida medida, y1 = w. Los valores nominales de los parámetros, J y Km se consideran conocidos. Sustituyendo las variables u1 y y1 en la ecuación mecánica dada en (1), se obtiene la siguiente expresión:
Se propone el siguiente observador de par de carga como:
Donde
Considerando TL
constante se tiene 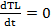 , sustituyendo (19) en (21), se obtiene la siguiente dinámica del error de estimación:
, sustituyendo (19) en (21), se obtiene la siguiente dinámica del error de estimación:
Escogiendo una ganancia
Despejando y reordenando la ecuación anterior, se obtiene la siguiente expresión:
Realizando el cambio de variable
El valor estimado del parámetro de par de carga junto con los términos de fricción desconocidos ~TL, se adaptan en línea a la ley de control de seguimiento suave de velocidad angular. El propósito de esta adaptación es disminuir los efectos producidos por la carga aplicada al eje del MSIP.
4.2. Simulaciones en MATLAB del controlador
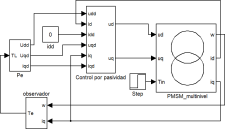
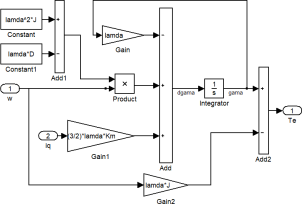
Con el uso del software MATLAB-Simulink se procede a hacer el diseño en diagrama de bloques de todo el sistema. En la Figura 4 se muestra el diagrama a bloques principal.
El controlador por pasividad mostrado en la Figura 4 está basado en el conjunto de ecuaciones (12), la implementación en bloques se muestra en la Figura 5.
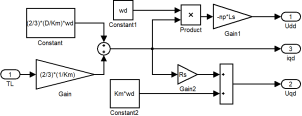
El observador de carga de las ecuaciones (25) y (26) se muestra en bloques en la Figura 6.
Las ecuaciones (17) de los puntos de equilibrio del sistema, que se utilizan para encontrar las referencias y trayectorias deseadas se muestran a bloques en la Figura 7.
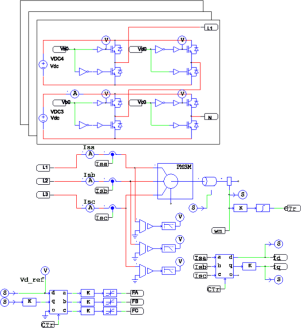
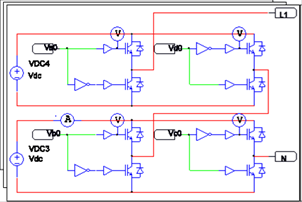
Para validar el funcionamiento del sistema se realiza la cosimulación con Simulink y Psim. El diagrama eléctrico en Psim del inversor multinivel en conjunto con el motor MSIP se muestra en la Figura 8. Se puede observar que el inversor multinivel se compone de tres secciones iguales como la mostrada en el recuadro de la izquierda de la Figura 8.
4.3. Inversor multinivel
Para este trabajo se utiliza un inversor multinivel de celdas en cascada. Esta configuración se basa en celdas conectadas en serie para sumar los voltajes y obtener los 5 niveles deseados como se muestra en la Figura 9.
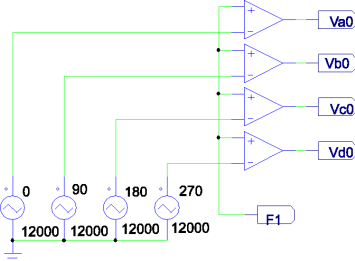
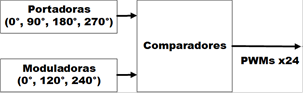
La técnica de modulación empleada es PS-PWM, la cual consiste, para el caso de un inversor de 5 niveles, de cuatro señales triangulares llamadas portadoras, desfasados entre sí 90°, es decir, 0°, 90°, 180° y 270°, respectivamente; para este caso las portadoras se generan a una frecuencia de 12 kHz. Estas señales se comparan con una función sinusoidal llamada moduladora, para el caso en cuestión, dicha moduladora está generada por la transformación dq-abc. De manera general su funcionamiento consiste en obtener unos y ceros lógicos por medio de la comparación de la portadora y moduladora; si la señal portadora es mayor o igual a la moduladora, se obtiene un uno lógico, y en caso contrario se tiene un cero lógico. De esta manera, se generan las señales PWM que activan los dispositivos de conmutación. Cabe aclarar que cada fase contiene una moduladora desfasada 120° con respecto a las otras fases, por lo tanto se tiene un total de 24 señales PWM, 12 canales principales con sus 12 señales complementarias. En la Figura 10 se muestra el diagrama para generar la modulación PS-PWM solo para una fase con sus cuatro señales principales.
4.4. Resultados de simulación
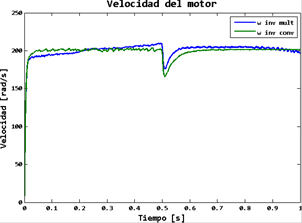
A continuación, se muestran los resultados obtenidos de la cosimulación del sistema ante diferentes escenarios y así mostrar una comparativa. Estos escenarios son: el modelo del MSIP de Psim accionado por un inversor trifásico convencional y finalmente accionado por el inversor trifásico multinivel de cinco niveles. En ambos casos es aplicado el controlador por pasividad diseñado. Como resultado de la simulación, en la gráfica de la Figura 11 se puede apreciar la velocidad angular del motor accionado ambos tipos de inversor. En dicha gráfica puede observarse que cuando se aplica un cambio en el par de carga en la flecha del motor, en el tiempo t = 1s, la perturbación provocada por dicho cambio es efectivamente contrarrestada por el controlador. No existe una diferencia apreciable entre un tipo de inversor y otro.
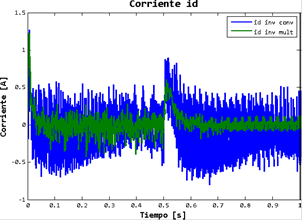
En la Figura 12 y 13 se muestran las gráficas de las corrientes id, iq respectivamente en las condiciones ya mencionadas. Es importante hacer notar que con el uso de un inversor multinivel el rizo en las corrientes disminuye de manera considerable por el uso combinado de dicho inversor y el controlador diseñado.
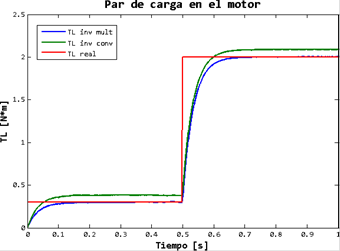
Finalmente, en la Figura 14 se muestra la estimación del par de carga. Se puede apreciar que en el observador diseñado igualmente funciona mejor en el caso del inversor multinivel, lo que comprueba su funcionamiento correcto.
5. Fase 2
En esta fase se realiza la programación del FPGA. Cabe mencionar que en este trabajo la codificación se realiza directamente en el lenguaje VHDL, sin emplear ningún generador de código, este enfoque permite hacer uso óptimo de los recursos del dispositivo.
5.1. Implementación del módulo del modulador PSPWM
El modulador fue programado en el software ISE DESIGN de XILINX en lenguaje VHDL, por simplicidad en la Figura 15 se muestra el diseño por medio de un diagrama esquemático a bloques. Los bloques programados principales son: bloque de portadoras que es donde se generan las señales triangulares; el bloque de moduladora, es el que genera la señal moduladora; finalmente, los comparadores generan las señales PWM para realizar la comparación de las portadoras con la moduladora.
5.2. Implementación del módulo del controlador
El controlador está dividido en varios submódulos: transformación abc-dq, transformación dq-abc, observador de carga, puntos de equilibrio, control de velocidad basado en pasividad, lectura de los sensores de corriente, lectura del sensor de posición/ velocidad. Estos módulos trabajan con el estándar IEEE 754 de 32 bits de precisión simple que es el formato numérico más utilizado en hardware[18].
5.2.1. Módulo transformado dq - abc
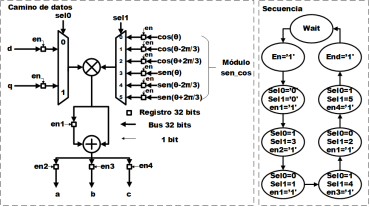
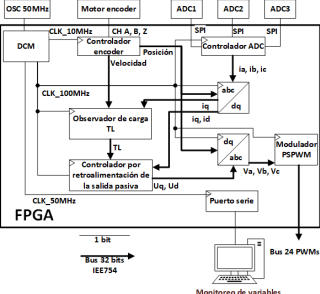
Para el desarrollo de este módulo se realiza la arquitectura mostrada en la Figura 16, la cual es de ayuda para la solución en línea de la Ecuación (27) y la optimización de recursos. En el caso de este módulo se utiliza un multiplicador, un sumador y un registro, todos estos elementos se encuentran dentro del FPGA, sin embargo, al ser limitados se debe de optimizar su uso. Como se observa en la Figura 16, este requiere 8 entradas: d, q y las 6 funciones trigonométricas. A la salida tenemos los valores a, b y c, los cuales representan el valor del voltaje de las fases. Posteriormente en la Figura 17 se muestra la implementación en el hardware de las ecuaciones (27), esta metodología fue tomada de [19]. Dado la complejidad del sistema para ejemplificar el desarrollo, solo se muestra este módulo, sin embargo, la construcción de los demás módulos del sistema se realiza de manera similar. En la Tabla 1 se muestra el consumo de recursos lógicos en el FPGA después de realizar la implementación de todos los módulos implicados en el diseño y en la Figura 18 se presenta el diagrama de más alta jerarquía del sistema.
6. Plataforma experimental
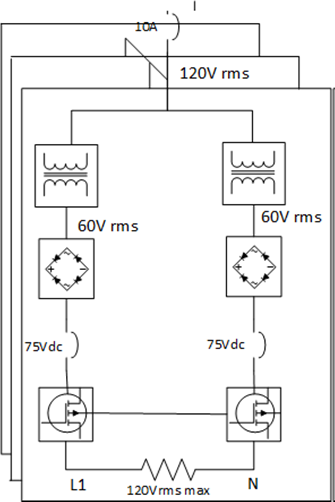
La configuración eléctrica de la plataforma del inversor multinivel se muestra por medio del diagrama unifilar mostrado en la Figura 19.
En la Figura 20 se muestra la plataforma experimental construida y empleada para las pruebas de laboratorio. Las señales de control son generadas por el FPGA, que sirven para conmutar el inversor multinivel y generar la potencia necesaria para impulsar al MSIP de acuerdo con la trayectoria de referencia deseada. La plataforma experimental está conformada por los siguientes elementos:
-
• Fuentes de CD aisladas
• Puentes-H
• Centro de carga principal
• Fuentes de CD aisladas
• Transformador de la fuente de CD
• Puente de diodos
• Capacitores de la fuente de CD
• Riel Din
• Clemas de conexión
• Interruptores de protección
6.1. Kit de desarrollo ALINX
El kit de desarrollo utilizado es de la marca ALINX modelo AX309 mostrado en la Figura 21, este cuenta con un FPGA SPARTAN-6 XC6SLX9, el cual es una plataforma de desarrollo de bajo costo, con las siguientes características:
7. Resultados experimentales
Dado que el procesamiento al interior del dispositivo FPGA es numérico, es necesario contar con un medio para obtener la lectura de las diferentes señales que se procesan, para ello se toman lecturas de las señales y se envían por medio del puerto serial/UART a una velocidad de 921 600 bps, una vez que se reciben en la computadora son procesadas y se presentan por medio de una GUI diseñada en LabView, los parámetros medidos son la velocidad (
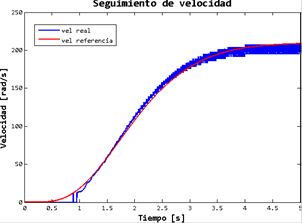
Por otra parte, el MSIP se encuentra acoplado en su flecha a un motor de corriente directa (CD) que funciona como carga mecánica externa como se puede ver en la Figura 22. A continuación, en la Figura 23, se muestra la velocidad angular
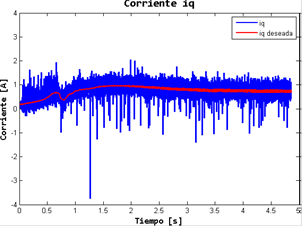
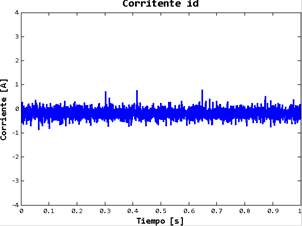
Durante el mismo periodo de tiempo en la Figura 24. Se muestra el seguimiento de la corriente iq al arranque del motor, estableciéndose en 0.5 amperes; esta es la corriente activa que es aprovechada por el motor y es transformada en par mecánico. De igual manera, en la Figura 25 se muestra la regulación de la corriente id , esta debe mantenerse en 0 amperes dado que es la corriente reactiva que no es posible aprovecharla. Ambas corrientes mostradas por igual muestran rizo el cual se debe a la resolución de los sensores de corriente empleados. Finalmente, en la Figura 26 se muestra la estimación del par de carga en el eje del motor durante el mismo periodo de tiempo, la cual al llegar a la velocidad deseada se establece en 0.4 Nm.
8. Conclusiones
Con base en los resultados de simulación y los resultados experimentales se puede argumentar que el controlador por retroalimentación de la salida pasiva diseñado e implementado lleva a cabo de manera adecuada el seguimiento y regulación de la velocidad angular del MSIP. Por otro lado, se verifica que el estimador de orden reducido del par de carga, estima correctamente este parámetro. De manera adicional, en términos de hardware, se observa que el inversor multinivel reduce considerablemente la distorsión armónica de voltaje, lo que se traduce en menor ruido en el sistema en general y evita la necesidad de utilizar filtros. Gracias a las particularidades del dispositivo digital (FPGA) donde se realizó la implementación, se logra un periodo de muestreo de 10
Como trabajo futuro se pretende implementar un algoritmo más complejo, tal como un estimador algebraico, para lograr una mejor estimación del par de carga mecánico. Lo anterior sería posible aprovechando la característica principal del FPGA que es el paralelismo.