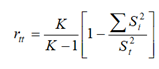Introducción

Las estrategias instruccionales para el aprendizaje o de enseñanza, son medios o recursos que coadyuvan la orientación pedagógica y las necesidades individuales del entorno del estudiante, con la finalidad de desarrollar las actividades prioritarias para el aprender a aprender o aprender a pensar, con el sentido de hacerlo versátil, ameno y acumulador de logros académicos para el mismo.

Estas estrategias, son acciones utilizadas por el docente para promover un proceso interactivo y colaborativo, entre él y los estudiantes, destacando su rol como orientador y promotor del proceso de aprender a aprender del alumno, todo esto enmarcado dentro de las diferencias individuales y las características del contexto, en la construcción de un aprendizaje significativo en proyección hacia el bien común. (^{Romero, 2019})

En tal sentido, busca que el estudiante aplique el conocimiento en las situaciones personales, académicas o laborales y considere las diferencias individuales, las características del entorno, la calidad de los materiales y equipos, así como también el uso y manejo de las tecnologías de información y comunicación que conjuntamente con el tiempo de ejecución de las actividades, contribuyan a la calidad del entorno educativo.

Desde esta perspectiva que se ha trabajado, es conveniente destacar los tipos de estrategias instruccionales para un aprendizaje significativo, las cuales se han dividido en tres aspectos, definidos como preinstruccionales, coinstruccionales y postinstruccionales, asimilado y reconocido por muchos autores, en las cuales están incorporadas los tres momentos de una clase en el proceso de aprendizaje.

Al respecto, las estrategias preinstruccionales se presentan antes del contenido o material a trabajar y son utilizadas para activar expectativas positivas en los estudiantes, para promover la evocación de conocimientos o experiencias previas pertinentes al tema a tratar, en búsqueda de la contextualización. Algunas de las más representativas son los objetivos y los organizadores previos.

Resulta oportuno destacar, que en el contexto del Cálculo I (diferencial), como estrategias preinstruccionales es relevante avivar los conocimientos previos matemáticos, tales como las operaciones básicas matemáticas de números reales, funciones, límites y la derivada, necesarios para la resolución algebraica y gráficamente, de los problemas de casos reales, contextualizada al área de la ingeniería con significancia para los alumnos del curso.

Al respecto, expresa ^{Colina (2017}), que a los estudiantes de Cálculo Diferencial no captan los significados institucionales y peor aún, los significados personales no son adecuados, y afirma que los conocimientos previos, pueden representar un elemento fundamental a las observaciones expresadas por los estudiantes se desprende interpretativamente, que en los procesos de asimilación, acomodación no han sido las adecuados para captar los significados institucionales del tema en este caso de límite, luego de su investigación en referencia a la definición inmersa en el cálculo diferencial.

Por otro lado cabe referirse, a las estrategias coinstruccionales, las cuales se utilizan durante el proceso en sí educativo, de manera que a través, de la interacción entre los actores en el proceso, estos organizan y estructuran, la información necesaria para la comprensión del nuevo conocimiento o material, e incorporarlo de manera significativa y contextualizado en sus estructuras cognitivas.

De manera semejante, las estrategias postinstruccionales están presentes como cierre, son utilizadas tanto para el aprendizaje (empleadas por el profesor) como de aprendizaje (cuando son trabajadas por el estudiante), con el sentido de profundización y reforzamiento del proceso cognitivo al cierre de la actividad, también pueden ser empleadas por el estudiante, como una autoevaluación formativa en su proceso de aprendizaje

Es pertinente destacar, que en el aprendizaje de la definición de la derivada de funciones de una variable, inmersa dentro del estudio del Cálculo diferencial, se presentan varias dificultades dado que la enseñanza tradicional, en relación a los procesos de derivación, muchas veces se limita solo a la utilización de fórmulas para derivar, y no se muestra al estudiante la importancia en la aplicación de los problemas de ingeniería, como la razón de cambio de una cantidad respecto a otra, y este desapego en la a utilidad es lo que genera un alto grado de desmotivación en ellos y como consecuencia un alto índice de aplazados en estos tópicos.

Por consiguiente, y luego de hacer referencia a los planteamientos que anteceden, es pertinente mostrar, las cifras de desertores en la Universidad del Cesar, oscila entre el 59% y el 76%, durante dos semestres por año durante 4 años consecutivos, desde 2014 hasta 2017, (Departamento de Matemáticas y Estadísticas, 2018). Al respecto, agrega ^{Romero (2019}), que el índice de aplazados y desertores en universidades Venezolanas, es de un 70 % aproximadamente, en los períodos comprendidos entre los años 2014 y 2017, lo cual puede deberse a múltiples factores, tales como, un currículo anacrónico desactualizado, la poca motivación al logro en algunos docentes, insuficiente presupuesto para el sector universitario, entre otros factores, los cuales infieren en el rendimiento académico.

En tal sentido, el propósito de esta investigación es analizar las estrategias instruccionales para el aprendizaje significativo de la definición de la derivada de funciones de una variable, definición emblemática para la excelente prosecución de los estudios académicos en el área de la ingeniería, así como los trabajos de aplicaciones en sus aéreas de trabajo.

Metodología

El contexto del estudio estuvo enmarcado dentro del paradigma epistemológico positivista, de tipo descriptiva, dado que proporciona mayores explicaciones de los eventos, los cuales constituyendo la base y el punto de partida para el desarrollo de la investigación. Su diseño fue de campo no experimental transeccional, puesto que la información se tomó del contexto natural sin ser perturbada en un solo momento, al inicio de la misma, para diagnosticar y determinar la situación de los actores (estudiantes y profesores) y el contexto en el cual estaban inmersos. El tratamiento fue a través de la estadística descriptiva, considerada la investigación cuantitativa, para su análisis, conclusiones y recomendaciones.

Para esta investigación, se tomó como muestra a todos los seis (6) docentes de la asignatura Cálculo Diferencial de la FIUPC; constituyendo la totalidad de la población profesoral y un número de estudiantes de cuatrocientos noventa y cinco (495), que por ser este un número alto, se aplicó el cálculo del tamaño muestral y se seleccionó un número representativos de unidades de la población.

Por tanto, para poder estratificar la muestra, se utilizó la ecuación estadística, que se expresa a continuación,

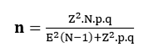(Elaboración ^{Sierra, 2001})

Dónde:

n: tamaño de la muestra.

N: tamaño de la población = 495

p: probabilidad de éxito esperado = 95%

q: probabilidad de fracaso 1- p = 1- 0,95 = 0,05 =5%

E: error seleccionado por el investigador = 5%

Z: nivel de confianza de 95% = 1.96

Luego de realizar el proceso de selección de la muestra, el objeto de estudio quedó conformado por seis (6) docentes, siendo muestra censal muestral, y sesenta y cuatro (64) estudiantes, para un total de setenta (70) sujetos que fueron encuestados en FIUPC de la asignatura Cálculo Diferencial.

Se utilizaron como instrumentos de recolección de datos, dos cuestionarios, el primero para los docentes y el segundo adaptado para los estudiantes, de treinta y tres (33) ítemes estructurados con la opción de ser contestadas con cinco (5) alternativas de respuesta: Siempre (5), Casi Siempre (4), A veces (3), Casi Nunca (2), y Nunca (1), siendo este modo de respuesta denominado escala Likert.

Para determinar la validez de contenido de los instrumentos, se solicitó el juicio de cinco (5), expertos uno en el área de metodología y cuatro (4) docentes especialista del área del Cálculo; quienes aportaron sugerencias sobre la relación y pertinencia de los mismos.

En cuanto a la confiabilidad de los instrumentos se aplicó una prueba piloto a dos (2) docente y diez (10) estudiantes del curso de Cálculo Diferencial, para un total de doce (12) sujetos; no pertenecientes a la muestra de la investigación con el fin de evitar la contaminación; con características similares a la que forma parte de la población en estudios; para evaluar dicha confiabilidad de los instrumentos se empleó el coeficiente Alfa de Cronbach es una de las técnicas que permite establecer el nivel de confiabilidad que es, junto con la validez, un requisito mínimo de un buen instrumento de medición presentado con una escala de tipo Likert.

El cálculo y resultado de dicha fiabilidad se obtuvo con gran eficacia del Programa de Microsoft Excel, por el procedimiento del coeficiente Alfa de Cronbach, el cual queda expresado mediante la siguiente ecuación,

Ecuac. 2

Dónde:

r_tt = coeficiente de confiabilidad

K = número de ítems

Si = varianza de los puntajes de cada ítems

St = varianza de los totales.

De igual manera, para poder conocer los valores que se seleccionaron para mediar la confiabilidad del instrumento, se construyó un baremo de escala del coeficiente de confiabilidad de alfa Cronbach ^{Hernández y Mendoza (2018}), para su interpretación, el nivel de frecuencia medido y el intervalo obtenido según el baremo de interpretación, se obtuvo para la variable un 0,95 para los estudiantes y 0,93 para los docentes, indicando una muy alta confiabilidad y pertinencia de los instrumentos de los docentes y estudiantes de la FIUPC de la asignatura Cálculo Diferencial.

Las técnicas de análisis utilizadas, se aplicaron de acuerdo con el enfoque epistemológico de la investigación, siendo necesario el empleo de estadística descriptiva, para analizar las estrategias instruccionales empleadas para el aprendizaje significativo de la definición de derivada de funciones de una variable. Estas técnicas se aplicaron utilizando el programa SPSS versión 20.

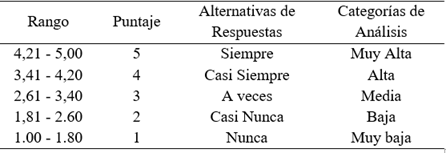
Asimismo, se construyó un baremo de estudio con el fin de analizar los resultados, de los cuestionarios, obtenidos de la aplicación tanto a los estudiantes como a los profesores, los cuales se presentan en la Tabla 1, donde se visualizan la codificación realizada con el fin de establecer los puntajes o calificaciones para las alternativas de respuesta.

Tabla Nº1. Baremo de Análisis 

Fuente: Elaboración propia

Finalmente se hizo el análisis de los resultados, confrontando los valores obtenidos en sus puntuaciones altas o bajas entre el grupo de estudiantes y docentes objetos de estudio, con los planteamientos de varios autores, para así proceder a expresar en una síntesis las conclusiones por objetivo y recomendaciones pertinentes

Resultados

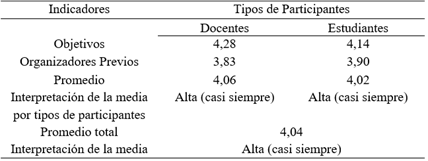
En la Tabla 2, se visualiza el comportamiento de mayor porcentaje de las estrategias preinstruccionales, en la aplicación de los objetivos, se observa que el personal docente de Cálculo Diferencial de FIUPC, con mayor utilización entre siempre y casi siempre, lo cual dio una media de 4,28 por parte de los docentes, evidenciándose un rango muy alto, similitud con los estudiantes de 4,14 estableciendo un nivel alto para el indicador, lo cual revela una gran descripción con claridad las actividades de aprendizaje con anticipación.

Tabla N2. Estrategias Preinstruccionales 

Fuente: Elaboración propias

Estos resultados destacan la teoría que expone ^{González (2017}), referentes a las estrategias preinstruccionales, donde estas establecen las condiciones, tipos de actividades y forma de evaluación del aprendizaje, como estrategias de enseñanza compartidas con los alumnos, las cuales son las encargadas de generar las expectativas apropiadas, es decir, dar a conocer la finalidad, alcance del material y cómo manejarlo. El estudiante sabe qué se espera de él al terminar de revisar el material, ayuda a contextualizar sus aprendizajes y a darles sentido.

Asimismo, destaca ^{Vera (2017}), que el manejo de las estrategias preinstruccionales, referentes a los objetivos, permiten prever el alcance y sirven como guía del desarrollo de un contenido, y los organizadores previos, tanto para los estudiantes como para los docentes, son relevantes para el anclaje del nuevo contenido a trabajar, las cuales hacen las clase más efectivas en cuanto a la significancia de los mismos.

Con referencia a los organizadores previos, el personal docente de Cálculo Diferencial de la FIUPC, destacó un rango alto de media de 3,83 donde, casi siempre se aplica recurso instruccional introductorio para conocer la información nueva a enseñar; mientras que el estudiantado expresó en mayor porcentaje, apoyándose en la media de 3,90 que, casi siempre se promueve un contexto ideacional activo para asimilar la nueva información, reflejando como los organizadores previos de enseñanza antes de ser presentada la información nueva a aprender.

Dichos resultados, se asimilan al papel fundamental que tiene tanto para la comunidad como para la FIUPC, el ser partícipe de los procesos educativos, haciendo referencia a lo expresado por ^{Romero (2015}), los organizadores previos desarrollan información de tipo introductorio y contextual, los cuales tienden a ser puentes cognitivos entre la información nueva y la previa; por tanto, esta estrategia hace mayor accesible y familiar el contenido; con ello, se elabora una visión global y contextual de la temática a abordar.

A este respecto, destaca ^{Cárdenas (2018}), que el concepto de derivadas considerado desde la visión operacional, se plantearon algunas deficiencias, desde las perspectivas epistemológicas detectados a través de sus concepciones que estos son deficiencia en referencia a los conocimientos previos, de tipo verbal y por utilitarismo; para poder obtener significancia del concepto.

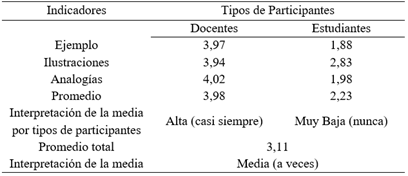
Prosiguiendo con el análisis, se presenta la tabla 3, se visualiza el comportamiento de las estrategias coinstruccionales, sobre la ejemplificación sobre todo desde la perspectiva del contexto, donde los resultados de la encuesta se apoyan en una media de 3,97 por parte de los docentes de Cálculo Diferencial, evidenciándose un rango alto, no ocurre lo mismo en los estudiantes, quienes muestran una media de 1,88 estableciendo un nivel bajo, mostrando de esta manera que se deben promover actividades de ejemplificación sobre todo en el contexto de la aplicabilidad en cada área de la ingeniería, guiadas para impulsar el acto de aprendizaje.

Tabla Nº3. Estrategias Coinstruccionales 

Fuente: Elaboración propia

Desde la perspectiva de las evidencias, estos no tienen similitud con la teoría expresada por ^{Romero (2019}), quien señala que es fundamental definir, qué aprendizajes se espera lograr por los estudiantes, al definirlos no sólo se tendrán en cuenta los contenidos a desarrollar sino la contextualización de los mismos, es decir, hacerlos significativos para ellos; aunque los contenidos sean los mismos, los saberes que se pretenden que se desarrollen, pueden ser muy diferentes dependiendo la visión en su área de trabajo.

Con referencia, a las ilustraciones, el personal docente de Cálculo Diferencial de la FIUPC destacaron que casi siempre, se amplía la gama de información gráfica en los diversos contextos de enseñanza, reflejando un rango alto de media de 3,94 mientras el estudiantado expresó con que casi nunca se utilizan ilustraciones, de media de 1,88 refiriéndose a un muy bajo nivel según el baremo, refiere que no hay una relación espacial esencialmente productiva.

Asimismo es pertinente destacar, la incorporación de las nuevas tecnologías de la información y la comunicación, en auxilio a las ilustraciones y simulaciones necesarias en el área de la ingeniería, a este respecto destacan ^{Robles, y Zambrano (2020}), como las prácticas didácticas ejecutadas a través del uso de las Tics generan ambientes creativos de aprendizajes, generan motivación para aprender, sin limitaciones de espacio y tiempo, desde la perspectiva individual como en equipo, lo cual les permite experimentar dentro y fuera del aula de clases.

En connotación de la estrategia de la analogía, se pudo visualizar que los docentes de Cálculo Diferencial encuestados manifestaron que siempre se aplica la analogía como estrategia para lograr un aprendizaje con comprensión del tópico a estudiar, reflejando una media alta del 4,02; mientras que los estudiantes manifiestan que nunca se les orientan a nuevas experiencias con un conjunto de conocimientos, con una media baja de 1,98 de acuerdo al baremo establecido, denunciando la necesidad de introducir experiencias análogas que ayudan a comprender e internalizar los conceptos al estudiante.

El conjunto de evidencias, tiene un acercamiento a lo expuesto por ^{Barriga (2015}), entendido en este caso, quien asevera que la analogía son proposiciones que indican que una cosa o evento concreto y familiar es semejante a otro, desconocido, abstracto o complejo; estas sirven para comprender información abstracta, trasladando lo aprendido a otros ámbitos.

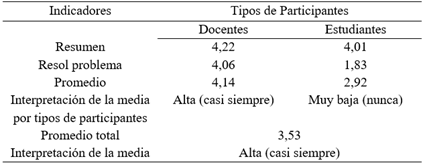
Posteriormente, se presentan los resultados, de la tabla 4, que hace referencia a las estrategias postinstruccionales, según los datos obtenidos el personal docente de Cálculo Diferencial expresó como la estrategia de resumen, donde casi siempre se apoyan en una media 4,22 evidenciándose un rango muy alto, se promueve una organización global adecuada de la información nueva a aprender, pero algo más bajo con un con 4,01 un nivel alto de los estudiantes, manifestaron que casi siempre se facilita la comprensión de la información principal mejorando la decodificación selectiva.

Tabla Nº4. Estrategias Postinstruccionales 

Fuente: Elaboración propia

Asimismo, los resultados obtenidos concuerdan con la teoría de ^{Romero (2015}), cuando plantea que tales estrategias como el resumen permite al estudiante formar una síntesis y abstracción de la información relevante de un discurso oral o escrito. Enfatizan conceptos claves, principios y argumento central; facilitan que recuerde y comprenda la información relevante del contenido por aprender.

Con referencia al indicador resolución de problemas, el personal docente de Cálculo Diferencial de la FIUPC destacaron que casi siempre se asume un papel más activo en la toma de decisiones de la resolución de problemas, reflejando un rango alto de media 4,06 mientras los estudiantes expresaron, que casi nunca se fomenta el análisis de casos para motivar nuevos conocimientos, con una media 1,83 de nivel bajo según el baremo; indicando de esta manera que aunque saben resumir los pasos, la resolución de problemas se les dificulta por la poca comprensión de la derivada como razón de cambio.

En ese mismo sentido ^{Cárdenas (2018}), luego de su investigación, infiere que los estudiantes presentan dificultades para resolver o modelar situaciones problemas que requería mayor dominio de conceptos o propiedades de la derivada de funciones, pero demuestran algunas destrezas cuando se trata de fórmulas o algoritmos matemáticos. Asimismo, destaca este autor que los alumnos asocian la importancia del estudio de la derivada según su aplicabilidad en su área de la carrera y no desde el concepto matemático.

A lo cual agrega, ^{Marín (2018}), el aprendizaje cooperativo para el estudio del cálculo Diferencial mediante la resolución de problemas es considerada de gran impacto en los procesos de enseñanza y aprendizaje, dado que se establecen interacciones individuales que potencian las destrezas interpersonales y grupales emergentes, lo cual logra integrar elementos conceptuales, teóricos y argumentativos; los cuales consolidan como una alternativa eficaz en los procesos de enseñanza y aprendizaje, comparativamente frente a los tradicionales: el individualista y competitivo.

Seguidamente, se presentan los resultados, de la tabla 5, que hace referencia a las estrategias de aprendizaje obtenidas de la aplicación del instrumento elaborado para tal fin, luego de haber desarrollado los resultados, se permite presentar los resultados y análisis desde la perspectiva de la visión de su aplicación.

Tabla Nº5. Estrategias de Aprendizaje 

Fuente: Elaboración propia

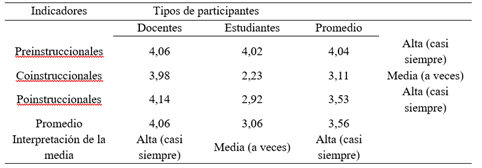
En relación a dichos resultados, para las estrategias preinstruccionales, se puede decir, que casi siempre, identifican dichos métodos que servirán de apoyo dentro del aula de clases, siempre consideran que activan los conocimientos previos de estos o incluso a generarlos en caso de que no existieran, donde cada uno tiende a involucrarse en el proceso de establecer ciertas expectativas en los estudiantes; ratificado a través de la media general de 4,04 categorizada según baremo como alta.

En torno a los resultados, para las estrategias coinstruccionales, se puede decir, que medianamente se utilizan en cada encuentro o sesión de clases, facilitan una jornada de trabajo manteniendo la motivación y expectativas, estas estrategias son aplicadas durante el desarrollo de la acción pedagógica, procurando alcanzar significativamente el aprendizaje en los estudiantes; en este caso con una media de 3,11 según baremo.

Partiendo de los resultados, para las estrategias postinstruccionales, se puede decir, que los docentes de Cálculo Diferencial casi siempre las emplean en la jornada, antes que ésta esté llegando a su fin, lo que le hará conocer al docente el avance de sus aprendices y la calidad de comprensión lograda por cada uno de ellos, ayudando así a los estudiantes a fijar el aprendizaje y fortalecerlo; mientras que los estudiantes la obtienen de sus conocimientos, comprender las temáticas internalizadas, y visualizar con resolución de problemas y analogías aquellas que aún están pendientes para ser consolidadas, dejando mayor claridad para un posterior trabajo; pero estos resultados no están revalidados a través de la media general con 3,53 está categorizada como alta según baremo.

En cuanto a los resultados de forma general de las perspectiva de las estrategias, en la tabla 5, sobre las estrategias de aprendizaje, se puede decir, que con una media del 4,06 alta, del personal docente, casi siempre, estas estrategias son aplicadas y con una media de 3,06 por parte de los estudiantes, medianamente aplicadas por ellos, para internalizar los conceptos dados para el aprendizaje y que este sea significativo; y de manera general de dichas estrategias con una media de 3,56 categorizada como alta, casi siempre aplicadas.

Conclusiones

Una vez finalizada la investigación y luego de analizar las estrategias instruccionales utilizadas para el aprendizaje significativo de la definición de derivada de funciones de una variable, se llegó a las siguientes conclusiones.

En lo que respecta, a identificar las estrategias de enseñanza aprendizaje utilizadas por el profesor para el aprendizaje significativo de la derivada de funciones de una variable, en estudiantes de ingeniería de la Universidad Popular del Cesar, se concluye que las estrategias más empleadas son las preinstruccionales y menos trabajada las coinstruccionales, tanto por los docentes como por los estudiantes.

Asimismo, las más empleadas por los docentes y los estudiantes, son los objetivos, como estrategia de para realizar la planificación del alcance y abordaje del nuevo contenido para el mejoramiento del logro del aprendizaje en los estudiantes, el cual sirve de guía a estos, y de manera de clarificar la meta a alcanzar para el logro del aprendizaje.

No obstante, la menos empleada por los docentes son los organizadores previos, necesarios para vincular los nuevos conocimientos con los preexistentes y los menos trabajados por los estudiantes son la resolución de problemas, parte esencial para la extrapolación de escenarios reales al campo de la matemática y vinculantes con situaciones de su área de trabajo en el futuro.

Por lo tanto, se deben implementar mejores formas para aprender, en aprovechar las bondades de novedosas propuestas, tales como mayor capacidad de visualización de las funciones matemáticas, flexibilidad para aprender de manera individualizada atendiendo al ritmo propio de cada estudiante, acercamiento a la interacción grupal e intercambio de saberes de manera presencial y optimizarlas de manera virtual, empleo de herramientas web para la resolución de problemas matemáticos con implicaciones en la vida cotidiana, por ejemplo.

Se recomienda socializar de manera presencial las discusiones ilustrativas sobre el estudio de la derivada de funciones de una variable. Asimismo, establecer la modalidad de trabajo a distancia para reforzar el aprendizaje colaborativo entre los estudiantes y alternarlo con la modalidad presencial para aclarar dudas en sesiones tipo plenarias, en las secciones de Cálculo de la Facultad de Ingeniería de la Universidad Popular del Cesar.

Se deben reconocer las habilidades cognitivas para potenciar sus destrezas ante una tarea escolar, esto alude a procesos exclusivos y particulares del estudiante que como persona, posee una experiencia distinta ante la vida. Se mantiene el contacto frecuente en la construcción del conocimiento, se controla el proceso de aprendizaje para estimular la comunicación interpersonal, se adapta el nivel de los conocimientos obtenidos de la información.

Es pertinentes destacar, que el nivel de participación e interés por parte de colegas y estudiantes dejó entrever, la afectividad hacia una modalidad mixta para el aprendizaje significativo de la derivada de funciones de una variable, de tal manera que los estudiantes participen mostraron gran interés por resolver problemas que involucran la utilización del concepto de la derivada, muchas veces con éxito, o por lo menos se les vislumbraba la posibilidad de su resolución, tanto desde su trabajo activo como de la ayuda desde el ámbito virtual, en referencia al manejo de simulaciones.

Recomendaciones

Se recomienda socializar personalmente las discusiones ilustrativas sobre el estudio de la derivada de funciones de una variable.

De igual modo es también recomendable, establecer una modalidad mixta de trabajo presencial y a distancia para reforzar el aprendizaje colaborativo entre los estudiantes y alternarlo con la modalidad presencial para aclarar dudas en sesiones tipo plenarias, en las secciones de Cálculo de la Facultad de Ingeniería de la Universidad Popular del Cesar.

Aplicar modalidades mixtas en las secciones de los primeros semestre hasta los últimos semestres de la Facultad de Ingeniería a modo de ir sumando experiencias y voluntades para diversificar el modo de aprendizaje y procurar a través de la modalidad mixta, un aprendizaje significativo de la Derivada de funciones de una variable, en la asignatura de Cálculo.

Así mismo se les recomienda tanto a docentes como a los estudiantes ser más incisivos en el uso de todos los recursos tecnológicos con que cuenta la universidad, así como también la bibliografía amplia y renovada sobre los tópicos de cálculo con que cuenta y ofrece el Departamento de Matemáticas y Estadística, y por ende la Facultad de Ingeniería de la Universidad Popular del Cesar.