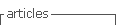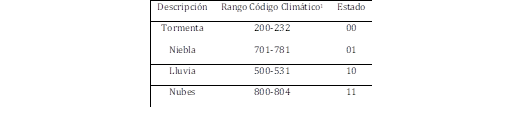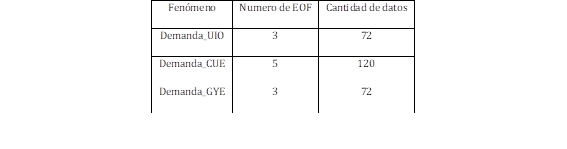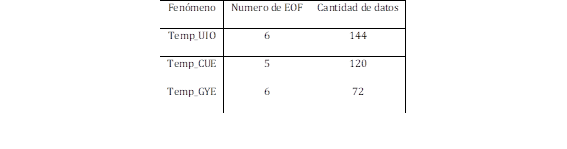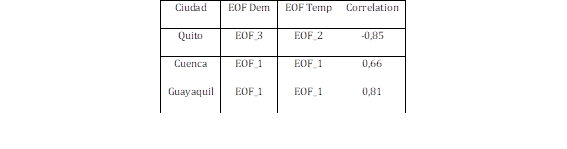INTRODUCCIÓN

El Operador Nacional de Electricidad - CENACE es una entidad estratégica del sector eléctrico ecuatoriano, que opera y administra el funcionamiento técnico y comercial del Sistema Nacional Interconectado - SNI y de las interconexiones internacionales, con criterios de seguridad, calidad y al mínimo costo posible.

En este sentido CENACE en su portafolio de herramientas cuenta con el sistema de gestión de energía EMS mismo que es utilizado para la operación en tiempo real del Sistema Eléctrico de Potencia (SEP) de Ecuador. El SCADA/EMS es un sistema complejo de hardware y software que está conformado por el sistema de adquisición de datos y el sistema central. El sistema de adquisición de datos está formado por unidades terminales remotas (UTR o Gateways) y canales de comunicación que transmiten la información al centro de control nacional (sistema central) formado por servidores de comunicación, servidores de aplicaciones, servidores de base de datos, servidores para almacenamiento de datos históricos, entre otros [1].

Históricamente la adquisición de datos en tiempo real de mediciones de temperatura ambiente de varias subestaciones del SEP se realizaba por medio de sensores de temperatura ubicados en los patios de la subestación, que a través de un transductor a 4-20mA [2] eran leídos por las RTUs ABB400 y transmitían dicha información al SCADA/EMS del Centro de Control.

Dado que estos sensores de temperatura fueron cumpliendo su tiempo de vida útil y ya no cumplían con su función para el envío de información en tiempo real, se implementó un mecanismo alternativo que permite recuperar esta información, generando un valor agregado sobre las condiciones climáticas en diferentes sectores del país donde se encuentran instalaciones que forman parte del SNI. Esta información será de utilidad para la operación en tiempo real y permitirá mejorar la consciencia situacional [3] para la toma de decisiones.

La fuente de información del mecanismo implementado está basado en el uso de una API propia de la página web https://OpenWeathermap.org/api, la cual permite hacer consultas de las condiciones climáticas por ciudad en el mundo. Mediante un componente de software realizado en Python (usando librería Request [4]) se obtiene la información de la API OpenWeather mediante el uso de Web Services [5]. Posteriormente los datos son sometidos a pre-procesamiento, para entregar los datos al sistema SCADA/EMS (información de temperatura y condición climática de determinada de un conjunto de ciudades). Para la presente implementación se realiza la consulta a la API cada 10 minutos, y posteriormente se transmite los datos recibidos hacia el sistema SCADA/EMS de CENACE.

Mediante la arquitectura descrita, la información de condiciones climáticas y de temperatura se procesa en el sistema EMS de forma que sus datos sean visibles en una interfaz gráfica e intuitiva al operador de la Sala de control de CENACE. Esto permite incrementar la conciencia situacional en lo referente a las condiciones climáticas del país.

La información de temperatura obtenida a través de la API es almacenada en la base de datos histórica del sistema EMS, y para motivo de este trabajo ha sido utilizada para el análisis de correlación entre las variables de temperatura y la demanda eléctrica. Varios trabajos han demostrado la existencia de una correlación entre la demanda y temperatura [6]-[14]. En el trabajo de Valor et al. [15] atribuyeron la variación estacional de la demanda de electricidad a las variables meteorológicas y a la tendencia creciente a los factores socioeconómicos. En este trabajo se realizó el análisis del comportamiento de diferentes ciudades en el Ecuador, dándole mayor énfasis a las ciudades de Guayaquil, Quito y Cuenca.

El presente documento está organizado de la siguiente manera: la descripción de la arquitectura del sistema implementado, la adquisición y procesamiento de datos, y la interfaz de visualización gráfica se describen en las secciones 2 y 3. La relación entre temperatura y demanda se presenta en la sección 4, el análisis de los datos y los resultados se muestran en la sección 5, mientras que la sección 6 proporciona conclusiones y recomendaciones.

DESCRIPCIÓN DEL SISTEMA DE ADQUSICIÓN DE DATOS

Como se indicó en la sección 1 de este artículo, la implementación de la arquitectura para la adquisición de datos de temperatura y condiciones climatológicas tiene varios componentes de Hardware y Software. En la Fig. 1 se muestra un esquema general para que el lector pueda familiarizarse con estos componentes.

Figura 1: Arquitectura del sistema de condiciones climáticas 

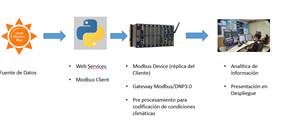
En la Fig. 2 se tiene un diagrama de flujo donde se detalla cómo se transforma la información desde la fuente de adquisición de datos hasta ser almacenada y presentada en el EMS.

Figura 2: Diagrama de flujo del sistema de condiciones climáticas 

La recolección de datos se la realiza a través de la API OpenWeather [16]. Posteriormente se realiza el preprocesamiento de los datos y su transformación mediante un componente de software desarrollado en Python. Este componente es ejecutado de manera periódica para enviar la información procesada a una UTR que tiene una conexión ya establecida con el SCADA/EMS.

El componente desarrollado en Python ejecuta la captura de datos el uso de los servicios web de la API, la misma que despliega la información en formato JSON o XML. De esta estructura de datos se puede recolectar la información de temperatura en grados Kelvin (ºK) y el código de condición climática de la ciudad de interés como se muestra en la Fig. 3.

Figura 3: Salida resultante de la captura de datos a través de Web Service 

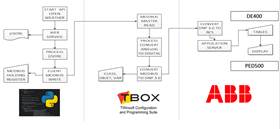
Una vez que identificada la información de interés, se habilita la transmisión de información desde el servidor donde se encuentra alojada el componente ya descrito y a través de protocolo MODBUS [7] transmite la información a una UTR TBOX ubicada en el centro de control nacional. La UTR TBOX de CENACE recibe los valores de temperatura y código climático para luego retransmitirla de manera segura al SCADA/EMS en protocolo DNP 3.0 TCP/IP. La información recolectada mediante el mecanismo descrito anteriormente es finalmente almacenada en los históricos del SCADA/EMS como se aprecia en la Fig. 4.

Figura 4: Presentación tabular de la información de temperatura y condiciones climáticas  

Con la información histórica, se realizó un análisis estadístico descriptivo para determinar los valores típicos de condiciones climáticas para 15 ciudades del Ecuador a través del cálculo de rango máximo, rango mínimo y moda de los datos; para su posterior codificación y transmisión al SCADA/EMS [17] como una señal digital doble, en la cual el valor numérico de condición climática es agrupado en 4 estados: lluvia, niebla, tormenta, y nublado. En la Fig. 5 se muestra la configuración en el EMS para una indicación de cuatro estados.

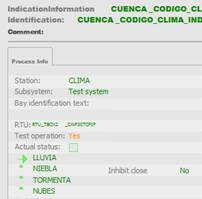
Figura 5: Configuración de señal digital de cuatro estados para representación de condición climática  

La trasformación realizada en la UTR para conseguir representar la condición climática a través de un valor digital de cuatro estados o dos bits, se observa en la Tabla 1, los códigos de clima se obtuvieron del registro JSON como resultado de la solicitud a la API de OpenWeather [16].

El muestreo de información se realiza de la siguiente manera: la petición de información a la API de OpenWeather se realiza cada 10 minutos considerándose que el cambio de temperatura es un proceso lento y este sería el tiempo aproximado con el que se capturaría esta información en campo, el dispositivo Modbus configurado en la UTR realiza una petición de información cada 4 segundos, mientras que la petición de información en el SCADA/EMS a través de protocolo DNP 3.0 TPC/IP es de 6 segundos.

Tabla 1: Relación valor numérico condición climática  

VISUALIZACIÓN GRÁFICA DE DATOS DE TEMPERATURA Y CONDICIONES DE CLIMA EN SCADA/EMS

Una vez que se disponen de datos de las mediciones de temperaturas y códigos de clima en el SCADA/EMS del centro de control nacional, y para que estos datos se conviertan en información valiosa para el operador, se elaboró un despliegue utilizando la herramienta PED500 (herramienta propietaria del SCADA/EMS de ABB versión NM9.2), que es una herramienta que permite el desarrollo de despliegues para su visualización e interacción desde la interfaz humano máquina en las consolas de trabajo de los operadores del centro de control nacional.

Figura 6: Despliegue resultante de isotermas 

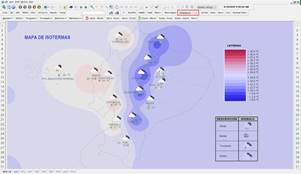
Este despliegue posee la funcionalidad de contorneo de color dinámico, esta funcionalidad se usó para representar la desviación de la temperatura de su valor nominal por medio de áreas concéntricas coloreadas, con esta funcionalidad se consiguió emular un mapa de isotermas como se observa en la Fig. 6; se escogió 25ºC como valor nominal de las mediciones de temperatura. Adicionalmente, se incluyó en el despliegue las señales digitales de condiciones climáticas mediante símbolos gráficos para representar las condiciones de lluvia, niebla, tormenta y nublado.

RELACIÓN TEMPERATURA VS. DEMANDA ELÉCTRICA

En la literatura se puede encontrar evidencias de la relación entre temperatura y el consumo eléctrico [10]-[12]. Dependiendo del fenómeno físico en las que ambas estén involucradas, esta relación puede ser bastante obvia e incluso se pueden diseñar mecanismos para optimizar el consumo eléctrico ante los cambios de temperaturas [13], [14]. En sistemas eléctricos de potencia más grandes, en los que las cargas eléctricas son variadas ya sean de tipo industrial, comercial y/o residencial; la relación entre estas variables ya no es tan evidente. Algunos autores han reportado esta relación como no lineal e incluso se reporta que esta relación es dependiente de la región, el clima y variables socio-económicas [10]-[12].

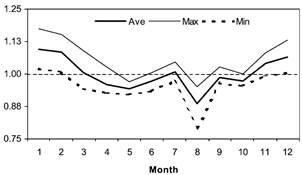
En los trabajos de Bessec et al. [10], Pardo et al. [11] y Sailor et al. [12] muestran la relación de temperatura y el consumo eléctrico mediante un gráfico de dispersión cuyos ejes son: la temperatura y el consumo eléctrico. Este mecanismo visual permite identificar la sensibilidad del consumo eléctrico ante la temperatura. En sus estudios demuestran que cada región estudiada se comporta de manera diferente. Es decir, para ciertas regiones la sensibilidad a los cambios de temperatura es más alta que en otras regiones, sin embargo, hay casos en los que no hay una relación directa. Esto se debe a que hay otras variables que afectan más que la temperatura, por ejemplo: del día de la semana, día laborable o no laborable [11], [12]. Pardo [11], introduce el índice SVI (Seasonality Variation Index) para indicar la relación entre temperatura y consumo eléctrico a lo largo del año. Este índice se ve influenciado por los cambios de estación. La Fig. 7 muestra que la relación temperatura vs. consumo eléctrico (expresada por el índice SVI) cambia de manera mensual, teniendo su punto más bajo en el mes de agosto, donde es considerado como un periodo de vacaciones, por lo que la demanda del sector industrial tiende a decaer en este mes.

Figura 7: Índice SVI de la demanda eléctrica española 1983-1999 

Análisis de temperatura vs. demanda eléctrica utilizando funciones empíricas ortogonales (EOF)

Para facilitar el análisis de series temporales, y conociéndose que posteriormente en el avance de este proyecto se manejará una gran cantidad de datos. Para el propósito de trabajo se propone el uso funciones Empíricas Ortogonales (EOF) como herramienta de análisis de minería de datos [18].

Dicha técnica es ampliamente utilizada para el análisis de series temporales de temperatura superficial en las corrientes marinas [17] cuyo concepto geométrico se entiende como la observación de la variabilidad de un fenómeno en distintas componentes las cuales son ortogonales entre sí y cuyas proyecciones de amplitud pueden presentar información valiosa para comprender el fenómeno sin utilizar toda las series de tiempo [19]. Una analogía clásica de esta técnica es la presentada en la Fig. 8, en cuya vista lateral del animal a identificarse, se permite discriminar si es un camello o dromedario, lo que no pasaría si vemos al mismo animal en vista frontal [17].

Figura 8: Representación de un objeto desde diferentes perspectivas 

Por otra parte en el ámbito eléctrico se tiene como referencia el uso de las funciones empíricas ortogonales para el tratamiento de información de unidades de medición sincrofasorial PMU, aplicado en la evaluación de la vulnerabilidad del sistema eléctrico de potencia en tiempo real usando tecnología de medición sincrofasorial [18]. En [18] se realiza el tratamiento de la información con EOF para conseguir una reducción en la cantidad de datos y tener una proyección con información valiosa del fenómeno, ya que utiliza una gran cantidad de datos calculados por la PMU como consecuencia de su frecuencia de muestreo que puede llegar hasta 60 muestras por segundo [20] .

ANÁLISIS DE DATOS

Análisis de correlación

De la literatura conocemos que la temperatura y el consumo eléctrico no tienen una relación lineal [10]-[12]. Sin embargo, por la manera como han sido analizado los datos en trabajos previos [12], [13], nos hace pensar que realizar un análisis de correlación lineal nos puede servir como punto de partida. Para el efecto, se realizó el cálculo del coeficiente de correlación de Pearson [21] con los datos capturados en este sistema. Dado que el sistema fue implementado en el mes de abril 2020, se realizó el cálculo en el periodo del 1 de mayo de 2020 al 31 de octubre 2020.

Para efectos del cálculo en el periodo definido anteriormente, se ha tomado el promedio horario de cada variable. La Fig. 9 muestra el coeficiente de correlación de la demanda eléctrica del SNI y la temperatura de algunas ciudades del Ecuador. La selección de las ciudades para este gráfico ha sido aquellas que representan una región geográfica y tienen un coeficiente de correlación alto. La Tabla 2 muestra todas las correlaciones de las ciudades de las cuales se tiene adquisición del valor de temperatura.

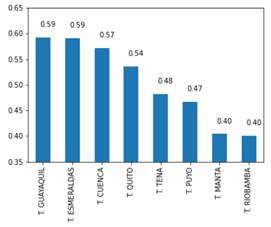
Figura 9: Coeficientes de Correlación de Pearson: Demanda SNI (MW) y Temperaturas (°C) en ciudades del Ecuador 

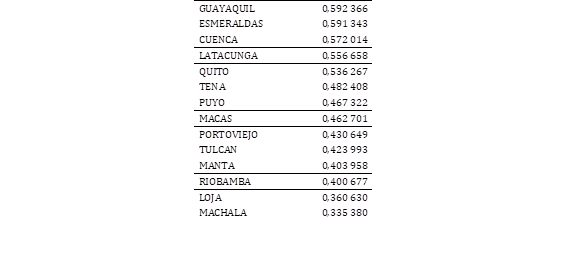
Tabla 2: Coeficiente de correlación de Pearson de temperatura (°C) en cada ciudad vs. la demanda eléctrica (MW) del SNI 

GUAYAQUIL	0,592 366
ESMERALDAS	0,591 343
CUENCA	0,572 014
LATACUNGA	0,556 658
QUITO	0,536 267
TENA	0,482 408
PUYO	0,467 322
MACAS	0,462 701
PORTOVIEJO	0,430 649
TULCAN	0,423 993
MANTA	0,403 958
RIOBAMBA	0,400 677
LOJA	0,360 630
MACHALA	0,335 380

Los resultados sugieren que se analice la relación que existe en la ciudad de Guayaquil y Esmeraldas. Para efectos de este trabajo, se muestra a continuación el gráfico de dispersión de la demanda eléctrica de Guayaquil vs. la temperatura de esta ciudad; procediendo como lo indican los trabajos [10]-[12]. Nótese que no se realiza el gráfico de dispersión contra la demanda del SNI ya que el objetivo de realizar este gráfico es mostrar la relación más cercana entre las dos variables.

Figura 10: Demanda eléctrica de Guayaquil (MW) vs. Temperatura (°C) de la ciudad 

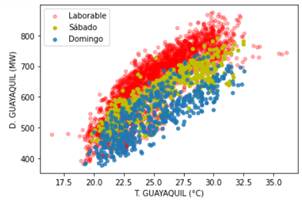
La Fig. 10 muestra la relación de la temperatura y la demanda eléctrica de la ciudad de Guayaquil. Los puntos en color rojo son días laborales (lunes a viernes), los puntos en color amarillo y azul son días no laborables, sábado y domingo respectivamente. Se aprecia que existe una relación lineal positiva por cada subconjunto de datos, esto debido a la característica de consumo eléctrico en días laborales y no laborales.

Continuando con el análisis, se ha procedido a realizar el mismo gráfico de dispersión para la ciudad de Quito. Dado el valor de su coeficiente de correlación (0,54) se espera una relación débil y no lineal; y apoyados en lo descrito en [10]-[12], se puede prever que la influencia de la temperatura en esta ciudad sea menor. La Fig. 11 muestra lo sospechado y nos da más indicios de la relación existente.

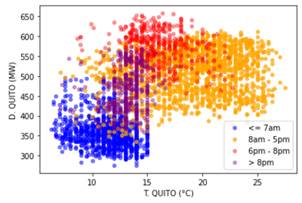
Figura 11: Demanda eléctrica de Quito (MW) vs. Temperatura (°C) de la ciudad, mostrada en diferentes colores para diferentes periodos del día 

Se puede apreciar en la Fig. 11 en puntos de color azul aquellas mediciones comprendidas en el periodo de 0h hasta las 7h, en color naranja de 8h a 17h, en color rojo el periodo de alta demanda de la ciudad, es decir de 18h a 20h, y finalmente el periodo de 21h a 23h en color purpura. Fijándonos en las mediciones de cada grupo por individual, se puede apreciar que es casi nula la correlación entre temperatura y demanda eléctrica. En esta ciudad en particular se concluye que la influencia de temperatura es menor, y que otras variables, como la presencia de luz solar y las costumbres de la ciudad (horarios de trabajo, horarios de encendido de alumbrado público, horas de llegada a domicilios, etc.) influencian de mayor manera en la demanda eléctrica de esta ciudad.

Para atribuir que la influencia de temperatura es mayor en Guayaquil y no depende mucho de sus horarios, como lo ya mostrado en Quito. En la Fig. 12 se muestra el mismo análisis realizado en Quito, pero aplicado a Guayaquil. Del gráfico se concluye que los horarios también influencian en la demanda eléctrica, pero de mayor manera la temperatura.

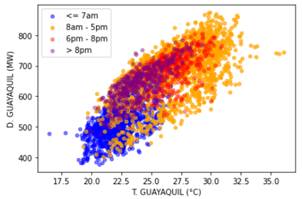
Figura 12: Demanda eléctrica de Guayaquil (MW) vs. Temperatura (°C) de la ciudad, mostrada en diferentes colores para diferentes periodos del día 

Los análisis previos fueron realizados en todas las ciudades enumeradas en la Tabla 2, con resultados similares. Sin embargo, existen ciertas particularidades en cada una de ellas, reflejando así el comportamiento de cada ciudad. Por ejemplo, la Fig. 13 muestra el análisis realizado a la ciudad de Cuenca.

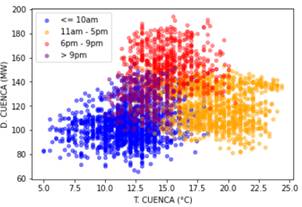
Figura 13: Demanda eléctrica de Cuenca (MW) vs. Temperatura (°C) de la ciudad, mostrada en diferentes colores para diferentes periodos del día 

Se puede notar en la Fig. 13 cierto parecido al de la ciudad de Quito, sin embargo, existen 3 clústeres bastante definidos. El periodo de 0h a 10h caracterizado por una temperatura bajo los 15°C, el periodo de 11h a 17h caracterizado por temperaturas superiores a los 16°C y finalmente el periodo 18h a 21h caracterizado por una alta demanda. Finalmente existe también un clúster no muy bien definido en el centro de los tres anteriormente mencionados correspondiente al periodo de 22h a 23h. Este último análisis demuestra que cada ciudad tiene un comportamiento diferente con respecto a la temperatura. Para las ciudades de la costa y oriente la influencia de temperatura es mayor que para aquellas de la región sierra, donde otras variables explicarían de mejor manera la variabilidad de la demanda.

Análisis de las funciones empíricas ortogonales de la demanda eléctrica y temperatura

Como segundo análisis con el objetivo de observar los fenómenos de demanda y temperatura horaria por 6 meses de análisis. Estas variables (4320 registros cada una) fueron transformadas a través de las funciones empíricas ortogonales para lograr explicar al menos el 99.5 % de la variabilidad del fenómeno. Se aplicó la técnica de minería de datos llamada Funciones Empíricas Ortogonales EOF [17], [18] las cuales se resumen en las Tabla 3 y Tabla 4:

Tabla 3: Resumen de Funciones Empíricas Ortogonales que logran al menos el 99.5% de la variabilidad del de la demanda pmmáxima horaria 

Fenómeno	Numero de EOF	Cantidad de datos
Demanda_UIO	3	72
Demanda_CUE	5	120
Demanda_GYE	3	72

Tabla 4: Resumen de Funciones Empíricas Ortogonales que logran al menos el 99.5% de la variabilidad del de la temperatura máxima horaria 

Fenómeno	Numero de EOF	Cantidad de datos
Temp_UIO	6	144
Temp_CUE	5	120
Temp_GYE	6	72

Con la descomposición de las series temporales en vectores empíricos se aplicó el índice de correlación de Pearson para evaluar cuales son las funciones empíricas ortogonales que explicarían de mejor manera la correlación entre la demanda horaria y la temperatura. Esta correlación está resumida en la Tabla 5. Esta información ganada puede aportar a los modelos de predicción de la demanda eléctrica. Este aporte en los modelos de predicción de la demanda es un tema futuro por realizar, ya que, para ello, se deberá incluir también el análisis realizado en la sección 5.1. Esto debido a que cada ciudad presenta un comportamiento diferente de acuerdo con sus horarios y la sensibilidad a la temperatura cambia dependiendo de la región geográfica de cada ciudad.

Tabla 5: Resumen de Tuplas Funciones Empíricas Ortogonales Demanda Temperatura con mayor correlación  

Ciudad	EOF Dem	EOF Temp	Correlation
Quito	EOF_3	EOF_2	-0,85
Cuenca	EOF_1	EOF_1	0,66
Guayaquil	EOF_1	EOF_1	0,81

Además, en la Tabla 5 se observa que para las ciudades de Quito y Guayaquil existe una correlación muy alta entre la tupla de vectores empíricos ortogonales de temperatura y demanda eléctrica. Para una mejor compresión de esta correlación, se ha graficado la función ortogonal EOF1 de la demanda eléctrica de Guayaquil y la EOF1 de su temperatura, la cual se observa en la Fig. 14.

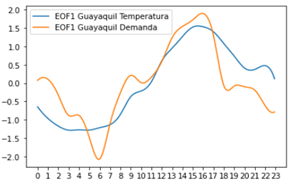
Figura 14: Función ortogonal EOF_1 de la demanda eléctrica de Guayaquil y la EOF_1 de su temperatura 

Para el caso de Guayaquil, esta es positiva mientras que para el caso de Quito esta es negativa. La correlación negativa en Quito queda explicada por la alta demanda eléctrica en condiciones de temperatura baja en el periodo de demanda pico, de 6pm a 8pm, como se aprecia en la Fig. 11. Este comportamiento no ocurre necesariamente en la ciudad de Guayaquil, donde la temperatura sigue alta durante el periodo de demanda pico, véase Fig. 12.

CONCLUSIONES Y RECOMENDACIONES

Con este trabajo se tiene información de las condiciones climáticas que permiten mejorar la conciencia situacional y la toma de decisiones en la operación en tiempo real del S.N.I.

Se demostró que es posible disponer de información en el SCADA/EMS de fuentes como páginas web con información confiable. Esta iniciativa abre la puerta a nuevos desarrollos, en los cuales se necesiten datos de fuentes externas, como aquellas publicadas en servicios web o páginas web confiables.

Para los casos de las ciudades de Guayaquil y Cuenca, se demostró que la función empírica ortogonal representa el 81.5% y 60.1% de la variabilidad de la demanda respectivamente. La correlación de las ciudades de Guayaquil y Cuenca es fuerte y moderada respectivamente, en función de las funciones empíricas ortogonales de temperatura que representan el 67.9% y 72.9% respectivamente. Lo que permitirá utilizar esta metodología para fortalecer los modelos de predicción de demanda eléctrica utilizados actualmente en la planificación del despacho diario.

Para el caso de la ciudad de Quito, el análisis de correlación no es tan aplicable dado que las funciones empíricas ortogonales, EOF_3 de demanda y EOF_2 de temperatura no representan un porcentaje de variabilidad considerable de dichas magnitudes. En consecuencia, se determina que deben existir otras variables que permitan explicar de mejor manera la variabilidad de la demanda, como por ejemplo la presencia de luz solar en el transcurso del día que influye directamente en el alumbrado público de la ciudad.

Dependiendo de la ciudad, se determinó que la correlación de demanda y temperatura es lineal positiva para los casos en que es sensible a la temperatura. Ese fue el caso de algunas de las ciudades de la costa ecuatoriana. Además, se observó que es importante discriminar los días laborables de los no laborables para obtener una mejor correlación. En otras ciudades donde la sensibilidad a la temperatura es menor, se pudo determinar que su correlación es lineal en ciertos periodos de tiempo durante el día.

Se recomienda continuar el acercamiento con el INAMHI para tener una fuente redundante de información y verificar si la nueva fuente de información tiene mejores prestaciones que las que actualmente se tiene de forma gratuita.

Una vez finalizado la captura de datos de forma anual, se recomienda realizar el mismo estudio discriminando la estacionalidad, temporada seca, temporada lluviosa y que permita aportar al modelo de predicción de demanda.