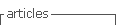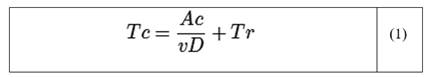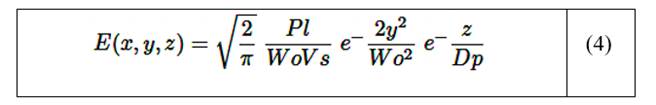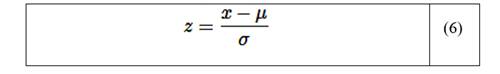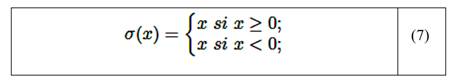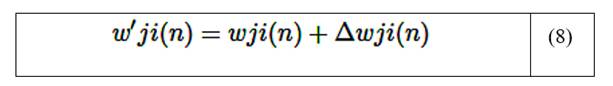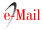Introducción
En los últimos años, las técnicas de fabricación aditiva han experimentado un progreso acelerado en el desarrollo de prototipos y fabricación en diversos campos [1-3]. La impresión de polímeros ha desempeñado un papel clave en este avance debido a que su tecnología está ampliamente disponible para los desarrolladores. La nueva generación de impresoras ha impulsado significativamente la innovación, reduciendo el tiempo y los costos del desarrollo de productos; además, el uso de técnicas de fabricación aditiva en la industria se ha convertido en un campo de gran interés debido a su alto rendimiento y facilidad para fabricar geometrías tridimensionales complejas.
El costo relativamente bajo de las impresoras 3D de diversos tipos, disponibles comercialmente, permite el uso de una amplia gama de materiales con diferentes calidades, precisiones y resoluciones. Entre las tecnologías más comunes se destaca la SLA (estereolitografía), que ofrece varias ventajas en aplicaciones que requieren precisión, como interfaces fáciles de usar, alta resolución y velocidad de impresión relativamente rápida [4-6].
Las propiedades de las piezas impresas con SLA están íntimamente derivadas del proceso de impresión y del posprocesamiento. En los últimos años, se ha estudiado las propiedades mecánicas obtenidas a partir de las piezas impresas con SLA en las diferentes resinas de curado de luz disponibles en el mercado, incluso se ha investigado la mejora de las resinas mediante la evaluación del proceso de curado de luz [7-9]. Se suelen estudiar propiedades como la resistencia a la tracción, el módulo de elasticidad y la resistencia a la compresión [10-12]; sin embargo, la información sobre las propiedades de dureza y desgaste es escasa.
La dureza superficial de los materiales poliméricos es un factor importante en su resistencia al desgaste abrasivo y adhesivo. Un material polimérico con una mayor dureza superficial tendrá una mayor resistencia al desgaste, ya que será menos propenso a la deformación, adhesión y transferencia de material durante el contacto con superficies abrasivas o adhesivas [13]. Sin embargo, también es importante considerar otros factores, como la estructura química del polímero y su resistencia al deslizamiento y deformación, para una comprensión completa de su comportamiento tribológico [14].
Las piezas impresas con SLA se utilizan cada vez más en aplicaciones de ingeniería, donde el fenómeno de desgaste es un aspecto importante para tener en cuenta. Dado que la dureza es una propiedad relacionada con el proceso de desgaste, su inclusión en el análisis también es necesaria. Estudiar la correlación entre desgaste, dureza y parámetros del proceso de impresión SLA es importante para diseñar compuestos adecuados que cumplan con los diversos requisitos especiales.
La predicción de propiedades mecánicas es fundamental en el diseño de piezas y componentes para garantizar su correcto funcionamiento. El uso de redes neuronales artificiales (ANN, por sus siglas en inglés) para predecir propiedades mecánicas de materiales ha demostrado ser una herramienta muy útil y poderosa en la ingeniería, en diferentes campos de la fabricación y específicamente en cuestiones relacionadas con el desgaste [10], [15, 16]. Las ANN pueden aprender patrones complejos y no lineales a partir de grandes conjuntos de datos y, por lo tanto, predecir con precisión las propiedades mecánicas de materiales a partir de información limitada. Esto es especialmente útil cuando no se dispone de datos experimentales sobre las propiedades mecánicas de un material en particular o cuando se desea reducir el tiempo y los costos asociados con las pruebas mecánicas tradicionales. En resumen, el uso de ANN para predecir propiedades mecánicas es una herramienta valiosa que puede ayudar a los ingenieros a diseñar piezas y componentes más eficientes y seguros.
Los enfoques de redes neuronales (NN) son metodologías ampliamente utilizadas que se informan en la literatura entre varias técnicas de aprendizaje automático [17]. La capacidad de las NN artificiales para capturar relaciones complejas entre los datos de entrada y salida es valiosa en procesos de fabricación, donde es difícil y costoso obtener grandes conjuntos de datos experimentales para la modelización del proceso. Además, los modelos de NN muestran una mejora en el error experimental del 40 % al 70 % [18].
Este artículo estudia la predicción del desgaste por abrasión y la dureza obtenida a partir de pruebas experimentales en piezas impresas con resinas termoestables (resinas resistentes y transparentes) utilizando SLA. En este trabajo, en primer lugar, se presenta la recopilación de las propiedades tecnológicas de las resinas impresas y los fundamentos de la impresión; en segundo lugar, se proporciona el análisis de la resistencia a la dureza y al desgaste de la impresión 3D mediante estereolitografía SLA mediante experimentos y, finalmente, el desgaste abrasivo durante el proceso de impresión 3D se estima utilizando una red neuronal artificial basada en los datos experimentales.
Materiales y métodos
En primer lugar, se analizarán los materiales y sus características, a continuación, el diseño experimental, posteriormente el proceso de obtención del material impreso, luego el análisis de desgaste y dureza de los elementos probados y, al final, la predicción mediante redes neuronales artificiales, como se muestra en el diagrama de flujo en la Figura 1.
Materiales
Se utilizaron dos tipos de resinas para la evaluación de propiedades, Clear y Tough de la marca FormlabsTM. La resina Clear FLGPCL04 se utiliza para imprimir materiales con alta resolución y un acabado suave [19], mientras que la resina Tough FLTOTL05 se emplea para prototipos sólidos porque equilibra resistencia y funcionalidad. Tanto el fabricante como las empresas de servicios de impresión recomiendan su uso en elementos que están sometidos a períodos cortos de estrés o fatiga [20], por ejemplo, ensamblajes, configuraciones de tipo prensa y prototipos robustos requieren el uso de la resina mencionada anteriormente.
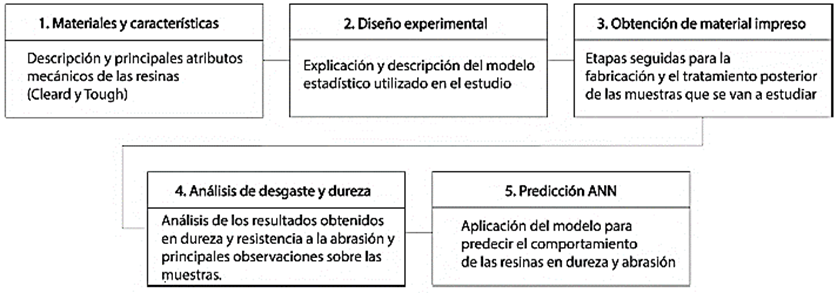
La Tabla 1 resume el comportamiento mecánico del material antes y después del curado, considerando un tiempo de tratamiento de 60 minutos a 60 °C, con una radiación UV de 1,25 mW/cm2 y una longitud de onda de 405 nm para cada tipo de resina. Se proporcionan nueve propiedades para las resinas Clear y Tough; la tabla se divide en tres categorías: curado, sin curar y el método de prueba utilizado para determinar cada propiedad.
Las propiedades mecánicas consideradas incluyen la resistencia última a la tracción, el módulo de elasticidad a tracción, la resistencia a la flexión al 5 % de deformación, la elongación a la rotura, el módulo de elasticidad a flexión, el IZOD entallado, la temperatura de deflexión térmica a 64 Psi y 66 Psi, y la expansión térmica. La evaluación de las propiedades tecnológicas corresponde a las capacidades de absorción de fluidos de las piezas impresas en 3D, como agua, acetona o diésel. La absorción de fluidos es una propiedad importante de los materiales para dispositivos médicos debido a su posible uso como contenedores, conductores de flujo, etc.
La Tabla 2 muestra otras propiedades, como el aumento porcentual de peso de un cubo de 1×1×1 cm, los datos corresponden a las dos resinas en 24 horas de inmersión en diferentes disolventes.
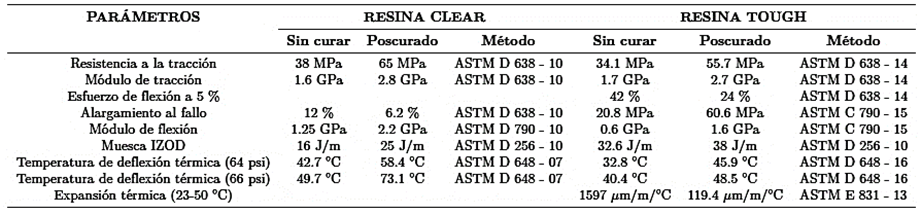
En la Figura 2 se muestra el comportamiento a la tracción de las dos resinas, considerando diferentes tiempos de curado. Debido a su buen comportamiento a la tracción, ambas resinas pueden usarse para imprimir piezas mecánicas. Por ejemplo, la resina Tough se utiliza para imprimir engranajes para prototipos de RC [22], por otro lado, la resina Clear, gracias a su alta calidad superficial, ofrece la posibilidad de ser empleada en elementos visualmente expuestos. Además, la sustitución en cualquier dispositivo es más fácil, ya que los elementos afectados pueden reemplazarse en poco tiempo con uno nuevo gracias a esta tecnología de impresión.
Tabla 2 Ganancia de peso porcentual de las dos resinas en 24 horas de inmersión en diferentes fluidos de un cubo de 1×1×1 cm [20, 21]
Diseño experimental
La matriz ortogonal, en el contexto de un estudio estadístico, es una herramienta utilizada para estudiar y analizar todas las variables de manera independiente y simultánea. Permite que el análisis de una variable no se vea afectado por las otras variables, facilitando el estudio de cada variable por separado y comprendiendo su impacto individual. Esto se debe a la independencia de los datos.
Al analizar variables de manera independiente, se reduce la posibilidad de introducir sesgos o confusiones entre ellas. Esto ayuda a obtener resultados más confiables y precisos porque cada variable se examina de manera aislada y se pueden identificar y controlar mejor posibles fuentes de error.
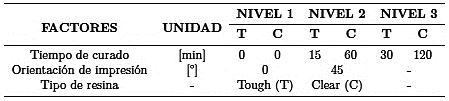
En consecuencia, se aplicó un diseño experimental de matriz ortogonal en el que se utilizaron dos variables cuantitativas (tiempo de curado y orientación de la impresión) y una variable cualitativa correspondiente al tipo de resina con tres niveles, como se presenta en la Tabla 3.
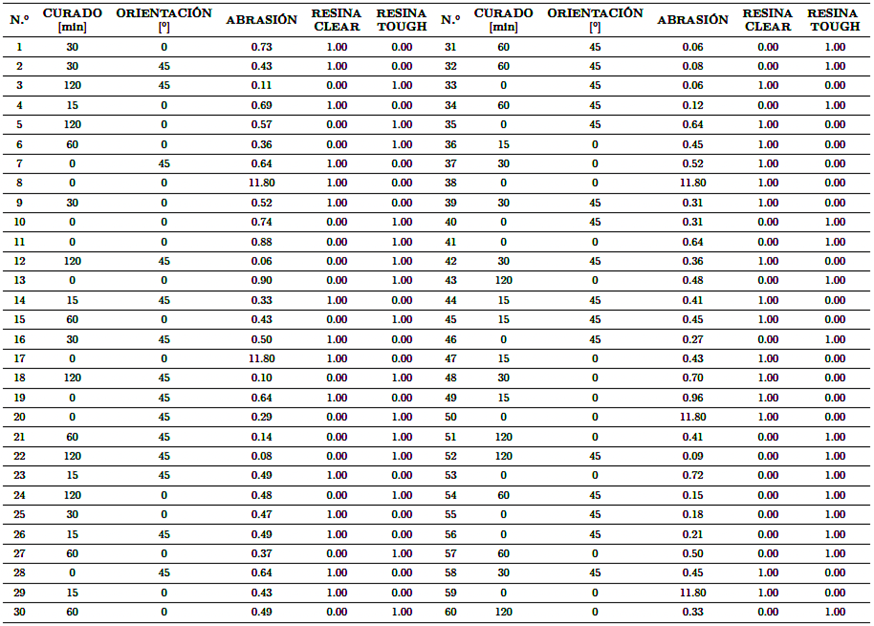
En este análisis, se utilizó una distribución de los datos a partir de un modelo factorial completo. El número de ejecuciones experimentales se fijó en 5, obteniendo así cien combinaciones de datos experimentales. Se realizó una limpieza de los datos en busca de valores nulos, especialmente para la resina Tough con tiempos de curado de 15 y 30 minutos, y la resina Clear con tiempos de curado de 60 y 120 minutos.
Proceso de obtención del material impreso
La Figura 3 muestra un diagrama SIPOC del proceso llevado a cabo para la impresión de las muestras con el material propuesto para el análisis. El gráfico detalla los pasos (1) al (5) que corresponden a las entradas y la creación de prototipos, mientras que el paso (6) detalla las pruebas que se llevaron a cabo para el análisis y la recopilación de datos que alimentaron la red neuronal.
Inicialmente, las resinas se encuentran en estado líquido, almacenadas y suministradas desde cartuchos (1). Luego, las muestras fueron modeladas utilizando software de diseño (2). Para la impresión, se siguieron los parámetros especificados por el fabricante [23] y se configuraron las variables descritas en el diseño experimental (3).
La fabricación de cada muestra a partir del proceso SLA se llevó a cabo mediante la fase de impresión en la máquina Form 2 SLA, siguiendo las pautas del diseño experimental. La fase de lavado se realizó en el equipo Form Wash con solvente de alcohol isopropílico durante un período de 10 a 20 minutos (4) y, finalmente, el curado se llevó a cabo en el equipo Form Cure.
Para la etapa de curado de las muestras, se consideró un intervalo de tiempo de 0 a 30 minutos para la resina Clear y de 0 a 120 minutos para la resina Tough, según se especifica en la Tabla 3 (5). Se puede obtener una estimación del tiempo que se puede emplear por capa a partir de la Ecuación (1). El tiempo de formación (Tc) depende del área de la capa a formar (Ac), la velocidad (v) y el diámetro (D) del haz, más el tiempo de reposicionamiento para la materialización de la capa (Tr). La suma del tiempo de formación de cada capa proporciona el tiempo total de procesamiento [24].
En términos generales, el proceso de impresión 3D SLA puede definirse matemáticamente mediante relaciones como la profundidad de curado, el ancho de la línea de curado y la exposición láser en cualquier punto.
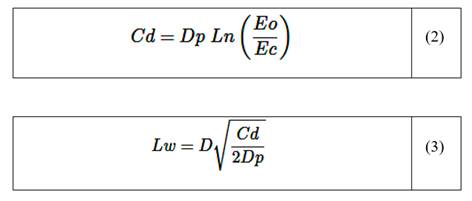
La relación de profundidad de curado (ecuación (2)) está relacionada con la profundidad de penetración láser (Dp), la energía de exposición en la superficie de la resina (Eo) y la energía mínima para gelificar la resina (Ec) [24]. El ancho de la línea curada (Lw) se expresa mediante la ecuación (3). En esta relación, D es equivalente al diámetro del láser utilizado en la máquina de impresión.
Teniendo en cuenta que el láser tiene movimientos en los tres ejes (X - Y - Z), la exposición láser en cualquier punto (E (x, y, z)) se determina mediante la ecuación (4). El punto (x, y) representa la distancia desde el centro hasta el haz, (z) la profundidad en la que se encuentra, (Pl) es igual a la potencia del láser, la anchura media gaussiana (Wo) vs. la velocidad de escaneo del láser y (Dp) la profundidad de penetración del láser [25].
La isotropía es una característica crítica que se relaciona con los parámetros definidos por las ecuaciones 1-4. La isotropía es una de las consecuencias del poscurado, que fortalece las uniones mediante la formación de enlaces covalentes. A nivel microscópico, no hay una diferencia marcada entre las moléculas dispuestas en los planos X - Y - Z. Esto hace que su rendimiento mecánico sea predecible y, por lo tanto, mejor que otros tipos de impresión 3D. Por otro lado, la impermeabilidad es otra característica que mejora el material después del curado, esta característica distintiva es una de las razones por las cuales este tipo de impresión se utiliza a menudo cuando se trabaja con fluidos.
Análisis de desgaste y dureza de los elementos probados
Siguiendo las indicaciones establecidas en la norma ISO 9352. Se aplicó una carga de 1000 gramos y 1000 ciclos a una velocidad de 72 rpm. El tipo de rueda abrasiva utilizada fue de grado intermedio H22. El resultado informado es el índice de desgaste de Taber (TWI), (ecuación (5)), donde A es el peso de la muestra antes de la prueba, B es el peso de la muestra después de la prueba y C es igual al número de ciclos utilizados en la prueba.
Cada espécimen de prueba fue evaluado, y los resultados se expresan en términos de una unidad de dureza Shore D, que representa la resistencia del material a la penetración por la aguja de prueba. En la escala Shore D, valores de dureza más bajos corresponden a materiales más blandos y valores más altos corresponden a materiales más duros. La escala Shore D es particularmente adecuada para materiales rígidos, con un rango típico de dureza de 20 a 90 Shore D.
Métodos de análisis de redes neuronales artificiales (ANN)
Una red neuronal es una técnica inspirada en el sistema nervioso biológico, que tiene como objetivo replicar la forma en que los humanos aprenden a resolver una amplia variedad de problemas científicos complejos. Las redes neuronales constan de varias capas de neuronas conectadas con pesos sinápticos para simular el cerebro humano. Una red simplificada consta de una capa de entrada con un número de neuronas que depende de las variables de entrada (3 en este estudio), seguida de una o más capas ocultas que transforman esas variables para su uso final en la capa de salida [26, 27].
El sobreajuste es un problema relacionado con el entrenamiento de redes neuronales. Según la investigación [28-30], determina que muy pocas neuronas llevan a un ajuste insuficiente, mientras que un exceso de neuronas puede contribuir al sobreajuste.
La Figura 4 muestra el esquema neuronal utilizado, donde W es el peso sináptico de cada neurona a otra neurona en la siguiente capa.
La arquitectura de la red de alimentación hacia adelante utilizada en este estudio consta de tres neuronas para la capa de entrada, que están ordenadas según el número de variables de entrada. Una neurona está en la capa de salida (desgaste abrasivo) y dos están en capas ocultas con noventa y seis neuronas cada una. El número seleccionado de neuronas en la capa oculta se determina mediante un procedimiento de prueba y error. Para disminuir la dificultad del entrenamiento y equilibrar la importancia de cada parámetro durante el proceso de entrenamiento, la base de datos experimental se normalizó entre los valores 0 y 1.
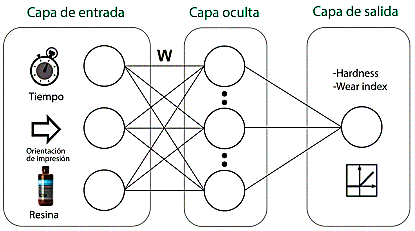
Figura 4 Arquitectura de la red neuronal con tres capas implementadas desde la capa de entrada hasta la capa de salida
La escala de las variables de entrada y salida en el intervalo se determina por la proporción de la diferencia de los datos de entrada y salida respecto a la media y la desviación estándar (ecuación (6)), donde x es un punto de datos, μ es la media y σ es la desviación estándar.
La salida de cada neurona de las capas ocultas y de salida se obtiene mediante la función ReLU. Esta función representa la fusión de activación (ecuación (7)). Se utilizó el algoritmo de optimización de Adam junto con el algoritmo de entrenamiento de retropropagación [31] para entrenar la red neuronal multicapa y calcular el gradiente necesario para el ajuste de pesos.
La fase de entrenamiento de la ANN determina los pesos de conexión necesarios para dar la respuesta deseada. El primer paso es asignar valores de peso aleatorios a todos los enlaces entre neuronas. A continuación, los valores de parámetros del k-ésimo experimento de la lista de datos de entrenamiento se pasan a través de la red. El valor estimado se compara con el valor deseado utilizando las funciones: error cuadrático medio (MSE) y error absoluto medio (MAE).
Los diferentes pesos que conectan los elementos en la red neuronal se ajustan y se acercan al valor de salida objetivo. La ecuación (8) representa la actualización de los pesos sinápticos, basada en el error calculado en cada neurona.
Donde w′ji(n) representan los pesos ajustados, wji(n) son los pesos anteriores y Δwji(n) es la corrección de peso sináptico. Después de actualizar todos los pesos de acuerdo con el error de entrenamiento, se completa una época (n). Una época es cuando se evalúan todas las pruebas de entrenamiento (60 para este estudio). Si el MSE no es menor que un objetivo específico, el proceso se repite mediante la actualización de los pesos y el aumento del número de épocas requeridas hasta alcanzar el objetivo.
Resultados y discusión
Los resultados se informan en dos etapas, (1) análisis experimental de factores influyentes en las variables de salida (índice de desgaste de Taber y dureza) y (2) predicción de desgaste mediante redes neuronales.
Análisis experimental de variables de salida
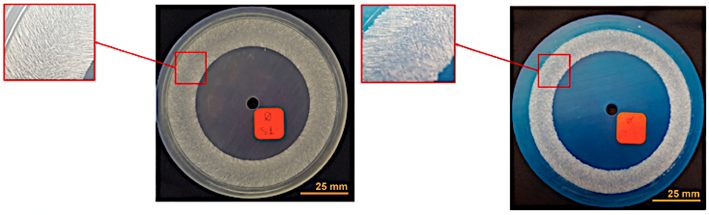
La Figura 5 detalla las muestras sometidas a la prueba de abrasión, donde la topología de las muestras ha experimentado un cambio notable. La principal evidencia se muestra en la calidad de la pista dejada por la rueda abrasiva. Esto es consistente con los resultados presentados, que indican que hay una diferencia del 70% en la pérdida de masa entre las muestras blancas (resina Clear) y azules (resina Tough). Siendo estas últimas las más resistentes a la abrasión.
Por otro lado, en cuanto a la prueba de dureza, se puede decir que la escala de dureza de las resinas aumenta a medida que aumenta el tiempo de curado. En otras palabras, hay una relación directamente proporcional. La resina Clear presenta su pico máximo de dureza Shore D a los 15 minutos de curado, con un promedio de 88,4, siendo la más alta entre las dos resinas utilizadas en el estudio. La resina Tough presenta su pico máximo a los 60 minutos de curado con una escala de dureza promedio de 78,6. La Tabla 4 muestra la distribución de los datos de un modelo factorial completo.
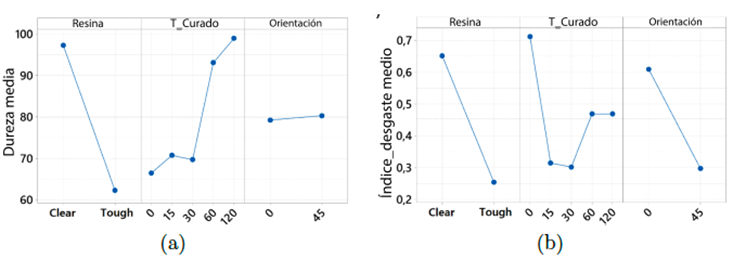
La Figura 6 muestra los resultados experimentales para los efectos principales de la dureza y la tasa de desgaste con un nivel de significancia del 5 %. Para la dureza (Figura 6a), se observa que tanto el tipo de resina como el tiempo de curado son variables incidentes (valor p < 0,01 para los dos factores en el análisis de ANOVA). La orientación de la impresión no es incidente (valor p > 0,01). Por otro lado, la figura 6b muestra que todos los factores (tipo de resina, tiempo de curado y orientación de la impresión) son incidentes en la resistencia a la abrasión (valor p < 0,01) para todos los factores. Para ambas variables de respuesta, la resina con el mejor rendimiento es la resina Clear.
La Figura 7 muestra el comportamiento de la dureza de las dos resinas (Clear, Resina Tough) en función del tiempo de curado; (Figura 7a), correspondiente a la resina Clear, muestra una dureza más alta. Sin embargo, los valores más altos se encuentran en el rango de 15 a 30 minutos. Por otro lado, se observa un comportamiento similar en la resina Tough (Figura 7b), donde es evidente que cuanto más largo es el tiempo de curado, mayor es la dureza. Para lograr estos resultados, es necesario un rango de curado de 60 minutos. También se observa que no se debe exceder el tiempo de curado recomendado, ya que no mejora la dureza del material.
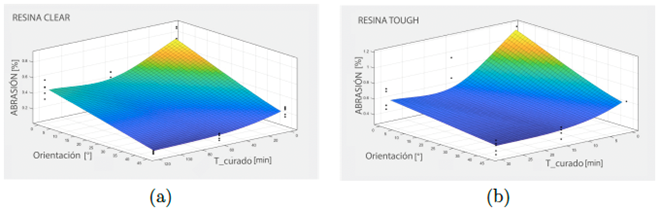
La Figura 8 muestra los resultados de la abrasión. Las dos resinas tienen un patrón de comportamiento distinto. Al no estar curadas, no muestran una buena estabilidad (baja resistencia). La resistencia a la abrasión aumenta cuando las dos resinas se curan por primera vez. Independientemente del tiempo, se observa que el cambio es notable entre 0 min y 5 min (Resina Clear 8a). Posteriormente, como muestran los resultados de la resistencia a la tracción, los valores no muestran cambios notables. En otras palabras, cuanto más largo es el tiempo de curado, mayor es la resistencia a la abrasión.
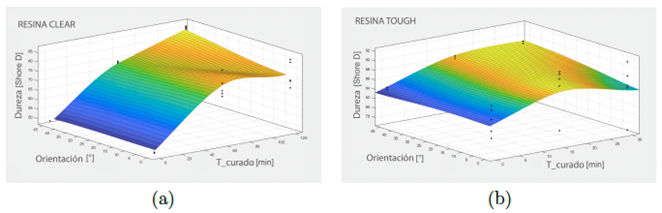
Figura 7 Resultados experimentales. (a) Resina Clear: Dureza vs. Orientación vs. Poscurado (b) Resina Tough: Dureza vs. Tiempo de poscurado vs. Orientación
Predicción del desgaste abrasivo y dureza mediante redes neuronales artificiales
Se desarrolló un modelo neuronal para estimar la tasa de desgaste de Taber (TDI) y la dureza basándose en diferentes combinaciones de impresión 3D estereolitográfica. La base de datos se obtuvo mediante pruebas de laboratorio. Los datos experimentales utilizados para la etapa de entrenamiento se dividieron por validación cruzada en un 80 % para el entrenamiento y un 20 % para la validación. Se desarrolló con un esquema neuronal de alimentación directa y retropropagación en un total de 60 datos experimentales.
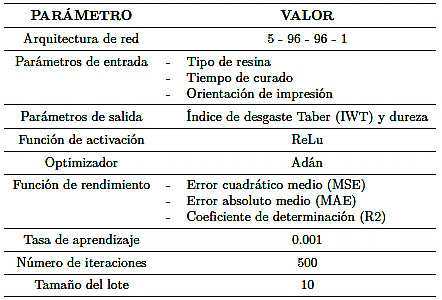
El modelo de mejor rendimiento fue la arquitectura 5-96-96-1. La función de activación ReLu se utilizó tanto para las capas ocultas como para la capa de salida. La Figura 9 muestra la relación entre los valores obtenidos mediante el entrenamiento neuronal y los valores obtenidos experimentalmente.
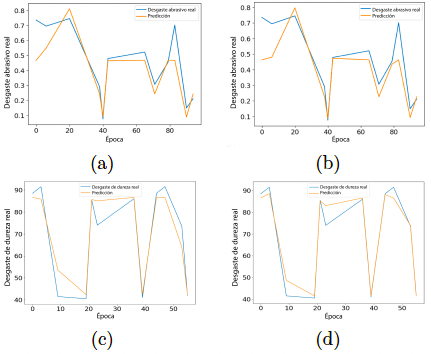
Figura 9 Comparación general entre los valores predichos y experimentales del desgaste abrasivo. a) Desgaste abrasivo con resina Clear b) Desgaste abrasivo con resina Tough c) Dureza con resina Clear d) Dureza con resina Tough.
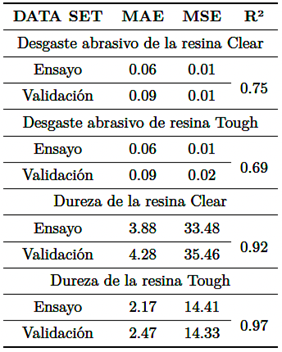
Se presenta la evolución del MAE y MSE con las épocas para la red neuronal diseñada en la Figura 10, donde se observa la convergencia de los resultados. El MAE al final del procedimiento de entrenamiento del desgaste abrasivo resultó ser 0,09 utilizando resina Clear y un valor de MSE de 0,01. Para medir la precisión de la ANN, se calculó el coeficiente de correlación (R2) entre los resultados y los objetivos. En este caso, R2 = 0,75 representa una correlación entre los valores experimentales y estimados. El MAE es 2,47 utilizando resina Tough y un valor de MSE de 14,3. El coeficiente de correlación (R2) entre los resultados y los objetivos fue calculado. En este caso, R2 = 0,97.
MAE evaluó el rendimiento predictivo del modelo, así como los valores de MSE y R2. Investigaciones anteriores [26], [32], [33] recomiendan que el modelo debe tener un R2 alto y un MAE y MSE bajos para que el modelo neuronal tenga una eficiencia alta. La Figura 11 muestra los resultados del proceso de entrenamiento de la ANN después de alcanzar el gradiente mínimo. La Tabla 5 presenta los resultados de MAE y MSE después del entrenamiento de la red.
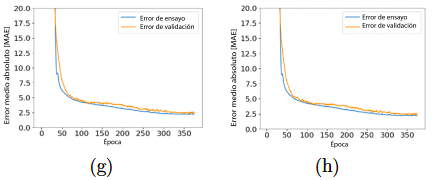

Figura 10 Evolución del error absoluto medio y evolución del error cuadrático medio con el número de los tiempos. a) MAE del desgaste abrasivo con resina Clear b) MSE del desgaste abrasivo con resina Clear c) MAE del desgaste abrasivo con resina Tough d) MSE del desgaste abrasivo con resina Tough e) MAE de la dureza con resina Clear f) MSE de la dureza con resina Clear g) MAE de la dureza con resina Tough h) MSE de la dureza con resina Tough.
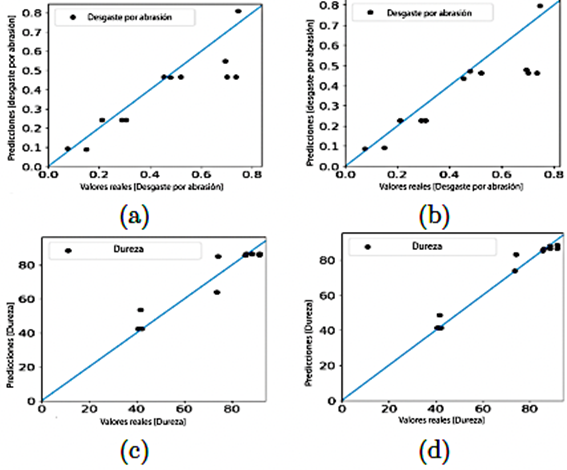
Figura 11 Regresión entre los datos presentados por la red neuronal y los valores reales obtenidos experimentalmente para el desgaste abrasivo. a) Desgaste abrasivo con resina Clear b) Desgaste abrasivo con resina Tough c) Dureza con resina Clear d) Dureza con resina Tough
La Tabla 6 presenta la mejor configuración de hiperparámetros para el modelo neuronal, considerando los resultados estadísticos y el costo computacional.
La Figura 12 ilustra la distribución de los residuos del modelo. La mayoría de los residuos están cerca de cero, lo que determina el rendimiento satisfactorio del modelo propuesto de red neuronal. Los residuos no están cerca de una curva normal. Este comportamiento puede deberse al tamaño de muestra pequeño considerado para el entrenamiento.
La Tabla 7 muestra el error porcentual presentado por la red en cada conjunto de datos de validación. Los resultados indican similitudes entre los estudios experimentales y el modelo neuronal, respaldando la confiabilidad del modelo.
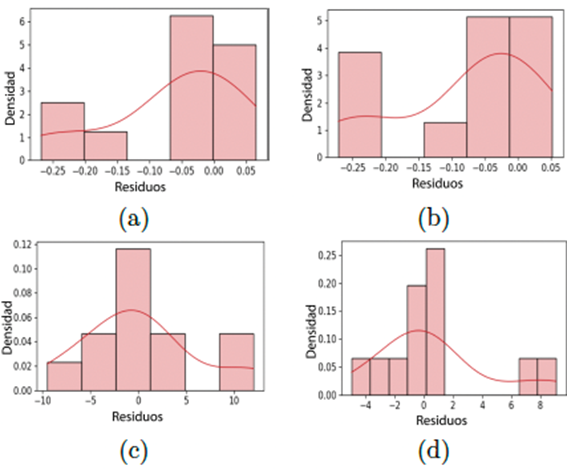
Figura 12 a) Desgaste abrasivo con resina transparente b) Desgaste abrasivo con resina resistente c) Dureza con resina transparente d) Dureza con resina resistente. Nota: El gráfico de distribución de residuos tiende a una curva gaussiana, es decir, la mayoría de los residuos tienden a acercarse al valor de cero.
Conclusiones
El primer objetivo está relacionado con el análisis de las propiedades mecánicas de las resinas; se determinó que la dureza y la resistencia aumentan en función del tiempo de poscurado de cada resina. Las resinas Tough y Clear han mostrado un patrón definido en su comportamiento, especialmente en dureza y abrasión. Cuando no están curadas, sus propiedades son inferiores que cuando se curan a 60 minutos, lo cual está en línea con las recomendaciones del fabricante. Este salto es muy notable, especialmente en dureza y resistencia a la tracción. Si se aumenta el tiempo de curado, sus propiedades tienen un aumento insignificante. Después del tiempo máximo de curado de 120 minutos, no habrá una mejora apreciable en las propiedades.
El modelo de red neuronal predijo con éxito los resultados experimentales, con un error cuadrático medio de 0,014 y un error absoluto medio de 0,085, utilizando resina transparente. El EAM es de 2,27 utilizando resina resistente, con un valor de ECM de 14,33. El coeficiente de correlación (R2) entre los resultados y los objetivos fue calculado. En este caso, R2 = 0,97. Esto muestra que los resultados predichos concuerdan con los valores medidos. También se verifica que el modelo de red neuronal artificial es confiable y que los resultados predichos proporcionan información útil para desarrollar nuevos materiales resistentes al desgaste abrasivo.
Los diagramas visuales de superficie construidos con los resultados de la red pueden utilizarse para monitorizar el impacto de la evolución del desgaste, reducir daños y prevenir la fractura de componentes. En última instancia, se concluye que la impresión 3D con tecnología SLA utilizando resinas transparentes y resistentes son buenas alternativas para la fabricación de componentes emergentes debido a su dureza y buen comportamiento frente al desgaste abrasivo.
El experimento de abrasión se limita a un grado medio debido al uso de muelas abrasivas del tipo mencionado anteriormente. Dado que existe un grado específico de abrasión, las condiciones experimentales se limitan a las propuestas por la norma de abrasión ISO 9352. Si es necesario conocer el comportamiento del material bajo condiciones de alta y baja abrasión, se recomienda realizar experimentos utilizando muelas abrasivas que cumplan con los requisitos correspondientes.