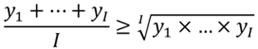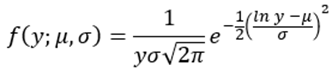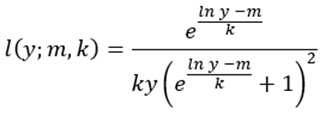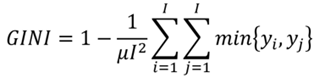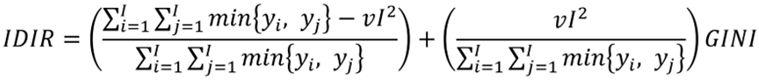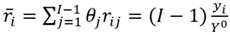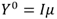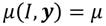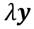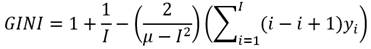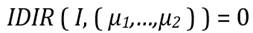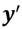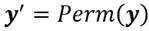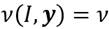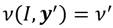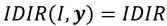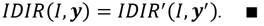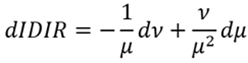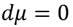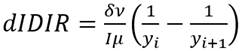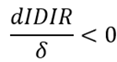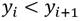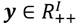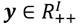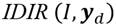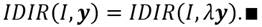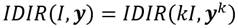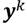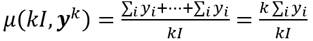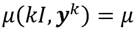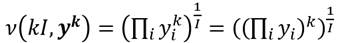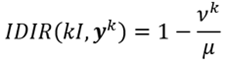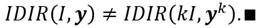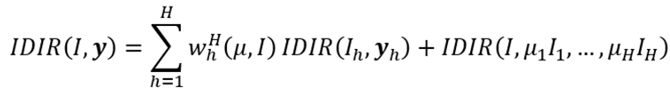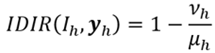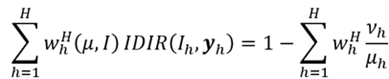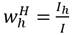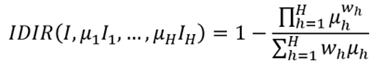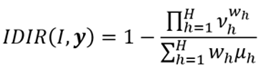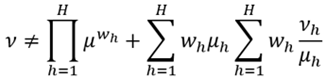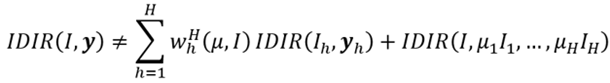Introducción
Existen diversas clases de índices que miden la desigualdad económica de los ingresos. Una clasificación general tipifica algunas de estas mediciones como medidas positivas y otras como medidas normativas. Las primeras basadas únicamente en medidas estadísticas mientras que las segundas están fundamentadas en el marco informacional de alguna función de bienestar social (Villar, 2017). También, los índices se pueden clasificar según el enfoque de la dimensión o del indicador, manteniendo constante estos o no (Subramanian, 2004). Entre todas las medidas, la de mayor uso en el campo de la economía, específicamente en los campos de la economía del bienestar y de la teoría del desarrollo económico, es el coeficiente de Gini. Sin embargo, este índice supone una curva Lorenz, siendo entonces posible que para dos curvas de Lorenz diferentes podemos obtener el mismo coeficiente de Gini (Medina, 2001).
El problema de la dominancia estocástica de una curva de Lorenz sobre otra, y su relación con el índice de Gini, motivó el inicio del presente trabajo, en el cual proponemos un índice fundamentado en la teoría del bienestar social, específicamente en la función de bienestar de Nash generalizada (Nash, 1950).1 Si bien el fundamento es normativo, el índice propuesto se desarrolla sobre la base de medidas estadísticas (enfoque positivo) superando así esta dicotomía de la clasificación de las medidas de desigualdad. Realizaremos algunos cálculos del índice basado en situaciones distributivas simuladas, la primera con una distribución de Pareto, la segunda según una distribución log normal y por último con una distribución log logística. Asimismo, a lo largo de las simulaciones compararemos la performance de los resultados del índice propuesto con los resultados del índice de Gini.2 Finalmente, realizaremos una estimación del índice para los departamentos del Perú, para el periodo 2004 - 2017.
Revisión de la Literatura
En la literatura sobre índices de la desigualdad distributiva de ingresos o riquezas se encuentra la relación media geométrica - media aritmética únicamente como un caso particular de la medida de la desigualdad llamado índice de Atkinson, cuando el parámetro 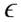 , que representa la aversión a la desigualdad, es igual a uno, esto es
, que representa la aversión a la desigualdad, es igual a uno, esto es 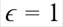 (Allison, 1978). Desde otro punto de vista, el estadístico - matemático, la expresión de una medida de la desigualdad distributiva de ingresos, en términos de la varianza logarítmica o de la varianza de los logaritmos, estas difieren en el caso de la primera, en la utilización de la media aritmética, y en la segunda en el uso de la media geométrica de los ingresos (Atuesta et al., 2018). El uso de la primera medida es más común, sin embargo, la segunda medida sería una medida más adecuada cuando se quiera estudiar el efecto de las transferencias de ingreso sobre los cuartiles inferiores. Adicionalmente, el uso de los logaritmos tiende a disminuir la desviación destacando las diferencias en el extremo inferior de la distribución de ingresos, dificultando su uso como una medida del bienestar social, pues su expresión
(Allison, 1978). Desde otro punto de vista, el estadístico - matemático, la expresión de una medida de la desigualdad distributiva de ingresos, en términos de la varianza logarítmica o de la varianza de los logaritmos, estas difieren en el caso de la primera, en la utilización de la media aritmética, y en la segunda en el uso de la media geométrica de los ingresos (Atuesta et al., 2018). El uso de la primera medida es más común, sin embargo, la segunda medida sería una medida más adecuada cuando se quiera estudiar el efecto de las transferencias de ingreso sobre los cuartiles inferiores. Adicionalmente, el uso de los logaritmos tiende a disminuir la desviación destacando las diferencias en el extremo inferior de la distribución de ingresos, dificultando su uso como una medida del bienestar social, pues su expresión  ya no será cóncava para los niveles de ingreso mayores (Sen & Foster, 1997).
ya no será cóncava para los niveles de ingreso mayores (Sen & Foster, 1997).
Entonces, tanto la medida media aritmética - media geométrica que se deriva como un caso especial del índice de Atkinson como la propuesta estadística-matemática que recoge los efectos de las transferencias, carecen del sustento de un marco teórico normativo basado en una teoría del bienestar social. No poseen una teoría del bienestar que fundamente el uso de ambas medidas estadísticas para medir la desigualdad y que dé cuenta de la relación entre desigualdad y bienestar social. Por otro lado, en el marco de una teoría de la justicia distributiva, se encuentra una evaluación, por un lado, del sentimiento de justicia de los recursos individuales en relación con la población relevante; tratándose este aspecto como el logaritmo de la razón de la media geométrica de la distribución del bien a la media aritmética de la distribución del bien de valor; mostrándose una relación entre este ratio como medida de la desigualdad y el sentido de justicia distributiva (Jasso, 1980). Este planteamiento, si bien posee una teoría de la justicia subyacente, no existe una teoría de bienestar social explícita.
Finalmente, Jasso (1982), en una propuesta más acabada y posterior, propone la construcción de una medida de la desigualdad basada en los dos estadísticos mencionados, sosteniendo que la proporción de cantidad que se siente injustamente mal recompensada es igual a la proporción de una cantidad de ingresos por debajo de la media, donde la justicia media viene dada por 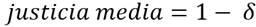 , siendo
, siendo 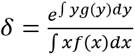 para y = log x. Esto es, el ratio media aritmética - media geométrica. Así, se presenta la relación justicia media = log desigualdad de ingresos, donde la desigualdad distributiva de ingresos es medida por el ratio ingreso medio aritmética - ingreso medio geométrico. Esta formulación coincide con nuestra formulación, sin embargo; nuevamente, no se formula una relación explícita entre la desigualdad distributiva y el bienestar social.
para y = log x. Esto es, el ratio media aritmética - media geométrica. Así, se presenta la relación justicia media = log desigualdad de ingresos, donde la desigualdad distributiva de ingresos es medida por el ratio ingreso medio aritmética - ingreso medio geométrico. Esta formulación coincide con nuestra formulación, sin embargo; nuevamente, no se formula una relación explícita entre la desigualdad distributiva y el bienestar social.
Marco analítico
Se supondrá una sociedad compuesta por un conjunto, 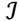 , de receptores de ingresos, donde
, de receptores de ingresos, donde 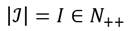 .3 El ingreso de cada receptor
.3 El ingreso de cada receptor 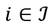 viene dado por
viene dado por 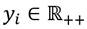 .4 Una distribución de ingreso dada se denota por el vector
.4 Una distribución de ingreso dada se denota por el vector 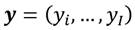 , donde el subíndice no sólo representa al receptor sino además representa una indización de tal forma que
, donde el subíndice no sólo representa al receptor sino además representa una indización de tal forma que 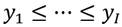 . El espacio de distribución de ingresos se denota por el conjunto
. El espacio de distribución de ingresos se denota por el conjunto 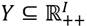 . Luego, cada individuo miembro de la sociedad
. Luego, cada individuo miembro de la sociedad 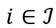 posee preferencias regulares representadas por una función de utilidad
posee preferencias regulares representadas por una función de utilidad 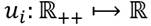 , donde
, donde 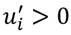 y
y 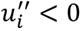 (Arrow, 1971). Entonces, para una distribución dada,
(Arrow, 1971). Entonces, para una distribución dada, 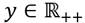 , el ingreso medio aritmético viene dado por la función
, el ingreso medio aritmético viene dado por la función 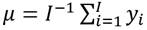 y la proporción de ingreso del receptor i en relación a la renta total viene dada por el parámetro
y la proporción de ingreso del receptor i en relación a la renta total viene dada por el parámetro 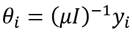 .
.
La función de bienestar de Nash
El criterio de Nash generalizado (Maskin, 1976; Weymark, 2016), permite formular un funcional de bienestar social bajo un marco informacional de representación cardinal y de comparabilidad de variaciones de utilidad. Formalmente,
donde 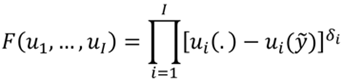 y
y  es el ingreso correspondiente a un estado social de statu quo.
es el ingreso correspondiente a un estado social de statu quo.
Para efectos de la construcción de la medida de la desigualdad que se propone supondremos que  para todo
para todo  . Además, específicamente, la función de utilidad individual es bien comportada y de forma
. Además, específicamente, la función de utilidad individual es bien comportada y de forma 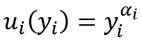 , donde
, donde 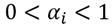 .5 Además, asumiremos que para todo receptor
.5 Además, asumiremos que para todo receptor 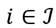 ocurre
ocurre 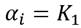 y
y 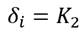 , siendo
, siendo 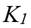 y
y 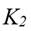 constantes.6 Luego, por simplicidad suponemos que
constantes.6 Luego, por simplicidad suponemos que 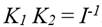 . Así, la funcional específica a desarrollar será:
. Así, la funcional específica a desarrollar será:
donde v es el ingreso medio geométrico.
En consecuencia, para una distribución de ingresos dada 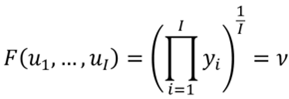 el bienestar efectivo, según la ecuación (2) vendría dado por la media geométrica
el bienestar efectivo, según la ecuación (2) vendría dado por la media geométrica 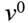 . Tenemos así, una medida estadística descriptiva que no sólo sería una aproximación del bienestar efectivo sino que además es una medida monetaria del bienestar.
. Tenemos así, una medida estadística descriptiva que no sólo sería una aproximación del bienestar efectivo sino que además es una medida monetaria del bienestar.
En cuanto al bienestar social máximo, se considerará que para la sociedad de I receptores con un ingreso total igual a 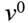 , la distribución de ingreso que maximiza el bienestar social es
, la distribución de ingreso que maximiza el bienestar social es 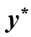 , donde esta distribución es el resultado de resolver el problema siguiente,
, donde esta distribución es el resultado de resolver el problema siguiente,
de este programa se obtiene una asignación de ingresos igualitaria. Esto es, un resultado socialmente óptimo donde 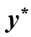 .7 Por tanto, la distribución de ingresos que maximiza el bienestar social será
.7 Por tanto, la distribución de ingresos que maximiza el bienestar social será 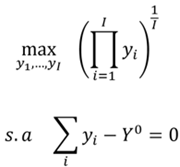 . Así, el máximo bienestar social estará asociado con la medida estadística de la media aritmética:
. Así, el máximo bienestar social estará asociado con la medida estadística de la media aritmética:
Y nuevamente, se tendrá otra medida estadística como una medida monetaria del bienestar social óptimo.
El ingreso relativo
Nuevamente, sea la sociedad conformada por un número de I receptores de ingresos. Para cada distribución de ingresos 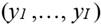 que agota el ingreso total
que agota el ingreso total 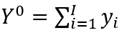 , se tiene que cada receptor posee como ambiente un vector de ingresos relativos. Para el i-ésimo receptor este es,
, se tiene que cada receptor posee como ambiente un vector de ingresos relativos. Para el i-ésimo receptor este es, 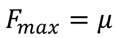 , donde
, donde 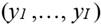 ,
, 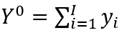 .
.
Con la intención de resaltar el mayor grado de desigualdad del i-ésimo receptor en relación a los receptores que tienen mayores ingresos, en el cálculo del ingreso relativo promedio, al ingreso relativo 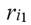 se le asignará un menor peso que al ingreso relativo
se le asignará un menor peso que al ingreso relativo 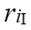 , ya que
, ya que 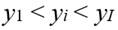 . La ponderación tomará en cuenta la importancia del ingreso del j-ésimo receptor opositor en relación al ingreso total
. La ponderación tomará en cuenta la importancia del ingreso del j-ésimo receptor opositor en relación al ingreso total 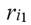 a distribuir entre todos los receptores. Por tanto,
a distribuir entre todos los receptores. Por tanto, 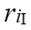 , donde
, donde 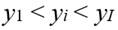 .
.
En seguida, para cada receptor 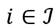 , el ingreso relativo que tomaremos como referencia será su ingreso relativo promedio que es igual al promedio aritmético ponderado
, el ingreso relativo que tomaremos como referencia será su ingreso relativo promedio que es igual al promedio aritmético ponderado 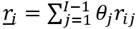 , donde
, donde 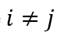 y
y 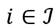 . Luego, simplificando algebraicamente obtendremos el siguiente resultado como una expresión del ingreso relativo promedio por receptor:8
. Luego, simplificando algebraicamente obtendremos el siguiente resultado como una expresión del ingreso relativo promedio por receptor:8
A nivel agregado, para toda la sociedad, en la cual existen I receptores de ingresos, tendremos el mismo número de ingresos relativos promedio, uno para cada receptor. En este punto, optaremos por la media geométrica de estos ingresos para calcular el ingreso relativo promedio de la sociedad. Esto es, 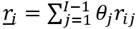 . Luego, considerando la ecuación (5), la ecuación del ingreso promedio del receptor, quedará como:
. Luego, considerando la ecuación (5), la ecuación del ingreso promedio del receptor, quedará como:
Ahora, en la medida que el número de receptores I sea lo suficientemente grande, podríamos utilizar 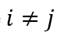 como una buena aproximación de
como una buena aproximación de 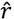 , donde
, donde
El índice de desigualdad de ingreso relativo
1. Como expresión normativa
Para la construcción del nuestro índice de desigualdad de ingreso relativo consideraremos como dada una distribución de ingresos cualesquiera 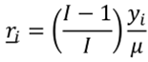 tal que
tal que 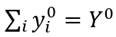 . Por otro lado, como ocurre con los índices de desigualdad de Dalton (1920) y Atkinson (1970), la diferencia entre el bienestar de máximo bienestar social y el bienestar efectivo se continúa considerando como una medida de la desigualdad de ingresos. Así, el índice de desigualdad de ingresos que proponemos y al que denotaremos como IDIR (índice de desigualdad de ingreso relativo) conceptualmente, vendría dado por,
. Por otro lado, como ocurre con los índices de desigualdad de Dalton (1920) y Atkinson (1970), la diferencia entre el bienestar de máximo bienestar social y el bienestar efectivo se continúa considerando como una medida de la desigualdad de ingresos. Así, el índice de desigualdad de ingresos que proponemos y al que denotaremos como IDIR (índice de desigualdad de ingreso relativo) conceptualmente, vendría dado por,
Entonces, bajo el marco normativo propuesto según el criterio de bienestar de Nash, las ecuaciones (2) y (4); nos permitirán especificar el IDIR como una relación entre el ingreso medio geométrico y el ingreso medio aritmético. Esto es,
Este resultado, coincide con la especificación del índice de Atkinson para cuando el coeficiente de aversión a la desigualdad es igual a 1 (Medina, 2001).
2. Como expresión positiva
En esta perspectiva, considerando la aproximación del ingreso relativo promedio agregado que ha sido señalada en la ecuación (7), y tomando el IDIR según la ecuación (9), podemos derivar el índice como una expresión de una medida objetiva. Esto es,
Así, un cambio en la distribución de ingresos, dado Y, que implique un incremento del ingreso relativo agregado, equivale a un aumento del ingreso promedio geométrico. Esto es, un incremento del bienestar social efectivo. A su vez, esto significaría que v se aproxima a 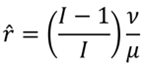 , ya que la relación media aritmética y media geométrica, para toda distribución, verifica (Karelin, Rondero, & Tarasenko, 2008):
, ya que la relación media aritmética y media geométrica, para toda distribución, verifica (Karelin, Rondero, & Tarasenko, 2008):
Nótese, según (11), la equiparación de ambas medidas ocurrirá sólo si se da la igualdad de ingresos entre los receptores, esto es  . El bienestar social efectivo es socialmente óptimo. En este caso único, se obtiene un IDIR = 0. Luego, para cualquier otro caso, se obtiene
. El bienestar social efectivo es socialmente óptimo. En este caso único, se obtiene un IDIR = 0. Luego, para cualquier otro caso, se obtiene 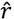 . Además, si algún receptor no percibe ingreso
. Además, si algún receptor no percibe ingreso 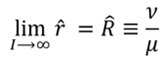 , entonces por definición se tiene IDIR = 1. Esto es, dado el marco informacional de la función de bienestar social, para dicha distribución existe un perceptor que no ha salido del statu - quo. No interesa como se distribuye el ingreso entre el resto de individuos.9 El mismo resultado se obtendrá si el ingreso total
, entonces por definición se tiene IDIR = 1. Esto es, dado el marco informacional de la función de bienestar social, para dicha distribución existe un perceptor que no ha salido del statu - quo. No interesa como se distribuye el ingreso entre el resto de individuos.9 El mismo resultado se obtendrá si el ingreso total 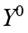 le corresponde sólo a un único receptor mientras que el resto de receptores posee cero ingresos.
le corresponde sólo a un único receptor mientras que el resto de receptores posee cero ingresos.
En consecuencia, si existe igualdad en la distribución de ingresos entre los receptores el índice será IDIR = 0 y si se tiene que el ingreso total le corresponde a un solo receptor entonces el índice será IDIR = 1. Luego, el índice de desigualdad estará acotado entre 0 y 1, esto es 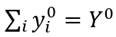 .
.
Por razones pedagógicas se muestra una representación gráfica. Para tal caso supondremos una sociedad donde I = 2 y la distribución de ingresos viene dada por el vector 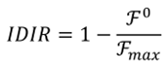 , donde
, donde 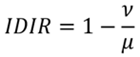 y
y 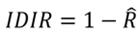 . La figura (1) muestra la relación media aritmética - media geométrica y su relación con la función de bienestar de Nash, siendo la función de bienestar de Nash generalizado igual a
. La figura (1) muestra la relación media aritmética - media geométrica y su relación con la función de bienestar de Nash, siendo la función de bienestar de Nash generalizado igual a 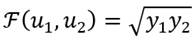 .
.
3. Propiedades
Siguiendo a Villar (2017), podemos verificar cuáles son las propiedades que el IDIR cumple. De acuerdo a las demostraciones desarrolladas en el anexo A, podemos afirmar que el índice de Desigualdad del Ingreso Relativo verifica las propiedades de normalización, de simetría, del principio de transferencia de Dalton, de continuidad y de independencia de escala. Por otro lado, el mismo índice incumple las propiedades del principio de réplica de poblaciones y la de descomponibilidad.10
Cálculos del índice bajo distribuciones simuladas
Considerando que en los países subdesarrollados con mayor recurrencia las distribuciones de ingresos efectivas se describen mediante distribuciones con una mayor asimetría (Figueroa, 1993), realizaremos simulaciones tomando como aproximaciones de las distribuciones de ingreso, las distribuciones estadísticas de Pareto, la log normal y la log logística. Las simulaciones se realizarán sobre una muestra aleatoria de tamaño n = 1000000 observaciones, escogidos para un rango de ingresos establecido arbitrariamente y utilizando las librerías del programa R para cada distribución.
Además, estas distribuciones teóricas presentan buenas propiedades estadísticas, asimismo algunas de ellas presentan un buen ajuste a las distribuciones empíricas. En este sentido, es recurrente el uso de estas distribuciones en la literatura sobre la distribución, no sólo para simulaciones sino además, para realizar ajustes estadísticos (Campano & Salvatore, 2006; Cowell, 2013; Gasparini, Cicowiez & Sosa, 2013).
Asimismo, calcularemos para efectos de una comparación posterior, el índice de desigualdad de Gini para cada una de las distribuciones simuladas.11 La comparación de los resultados simulados del GINI y del IDIR nos permitirá ver que tan bien se comporta este último al medir la desigualdad.
Distribución de Pareto
Dada la función de densidad de probabilidad de Pareto (Dagum, 1980; Cowell, 2011):
Donde  ,
, 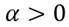 y
y 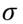 como un parámetro de escala, directamente proporcional a la varianza de la distribución.
como un parámetro de escala, directamente proporcional a la varianza de la distribución.
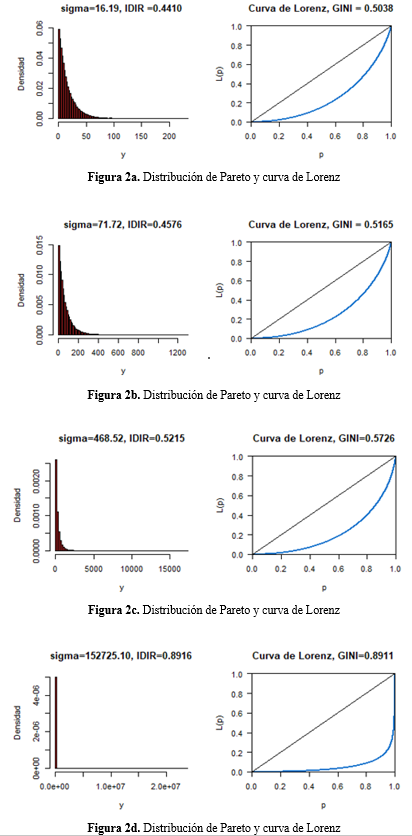
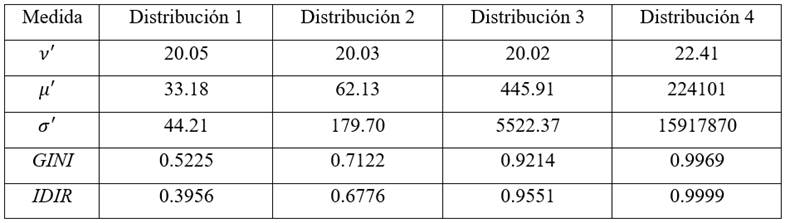
Para una simulación de n = 1000000 receptores,12 supondremos cuatro distribuciones de ingresos entre los receptores, las que se construirán arbitrariamente. Así, por ejemplo, para la primera distribución se considerará un intervalo de ingresos entre 0 y 1200, tal como se observa en la figura 2a; de tal manera que podamos tener la certeza de que la variabilidad de los parámetros de la distribución cuenta con una adecuada representatividad, donde las cuatro distribuciones se han simulado con una escala igual a scale = 1000. Utilizando el software R obtenemos para cada una de las distribuciones, que corresponden a cada uno los diferentes valores de los parámetros tomados como argumentos, los siguientes resultados:13
Para la simulación de distribución 1 tenemos una media geométrica igual a ν = 8.88, una media aritmética igual a 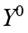 15.89 y una desviación estándar igual a
15.89 y una desviación estándar igual a 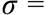 16.19. Luego, de acuerdo a lo formulado en las ecuaciones 9 y 10 obtenemos el IDIR igual a 0.4410. En tanto que el GINI calculado es igual a 0.5038 aplicando el procedimiento señalado en la nota de pie 11. Para el resto de las distribuciones simuladas, se tienen las mismas interpretaciones. Es importante notar que, de acuerdo a la desviación estándar, se tratan se distribuciones simuladas con una dispersión cada vez mayor. Así, la distribución 4 es la que posee una mayor dispersión con un
16.19. Luego, de acuerdo a lo formulado en las ecuaciones 9 y 10 obtenemos el IDIR igual a 0.4410. En tanto que el GINI calculado es igual a 0.5038 aplicando el procedimiento señalado en la nota de pie 11. Para el resto de las distribuciones simuladas, se tienen las mismas interpretaciones. Es importante notar que, de acuerdo a la desviación estándar, se tratan se distribuciones simuladas con una dispersión cada vez mayor. Así, la distribución 4 es la que posee una mayor dispersión con un 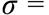 152 275.10. Esta mayor dispersión de las distribuciones se hará evidente al calcular un mayor IDIR y un mayor GINI respectivamente.
152 275.10. Esta mayor dispersión de las distribuciones se hará evidente al calcular un mayor IDIR y un mayor GINI respectivamente.
En las figuras 2.a - 2.d se representan las distribuciones y las curvas de Lorenz para cada una de las cuatro simulaciones bajo una distribución de ingreso de Pareto.
De acuerdo a los resultados obtenidos bajo la distribución de Pareto, la cual es asimétrica, se observa que en la medida que la dispersión de los ingresos y el índice GINI sean mayores, el IDIR también aumenta. Por cada punto porcentual que aumenta la desigualdad, entre una y otra distribución, según el índice de GINI, el IDIR responde con incrementos relativamente positivos y se hace menos sensible para distribuciones altamente desiguales:
Tabla 2 Sensibilidad del IDIR ante un aumento de GINI en un punto porcentual
| De la distribución 1 a 2 | De la distribución 2 a 3 | De la distribución 3 a 4 |
| 1.4932 | 1.2856 | 1.2759 |
En la primera simulación, como desarrollamos en la parte teórica, un IDIR calculado igual a 0.4411 supone una diferencia entre el bienestar máximo y el bienestar efectivo de 10 a 6; en tanto que un IDIR igual a 0.8916, tal como se obtiene en la distribución 4, supone una brecha mayor entre el bienestar máximo y el bienestar efectivo, de 10 a 2. Así, en la medida que el IDIR sea mayor, el bienestar social es menor.
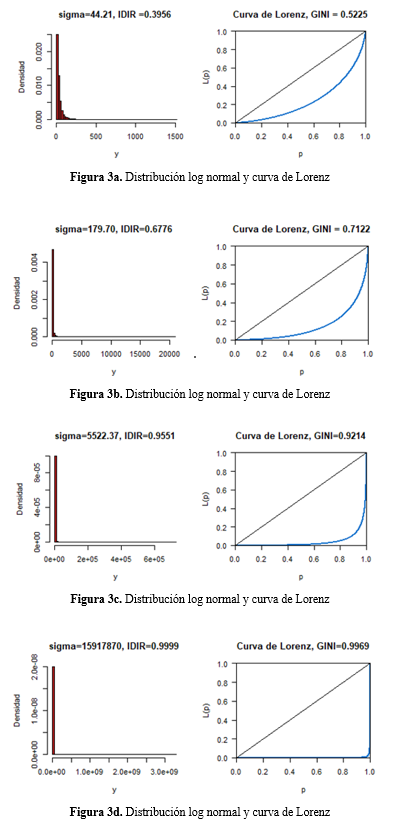
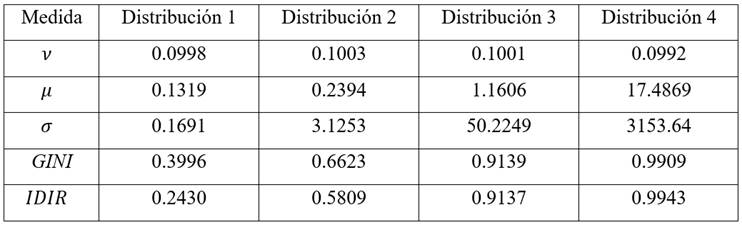
Distribución log normal
Ahora consideraremos una distribución log normal (Evans & Rosenthal, 2004),
donde 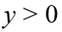 ; siendo, para esta distribución,
; siendo, para esta distribución, 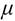 y
y 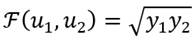 la media aritmética y la desviación estándar del logaritmo de la variable.
la media aritmética y la desviación estándar del logaritmo de la variable.
Para una simulación de n = 1000000 receptores, supondremos cuatro distribuciones de ingresos entre receptores, las cuatro distribuciones con un log ingreso medio 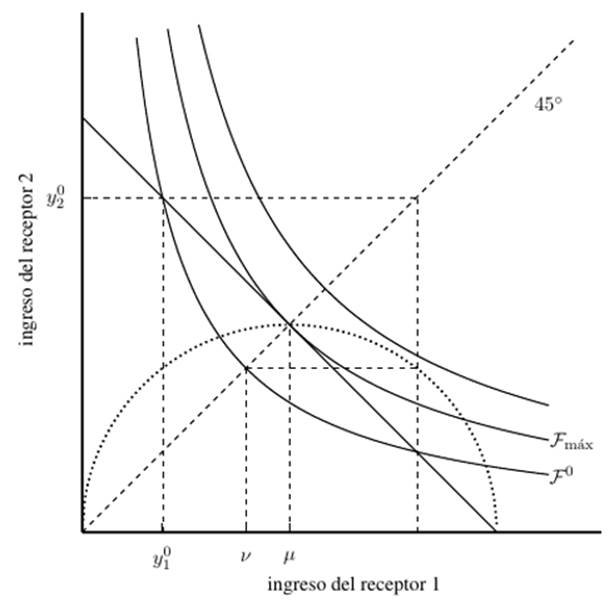 3 aproximadamente, pero con diferentes desviaciones estándar. Utilizando el software R obtenemos los siguientes resultados:14
3 aproximadamente, pero con diferentes desviaciones estándar. Utilizando el software R obtenemos los siguientes resultados:14
donde 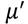 y
y 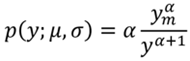 son las notaciones correspondientes a la media aritmética y la media geométrica de la distribución de ingresos. A continuación, representamos las distribuciones log normal y sus respectivas curvas de Lorenz en las figuras 3a - 3d.
son las notaciones correspondientes a la media aritmética y la media geométrica de la distribución de ingresos. A continuación, representamos las distribuciones log normal y sus respectivas curvas de Lorenz en las figuras 3a - 3d.
Observamos, que la mayor dispersión de cada distribución recogida por la desviación estándar 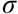 presentada en el Tabla 3, en las figuras 3a, 3b, 3c y 3d se recoge con una curva de Lorenz con una mayor distancia vertical respecto a la línea de igualdad respectivamente. Es decir, la distribución 4 presenta una mayor desigualdad que la distribución 3, esta respecto a la distribución 2 y esta mayor que la primera. Vamos de una simulación de distribución de mayor a menor dispersión y en consecuencia, de acuerdo a la curva de Lorenz, de menor a mayor desigualdad. Nótese además, que en las distribuciones log normal que hemos simulado manteniendo contante el log medio, no suponemos un ingreso aritmético constante de los ingreso, ya que en la medida que aumentamos la dispersión en la distribución log normal, implicará ingresos máximos e ingresos mínimos con mayores amplitudes. Así, para las cuatro distribuciones simuladas con dispersiones
presentada en el Tabla 3, en las figuras 3a, 3b, 3c y 3d se recoge con una curva de Lorenz con una mayor distancia vertical respecto a la línea de igualdad respectivamente. Es decir, la distribución 4 presenta una mayor desigualdad que la distribución 3, esta respecto a la distribución 2 y esta mayor que la primera. Vamos de una simulación de distribución de mayor a menor dispersión y en consecuencia, de acuerdo a la curva de Lorenz, de menor a mayor desigualdad. Nótese además, que en las distribuciones log normal que hemos simulado manteniendo contante el log medio, no suponemos un ingreso aritmético constante de los ingreso, ya que en la medida que aumentamos la dispersión en la distribución log normal, implicará ingresos máximos e ingresos mínimos con mayores amplitudes. Así, para las cuatro distribuciones simuladas con dispersiones 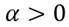 , donde
, donde 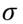 corresponde a las dispersiones de las cuatro distribuciones normales simuladas, se tiene como resultado un IDIR cada vez mayor
corresponde a las dispersiones de las cuatro distribuciones normales simuladas, se tiene como resultado un IDIR cada vez mayor
Es decir, la mayor amplitud y dispersión que recoge la distribución log normal es penalizada por el IDIR en mayor medida aunque con menor sensibilidad cada vez. Así, por cada punto porcentual que aumenta la desigualdad de la distribución, entre una y otra, según el índice de desigualdad de GINI, el IDIR también aumenta pero con incrementos relativamente cada vez menores, tal como se muestra en la siguiente tabla:
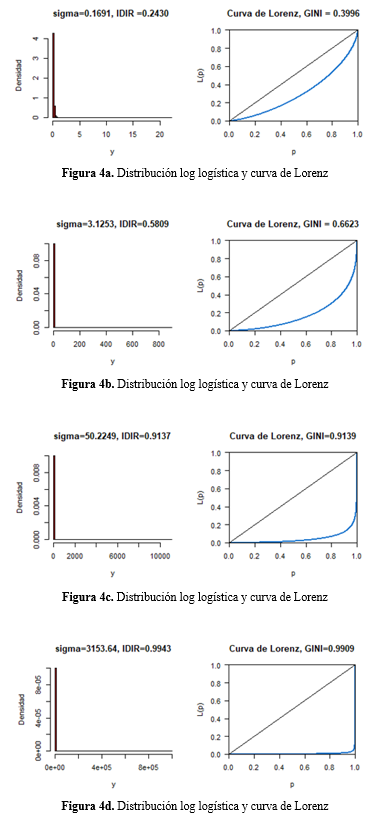
Distribución log logística
Finalmente, simularemos que la distribución de ingresos sigue una distribución log logística (Campano & Salvatore, 2006),
donde 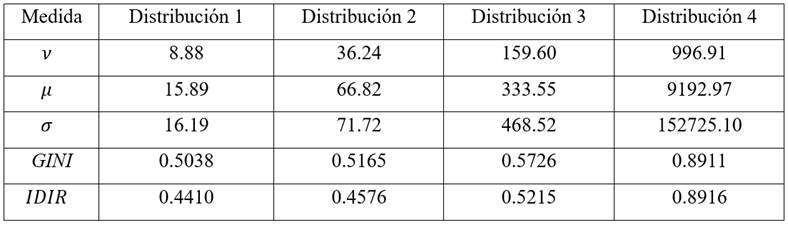 es el parámetro de escala y m es el logaritmo del ingreso mediano.
es el parámetro de escala y m es el logaritmo del ingreso mediano.
Siguiendo el algoritmo, para una simulación de n = 1000000 receptores, supondremos cuatro distribuciones de ingresos entre los receptores, donde las cuatro distribuciones se han simulado con una escala igual a scale = 10. Utilizando el software R obtenemos los siguientes resultados:15
Presentamos las distribuciones log logísticas simuladas y sus respectivas curvas de Lorenz en las figuras 4a - 4d.
En la tabla anterior, se observa, al igual que en las anteriores simulaciones, que en la medida que aumenta la dispersión de la distribución, el IDIR también aumenta. Asimismo, para la distribución log logística, la sensibilidad de la respuesta del IDIR es positiva pero cada vez menor por cada punto porcentual que aumenta la desigualdad de la distribución, entre una y otra, según el índice de GINI. Entonces, el IDIR responde con incrementos relativamente cada vez menores:
La relación IDIR y el GINI
Siguiendo a (Kendall & Stuart, 1977) se obtiene una medida de la dispersión llamada diferencia media. A partir de este concepto se puede plantear una forma de medir el índice de Gini basado en la diferencia media. Luego, dadas ciertas propiedades de esta forma de medición será posible plantear el índice de Gini de la siguiente manera (Villar, 2017):16
Luego, dado el índice de desigualdad IDIR formulado en la ecuación (9), podemos derivar, con objeto de presentar evidencia posteriormente, una relación lineal positiva entre los índices IDIR y GINI,
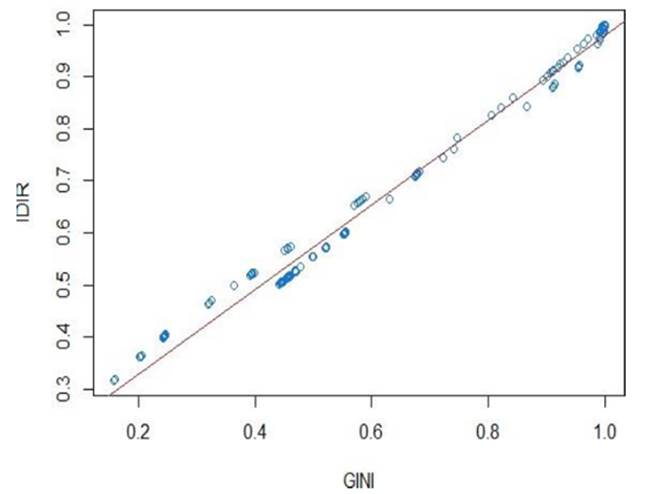
Ahora, retomando las distribuciones de Pareto, la log normal y la log logística; y realizando un número mayor de simulaciones para cada una de las distribuciones, encontramos entre el IDIR y el GINI una coeficiente de correlación equivalente a 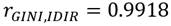 .
.
El cálculo del IDIR para el Perú, 2004-2017.
De los datos utilizados
Para efectos de la aplicación del índice propuesto se midió la desigualdad para cada uno de los veinticuatro departamentos del Perú, para el periodo comprendido entre los años 2004 y 2017. La medición se realizó tomando como una unidad receptora a los hogares, y se toma como medida el ingresos que se calcula a partir de la información obtenida de las “Encuestas Nacionales de Hogares ENAHO” del 2004 al 2017 implementadas por el Instituto Nacional de Estadística e Informática del Perú.
En nuestro cálculo tomaremos como objeto de medición el ingreso del hogar, denotado como ingtot según la codificación de la ENAHO. Este ingreso posee la siguiente composición:
1. Ingreso de trabajo (ingtrab):
1.1. Ingreso de trabajo salarial (ingtrabw):
ingtrabw = ingnethd + pagesphd + insedlhd + paesechd
donde:
ingnethd: ingreso monetario neto de la actividad principal dependiente.
pagesphd: ingreso por pago en especie de la actividad principal dependiente.
insedlhd: ingreso neto de la actividad secundaria dependiente.
paesechd: ingreso pago en especie de la actividad secundaria dependiente.
1.2. Ingreso de trabajo no salarial (ingtrabs):
ingtrabs = ingindhd + ingauthd + ingseihd + isecauhd
donde:
ingindhd: ingreso por actividad principal independiente.
ingauthd: ingreso por autoconsumo de la actividad principal independiente.
ingseihd: ingreso neto de la actividad secundaria independiente.
isecauhd: ingreso por autoconsumo de la actividad secundaria independiente.
ingtrab = ingtrabw + ingtrabs
2. Ingreso de propiedad (ingprop):
ingprop = ingrenhd + ia01hd
donde:
ingrenhd: ingreso monetario por rentas de la propiedad.
ia01hd: ingreso alquiler imputado de la vivienda.
3. Ingreso de transferencias privadas (trapriv):
trapriv = ingtrahd + ingtexhd + ia02hd
donde:
ingtrahd: ingreso por transferencias corrientes monetarias del país.
ingtexhd: ingreso por transferencias corrientes del extranjero.
ia02hd: ingreso por transferencia de alquiler.
4. Ingreso extraordinario (ingextr):
ingextr = ingexthd + ingoexhd
donde:
ingexthd: ingresos extraordinarios por trabajo.
ingoexhd: otros ingresos extraordinarios.
Finalmente, obtenemos nuestro ingreso total del hogar:
ingtot = ingtrab + ingprop + trapriv + ingextr
Los resultados del cálculo del IDIR departamental
Al utilizar la variable “ingreso ingtot” para calcular el IDIR de cada departamento del Perú, para el periodo 2004 - 2017, se han obtenido resultados cuyo resumen estadístico se presenta en el Tabla 7. De acuerdo al resumen, los departamentos que presentan una menor desigualdad, en promedio, son Ica (0.22), Tumbes (0.24), Lambayeque (0.27) y Madre de Dios (0.27). En tanto que, Ayacucho (0.41), Huánuco (0.40), Puno (0.40) y Cajamarca (0.41) presentan un índice mayor. Del primer grupo de departamentos, los tres primeros se ubican en la costa del Perú y su actividad económica presenta una importante participación de la agroindustria; en tanto que del segundo, todos se ubican en la sierra, donde es preponderante la actividad minera.
Tabla 7 Medidas estadísticas del IDIR por departamento
| DPTO | mean | sd | median | min | max | range | skew | kurtosis |
| AMA | 0.36 | 0.02 | 0.36 | 0.32 | 0.41 | 0.09 | 0.51 | 0.51 |
| ANC | 0.36 | 0.03 | 0.36 | 0.30 | 0.42 | 0.12 | -0.28 | -0.88 |
| APU | 0.39 | 0.07 | 0.38 | 0.31 | 0.52 | 0.21 | 0.53 | -0.95 |
| ARE | 0.31 | 0.04 | 0.31 | 0.24 | 0.38 | 0.14 | -0.02 | -0.65 |
| AYA | 0.40 | 0.03 | 0.40 | 0.37 | 0.46 | 0.09 | 0.55 | -0.97 |
| CAJ | 0.41 | 0.03 | 0.41 | 0.36 | 0.45 | 0.09 | -0.11 | -1.50 |
| CUS | 0.38 | 0.03 | 0.38 | 0.35 | 0.42 | 0.07 | 0.00 | -1.52 |
| HCV | 0.39 | 0.05 | 0.40 | 0.32 | 0.46 | 0.14 | -0.25 | -1.26 |
| HUA | 0.40 | 0.04 | 0.39 | 0.36 | 0.48 | 0.13 | 0.80 | -0.37 |
| ICA | 0.22 | 0.04 | 0.21 | 0.16 | 0.29 | 0.13 | 0.25 | -1.48 |
| JUN | 0.32 | 0.03 | 0.32 | 0.27 | 0.36 | 0.10 | -0.05 | -1.02 |
| LAM | 0.27 | 0.02 | 0.26 | 0.24 | 0.31 | 0.07 | 0.44 | -1.48 |
| LIM | 0.29 | 0.03 | 0.30 | 0.26 | 0.34 | 0.08 | 0.07 | -1.30 |
| LLI | 0.37 | 0.04 | 0.36 | 0.33 | 0.47 | 0.14 | 1.76 | 2.78 |
| LOR | 0.38 | 0.02 | 0.38 | 0.34 | 0.42 | 0.07 | 0.23 | -0.99 |
| MDI | 0.27 | 0.03 | 0.26 | 0.23 | 0.31 | 0.08 | 0.00 | -1.58 |
| MOQ | 0.40 | 0.02 | 0.40 | 0.37 | 0.46 | 0.07 | 0.59 | -0.46 |
| PAS | 0.35 | 0.03 | 0.35 | 0.31 | 0.42 | 0.11 | 0.75 | -0.28 |
| PIU | 0.32 | 0.02 | 0.32 | 0.28 | 0.35 | 0.07 | -0.41 | -1.04 |
| PUN | 0.40 | 0.03 | 0.39 | 0.37 | 0.46 | 0.10 | 0.73 | -0.36 |
| SMA | 0.37 | 0.04 | 0.37 | 0.32 | 0.43 | 0.12 | -0.03 | -1.21 |
| TAC | 0.30 | 0.02 | 0.30 | 0.26 | 0.34 | 0.08 | 0.02 | -1.29 |
| TUM | 0.24 | 0.02 | 0.25 | 0.21 | 0.27 | 0.05 | -0.46 | -0.92 |
| UCA | 0.28 | 0.06 | 0.27 | 0.20 | 0.38 | 0.18 | 0.29 | -1.55 |
Por otro lado, durante el periodo de estudio no todos los departamentos evidencian el mismo patrón de comportamiento de la desigualdad según el IDIR. Por ejemplo, Apurímac evidencia una mayor variabilidad, posee una desviación estándar de 0.7 y tiene una caja de bigotes con un mayor recorrido intercuartílico. En tanto que, el departamento de Amazonas es uno de los que presenta una menor variabilidad, 0.2, y un rango de 0.09.17
Para un mayor detalle de los resultados del cálculo obtenido para cada departamento y para cada año entre el 2004 y el 2017, véase el anexo B.
La estimación de la relación entre el IDIR y el GINI
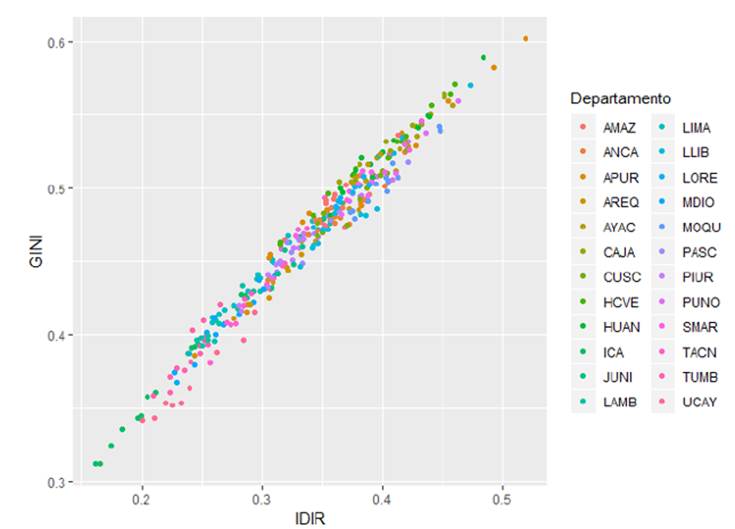
El índice de ingreso relativo, para efectos de la aplicación, muestra una relación estrecha con el índice de Gini tal cual se obtuvo en las simulaciones para el caso de la distribución del ingreso ingtot. Es decir, tan igual como el GINI, el IDIR mide la desigualdad.18 Así, el coeficiente de correlación estimado para Perú es, 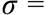
Sin embargo, a diferencia del GINI, el IDIR penaliza más la desigualdad, asignándole un número menor a distribuciones más desiguales. En términos de mejora de la distribución, la sociedad deberá mejorar mucho más para escalar en el índice IDIR. Véase la relación estimada en la figura 6.
De los resultados
De acuerdo a los cálculos efectuados para los departamentos del Perú, el índice de desigualdad de ingresos IDIR evidencia una heterogeneidad entre estos, lo cual es concordante con la literatura sobre la desigualdad en el Perú (Contreras et. al., 2015). Asimismo, siguiendo con la misma base de datos, el cálculo del índice propuesto muestra una relación positiva estrecha con el cálculo del índice de desigualdad de Gini departamental, llegando a obtenerse un coeficiente de correlación superior a 0.99. En este sentido, se tiene que, para distribuciones de ingresos con un índice de GINI mayor, le corresponde un índice IDIR mayor.
Así, los cálculos obtenidos para el Perú se comportan según los resultados que derivamos en las simulaciones efectuadas, evidenciándose empíricamente la relación lineal estrecha entre el IDIR y el índice de GINI tal cual se había obtenido en las simulaciones. Compárese las figuras 5 y 6.
Conclusiones
El trabajo propone una medida de la desigualdad de ingresos fundamentada en la economía del bienestar pero medible a través de estadísticos descriptivos. Asimismo, el índice propuesto recoge, a la luz de las simulaciones realizadas, la información que provee la mayor dispersión de ingresos asignándole a la distribución un mayor índice en la medida que sea mayor la desigualdad, según muestran las medidas simuladas del GINI en cada distribución. Por lo tanto, es un índice que penaliza con un mayor índice a las distribuciones más desiguales.
Por otro lado, el índice podría ser limitado para distribuciones donde no existen receptores con ingreso cero. Esto no sería una limitación desde una óptica de la justicia distributiva. Aun así, es posible extender la definición de receptor, por ejemplo trabajar con cuantiles, y sortear esta supuesta limitación. Se obtendría, en este caso valores positivos para el IDIR, aun sí las distribuciones contemplan receptores con un ingreso igual a cero. Y lo más importante, se efectúa distinguiendo las distribuciones más desiguales de las menos desiguales.
Un aporte de este índice no sólo es su simplicidad desde el punto de vista estadístico, sino que además, tiene la ventaja de estar fundamentado en un marco informacional de la teoría del bienestar social, específicamente en la función de bienestar social de Nash. Así, el ratio media geométrica - media aritmética, puede interpretarse como una lectura entre el bienestar social efectivo y el bienestar social máximo, lo cual es una ventaja sobre cualquier índice de desigualdad positivo, incluido el Gini, que carecen de una lectura explícita en términos de bienestar.
Asimismo, el IDIR complementa y fundamenta el caso particular del índice de Atkinson, cuando el índice de aversión a la desigualdad es igual a uno. Por lo tanto, da cuenta, más allá de una suposición, el por qué debiéramos utilizar, para estimaciones bajo el índice de Atkinson, un parámetro de aversión igual a uno, cuando se mida como una brecha entre el bienestar social efectivo y el bienestar social máximo. Se tendría así, un respaldo empírico que fundamente por qué debiéramos tomar 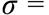 .
.
Finalmente, si bien el índice IDIR no cumple todas las propiedades deseables, entre ellas la descomponibilidad aditiva, sí cumple una propiedad muy importante: el principio de transferencia de Dalton, siendo útil para evaluar el impacto de las políticas redistributivas sobre la desigualdad.