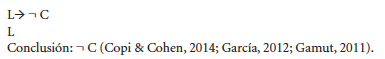Forma sugerida de citar:

Cárdenas-Marín, William Orlando, Reyes Solís, Darwin Bellini, & Viteri Bazante, Frank Bolívar (2017). La formalización lógica del lenguaje como punto de partida para el análisis objetivo del discurso y la argumentación científica. Sophia, colección de Filosofía de la Educación, 22(1), pp. 101-123.

Introducción

El presente artículo titulado La formalización lógica del lenguaje como punto de partida para el análisis objetivo del discurso y la argumentación científica , centra su atención en la evolución del análisis lógico del discurso, desde los planteamientos antiguos hasta las estructuras lógicas binarias que servirían de fundamento para la construcción de teorías científicas.

El objetivo del artículo es analizar los procesos de formalización del lenguaje a través de un análisis histórico de la lógica, para la determinación de los elementos lógicos que aportan a la formalización del lenguaje y a la construcción de argumentos científicos válidos.

El análisis lógico del lenguaje no constituye un estudio reciente y superfluo, sino que tiene larga tradición en el campo filosófico. A lo largo de la historia los análisis lógicos se han ido haciendo más profundos y estructurados, de manera que se ha consolidado como una ciencia válida para la estructuración del pensamiento, de manera que ha tenido un lugar fundante en la filosofía. Pero existen algunas escuelas del pensamiento que invalidan la funcionalidad de la formalización lógica del lenguaje, dado que argumentan en pro de una apertura lingüística, de manera que el lenguaje, para aquellos, no podría ser analizado lógicamente; estos postulados se observan principalmente en los planteamientos filosóficos que tienen una influencia pos-estructuralista, y desde estos aportes se hace de lado el componente lógico en el lenguaje. Este problema repercute en la comprensión que el individuo tiene de la filosofía, del lenguaje y de la construcción de la ciencia. De acuerdo con lo mencionado, en el ámbito académico se hace presente el problema de la exclusión del lenguaje lógico formalizado como elemento necesario para el análisis del discurso y la argumentación en la ciencia, dejando así al lenguaje desprovisto de los criterios de objetividad que la lógica aporta.

La importancia del tema radica en que, a raíz de lo mencionado en el párrafo anterior, ciertas vertientes de la filosofía con influencia pos-estructuralista defienden que el lenguaje tiene una amplitud que no puede ser abarcada por el análisis lógico, de manera que la lógica formal pierde todo valor para la realidad, pero sucede que los productos científicos, las teorías académicas y el lenguaje en general requieren de estructura y análisis lógico para su correcta comprensión; es aquí donde se hace evidente la actualidad de la temática planteada, dado que se considera de vital importancia reafirmar la necesidad y utilidad de la formalización lógica del lenguaje en la actualidad.

Para el desarrollo del artículo se han tomado en consideración las siguientes preguntas problematizadas: ¿Qué aportes filosóficos constituyen los postulados más relevantes para la evolución del análisis lógico? ¿Cuáles son las limitaciones que presenta la lógica clásica o aristotélica ante la lógica simbólica estructurada por Frege? ¿Cuáles son los aportes a partir de la formalización lógica del lenguaje para el análisis objetivo del discurso y la estructuración de argumentos científicos?

De acuerdo con lo que se ha mencionado, se sustenta la idea de que la formalización del lenguaje fortalece la objetividad de la argumentación científica y aquello permitiría que luego se puedan desarrollar aplicaciones tecnológicas.

La metodología utilizada en el documento es histórica-bibliográfica, analítica y crítica; esto porque se emplea recursos bibliográficos para recopilar datos históricos y procedimentales sobre la formalización lógica del lenguaje, se realiza una descomposición de los elementos fundamentales del análisis lógico con una explicación de dichos procesos de validación y, por último, se estructura un argumento crítico que valide la necesidad de categorías lógicas en el discurso y en la ciencia.

En un primer momento se realiza una ubicación general de los avances en las diferentes épocas para luego explicar el proceso de formalización lógico del lenguaje cotidiano a partir de la lógica clásica; luego de ello se postulan algunas limitaciones de la formalización clásica y se procede a explicar el proceso moderno de formalización; en un tercer momento, se hace referencia a la importancia del manejo formal del lenguaje en el análisis del discurso y la validación de teorías científicas, valorando el lenguaje formal de la lógica y de la matemática como sistemas para la construcción de la ciencia.

Elementos históricos sobre el análisis lógico formal del lenguaje

El problema del lenguaje constituye una de las principales preocupaciones de la filosofía a lo largo de la historia, aunque específicamente la preocupación no es por el lenguaje como tal, sino por las dimensiones en torno a su uso. Como ejemplo de este punto se puede tomar las alegorías de Zenón “donde se niega el principio de movimiento haciendo un uso inadecuado del principio de negación” ( ^{Sanguineti, 2000, p. 27} ), el cual es meramente lógico, aunque en aquella época no se le consideraba como tal, pues el problema en cuestión era el movimiento.

La sofistica, desde sus inquisiciones filosóficas, presenta una serie de argumentos y problemas en torno al lenguaje y al uso del mismo. Algunos de sus argumentos construidos para responder a Sócrates están cargados de una serie de detalles lógicos y filosóficos reducidos a juegos lingüísticos.

Luego de este periodo, Aristóteles presentó a la Lógica como Órganon. No se vuelca a hacer de este Órganon un asunto ontológico o un logos a ser analizado, sino que lo presenta como un instrumento que permite el conocimiento riguroso y válido: “La historia de la lógica comienza con Aristóteles, quien pudo decir con orgullo que había escrito el primer tratado de lógica formal” ( ^{Geach, 1985, p. 41} ).

La aristotélica se estructura como una lógica de relaciones entre sujeto-predicado dentro de la proposición o juicio y se da valor a la predicabilidad de los argumentos. De ahí que “Aristóteles parece haber dado con una diferencia que sirve para distinguir al menos aquellos nombres y predicables que dicen relación a objetos temporales” ( ^{Geach, 1985, p. 42} ). Luego el mismo autor presenta que lo predicativo del argumento se puede negar, mas no se puede negar el nombre que está en posición de sujeto ( ^{Geach, 1985} ). Aquí vemos que Aristóteles presenta preocupación particular por el lenguaje, aunque no se pueda llamar formalización como tal, sí se puede tomar como un primer paso hacia la reducción del lenguaje a partes sintácticamente simples para establecer una comprensión.

La construcción de silogismos y argumentos constituye un primer paso para formalizar el lenguaje: se busca formalizar con el fin de generar estructuras lingüísticas acordes a reglas que puedan ser fácilmente comprendidas. Formalizar el lenguaje no es una vanidad, sino que tiene un fin: facilitar la comprensión de lo que se quiere transmitir, dejar de lado ambigüedades que pueden generar problemas de comprensión: “En Aristóteles las ideas existen solo en la mente humana, pero se corresponden a la realidad, trae consigo el verdadero nacimiento de la lógica” ( ^{Sanguineti, 2000, p. 27} ).

Luego de Aristóteles aparece uno de los intentos más enigmáticos por estructurar una lógica formal, la que corresponde a la escuela Estoica-Megárica, que, basándose en reducciones, paradojas y el cálculo proposicional buscan generar una lógica formal en el lenguaje. Estos pensadores eran conocidos por su afición por la dialéctica y la retórica, pero el centro de la reflexión de esta escuela serán:

Los razonamientos proposicionales, que son clasificados como válidos o inválidos. Los primeros son definidos como aquellos en los que la negación de la conclusión es incompatible con la conjunción de las premisas. Estos pueden ser: verdaderos (premisas verdaderas) o falsos (cuando tienen por lo menos una premisa falsa o cuando no son válidos). Los argumentos verdaderos se dividen a su vez en demostrativos y no demostrativos. Los inválidos son aquellos en los que no se cumple la propiedad señalada para los válidos ( ^{Alessio, 2008, p. 38} ).

El valor de esta escuela es que permitió el desarrollo de una lógica sentencial axiomática en la que se plantea un análisis estructural de las conectivas, así como también de las propiedades formales de las mismas ( ^{Bochenski, 1976} ). Un aporte fundamental que permite comprender que la formalización del lenguaje en este recorrido histórico no se quedará estática en ninguna época, sino que se irá retroalimentándose, con nuevas propuestas.

También se le debe a este grupo de filósofos la paradoja del mentiroso ¹ , que ha generado una serie de problemáticas y discusiones a lo largo de la historia y que en la Edad Media será revisada exhaustivamente por parte de los estudiosos de la lógica.

“Durante la Edad Media, la lógica alcanzó un desarrollo notable, pues bebieron de varias fuentes: griegas, musulmanas, judías, y con sus propias aportaciones lograron una síntesis envidiable” ( ^{Campos Benítez, 2006, p. 208} ). Se retoman los problemas de la lógica que habían sido estudiados por los griegos, pero el tema principal radicará en la enseñanza de los problemas que se presentan en la lógica. Por ejemplo, el pensamiento en torno a la lógica y al lenguaje de Boecio a inicios de la Edad Media y, Guillermo de Ockham que cierra con el periodo medieval.

Boecio, comentarista y traductor de la obra Aristotélica, se convierte en puente entre la cultura grecolatina y la Edad Media, presentó también “una elaboración de la técnica en lógica formal… busca formular una regla de sustitución para las variables sentenciales; desde luego que no formula a manera de tal regla, sino mediante la descripción de la estructura de la formula” ( ^{Bochenski, 1976, p. 148} ). Puso estos temas como puntos de partida para el desarrollo de una larga discusión escolástica y medieval en torno al tema de las implicaciones ( ^{Bochenski, 1976} ). Boecio propondrá una serie de silogismos hipotéticos como conclusión de su especulación en torno al desarrollo de la lógica realizada por los estoicos, es un acercamiento a la formalización del lenguaje, busca una serie de reglas haciendo uso de conectores, reduciendo el lenguaje a sus estructuras básicas y presentando un análisis de la conclusión de las premisas desde la lógica aristotélica para proponer nuevas alternativas:

El reporte de Boecio sostiene que estas premisas negativas son equivalentes a afirmaciones de predicado indefinido (‘no capta’ = ‘es no captador’), por lo que se sugiere inmediatamente que Aristóteles aceptaría la equivalencia o la equipolencia entre proposiciones categóricas cuantificadas de distinta calidad (y los mismos términos), o sea que aceptaría la obversión o el Canon de Proclo y, en consecuencia, equivalencias formales en su lógica ( ^{Correia, 2013, p. 137} ).

De ahí que el comentario de Boecio constituya, con el aporte de otros pensadores, un análisis exhaustivo de la lógica aristotélica, aunque muchas veces se le señale como copista del pensamiento de Aristóteles: la empresa de traducir y comentar la obra del Estagirita es muy loable en las condiciones y contextos de aquella época, constituyéndose sus traducciones en libros oficiales de la época: “Esta versión latina fue la empleada como texto entre los libros académicos de la Logica vetus, hasta el siglo XIII. A la traducción hay que añadir las dos ediciones de sus comentarios” ( ^{García, 2012, p. 90} ).

La lógica en la Edad Media, resulta hasta la actualidad un ámbito desconocido y de cierto modo descuidado, sobre todo por lo temas centrales y transversales de la época. Aparecen autores que continúan con el legado griego, interpretándolo y comentándolo. Aquí aparecen Santo Tomas, Duns Escoto, Pedro Hispano, Guillermo de Shyreswood (Bochenski, 1976). No se tiene una visión panorámica de la lógica y la formalización del lenguaje en esta época, pero no se puede negar la existencia de intentos por entender a esta disciplina y al lenguaje desde la perspectiva que le se quiere dar en este trabajo. Aparecen problemas como las paradojas, los universales, la suposición, analogías, apelaciones, entre otros que se utilizan en los ámbitos escolásticos para el desarrollo de los temas filosóficos y teológicos imperantes en la época ( ^{Bochenski, 1976} ).

Otro autor fundamental en el desarrollo de la lógica es Guillermo de Ockham, quien en su obra Summa Lógica desarrolla la teoría del nominalismo extremo en la que se ubica el autor. Con el nominalismo responde sobre todo al problema de los universales, presentándolos como nombres que responden a conceptos que surgen de un proceso de cognición; es decir, responden a un paso de la experiencia sensible hasta la abstracción mental. En su obra presentará este problema de una manera magistral y claramente diferenciada: “La Suma de Lógica se compone de tres partes. En la primera de ellas, Ockham se ocupa de los términos, en la segunda, de las proposiciones y en la tercera, de los silogismos y formas de argumentación demostrativa” ( ^{Dueñas, 2013, p. 6} ). Por esto es fundamental comprender la importancia de la figura de Ockham en el desarrollo de la lógica pues este autor no solo intenta entender la lógica, sino que esboza una teoría en torno a ella:

En Ockham encontramos una innovación: considera también aquellos silogismos en los que una de las premisas se toma en sentido compuesto y otras en sentido dividido. Al mismo tiempo desarrolla formalmente con admirable penetración, toda la silogística modal partiendo de sus presupuestos estructurales ( ^{Bochenski, 1976, p. 239} ).

La proposición se postula como representación de la realidad, por lo que básicamente se preocupara por aquellos enunciados que tienen una relación directa con la realidad. Entonces se puede evidenciar que “el concepto universal es como una representación intelectiva y abstracta que se puede aplicar a muchos objetos en el mismo sentido” ( ^{Vanegas Carvajal, 2009, p. 173} ).

Guillermo de Ockham también se convierte en un revolucionario para su época, por el principio de economía, con el que busca separar aquellos conceptos innecesarios de los conceptos que permitan acercarse a la ciencia y a la realidad. De ahí que es fundamental comprender que la lógica de este autor busca encontrar las estructuras básicas del lenguaje para evitar decir cosas innecesarias. En su obra fundamental establecerá un análisis desde la proposición hasta la argumentación como tal, estableciendo desde allí este principio.

Una vez pasada la Edad Media, se abre paso una lógica de transición en la que nos encontraremos con Leibniz, quien rompe con la lógica venida de Port Royal, para introducir en la lógica aristotélica numerosos elementos nuevos o los que desarrolla de manera novedosa como son la elaboración de métodos de reducción, método de sustitución y el diagrama euleriano, es por esto que se lo llamará el padre de la lógica matemática ( ^{Bochenski, 1976} ).

Con el aparecimiento del problema de la ciencia moderna también van a aparecer otros ámbitos en los que la lógica va a encaminarse, sobre todo por la influencia de la matemática y la física en el desarrollo del lenguaje. Este nuevo lenguaje necesita recurrir a estas ciencias para constituirse en un lenguaje preciso que pueda responder a las necesidades de las nacientes ciencias:

“Este tipo de lógica consiste fundamentalmente en que las reglas de las operaciones se refieren a la forma de los signos y no a su sentido tal como en las matemáticas” ( ^{Bochenski, 1976, p. 282} ), es decir, se evidencia una preocupación esencial por la estructura del lenguaje dejando de lado lo que hay detrás. Otra de las revoluciones fundamentales de este nuevo tipo de lógica es “partir del sistema puramente formal para después pasar a una interpretación en el lenguaje ordinario” ( ^{Bochenski, 1976, p. 282} ) con el fin de establecer un lenguaje puro que esté lejos de los problemas de interpretaciones o de ambigüedades, es decir, caminar hacia un lenguaje que respete las reglas y así dar paso a la formalización.

Aparecen en este periodo autores como Frege, quien busca formalizar y axiomatizar el lenguaje de una manera precisa que luego será retomado por autores como Peano, Russell, Whitehead quienes se unirán al camino de desarrollar una lógica matemática y a simbolizar el lenguaje. Se llega a dos principios fundamentales: Toda verdad matemática puede ser traducida en verdad lógica y toda prueba matemática puede ser traducida en prueba lógica ( ^{Alessio, 2008, pp. 47-51} ).

El desarrollo de este tipo de lógica permitirá posteriormente pasar del lenguaje ordinario a la formulación de un lenguaje artificial que permitirá el desarrollo de algoritmos tecnológicos y aplicados a la ciencia, este paso permite así como en la Edad Moderna el despunte de la ciencia, a la lógica transformarse en una herramienta de la tecnología para formular programas, sistemas y demás aparatos que se constituyen en ejes de la vida actual.

El paso de la lógica clásica a la moderna lleva muchos siglos y por lo tanto se cometieron errores o se olvidaron ciertos aspectos, pero es fundamental comprender que este proceso de comprensión del lenguaje ha permitido la generación de los sistemas actuales. En el siguiente apartado se hace un recorrido explicativo desde la lógica clásica hasta la lógica simbólica contemporánea.

Nociones sobre la formalización clásica dellenguaje

Como se ha podido constatar en el apartado anterior el proceso de consolidación de la lógica desde sus inicios hasta los procesos contemporáneos ha tenido múltiples componentes, mismos que la han llevado a un nivel superior en el análisis del discurso y la validación de teorías científicas.

A continuación se explica el proceso de formalización lógico del lenguaje cotidiano en un primer momento a partir de la lógica clásica, y luego de ello se postularán las limitaciones de la formalización clásica y se procederá a explicar el proceso moderno de formalización.

El inicio de la lógica remonta, como ya se ha podido ver, a los estudios de Aristóteles sobre el lenguaje. En torno a las formas discursivas se esbozan leyes y reglas para el correcto razonamiento, mismas que siguen vigentes en la actualidad, a pesar de las nuevas indagaciones lógicas de la modernidad.

La lógica clásica se caracteriza por la descomposición de proposiciones y razonamientos, en términos simples que permitan validar su estructura. Al respecto ^{Gómez (2012)} enuncia que “La lógica clásica de predicados asume igualmente que la proposición atómica es la unidad del discurso asertórico. Por ende, allí cada enunciado complejo también es una cadena articulada de proposiciones atómicas” (p. 264).

El punto de partida para la formalización lógica es la realidad, entendida en la línea en la que Wittgenstein la explica, es decir como aquello que se da efectivamente, el darse efectivo de las cosas, lo concreto ( ^{Wittgenstein, 2001 [1921} ]). En sintonía con el autor, aquello que se puede enunciar, y los datos que interesan en el ámbito de la ciencia, son aquellos que parten de la realidad, los datos que pueden ser corroborados y replicados.

Si bien el punto de partida es lo concreto, el plano lógico no requerirá luego de lo concreto, sino que estructurará las leyes lógicas que rigen dicha realidad; a esto hace alusión ^{Cabanzo (2012)} cuando enuncia que “La lógica formal parte igualmente de lo concreto, el lenguaje cotidiano y sus argumentos, para ir haciéndose cada vez más abstracta. Nos suministra leyes y, posteriormente, estas leyes nos ayudarán en los casos particulares” (p. 19).

De acuerdo con lo que se ha mencionado, se hace evidente en el estudio lógico la existencia de reglas definidas sobre las que se deben estructurar los razonamientos empleados en el discurso. A continuación se esbozan los cuatro tipos de enunciados clásicos –aristotélicos– que se conocerán con el nombre de proposiciones categóricas ² , las mismas que poseen una calidad y cantidad, y tienen la condición de no repetirse ambas en una misma proposición, y reciben por nombre una vocal que defina su forma específica, de la siguiente manera:

Todo S es P – Universal, Afirmativa – Forma A

Ningún S es P – Universal, Negativa – Forma E

Algún S es P – Particular, Afirmativa – Forma I

Algún S no es P – Particular, Negativa – Forma O

Las cuatro proposiciones que se han enunciado constituyen los elementos necesarios para la construcción de un razonamiento, pero el lenguaje cotidiano demuestra que se hace bastante complicado hablar en términos proposicionales fijos, dado que si alguien menciona: las rosas son hermosas entonces dicho enunciado puede estructurarse en una proposición categórica del tipo A, de manera que se transforma a todas las rosas son hermosas . Si bien el ejemplo planteado es bastante sencillo, existen enunciados mucho más complejos, y convertirlos a su forma típica ³ implica un análisis más profundo, como el siguiente ejemplo muestra: si se dice que no todo lo que brilla es oro , entonces se busca la forma de encajar la oración en una proposición categórica que respete la cantidad y la calidad originales, situación que encaja en la proposición de tipo O algunas cosas que brillan no son oro ( ^{Copi & Cohen, 2014} ; ^{García, 2012} ; ^{Gamut, 2011} ).

Como se ha podido apreciar la labor de transformar el lenguaje cotidiano a una forma típica que permita validar su estructura se torna una labor compleja, pero necesaria, dado que solo así podrán analizare los razonamientos con el mayor rigor posible, eliminando ambigüedades en el discurso. En este sentido ^{Gómez (2012)} menciona que:

Una de las tareas básicas de la lógica consiste en investigar las condiciones bajo las cuales se puede asegurar que las verdad de un determinado enunciado A se desprende de otros enunciados… cuyas verdades ya se legitimaron… (p. 33).

Al hablar de cadenas de enunciados o cadenas proposicionales ya se entra al campo del razonamiento, el mismo que requiere un grado de análisis mayor, pero que se rige a reglas en las que no habrá cabida para excepciones discursivas.

Un razonamiento es una cadena de proposiciones categóricas y el nombre apropiado en el campo del análisis lógico es silogismo categórico. La lógica clásica clasifica los silogismos por su modo –el tipo de proposiciones categóricas que posee– y por su figura – la disposición que tienen sus términos dentro del silogismo. Así el razonamiento todo niño es goloso , puesto que los traviesos son golosos y los niños son traviesos pasaría a su forma típica así:

Todo travieso es goloso (proposición categórica de la forma A)

Todo niño es travieso (proposición categórica de la forma A)

Conclusión: Todo niño es goloso (proposición categórica de la forma A)

Además se puede ver que el término travieso que se repite en las dos proposiciones iniciales, llamadas premisas, y que se conoce como término medio, forma una figura designada como figura 1 –de las cuatro figuras posibles dada la distribución del término medio–. Así se estructura el razonamiento de forma silogística, situación que facilita decir si es válido o inválido lo que se dijo en lenguaje ordinario; en este caso es válido el razonamiento ya que, ya sea por validación por medio de Diagramas de Venn o a través de las reglas formales, todo silogismo de la forma típica AAA-1 es válido, sin importar el contenido existencial que posea ( ^{Copi & Cohen, 2014} ; ^{García, 2012} ; ^{Gamut, 2011} ).

Si bien la forma de análisis lógico clásico aún sigue vigente y sus reglas no entran en contradicción entre sí, estas formas tambalean cuando el individuo se enfrenta a estructuras proposicionales un poco más complejas, como en el caso de los condicionales. Tómese por ejemplo el condicional si hoy llueve, no iré a clase; está lloviendo , por ende no iré a clase ; ante este enunciado la lógica aristotélica o clásica pierde toda capacidad analítica, no habría forma de validar este tipo de argumentos con el análisis silogístico aristotélico. Es por ello que los lógicos modernos se vieron en la necesidad de revolucionar el análisis lógico, revolución que lleva a cabo Gottlob Frege ( ^{Martínez, 2010, p. 19} ).

Se analizará a continuación la importancia que presenta la lógica moderna al análisis del lenguaje, hasta el punto de ser necesaria la formalización para la estructuración de teorías válidas en el campo de la ciencia.

Formalización lógica contemporánea del lenguaje

Dadas las limitaciones que presentó la lógica clásica en el análisis y estructuración de lenguajes más complejos, y mucho más apegados al ámbito de las ciencias, se hace necesaria una lógica que mejore sustancialmente la simbolización y estudio del discurso, es así que según ^{Martínez (2010)}:

En el siglo XX la lógica da otro gran salto en dos sentidos respecto a la lógica antigua: a) formaliza de forma completa el lenguaje de las proposiciones con que se forman los razonamientos y b) se libera de la ontología antigua subyacente en el esquema ‘S es P’… (p. 19).

Este aporte se da principalmente en los estudios lógicos-matemáticos de Frege, quien inventa un sistema que pueda abarcar tanto las inferencias aristotélicas como aquellos argumentos en los que la lógica aristotélica no podía aplicarse. Frege desarrolla dicho sistema simbólico por su interés en las matemáticas, con la finalidad de demostrar que estas no eran más que una extensión de la lógica ( ^{Mounce, 1983, pp. 13-18} ).

La lógica contemporánea, que es conocida ampliamente como lógica simbólica, permite analizar argumentos mucho más amplios y los reduce a expresiones de corta extensión con la finalidad de facilitar su estructuración y, posteriormente, definir su validez y criterios de verdad. Tómese como elemento de análisis el ejemplo del apartado anterior:

Si hoy llueve, no iré a clase; está lloviendo, por ende no iré a clase

Este argumento puede fácilmente ser analizado y validado con las categorías lógicas fregeanas, de la siguiente manera:

Se designará con una letra a cada elemento atómico del argumento así, llueve = L, ir a clase = C, la negación de un término será representada por el símbolo ¬ que se usa tradicionalmente con dicho fin, por último se puede apreciar que el argumento es condicional, de manera que se empleará el conector funcional veritativo de la implicación →. Dada esta reducción de términos se obtiene el mismo argumento en su forma simbólica

El proceso presentado corresponde a la formalización del argumento, como se puede apreciar su estructura simbólica tiene menos palabras que el argumento en lenguaje cotidiano, es decir que se ha facilitado su comprensión de tal manera que incluso deja de lado las diferencias idiomáticas, es decir que así se tiene un esqueleto lógico que es común a todos los individuos del planeta que tengan cierto nivel de comprensión de lógica.

Pero la estructuración no es la finalidad de la formalización, sino que a raíz de ella se puede avanzar en el análisis lógico y se puede validar o invalidar el razonamiento, con la aplicación de diversos métodos, ya sea la aplicación de tablas de verdad o bien el proceso de deducción.

El argumento presentado es válido, dado que es parte de las reglas de deducción lógica y recibe el nombre de Modus Ponens , pero se puede corroborar su validez a través de tablas de verdad siguiendo la secuencia del razonamiento y colocando a los términos atómicos todos los ejemplos de sustitución posibles, así:

La validez del argumento es entonces corroborada por tablas de verdad, ya que en las filas donde las premisas L → ¬ C y L son ambas verdaderas, también la conclusión ¬ C es verdadera ( ^{Copi & Cohen, 2014} ; ^{García, 2012} ; ^{Gamut, 2011} ).

Como se ha demostrado hasta el momento el proceso moderno de simbolización, si bien parece hacer más complejo el análisis del lenguaje, más bien hace mucho más mecánica la validación de argumentos al simplificar los términos constitutivos de las proposiciones y determinar estructuras factibles de análisis. En ese sentido es relevante la aseveración de que “La lógica proposicional es el sistema lógico más simple y básico que existe. Sus constantes lógicas son las conectivas y la negación” ( ^{Gamut, 2011, p. 27} ).

A diferencia de lo que varios individuos plantean sobre el empleo de la formalización lógica y la poca relevancia que reporta para el análisis del lenguaje y la comprensión de las estructuras del conocimiento, se puede validar que su necesidad e importancia son indispensables, no se puede hacer ciencia sin bases lógicas, no se puede comunicar efectivamente sin estructuras lógicas, caso contrario el lenguaje se transformaría en una maraña de elementos ambiguos sin razón alguna, en esta línea es relevante lo que menciona Santamaría (2011) a continuación:

… los filósofos [y las personas que no emplean categorías lógicas en general] nos enredamos y confundimos fácilmente en discursos que en sus orígenes no representaban problema alguno; es como si estuviéramos hechizados a la hora de interpretar el lenguaje, enredando a nuestro paso toda la filosofía… más que dar respuestas definitivas, lo que la filosofía debe buscar y a lo que debe aspirar es a la claridad completa (p. 86).

Si bien la formalización lógica que se ha abordado en este apartado tiene una completa dirección deductiva, este tipo de inferencia es completamente válido para el análisis científico dado que al igual que la estructuración de las teorías científicas “El arte de la deducción o argumentación consiste en el dominio de las reglas lógicas que permiten extraer conclusiones partiendo de premisas” ( ^{García, 2012, p. 35} ), conclusiones que son válidas, como ya se ha tratado, siempre que la estructura sea lógicamente correcta.

De acuerdo con lo que se ha trabajado hasta el momento, la formalización permite analizar y validar lo que se dice, y dado que el hecho comunicativo es base de aquello que se estructura como ciencia, entonces el conocimiento de la lógica permite comprender de mejor manera el quehacer de las diversas ramas de la ciencia, es por ello que “… en conjunto, aunque desde diversas perspectivas epistemológicas, cada lógica adelanta una investigación sobre el razonamiento, sobre los mismos instrumentos del razonamiento y sobre las teorías que lo produce” ( ^{Gómez, 2012, p. 32} ), y después de avanzar en la comprensión del razonamiento, se hace posible la teorización coherente de nuevos postulados científicos.

En el siguiente apartado se aborda la importancia de la formalización del lenguaje a partir de diversos casos en los que se hace manifiesto este trabajo.

Aportes e importancia de la formalización lógica del lenguaje

Este acápite anhela mostrar la importancia de la formalización del lenguaje para la comprensión de la realidad y que dicha formalización no se opone a las funciones emotivas o directivas que posee el lenguaje, sino que es un campo diferente. La formalización de los lenguajes apoya la función informativa y argumentativa que posee el lenguaje, pero esto no le da un estatus de superioridad ni de inferioridad, sino que le ubican en un campo específico.

El lenguaje es un instrumento humano que permite comprender las diversas realidades que se presentan como tales, pero es un artificio que puede capturar la realidad, puede crear nuevos elementos de lo real o puede falsear el mundo que se presenta y engañar o generar aspectos falsos. Y ahí surge la complejidad de los análisis del lenguaje y las preocupaciones que la filosofía intenta dilucidar.

Frente a la posibilidad de los engaños del lenguaje y de sus usos, la lógica y en general el saber humano busca sistemas que permitan alcanzar un lenguaje que se convierta en un instrumento inequívoco, libre de falsas interpretaciones. Un lenguaje que permita un acercamiento a la realidad de los hechos y que elimine las posibilidades individuales de interpretación.

El lenguaje está lleno de emotividades, de sueños, fantasías y nada de ello es negativo, pues son funciones del lenguaje: expresar afectos, influir en el receptor y convencerle de algo, expresar emociones, generar mundos imaginarios literarios o artísticos son elementos cotidianos del lenguaje y son elementos vitales. Así se tiene que:

El lenguaje emotivo no tiene nada de anómalo, ni lo tiene el lenguaje no emotivo o neutro. Tampoco las almohadas o los martillos tienen nada de malo. Todo esto es cierto; pero no quiere decir que vayamos a tener éxito si tratamos de clavar clavos con almohadas, o que podamos sentirnos cómodos si tratamos de dormir apoyando nuestras cabezas sobre martillos ( ^{Ortiz, 1994, p. 28} ).

Ahora bien, entre esas funciones del lenguaje está la informativa ( ^{Copi & Cohen, 2014} ), aquella que refiere a un lenguaje usado para afirmar o negar proposiciones o para presentar razonamientos argumentativos. Y esa función lleva a otro campo del lenguaje, el que es motivo de estos apuntes.

Antes de enfrentar esta función se analizan ciertos prejuicios o imaginarios sociales que miran al lenguaje como algo mágico e inmediato y que genera errores permanentes o concepciones erradas de los usos lingüísticos:

a) La tentación de pensar que para iniciar una des-complejización de un acontecer se debe definir el término para así tenerlo claro y trabajar desde allí. Pero, esa dimensión solo revela ingenuidad, al pensar que definiendo el término se abarca la realidad, como si la definición fuese una ontología del ser. Esa es una noción medieval bastante superada en nuestros tiempos.

b) La concepción mágica de que al enunciar algo se convierte en una realidad, al enunciar la palabra, la realidad que esa palabra representa se convierte en un hecho concreto. Se escucha frecuentemente la idea mágica de que si repites lo que deseas se convierte en realidad, una idea que da a entender que solo enunciando la palabra, la realidad ontológica se hace.

c) La idea que los lenguajes emotivos son mejores que los lenguajes formales. Hoy corren por América Latina esnobismos teóricos defendiendo el sentir y atacando la razón y la ciencia, pidiendo que solo se sienta la realidad y que eso logrará un mejor ser humano. Sabiendo que son funciones diferentes del lenguaje y que sus usos especifican campos diversos de acción humana, se supera este prejuicio.

Ahora bien, la función informativa del lenguaje, aquella que refiere a un lenguaje usado para afirmar o negar proposiciones o para presentar razonamientos argumentativos. Es la búsqueda de un lenguaje emotivamente neutro, que reduzca o elimine la emotividad y que permita un texto en el que se pueda mantener la afirmación o negación de una proposición con base en datos empíricos o representaciones de acontecimientos que garanticen la proposición.

A partir de dichas proposiciones válidas se puede empezar a construir textos argumentativos que tiendan a defender o refutar un punto de vista frente a los interlocutores. En los lenguajes cotidianos la argumentación está presente en el diálogo, conversaciones o persuasiones en la que los interlocutores anhelan convencer al otro de la premisa planteada o de una conclusión a la que se ha llegado con base en una secuencia de proposiciones conectadas.

Como la función de la argumentación es convencer a otros acerca de la veracidad o aceptabilidad de lo que uno dice, las preguntas duraderas que la teoría de la argumentación estudia se relaciona con cuestiones de evaluación: qué es necesario para que una conclusión esté bien sustentada, qué criterios deberían regir la aceptación de un punto de vista, etc. Históricamente el estudio de la argumentación estuvo motivado por un interés en el mejoramiento del discurso o en la modificación de los efectos de ese discurso sobre la sociedad ( ^{Van Eemeren, Grootendorst, Jackson, & Jacobs, 2001, p. 308} ).

La teoría de la argumentación ha trabajado líneas que se independizan de la lógica formal y avanzan en racionalidades discursivas informales. Por ejemplo Tulmin en su texto Los usos de la argumentación (2003) trabaja desde una perspectiva discursiva sujeta a los contextos del mismo discurso que él denomina ‘campos de argumentación’ en donde se aleja del énfasis en las formas lógicas y pone la fuerza retórica en la situacionalidad de la argumentación, en el contexto del texto.

Sin desconocer el valor de este campo de la argumentación para cuestiones sociales como el derecho, la retórica política y los aportes generados para el avance del discurso social en las interlocuciones legales y políticas públicas, no es a este campo al que el trabajo quiere referir.

En el fondo, la argumentación quiere alcanzar conclusiones de mutuo acuerdo, aceptables para los actores del debate. No es tan fácil en los actos cotidianos, pues la argumentación generalmente se mezcla con creencias, deseos, intereses humanos que afectan a la estructura racional y coloca pasiones discursivas. Así una creencia puede ser defendida a tal punto que no importa el argumento, sino solo el hecho de querer conquistar la aceptación del otro. En este punto se tiene ya un campo de violencia discursiva. Y justo para evitar ese tipo de ejercicio discursivo es que la filosofía y en especial la lógica plantea alcanzar un lenguaje estándar formalizado. Y aquí ingresa un nuevo tema: la necesidad de formalizar el lenguaje y alcanzar una estructura lingüística universal. De esta manera se enuncia que:

Desde la lógica de Aristóteles, el estudio de la argumentación ha seguido la tradición del análisis de la forma de la inferencia argumentativa independientemente de su contenido. El desarrollo de la lógica simbólica moderna es una respuesta directa a la preocupación por representar formalmente la estructura inferencial de argumentos aparentemente aceptables o inaceptables ( ^{Van Eemeren, Grootendorst, Jackson, & Jacobs, 2001, p. 311} ).

Esa formalización del lenguaje ha permitido un campo positivo en el desarrollo del saber humano, sobre todo el saber científico y tecno científico, pues al desarrollar un lenguaje formal se logra un mundo de posibilidades cognitivas y/o tecnológicas. Formalizar el lenguaje permite ‘captar’ un acontecimiento o un conjunto de hechos que se repiten y, ponerlos en un modelo estándar que simplifique su comprensión, su funcionamiento, sus interrelaciones.

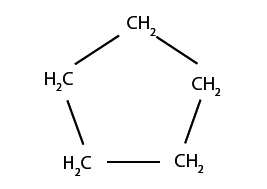
Ese modelo estándar es un artificio, un nuevo lenguaje que diga de aquello que se quiere mostrar. En química, por ejemplo, para traducir a un lenguaje formal fenómenos tan complejos como las combinaciones de elementos químicos naturales se realizan fórmulas que permiten captar esas realidades en un lenguaje simple, y libre de subjetividades. Por ejemplo: NaOH es la Soda cáustica, muy útil en la manufactura de papel, jabón y limpiadores; para una molécula orgánica es posible mostrar en un esquema que todos puedan entender su estructura, en una fórmula como la del ciclopentano cuyo uso aporta en el cuidado ambiental al momento de materiales de construcción (techos).

Figura 1

Así se logra un lenguaje formal en la ciencia, en la que se genera una nomenclatura básica y un sistema de relaciones que permiten traducir realidades simples o complejas. Un lenguaje científico que permite entendernos en un mismo idioma sobre los mismos fenómenos. Los ejemplos simples que se colocan en este trabajo, pero solo buscan poner en escena elementos generales de la formalización en diferentes áreas. En biología, por ejemplo, para explicar una realidad compleja como la del genoma humano se realiza una formalización en la que se puede mirar su conformación.

Figura 2

La formalización del lenguaje es un sistema simple que traduce una realidad a un esquema lingüístico científico. Eso universaliza en gran medida el saber y permite el acceso a las personas, muy contrario a la idea de que las estructuras formales limitan el conocimiento y reducen el saber solo a los especialistas. De hecho, un lenguaje formal como la matemática o la lógica son universales y por ello son de fácil acceso para gran parte de la población.

La lógica simbólica o matemática aportó elementos fundamentales para el desarrollo de la ciencia y de la tecnociencia al poner estructuras binarias de valor (verdadero/ falso 1/ 0) a las relaciones proposicionales. Por ejemplo, la conjunción, la disyunción, la implicación o la negación. Todas ellas con sus respectivos sistemas de valores en las diferentes posibilidades de verdad que se generan al relacionarse. Se muestra un simple ejemplo con la disyunción dada las proposiciones p q:

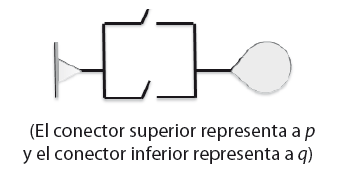
Las posibilidades son 4 y se puede representar en sistemas eléctricos o informáticos ( ^{Copi & Cohen, 2014} ; García, 2012; ^{Gamut, 2011} ). En el siguiente gráfico de un sistema disyuntivo (eléctrico) se puede ver su veracidad. Siendo p el primer interruptor y q el segundo interruptor, se combina las posibilidades de prender p o prender q para ver si el foco se prende o no. Si p está prendido y q está prendido, el foco sí se prende. Si p está prendido y q está apagado, sí se prende el foco. Si p está apagado y q está apagado no se prende el foco.

Figura 3

Se pueden colocar muchos ejemplos del uso tecno científico de los conectores; de hecho los aparatos electrónicos tienen estos elementos incorporados en sus estructuras de funcionamiento. Aunque el ejemplo es muy general, logra aproximar a la idea del funcionamiento de sistemas binarios: eso debido a tecnologías que aceptan solo dos valores, como la electricidad que permite prendido/apagado; pasa/no pasa, 1/0. Aunque hoy las nuevas lógicas y las nuevas tecnologías buscan y logran otros sistemas no binarios. La mecánica cuántica, la inteligencia artificial muestran estas nuevas realidades o nuevos retos lógico matemáticos. Así es importante mencionar que:

Si uno muestra que la ciencia requiere lógicas no bipolares, se está mostrando que ciertos capítulos de la ciencia no se comportan como lo exige la concepción tradicional; así por ejemplo: lo que podríamos llamar hoy la mecánica cuántica; la teoría que hoy se llama de la decisión; lo que suele llamarse la teoría de la preferencia, muy importante para analizar cualquier discurso de la teoría política, necesitan al menos tres valores de verdad; así, el principio de indeterminación de Heisenberg, para cuya comprensión dentro de la mecánica cuántica se muestra que se necesita suponer que la mecánica cuántica es un discurso científico con una lógica trivalente, donde los valores de verdad son: verdadero, falso e indeterminado (entonces el principio de tercero excluido hay que reemplazarlo por el principio de cuarto excluido) ( ^{Gómez, 1976, p. 41} ).

La lógica contemporánea presenta los límites de la formalización en sistemas binarios y la necesidad de ingresar en lógicas no bipolares, solo se enuncia este nuevo campo del saber lógico matemático de mundo de hoy. Se sabe además que las nuevas lógicas trabajan ya estos presupuestos y las tecnologías de punta aplican estas nuevas formalizaciones del lenguaje.

Conclusiones

Las teorías científicas o el desarrollo del pensamiento argumentativo han avanzado gracias a sistemas de formalización del lenguaje. Los saberes humanos cuyos lenguajes se formalizan evitan subjetividades y avanzan en la universalización de sus resultados permitiendo que se comuniquen de mejor manera y se distribuya los avances.

Los procesos históricos de la lógica han permitido profundizar en la comprensión del pensamiento humano, a la vez que han permitido su desarrollo y estructuración, para llegar a elementos contemporáneos superiores en relación con los postulados lógicos clásicos iniciales.

La lógica ha sido fundamental en el proceso de formalización del lenguaje para la producción científica y tecnológica de nuestra era. El aporte de los filósofos en el campo lógico desde los griegos, luego en el Medioevo, modernidad y etapa contemporánea han sido fundamentales para la construcción de teorías y explicaciones argumentativas en el proceso científico y tecnológico. Con esto se ve que la formalización del lenguaje ha sido procesual en la historia de la lógica y ha evolucionado en el tiempo.

Si bien la lógica clásica permitió analizar el razonamiento desde una perspectiva estructural, es la lógica simbólica postulada por Frege la que permite trabajar con elementos argumentativos y simbólicos que fueron empleados a plenitud en el desarrollo de sistemas computacionales y en la formulación de teorías científicas válidas.

Los sistemas lógicos tradicionales, como la lógica aristotélica, se ven limitados frente a las nuevas realidades y problemáticas que enfrentan las explicaciones y necesidades de las teorías científicas. Existen nuevos elementos y por tanto nuevas lógicas que recogen sistemas de comprensión diferente.

Las aplicaciones de las estructuras lógicas son diversas, y estos criterios son analizados en el desarrollo de nuevas tecnologías dado que, por ejemplo, la base de los sistemas computacionales se mueve en términos lógicos simbólicos y matemáticos.

Como recomendación para futuras investigaciones en la temática se postula que la lógica contemporánea presenta los límites de la formalización en sistemas binarios y la necesidad de ingresar en lógicas no bipolares, entonces podría investigarse el ámbito del desarrollo desde dichas lógicas que no han sido punto de enfoque en el presente artículo.