Introducción

La práctica docente de la matemática en el aula se ha visto fuertemente cuestionada por investigaciones, y la sociedad en general, en función de los resultados de procesos educativos. Actualmente se discute sobre la calidad de la práctica docente y de la educación, entendiendo a esta última como el grado de cercanía entre lo establecido en los fines del sistema educativo nacional y el logro de la población estudiantil (^{Gómez, 2007}).

En general, la práctica docente ha sido influenciada por reformas curriculares y corrientes teóricas que promueven nuevas formas sobre cómo desarrollar dicha experiencia. Según ^{Castro, Pino-Fan y Parra-Urrea (2018}), por más de tres décadas la comunidad de educadores de matemática ha estado interesada en describir, analizar y determinar el conocimiento requerido de esta ciencia para lograr procesos de enseñanza que garanticen el aprendizaje de sus estudiantes.

Por otra parte, la praxis pedagógica tradicional se caracteriza, según ^{Avendaño (2013}), por el trabajo mecánico y repetitivo al enseñar conocimientos específicos. En el caso de Ecuador esta praxis pedagógica está muy presente, así lo evidencian investigaciones como las de ^{Bravo, Trelles y Barrazueta (2017}) y ^{Suárez (2019}), además de la experiencia como docente del investigador en aulas de la Educación del Bachillerato General Unificado, independientemente de la formación que el educando haya tenido.

El empleo de una metodología tradicional formal del enfoque conductista por parte de los profesores es, en la gran mayoría de las veces, resultado de su propia experiencia como estudiante y, en el mejor de los casos, de su juicio sobre cómo las personas aprenden y se apropian de los conocimientos. La mayor parte de los docentes se caracterizan por tener habilidades y conocimientos para transmitir los contenidos que le son proporcionados a través de libros o documentos oficiales como los programas, pero sin poder ir más allá en la noción, sin conocer las razones de la existencia de tal o cual saber, tanto en la historia misma de la disciplina como en el currículo escolar.

De acuerdo a ^{Parra (2013}), ^{Garii y Silverman (2009}) y ^{Monaghan (2007}) la contextualización de las matemáticas por parte del profesor no es fácil y mucho menos automática, muy a pesar de que esta asignatura han sido producto de la cultura humana para satisfacer sus necesidades materiales y espirituales, los docentes tienen una capacidad limitada para contextualizar el conocimiento y deficiencias para vincular lo que imparten con otras disciplinas u otros niveles educativos, a pesar que “el pensamiento matemático se desarrolla en todos los seres humanos en el enfrentamiento cotidiano a sus múltiples tareas” (^{Cantoral, Farfán, Cordero, Alanís y Garza 2003}:19).

Luego, desde la experiencia del investigador principal, sólo algunos docentes cuentan con conocimientos didácticos para enseñar los contenidos eficazmente, pero no los ponen en práctica. Al mismo tiempo carecen de otros, como la utilidad y necesidad de la planeación, empleo y variación de estrategias pedagógicas activas para el proceso de enseñanza y aprendizaje o la utilización de recursos. Se caracterizan más que nada por el hecho de poseer las bases matemáticas indispensables para comprender y profundizar en los contenidos.

Esta situación se ha visto con mayor énfasis en Ecuador a partir de la última década, principalmente desde que otros profesionales ajenos al área de la docencia, tales como ingenieros, administradores, contadores u otros han ingresado a las instituciones educativas como profesores de matemática, sin tener una adecuada formación docente.

En este sentido, mientras que unos están más especializados en el saber, otros lo están, pero en un aspecto pedagógico, provocando que la intencionalidad de la enseñanza sea diferente. Por lo general, son pocos los profesores que tienen ambos conocimientos y saben integrarlos. Esto ha traído como consecuencia que los estudiantes no vinculen los temas estudiados en matemática con su cotidianidad, obteniendo así aprendizajes descontextualizados y sin sentido.

Por otro lado, los temas matemáticos, y en particular las funciones exponenciales, son de suma importancia para la comprensión de las actividades humanas, vinculadas a diversos campos tales como la economía, la biología, la física, la medicina o la demografía; sin embargo, son presentados sin vinculación alguna con estas áreas del conocimiento. En Ecuador encontramos inconvenientes en la forma de abordarlo por parte de algunos docentes; habitualmente es a través de la solución de ejercicios, elaboración de tablas de valores, realización de gráficas y estudio de la misma, este proceso requiere la inversión de mucho tiempo, dejando poco espacio para el análisis, las reflexiones y sus aplicaciones a las actividades humanas, trayendo como consecuencia un alto grado de dificultad por parte de los estudiantes para la comprensión de esta unidad curricular tan importante.

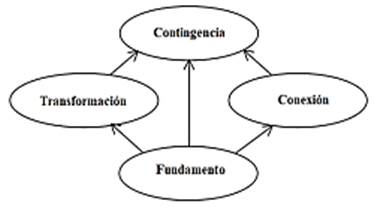
Con relación al conocimiento del contenido matemático por parte de los profesores, ^{Rowland et al. (2005}), realizaron un estudio sobre este conocimiento de profesores en formación de educación primaria del Reino Unido, para ello analizaron sesiones de clases de algunos educadores. Su objetivo fue localizar las formas en que se funda el conocimiento y la enseñanza del docente de matemática. El análisis de los datos obtenidos condujo a la identificación de un cuarteto de conocimiento, con cuatro categorías o unidades a través de los cuales se pueden observar los conocimientos matemáticos y didácticos puestos en práctica de los profesores. De esta forma se origina el modelo del cuarteto de Conocimiento (The Knowledge Quartet - KQ) cuyas categorías o unidades se denominan: fundamento, transformación, conexión y contingencia, tal como se muestran en la Figura 1.

Figura 1 Modelo el cuarteto de Conocimiento 

A continuación, se describen cada una de las categorías según ^{Rowland et al. (2005}):

Categoría 1. Fundamento. Se refiere al conocimiento, la comprensión per se y el saber necesario para enseñar matemáticas, así como las creencias sobre la naturaleza de esta ciencia. Las finalidades de la educación matemática y las condiciones sobre las cuales los alumnos aprenderán mejor también contempla el aprendizaje de los docentes, en la preparación intencionadamente o no, de su rol en el aula. Las componentes clave de este marco conceptual son: el conocimiento y la comprensión de las matemáticas, esta categoría coincide con lo que ^{Shulman (1987}) llama comprensión y lo relaciona con el conocimiento didáctico del contenido.

Categoría 2. Transformación. Este se basa en la observación propuesta por ^{Shulman (1987}) de los conocimientos para la enseñanza, caracterizados por la capacidad de un docente para transformar el conocimiento que posee de manera que sean pedagógicamente poderosos. Esta caracterización se pone de manifiesto en la redacción que distingue entre saber algo de matemáticas para sí mismo, con la finalidad de poder ayudar a otra persona a aprenderlo. Como indica Shulman (1986), el exponer ideas a los alumnos implica representarlas en forma de analogías, ilustraciones, ejemplos, explicaciones y demostraciones. Esto incluye el uso de ejemplos para ayudar a la formación de conceptos para demostrar los procedimientos, y la selección de actividades para los estudiantes.

Categoría 3. Conexión. Se refiere a la coherencia en la planificación o la enseñanza que se muestra a través de un episodio, una clase o una serie de clases. La Matemática es notable por su relación como un cuerpo de conocimiento y un campo de investigación. La mente del maestro y su gestión a través del discurso matemático en el aula, la concepción de la coherencia incluye la secuenciación de los temas de instrucción dentro y entre las clases, incluyendo el orden de tareas y ejercicios. En gran medida, estos reflejan las decisiones que implican no sólo el conocimiento de las conexiones estructurales dentro de las matemáticas mismas, sino también el conocimiento de las demandas cognitivas relativas a diferentes temas y tareas.

^{Parra-Sandoval (2018}) propone cinco tipos de conexiones: intraconceptual, interconceptual, temporal, interdisciplinar y extracurricular. Las intraconceptuales, se refieren a las conexiones asociadas a un mismo concepto matemático. Las interconceptuales son aquellas relaciones que se establecen entre diferentes conceptos matemáticos y las temporales se establecen entre los diferentes conceptos matemáticos trabajados de acuerdo a los niveles educativos; es decir, con los conceptos matemáticos anteriores y posteriores a él, presentes en el currículo escolar.

La conexión interdisciplinaria significa la relación de un concepto matemático con otras disciplinas del currículo, mientras que las extracurriculares hacen referencia a las conexiones de los conceptos matemáticos con aquellos conocimientos propios de una comunidad de prácticos (conocimientos funcionales) y los conocimientos cotidianos.

Categoría 4. Contingencia. Se refiere a lo que es casi imposible de planificar. Los dos componentes que constituyen esta categoría se derivan de los datos y son la preparación para responder a las ideas de los niños y la preparación en caso de tener que desviarse de la planificación. ^{Shulman (1987}) plantea que la enseñanza generalmente comienza a partir de algún tipo de texto, un programa de estudios, en última instancia, una secuencia de acciones planificadas, destinados a ser llevado a cabo por el profesor dentro de una lección o unidad de algún tipo. Mientras que el estímulo para la enseñanza de los profesores puede ser planificado, algunas de las respuestas de los estudiantes no se pueden prever.

El marco conceptual de ^{Rowland et al. (2005}) introduce un instrumento útil para observar, describir y reflexionar sobre cómo el conocimiento matemático y didáctico del profesor de matemática entra en juego en el aula, es decir, cómo lo implementa en su práctica de enseñanza.

Con relación a lo anteriormente expuesto se realizó una investigación que condujo a este artículo, el cual tiene como objetivo describir el proceso de enseñanza de la función exponencial mediante un acercamiento cualitativo; para ello se estableció una vinculación con el modelo del cuarteto de conocimiento propuesto por ^{Rowland et al. (2005}).

Metodología

El presente estudio se realizó mediante un enfoque cualitativo, y su carácter inductivo permitió al investigador el desarrollo de conceptos, categorías y comprensiones partiendo de la información obtenida en el escenario. En tal sentido, la pretensión no fue generalizar los hallazgos, sino lograr describir los procesos de enseñanza de la función exponencial en una institución educativa de Ecuador.

La investigación está enmarcada en un estudio de caso, con una dimensión descriptiva e interpretativa, debido a que se describen, caracterizan o identifican los distintos hechos relacionados con su campo observacional o componente empírico, como es la descripción del proceso de enseñanza de la función exponencial. Desde la perspectiva interpretativa, su finalidad es interpretar y teorizar sobre el fenómeno estudiado, en este sentido, se desarrollan categorías conceptuales para ilustrar o defender presupuestos teóricos, a partir de un análisis inductivo (^{Husén, 1988}).

De acuerdo con lo analizado se observó un caso (un profesor de matemática) y su clase correspondiente al tema función exponencial. Este método permitió observar las características del docente en el contexto de su aula, con el propósito de analizar distintos aspectos de un mismo fenómeno. Nunca hubo la pretensión de alcanzar conclusiones generalizables (^{Martínez, 2006}), sino mostrar en su ambiente natural del aula la praxis pedagógica utilizada cuando desarrolló el tema de las funciones exponenciales para ser analizada en profundidad.

Para el artículo participó un docente de matemática, quien manifestó su disposición. Este profesor pertenece a la planta docente de una Unidad Educativa de Ecuador, cuya modalidad es presencial de jornada matutina y vespertina con nivel educativo de inicial; educación básica y bachillerato, ubicada en la zona: Urbana INEC y cuenta con 3097 estudiantes aproximadamente.

1. Fases del trabajo de campo o ejecución

El trabajo de campo para el desarrollo de la investigación se realizó en dos fases de acuerdo al objetivo planteado.

Fase 1. Inicialmente se realizó un conversatorio con el docente en cuanto a la posibilidad de observar sus prácticas de enseñanza con relación al tema funciones exponenciales. Luego de conseguir su aprobación se procedió a entrar a sus clases como observador; antes de iniciar las grabaciones para el registro de información se hizo el ingreso para familiarizar con el docente y los estudiantes, de esta manera se fomenta un clima de confianza, posteriormente se grabaron las clases correspondientes al tema.

Fase 2. Descripción del proceso de enseñanza de la función exponencial. Para esto se utilizó la técnica de observación no participante; se trascribieron y analizaron las grabaciones obtenidas, es decir, el análisis se realizó después del trabajo de campo, lo cual según ^{Quintana y Montgomery (2006}), concierne principalmente al desarrollo del sistema de codificación.

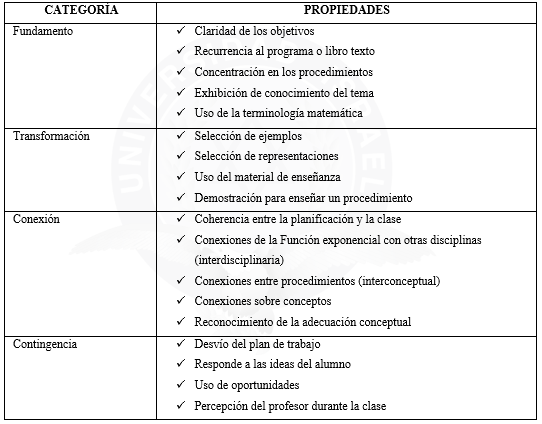
Para esto se realizó el desarrollo del sistema de categorías apriorísticas presentado en la Tabla 1, el cual constituyó el primer paso para la estructuración de la descripción tras la culminación del trabajo de campo. Es de advertir que estas categorías y propiedades fueron provisionales, porque este trabajo constituye una primera entrada y, por tanto, no pueden ser categorías y propiedades definitivas, las mismas pueden cambiar durante el desarrollo de otras investigaciones posteriores.

Tabla 1 Sistema de categorías con relación al objetivo. 

Fuente: elaboración propia (2020)

La información necesaria para la realización del estudio se recolectó a través de videograbaciones y las transcripciones de las clases a las cuales se hizo acompañamiento por medio de la observación no participante.

El análisis e interpretación de los datos cualitativos se realizó en función a las diferentes categorías con sus respectivas propiedades expresadas en la Tabla 1, atendiendo al objetivo formulado en la investigación. Esto permitió hacer manejable el cúmulo de información recogida y presentar los resultados en función del objetivo. El proceso seguido fue el siguiente:

Para la categoría Fundamento se observó si el docente participante tenía claridad de los objetivos que debía cumplir según la programación o planificación; la recurrencia al programa o libro texto como apoyo, la concentración en los procedimientos, su exhibición de conocimiento del tema y el uso de la terminología matemática que él hace durante la clase.

Con relación a la categoría Transformación se hizo énfasis en describir la selección de ejemplos, selección de representaciones, uso del material de enseñanza y la demostración para enseñar un procedimiento por parte de este docente.

Mientras que en la Conexión fue basada en ver la coherencia entre la planificación realizada por el docente y la clase dada, las conexiones de la función exponencial con otras disciplinas, los vínculos entre procedimientos, entre conceptos y el reconocimiento de la adecuación conceptual por parte del docente.

Por último, para la categoría Contingencia se observó la preparación para responder cuando ocurre por alguna causa un desvío del plan de trabajo, cómo responde a las ideas del alumno, el uso de oportunidades y la percepción del profesor durante la clase.

Resultados

Para la descripción del proceso de enseñanza de la función exponencial de este docente se estableció una vinculación con el modelo del cuarteto de Conocimiento propuesto por ^{Rowland et al. (2005}), a través de este se pudo observar los conocimientos matemáticos y didácticos puestos en práctica mediante el apoyo del sistema de categorías de la Tabla 1.

Antes de entrar en detalle con cada categoría, es pertinente hacer una descripción general del proceso de enseñanza que utilizó el caso de estudio. El inicio de su actividad dentro del aula se realiza con puntualidad, manteniendo un clima de respeto y disciplina en el salón. Comienza con un saludo y el establecimiento de normas y pautas, como por ejemplo: “cuando el profesor está explicando no deben revisar el libro, porque a la final no van a atender al libro, ni van a atender al profesor”. Posteriormente da inicio a la explicación del tema, haciendo uso del pizarrón como su único recurso. A continuación, se hace la descripción según las categorías apriorísticas establecidas.

Conclusiones

Como consideración final e implicaciones derivadas de esta investigación, se tiene que la forma tradicional conductista de realizar la praxis pedagógica, caracterizada por el trabajo mecánico y repetitivo al enseñar conocimientos específicos aún se puede apreciar en Ecuador, así lo evidencian los resultados, en concordancia con lo de ^{Avendaño (2013}); ^{Bravo et al., (2017}) y ^{Suárez (2019}). Es importante resaltar que la conexión de la función exponencial con otras disciplinas no se logró del todo, dejando a un lado la importancia de la vinculación de este tema con muchas actividades humanas relacionadas con la economía, biología, física, química, demografía, entre otras.

Al describir el proceso de enseñanza del tema tratado en una institución del Cantón Santo Domingo de los Colorados en Ecuador se concuerda con lo expuesto por ^{Parra-Sandoval (2018}), quien opina que es necesario explorar el trabajo interdisciplinario como espacio privilegiado para ampliar el conocimiento profesional que permite al profesor conectar un conocimiento matemático con otros conocimientos y saberes u otras áreas curriculares.

Los resultados de este estudio vislumbran la necesidad urgente de promover cambios en la praxis educativa de los docentes en ejercicio, lo cual puede ser a través de procesos de formación efectivos, con seguimiento y acompañamiento, lo cual representa un reto debido a que esto implica el desarrollo de competencias profesionales que le permitan al profesor de matemáticas vincular las matemáticas con otras realidades, esto conlleva a que se propongan nuevas formas de dinamizar e intervenir en ambientes escolares con temas matemáticos que pueden vincularse a algunas actividades humanas y así lograr que sus estudiantes se interesen más por lograr aprendizajes sobre las funciones exponenciales, como tema de gran importancia por sus aplicaciones a otros campos.