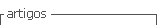Introduction
Complex problems require powerful tools to analyze and process a considerable amount of data. Scientists and engineers have difficulties solving problems with repetitive and independent calculations. Therefore, it is necessary to parallelize the calculation processes. For this purpose, the Central Processing Unit (CPU) and Graphics Processing Unit (GPU) can be used. A CPU has multiple cores and allows processes to be carried out in parallel. However, a GPU has a more significant number of cores. Therefore, it is often used in high-performance computing (HPC) problems (Domínguez, Crespo, and Gómez-Gesteira 2013).
At first, the GPU objective was image processing, video game execution, and development, and now the applications include HPC. A GPU is considered a massive parallel processor with considerable memory bandwidth. The GPU has a set of hierarchically organized memories that can be used at the programmer's convenience. However, several scientific articles propose a heterogeneous use, which means complementing the work of the GPU with the CPU for better performance (Knepley and Yuen 2013; Teodoro et al. 2009). The GPU has been helpful in some projects, such as the simulation of artificial systems, artificial neural networks, bioinformatics, and meta-heuristic optimization algorithms. Each of them can grow in complexity due to multiple similar calculations.
On the other hand, optimization is an area of mathematics that seeks methods and formulations that allow finding the maximum or minimum values in an objective function. These values are considered optimal global solutions within a search space if the problem can be represented using a convex formulation. The most common areas of optimization applications are engineering, economics, and manufacturing. Meta-heuristic algorithms have been recognized in the optimization area as powerful tools (Kurniasih, Utami, and Raharjo 2019; Van Luong, Melab, and Talbi 2011; Sapra, Sharma, and Agarwal 2017). Even when these algorithms cannot guarantee optimal global solutions, they effectively solve non-convex problems, providing at least good quality solutions. Therefore, in this research, the Particle Swarm Optimization (PSO) meta-heuristic algorithm will be used to improve its performance (measured in execution time) using the GPU hardware tool.
Additionally, in electric power engineering, the classic TEP problem meets the characteristics to be evaluated. The main objective of the TEP problem is to determine the necessary changes in the transmission system infrastructure. These changes must allow for satisfying the demand with the power supply efficiently. Also, TEP is considered a mixed-integer, combinatorial, nonlinear complex problem. Therefore, it is expected to find some local optima. The TEP seeks to obtain, among several candidate topologies, one that can meet the demand of the electricity grid as long as this represents the least cost related to infrastructure. Several researchers have tried to solve this problem through meta-heuristic algorithms, obtaining promising results (Rodriguez, Falcão, and Taranto 2008; Torres and Castro 2012, 2014; Verma, Mukherjee, and others 2016).
Hence, matrix operations, the Travelling Salesman Problem (TSP), and the TEP problem are presented as case studies. Thus, in the TEP problem, the feasibility of using the GPU in a real problem is analyzed.
This paper is organized as follows: Section 2 contains the related works on which this research has been based. Section 3 shows a theoretical evaluation of the algorithms and models involved. Section 4 shows the tools that will be tested and used for implementation. Section 5 shows the performance results obtained by testing the tools and implementing the meta-heuristic algorithm. Finally, Section 6 shows the conclusions and recommendations for future research.
Background
Particle swarm optimization
The particle swarm optimization (PSO) is one of several algorithms that have been analyzed to optimize the TEP problem (Lambert-Torres et al. 2008; Trelea 2003). Algorithm shows the basics of the PSO algorithm. This algorithm is based on the movement of bees when they search for food. The entire swarm communicates and shares information. If a bee finds food, it sends the information to the other bees. Consequently, all the swarms will go to that place. In the planning of an electrical network, each bee represents a randomly created topology. Evaluating all the created topologies allows for finding the optimal temporal topology. The other topologies will be recreated based on the optimal temporal topology until a better one is found. Finally, the search ends after a certain number of iterations.
PSO considers each of the candidate topologies as a particle. These particles have their position and speed. When evaluating the set of particles, the best one is found, and each particle evolves according to that particle, changing its position and speed. The speed and position are expressed in equation ( 1 ) and equation ( 2 ), respectively.
( 1 )
( 2 )
Table 1: Algorithm 1: PSO - Meta-heuristic algorithm.
| Algorithm 1 |
| Input: initial topology Output: best topology 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: Initialization of random positions Initialization of random speeds while Stop criteria do for i in each particle do Update particle speed Vi(t + 1) = Vi(t) + c1 × r1 × (Pibest − Pi(t))+ c2 × r2 × (Pg best − Pi(t)) Update particle position Pi(t + 1) = Pi(t) + Vi(t + 1) Update better personal position Update better global position Best overall as a result |
(Table 1)Speed and position are the essential equations of the algorithm. Therefore, the mathematical operations performed on both equations should be optimized. The fundamental operations in the PSO algorithm equations are matrix addition and multiplication. However, several researchers point to better efficiency and less execution time for matrix operations. However, it is necessary to test the tools to execute the algorithms on the GPU; this is shown in Section 4.
Meta-heuristic parallelization
Parallelization is useful for meta-heuristic algorithms that create a population of possible solutions, such as the PSO algorithm. The main objective is to speed up the search process, improve the solution obtained, and give the meta-heuristics robustness. By parallelizing, the number of particles evaluated can be increased without affecting the available computational capacity.
The parallelization of the equations ( 1 ) and ( 2 ) allows updating the speeds and positions of the swarm in less time. On the other hand, equation ( 3 ) is described as the objective function of the problem TEP. Thus, when reviewing its structure, it is notable that the ω value results from the PET operational problem and cannot be parallelized since it depends directly on the tool that evaluates the load disconnection of the topology. Therefore, the general parallelization diagram of the meta-heuristic PSO is shown in Figure 1.
TEP model
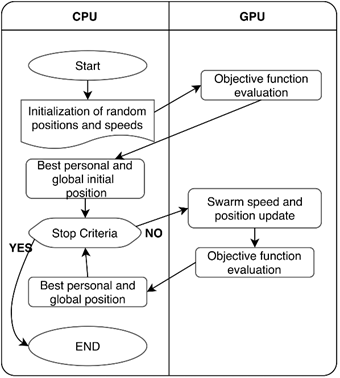
When evaluating the topology, several parameters must be considered. Therefore, analyzing reactive power considered in the AC model will be pretty helpful. The AC model allows for finding a better solution than the DC model. Therefore, the topology found is more electrically efficient because of the parameters considered in the AC model. The AC model can be divided into two problems: expansion problem and operational problem.
The expansion problem involves all those restrictions that the candidate topologies must meet. The evaluation function is strictly associated with the costs of transmission lines in the topology and the number of lines that can be added to satisfy the electrical demand. Additionally, a penalty should be considered if the topology does not converge. Equation ( 3 ) shows the relationship between the mentioned parameters.
( 3 )
Subject to
On the other hand, the operational problem refers to the load disconnection evaluation of one topology to find out if the existing generators and transmission system do not satisfy the demand; as a result, a ω value is obtained. If the evaluation does not converge, ω takes a high value, so the topology is not considered. Matpower is one of the most common and has been used in various research (Zimmerman, Murillo-Sánchez, and Thomas 2010). However, in this work, Pandapower executes the optimal flow. This tool allows the building of a fully modifiable network. The evaluation function, belonging to Pandapower, provides the load disconnection cost when executing the optimal power flow. The evaluation function takes into account: load flow equation, branch constraints, bus constraints, and operating power constraints (Lezama and Pareja 2008). The interaction between the expansion problem and the operational problem is shown in Figure 2.
Related Works
A GPU is constantly used in projects that need performance improvement, or its execution time must be minimal. Processes in which a large amount of data needs to be computed in parallel. In a wide variety of research, using a GPU has been the solution. Projects that usually used a CPU are now being executed through a GPU (Anzt et al. 2010). Communication between the user and the GPU is possible due to the Application Programming Interfaces (APIs). Compute Unified Device Architecture (CUDA) is a platform that interfaces between the user and the GPU hardware unit. An additional programming language is required to use CUDA, the most common are Fortran, C++, and Python (Anzt et al. 2010). Although the use of a GPU seems simple, its integration can be complex in specific problems. Transferring data between the CPU (host) and the GPU takes time. Therefore, its use may be limited to some instances (Sunitha, Raju, and Chiplunkar 2017).
In previous research, the use of a GPU for the execution of meta-heuristic algorithms has been positive. These algorithms can be relatively easy to implement and are used for many problems with many possible candidate solutions. Meta-heuristic algorithms such as ant colony (ACO) and particle swarm (PSO) have been tested and optimized for specific problems (Bonate and Howard 2013; Dorigo and Stützle 2003; Nebro et al. 2009). TSP is a clear example where any of the algorithms mentioned can be used (Lin 1965). The TSP is based on a list of cities to which a seller must go; each city must be visited only once, and with the shortest distance traveled, finally, the seller must return to the first city visited. The use of meta-heuristics facilitates evaluating a certain number of possible solutions, reaching the desired response with the shortest distance traveled. Therefore, in these types of problems, it has been essential to translate the meta-heuristics into a language supported by a GPU, to obtain accurate and fast solutions (Souza et al. 2011).
On the other hand, the TEP problem has several methods of solution. On the one hand, the DC model is commonly used because it does not consider reactive power analysis, making it less complex. On the other hand, the AC model considers the analysis of reactive power, making it a non-linear and exact model. So far, there is not much research on using meta-heuristic algorithms that consider the AC model to provide a solution to TEP. PSO has proven to be one of the few valuable algorithms in this problem, and it is described in (Fonseka and Miranda 2004; Matute et al. 2020; Morquecho et al. 2020; Morquecho, Torres, and Castro 2021; Torres and Castro 2012, 2014).
Methodology and implementation
As a first stage, the programming language to be used with CUDA was selected. The languages that can be used are Python, C++ and Fortran. Python was chosen because it is considered one of the most powerful tools today (Dogaru and Dogaru 2015). In addition, Python is compatible with CUDA and has a wide variety of libraries that allow it to communicate with the GPU. In the second stage, the available libraries were analyzed, of which three outstanding ones were obtained: Cupy, Numba, and Theano. Of the selected libraries, the library with the best performance in terms of the execution time was sought.
Additionally, the library dedicated to scientific calculations of Python known as Numpy was taken into account; this served as a benchmark for CPU performance (Oliphant 2006). The tools used to connect to the GPU via CUDA were: numba 0.5, cupy 7.6.0, and theano 1.0.5. All of these are compatible with version 3.7 of Python. Instead, the numpy 1.16 library was used as a benchmark for CPU performance. After evaluating all the libraries, we decide to use the Cupy library to optimize the algorithms through the GPU. In the third stage, A CUDA-compliant programming language and software capable of solving the TEP operational problem using the AC model were required. Finally, with the selected tools, the PSO meta-heuristic algorithm focused on solving the PET problem was programmed. For reproducibility purposes, the source code is shared in Github (https://github.com/fabianastudillo/GPUOptimizationMetaheuristics.git).
Python and CUDA
Python supports several libraries that allow the use of the GPU through the CUDA platform. The most outstanding libraries are: ``Numba'', ``Cupy'', ``Theano'' (Al-Rfou et al. 2016; Lam, Pitrou, and Seibert 2015; Preferred Networks and Preferred Infrastructure 2018). To compare the performance of a CPU versus a GPU, the scientific calculation library ``Numpy'' and the Matlab software have been chosen. Numpy and Matlab contain highly optimized, and high-level mathematical functions (Oliphant 2006).
The method for comparing libraries is simple: multiplication and addition of square matrices element by element is required. The computational complexity increases exponentially as a function of the matrix dimensions. It has been chosen the library that executes the matrix operations in less time than the others (Crist 2016).
Numba: It is an open-source just-in-time (Jit) compiler; this means that part of the Python code and the Numpy library is translated into a low-level language. It supports using graphics processing units (GPUs) through the CUDA platform. Also, the Numba tool has decorators or function identifiers with different characteristics. Most of these functions can be performed on the CPU, and GPU (Oliphant 2006).
Theano: This compiler allows a GPU to speed up calculations, parallelizing processes across the multiple cores and threads that a GPU integrates (Al-Rfou et al. 2016).
Cupy: It is a GPU-accelerated open-source library using the CUDA platform. This library is designed to be fully compatible with Python. What makes Cupy unique is its user interface, similar to Numpy; this means that a large percentage of Numpy functions are available on Cupy (Preferred Networks and Preferred Infrastructure 2018).
TEP model and Pandapower
The TEP problem using the AC model can be implemented using the Pandapower software tool. Pandapower runs the optimal flow on any electric network. First, network elements are created with functions that belong to this software. Each network element has specific adjustable parameters according to the analyzed network (Thurner et al. 2016). The Garver-6 bus test system has been selected to perform the test suite. This model will share the characteristics of each element shown in (Torres and Castro 2012).
PSO meta-heuristic and TEP problem
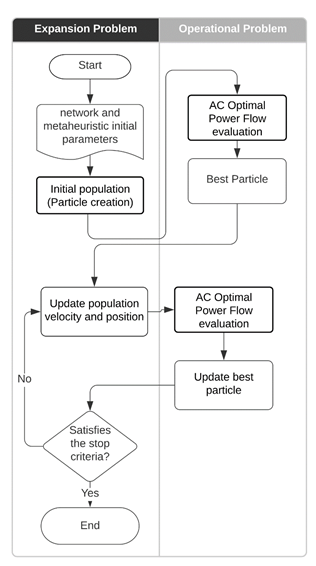
The meta-heuristic PSO algorithm is focused on treating the expansion problem. For this, each candidate topology is called a particle. The initial population is arranged in a 𝑚 ×𝑛 matrix. Where 𝑚 is the number of initial particles, and 𝑛 is the dimension of the TEP problem, which depends on the number of available paths that can add a circuit; in this case, 15 for the 6-node Garver system. The resulting 𝑚×𝑛 matrix is shown in Figure 3.
Experimental result
The results were obtained by running tests on an Acer Predator Helios 300 computer with an i7-8750h central processing unit (CPU), GTX-1060 graphics processing unit (GPU), and 16 GB of RAM. In the “library comparison” section, the pre-selected software tools are evaluated using matrix addition and multiplication operations. Time was chosen as a parameter for comparison between libraries. Then, in the “Meta-heuristic and Cuda” section, the PSO meta-heuristic algorithm was implemented using only the CPU and another version that incorporates the GPU; this implementation is used to solve a two-dimensional problem, where the number of particles and iterations are scaled independently until obtaining a difference in performance. Implementing the PSO algorithm with the help of the GPU was done using the tool chosen in the library comparison section. Finally, the full implementation of the TEP problem was made using the PSO algorithm and the library chosen to run the code on the GPU.
Library comparison
The library comparison reflects the runtime performance among the selected software tools to accelerate GPU processes. The multiplication and the sum of a matrix, element by element, allow knowing the performance of each library. The number of processes will increase with the array's size, and consequently, the runtime will change. The library comparison does not fully evaluate the meta-heuristic algorithm, only the matrix operations of equations ( 1 ) and ( 2 ); this is because the parallelization is according to the Figure 1.
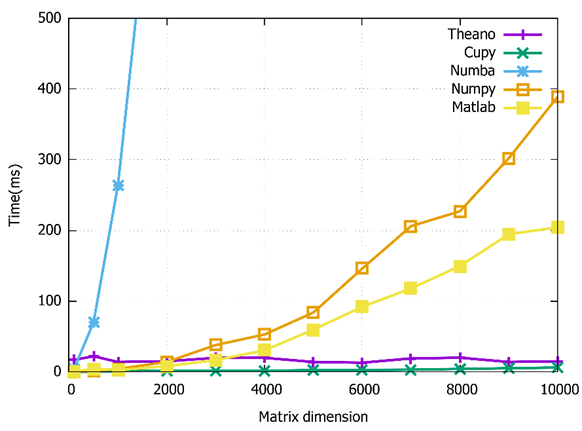
Figure 4 shows the execution times of the multiplication of square matrices. The dimension of the matrices starts at 100×100 up to a dimension of 10000×10000. The Cupy library has the lowest execution time for each multiplication operation.
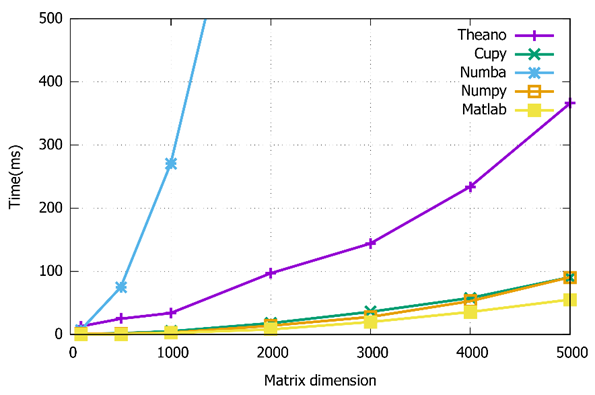
On the other hand, Figure 5 shows the execution times of the addition operation. The dimension of the matrices, in this case, increases from 100×100 to 5000×5000. According to the results, the Cupy and Numpy libraries have similar execution times. Therefore, the “Cupy” library performs optimally in both matrix operations. Consequently, Cupy is used as the primary tool to implement the meta-heuristic algorithm in the next section.
Meta-heuristic and CUDA
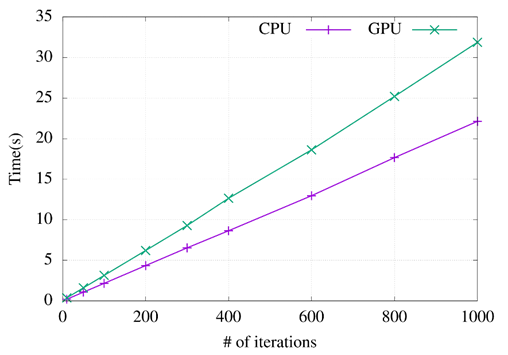
In this section, TSP has been implemented using the PSO meta-heuristic algorithm. This problem is 2-dimensional. In this test, two parameters are modified: the iteration's number and the particle's number. Figure 6 and Figure 7 show the comparison of runtimes between a CPU and a GPU. Figure 6 shows the runtimes based on the iteration's number (from 10 to 1000), the particle's number is fixed at 40.
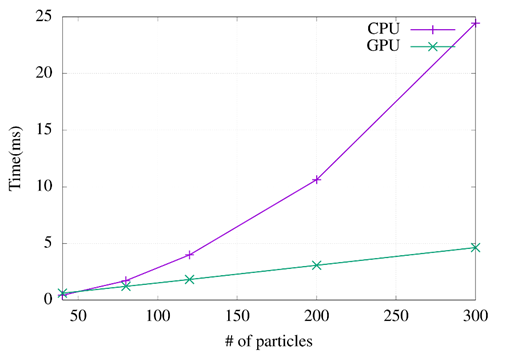
Furthermore, Figure 7 shows the runtimes based on the particle's number (from 40 to 300), the iteration's number is fixed to 20.
Increasing the particles in a meta-heuristic contributes a lot; a better solution can be found with a more significant number of candidate solutions analyzed. In this case, the use of GPU is a significant help. The results indicate an increase in particles and a shorter execution time than the algorithm developed in the CPU. For this reason, the GPU has been considered a great alternative to improve the performance of the TEP.
TEP performance
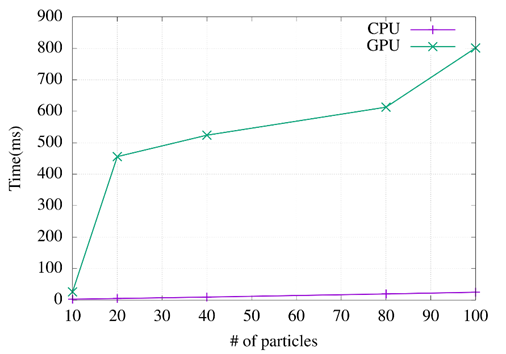
The TEP problem was programmed using the Pandapower library. The PSO meta-heuristic algorithm was programmed to optimize the TEP problem through Cupy. In this case, the objective function of the TEP problem was not parallelized because it depends directly on the Pandapower tool, and it can only be executed sequentially. In the TEP problem, the particle's number was considered as the comparison parameter. The particle's number ranged from 10 to 100. Additionally, out of many models available, the Garver 6-bus test system has been selected to be evaluated.
The comparison results between the CPU and the GPU are shown in Figure 8. The GPU in the TEP problem does not represent a positive contribution due to the incorporation of random values in the meta-heuristic velocity equation. It is necessary to access the elements with matrix indexing to carry out this process. Unfortunately, for the libraries available in Python this function is not optimized. Therefore, the runtime is affected.
The TEP's operational problem has been compared to (Torres and Castro 2012). Matpower tool is replaced by the Pandapower tool. Pandapower is more flexible and easier to program than Matpower. Pandapower offers functions that allow creating a network from scratch, adding and removing parameters according to requirements. However, evaluation time is compromised. Topologies must be created one by one with Pandapower's pre-established functions; this considerably slows down the evaluation process. Unlike Matpower, which can quickly change the structure of the topology.
Conclusions
In this work, using GPU to improve the runtime of the meta-heuristic algorithms has been presented. The process starts with testing and comparing libraries that allow running code on the GPU; then, implementing the meta-heuristic algorithm with the best library. Finally, the PSO meta-heuristic algorithm was proved in two different dimension problems.
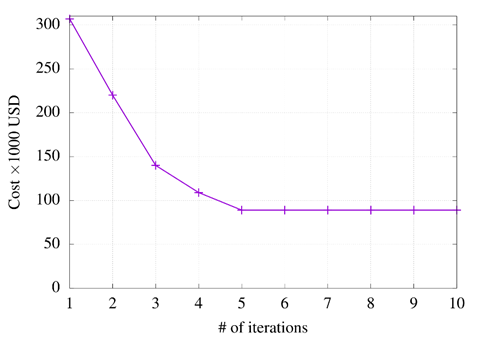
In the results, the GPU helped solve the TSP. Because more solutions or candidate particles were analyzed in less time. On the other hand, according to the results obtained, it is assumed that there would be a better performance in solving the TEP problem by using the GPU and analyzing a more significant number of candidate topologies in less time. However, this was not the case; according to the results shown in Figure 9, the use of the GPU takes a longer time when analyzing more particles. Therefore, it is necessary to analyze the structure of algorithms and how mathematical operations interact in the GPU for problems of over two dimensions; this is because the indexing of matrix operations is not well optimized for the GPU in current software tools.
Another cause of the slowdown is communication between CPU and GPU functions. Certain functions are not available to the GPU, such as matrix transposition, creating randomized values, and getting minimum values in a matrix or array, so it is necessary to use existing functions in the CPU. In addition, transferring data between these hardware units does not contribute to the decrease in execution time.
Although Python has proven to be an excellent alternative to execute code on the GPU through multiple libraries and is an easy programming language, it is recommended to consider other languages. One of the most recommended options is C++, which is compatible with CUDA. Also, the code is similar to machine language, and it is possible to define the kernel.
In the future, a thorough evaluation of the tools that calculate the cost per load disconnection in an electrical transmission system is necessary to parallelize internal processes.