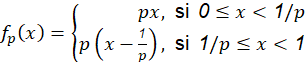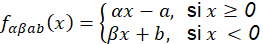Introducción
Uno de los primeros estudios de la dinámica de transformaciones lineales por partes (o a trozos) comenzó con (Rényi, 1957) mostrando que la siguiente aplicación (ecuación 1) preserva una única medida ergódica equivalente a la medida de Lebesgue para 𝑝>1.
Más tarde Parry en su trabajo (W. Parry, 1964) generaliza la transformación de Rényi considerando 𝑇 𝑥 = 𝛽𝑥+𝛼 mod1, mostrando también que 𝑇 preserva una única medida ergódica equivalente a la de Lebesgue para 𝛽>1. Posteriormente Wilkinson en (Wilkinson, 1974) generaliza el trabajo de Parry. A partir de este trabajo se generalizó para funciones crecientes por parte en un intervalo compacto, ver (Boyarsky & Góra, 1997). Es bien conocido que la dinámica de una trasformación sobre un espacio de fase no acotado o no compacto se comporta diferente al caso acotado. Una pregunta natural es: Como es la dinámica de una transformación lineal por partes sobre ℝ? En respuesta a esta pregunta, en (NUSSE & YORKE, 1995) ycon mayor detalle en (Jain & Banerjee, 2003) estudió la transformación lineal por partes 𝑓 𝛼𝛽𝑎𝑏 : ℝ→ℝ definida en la ecuación 2 como un caso unidimensional, para determinar la existencia de bifurcación de colisión de frontera esto es, una bifurcación que ocurre cuando un punto fijo (o una órbita periódica), a medida que se mueve el parámetro, cruza o colisiona con la frontera entre las dos regiones de comportamiento suave.
Estos dos trabajos dieron inicio al estudio de esta familia a 4 parámetros. El caso de los parámetros −𝑎≤𝑏<0 la dinámica es simple y puede aparecer hasta dos puntos fijos atractor o repulsor. También se puede ver el itinerario de las órbitas cuando va de la componente conexa positiva a la componente conexa negativa de ℝ∖{0} ver (Rajpathak et al., 2012). El caso 𝛼>1 y 𝛽>1 es estudiado por (Rajpathak et al., 2015) probando que existe una órbita caótica y describen el comportamiento de las órbitas periódicas estables, en ese mismo trabajo se menciona la existencia de una región atractora pero no indica exactamente sus dimensiones. En (Avrutin et al., 2014) analizan y estudian numéricamente las bifurcaciones del atractor para diferentes valores del parámetro de 𝑓 𝛼𝛽𝑎𝑏 . En (Avrutin et al., 2006) realizan un estudio de otro tipo de bifurcaciones (bifurcaciones de codimensión 2 y codimensión 3) que aparecen en la transformación 𝑓 𝛼𝛽𝑎𝑏 con 𝑎=𝑏. Recientemente en (Du et al., 2018) estudia numéricamente el atractor también. En todos estos trabajos mencionados anteriormente ninguno identifica exactamente el conjunto atractor. Tampoco se identifica con las regiones en el espacio de parámetros donde 𝑓 𝛼𝛽𝑎𝑏 exhibe un conjunto atractor no trivial, es decir que no sea un punto fijo, una órbita periódica o una unión finita de órbitas periódicas. Hasta el momento no hay un estudio sobre las medidas ergódicas que pueden estar soportadas sobre el atractor. En este trabajo se da respuesta positiva a todas estas interrogantes.
En este trabajo se considera los parámetros 𝛼>0, 𝛽>0, 𝑎>0 y 𝑏>0. Se prueba exactamente para que valores del parámetro el conjunto 𝐴=[−𝑎, 𝑏) es atractor. También se identifica los valores del parámetro donde el atractor 𝐴 es caótico (la dinámica de 𝑓 𝛼𝛽𝑎𝑏 restricto a 𝐴, denotada por 𝑓 𝐴 , posee una órbita densa en 𝐴). Inclusive se prueba que si 𝑓 𝛼??𝑎𝑏 −𝑎 = 𝑓 𝛼𝛽𝑎𝑏 (𝑏) con 𝛼=1 y 𝛽=1 la dinámica del atractor se comporta exactamente como la rotación de Poincaré del círculo unitario, en este caso se prueba que si 𝑎 𝑏 es racional e irreducible entonces, todos los puntos de 𝐴 son periódicos de periodo 𝑎+𝑏, y si 𝑎 𝑏 es irracional entonces, la órbita de todos los puntos de 𝐴 es denso en 𝐴. También, se muestra los valores del parámetro donde el atractor es global, es decir, todas las órbitas de los puntos de la recta real ℝ son atraídos por el conjunto 𝐴. Además, se prueba los valores del parámetro donde 𝑓 𝛼𝛽𝑎𝑏 restricto a 𝐴 posee una medida invariante absolutamente continua a la medida de Lebesgue y valores del parámetro donde 𝑓 𝛼𝛽𝑎𝑏 restricto a 𝐴 admite una medida equivalente a la medida de Lebesgue.
Es importante destacar que las funciones continua lineales por partes aparecen como modelos matemáticos en muchos sistemas prácticos de ingeniería eléctrica (Banerjee & Verghese, 2001). Además, también aparece como modelo para describir fenómenos en Ciencias Física y Economía, según (Tramontana & Gardini, 2011). Recientemente (Belyaev & Ryazanova, 2019) estudian el atractor que aparece en una familia de funciones lineales por parte como un modelo de actividad neuronal.
El capítulo 3 de resultados, está organizado en dos secciones. En la sección 3.1 se estudia la existencia del atractor y se identifica exactamente la región de los parámetros para los cuales 𝑓 𝛼𝛽𝑎𝑏 exhibe a 𝐴=[−𝑎, 𝑏) como atractor. En la sección 3.2 se estudia la dinámica del atractor primero el caso en que 𝑓 𝐴 es biyectiva y luego el caso en que los parámetros satisfacen la condición 𝑓 𝛼𝛽𝑎𝑏 −𝑎 < 𝑓 𝛼𝛽𝑎𝑏 (𝑏) para analizar la existencia de medidas invariantes.
Metodología
La metodología lógico-deductiva que forma parte ineludible de la investigación en matemática fue usada para aplicar teoremas generales sobre transformaciones continuas por partes definidas sobre un intervalo compacto al modelo estudiado de funciones lineales crecientes por partes bajo la existencia del atractor 𝐴.
Los objetivos fueron alcanzados de la siguiente forma: primero, identificar la forma topológica del atractor e identificar exactamente los parámetros donde la transformación 𝑓=𝑓 𝛼𝛽𝑎𝑏 para alcanzar esto se implementó la condición en los parámetros: −𝑎≤𝑓 −𝑎 ≤𝑓 𝑏 ≤𝑏. Note que, si 𝑓(−𝑎)>𝑓(𝑏) entonces, el candidato a atractor, el intervalo 𝐴, satisface que 𝑓(𝐴)⊈𝐴 y esto implica que 𝐴 no sea atractor.
El segundo objetivo es estudiar la dinámica del atractor según los parámetros de la familia 𝑓. El primer caso se concentra cuando 𝑓 𝐴 ( 𝑓 restricto a 𝐴) es biyectiva en este caso usamos la teoría existente sobre homeomorfismos del circulo unitario cuya conexión con la familia a 4 parámetros en estudio se hace mediante una conjugación topológica, ya que la conjugación topológica permite identificar dinámicas equivalentes. El segundo caso correspondiente a la existencia de medidas invariantes absolutamente continuas a la de Lebesgue el objetivo es conseguido aplicando teoremas existentes sobre la transformación del Lorenz unidimensional sobre un intervalo compacto.
Resultados
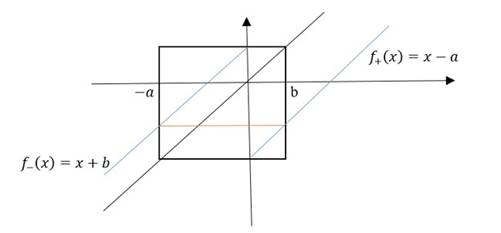
Considere la función 𝑓 𝛼𝛽𝑎𝑏 : ℝ→ℝ definida por
donde 𝛼>0, 𝛽>0, 𝑎>0, 𝑦 𝑏>0. Para facilitar el lenguaje en este capítulo se considera la siguiente notación: 𝑓= 𝑓 𝛼𝛽𝑎𝑏 , 𝑓 − = 𝑓| (−∞, 0) , 𝑓 + = 𝑓| (0, +∞) y 𝐴=[−𝑎, 𝑏). Para el estudio de la dinámica de 𝑓 según los parámetros se necesita lo siguiente:
Condición 1. −𝑎≤𝑓(−𝑎)≤𝑓(𝑏)≤𝑏.
Esta condición es necesaria para probar la existencia del atractor 𝐴.
Existencia del Atractor
Definición 3.1 Un conjunto Λ es un atractor para 𝑓 si, 𝑓 Λ =Λ y existe un conjunto abierto 𝑈⊂ℝ con Λ⊂𝑈 tal que 𝑑(𝑓 𝑛 𝑥 , Λ)→0 cuando 𝑛→+∞. Al conjunto de puntos 𝑥∈ℝ tal que 𝑑(𝑓 𝑛 𝑥 , Λ)→0 cuando 𝑛→+∞ se denomina cuenca de atracción de Λ y de denota por 𝐵 Λ . Λ es un atractor global para 𝑓 si, Λ es un atractor y 𝐵 Λ =ℝ. Aquí 𝑑(𝑥,𝑦)=|𝑥−𝑦| para todo 𝑥,𝑦∈ℝ.
Debido que la función 𝑓= 𝑓 𝛼𝛽𝑎𝑏 no es continua, la definición de atractor considerada aquí difiere con la definición clásica, como por ejemplo la considerada en (Milnor, 1985). En este caso el atractor no es cerrado.
Definición 3.2 Un conjunto A⊂ℝ es un atractor topológico para 𝑓 si, A es un atractor y 𝑓 𝐴 =𝑓| 𝐴 es transitivo.
Lema 3.3 Si 𝑓 satisface la condición 1 entonces, 𝑓 𝐴 =𝐴.
Demostración. Observemos primero que, como 𝛼>0 y 𝛽>0, la función 𝑓 es creciente en cada componente conexa (−∞, 0) y (0, +∞). Sea 𝑦∈𝑓 𝐴 entonces, existe 𝑥∈𝐴 tal que 𝑦=𝑓 𝑥 . Como 𝑥∈𝐴 se tiene que 𝑥∈ −𝑎,0 𝑈(0,𝑏). Si 𝑥∈ −𝑎,0 por definición de 𝑓 implica que, 𝑓 𝑥 =𝛽𝑥+𝑏. De esto y la condición (1) se tiene que, −𝑎≤𝑓(𝑥)<𝑏 por tanto 𝑦∈𝐴. Si 𝑥∈(0, 𝑏) por definición de 𝑓 𝑥 =𝛼𝑥−𝑎, esto junto a la condición (1) implica que −𝑎≤𝑓(𝑥)<𝑏 y esto significa que 𝑦∈𝐴. Por tanto 𝑓(𝐴)⊂𝐴.
Note que si 𝑓 satisface la condición 1 y 𝑓 𝑏 =𝑏 entonces, en este caso particular 𝑓 𝐴 = 𝐴 . Por tanto 𝐴 , la clausura de 𝐴, también, es atractor.
Observación 3.4 Suponga que 𝑓 satisface la condición 1.
Si 𝛼<1, entonces 𝛽>1;
Si 𝛽<1, entonces 𝛼>1.
Lema 3.5 Suponga que 𝑓 satisface la condición 1.
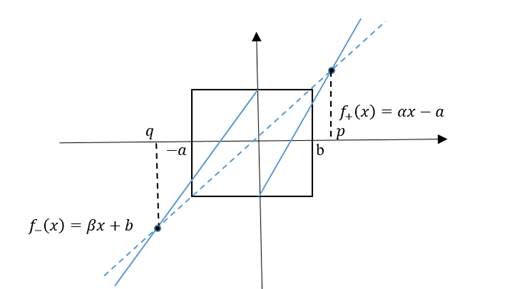
Si 𝛽>1, entonces existe un punto fijo 𝑞, con 𝑞≤−𝑎, tal que 𝑓 𝑛 (𝑥)→−∞, 𝑛→+∞, para todo 𝑥<𝑞. Ver figura 1.
Si 𝛼>1, entonces existe un punto fijo 𝑝, con 𝑝≥𝑏, tal que 𝑓 𝑛 𝑥 →+∞, 𝑛→+∞ para todo 𝑥>𝑝. Ver figura 1.
Demostración. Caso a) Si 𝛽>1, esto implica que 𝑓 − tiene un punto fijo 𝑞, que por la condición 1, 𝑞≤−𝑎. Además, 𝑓(𝑥)<𝑥 para todo, 𝑥<𝑞. Como 𝑓 − no tiene puntos fijos en (−∞, 𝑞), por tanto que 𝑓 𝑛 (𝑥)→−∞, 𝑛→+∞, para todo 𝑥<𝑞. El caso b) es análogo púes, por el hecho que 𝛼>1 y la condición 1 existe un punto fijo 𝑝 con 𝑝≥𝑏 y 𝑓(𝑥)>𝑥 para todo 𝑥>𝑝.
El siguiente resultado da una condición necesaria para identificar cuando 𝐴=(−𝑎, 𝑏) es un atractor, además, mostrará que la trayectoria de cada punto de la cuenca de atracción de 𝐴 a partir de una determinada iterada queda contenido en 𝐴.
Teorema 3.6 Suponga que 𝑓 satisface la condición 1. Si −𝑎<𝑓 −𝑎 o 𝑓(𝑏)<𝑏, entonces 𝐴 es un atractor. Además, 𝐵 𝐴 = 𝑈 𝑛≥0 𝑓 −𝑛 (𝐴).
Demostración. Por el lema 3.3, 𝑓 𝐴 =𝐴. Faltaría probar la segunda parte la definición de conjunto atractor (ver definición 3.1). Suponga que −𝑎<𝑓 −𝑎 . Se probará que si 𝛽≤1 entonces, tal que, para todo 𝑥∈ −∞,−𝑎 existe 𝑛≥1 tal que 𝑓 𝑛 𝑥 ∈𝐴. Para ello, sea 𝑥∈ −∞,−𝑎 . Por hipótesis 𝑓 − no tiene puntos fijos y 𝑓 − ′ 𝑥 =𝛽≤1 entonces, 𝑓(𝑥)>𝑥. Al iterar varias veces 𝑓 sobre el punto 𝑥, se sigue que existe 𝑛≥1 tal que 𝑓 𝑛 𝑥 ≥−𝑎 y 𝑓 𝑛−1 𝑥 <−𝑎<0. Por tanto 𝑓 𝑛 ?? <𝑏 y así, 𝑓 𝑛 𝑥 ∈𝐴. Si 𝛽>1, como −𝑎<𝑓 −𝑎 implica que existe un punto fijo 𝑞<−𝑎 y 𝑓(𝑥)>𝑥 para todo 𝑥∈(𝑞, −𝑎). Entonces, iterando 𝑓 varias veces existe 𝑛≥1 tal que 𝑓 𝑛 𝑥 ≥−𝑎 y 𝑓 𝑛−1 𝑥 <−𝑎<0. Por tanto 𝑓 𝑛 𝑥 <𝑏, es decir, 𝑓 𝑛 𝑥 ∈𝐴. Por tanto 𝐴 es un atractor. Ahora, si 𝑓(𝑏)<𝑏 la prueba es análogo al caso anterior. Si 𝛼≤1 se muestra que para todo 𝑥>𝑏, existe 𝑛≥1 tal que 𝑓 𝑛 𝑥 ∈𝐴 y si 𝛼>1 se muestra que existe un punto fijo 𝑞>𝑏 tal que 𝑓(𝑥)<𝑥 para todo 𝑥∈(𝑏, 𝑞). Entonces, iterando 𝑓 varias veces existe 𝑛≥1 tal que 𝑓 𝑛 𝑥 ∈𝐴. Para terminar la prueba sólo falta ver que B 𝐴 = 𝑈 𝑛≥0 𝑓 −𝑛 (𝐴). Claro está que 𝑈 𝑛≥1 𝑓 −𝑛 𝐴 ⊂B(𝐴). Si −𝑎<𝑓 −𝑎 y 𝛽<1, se mostró que −∞, −𝑎 ⊂ 𝑈 𝑛≥0 𝑓 −𝑛 𝐴 , por la observación 3.4, resulta que 𝛼>1, en este caso existe un punto fijo 𝑞, con 𝑞≥𝑏. Si 𝑞=𝑏, entonces por el Lema 3.5 B 𝐴 =(−∞, −𝑏], esto implica que B 𝐴 ⊂𝑈 𝑛≥0 𝑓 −𝑛 𝐴 . Si 𝑞>𝑏 ya se demostró que 𝑏, 𝑞 ⊂ 𝑈 𝑛≥0 𝑓 −𝑛 𝐴 , de aquí y lema 3.5 se tiene que B 𝐴 ⊂𝑈 𝑛≥0 𝑓 −𝑛 𝐴 . Ahora, si 𝑓(𝑏)<𝑏, el razonamiento es análogo. Por tanto, B 𝐴 =𝑈 𝑛≥0 𝑓 −𝑛 𝐴 .
Condición 2. −𝑎<𝑓 −𝑎 o 𝑓(𝑏)<𝑏. Ver figura 2.
De la demostración del Teorema 3.6 se puede extraer el siguiente resultado, que ya había sido observado por (Jain & Banerjee, 2003).
Corolario 3.7 Suponga que 𝑓 satisface la condición 1.
Si 𝛼≤1, entonces, 𝑓 + no posee un punto fijo y 𝑏, +∞ ⊂𝐵 𝐴 ;
Si 𝛽≤1, entonces 𝑓 − no posee un punto fijo y −∞, −𝑎 ⊂𝐵 𝐴 ;
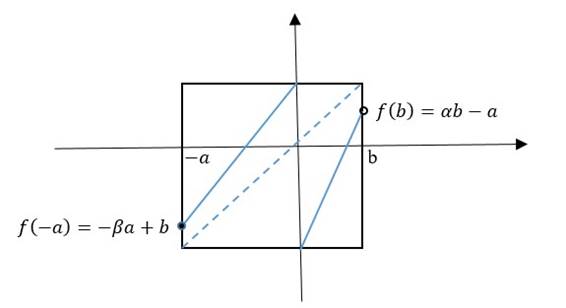
Corolario 3.8 Suponga que 𝑓 satisface la condición 1. El conjunto 𝐴 es atractor global para 𝑓 sí, y solo si, 𝛼= 𝛽=1. Ver figura 3.
Demostración. (⇒) Suponga que 𝐴 es un atractor global, esto implica que 𝑓 no tiene puntos fijos. Por tanto por lema 3.5, 𝛼≤1 y 𝛽≤1. Si 𝛼<1 por observación 3.4, 𝛽>1 y esto es una contradicción. Así, 𝛼=1. Ahora, si 𝛽<1 por observación 3.4, 𝛼>1 esto es una contradicción, luego 𝛽=1.
Proposición 3.9 (Reciproco del Teorema 3.5) Suponga que 𝑓 satisface la condición 1. Si 𝐴 es un atractor entonces, 𝑓 satisface la condición 2.
Demostración. Suponga que 𝑓 no satisface la condición 2. Por tanto, 𝑓 −𝑎 ≤ −𝑎 y 𝑓 𝑏 ≥ 𝑏. Si 𝑓 −𝑎 =−𝑎 y 𝑓 𝑏 =𝑏 entonces, 𝛼>1 y 𝛽>1. Por el lema 3.5, 𝑓 𝑛 𝑥 →−∞, 𝑛→+∞, para todo 𝑥<−𝑎 y 𝑓 𝑛 𝑥 →+∞, 𝑛→+∞ para todo 𝑥>𝑝. Esto implica que 𝐴 no satisface la definición 3.1 de atractor. Esto es una contradicción. Si 𝑓 −𝑎 <−𝑎 o 𝑓 𝑏 >𝑏 entonces, 𝑓 𝐴 ≠𝐴, lo que contradice el hecho que 𝐴 es atractor.
Dinámica y Medidas invariantes del Atractor
Si 𝑓 satisface la condición 1 y 2, el teorema 3.6 indica que el estudio de la dinámica de 𝑓 se debe centrar en el estudio de la dinámica del atractor 𝐴. En el caso en que 𝑓 𝑏 =𝑏 se toma 𝐴 como atractor. Parte del estudio de la dinámica de una transformación consiste en describir el comportamiento asintótico de la órbita (el conjunto 𝒪 + 𝑥,𝑓 ={𝑥, ?? 2 𝑥 , 𝑓 3 𝑥 , …, }) de cada 𝑥∈ℝ, como por ejemplo, el conjunto omega-límite 𝜔 𝑥,𝑓 ={𝑦∈ ℝ :existe 𝑛 𝑘 → +∞ con 𝑓 𝑛 𝑘 𝑥 →𝑦} de un punto 𝑥∈ℝ.
En esta sección se mostrará los diferentes valores del parámetro donde la dinámica del atractor de 𝑓 exhibe un comportamiento no trivial, es decir, 𝑓 𝐴 es transitivo o 𝑓 𝐴 admite una medida absolutamente continua a la medida de Lebesgue. Primero comenzamos con la descripción de la dinámica cuando ?? 𝐴 es biyectiva e indicando los valores del parámetro donde esto sucede.
Teorema 3.10 Suponga que 𝑓 satisface la condición 1 y que 𝛼=𝛽=1.
Si 𝑎 𝑏 es racional entonces, existe 𝑛≥2 tal que 𝑓 𝑛 𝑥 =𝑥, ∀𝑥∈𝐴.
Si 𝑎 𝑏 es irracional entonces, 𝜔 𝑥,𝑓 = 𝐴 (clausura de 𝐴) para todo 𝑥∈𝐴, es decir, 𝒪 + (𝑥,𝑓) es denso en 𝐴 .
Demostración. Considere el difeomorfismo ℎ:[−𝑎,𝑏)→[0,1) definida por ℎ 𝑥 = 𝑥+𝑎 𝑎+𝑏 cuya inversa es ℎ −1 𝑥 = 𝑎+𝑏 𝑥−𝑎. Considere la rotación de Poincaré, vista en el intervalo unitario, 𝑅 𝛿 : 0,1 →[0,1) definida por 𝑅 𝛿 𝑥 = 𝑥+𝛿 mod 1, 𝛼∈[0,1), es decir, 𝑅 𝛿 𝑥 = 𝑥+𝛿 𝑠𝑖 𝑥∈[0,1−𝛿) 𝑥+𝛿−1 𝑠𝑖 𝑥∈[1−𝛿,1) .
Sea 𝛿= 𝑏 𝑎+𝑏 y veamos que 𝑓 restricta a 𝐴=[−𝑎,𝑏) es topológicamente conjugada a 𝑅 𝛿 , por medio de la conjugación ℎ. Para ello, se debe probar que ℎ𝑜𝑓 𝑥 = 𝑅 𝛿 𝑜ℎ(𝑥), para todo 𝑥∈𝐴. Si 𝑥≥0 entonces, ℎ 𝑓 𝑥 = 𝑥 𝑎+𝑏 . Si 𝑥<0 entonces, ℎ ?(𝑥) =ℎ 𝑥+𝑏 = 𝑥+𝑎+𝑏 𝑎+𝑏 = 𝑥 𝑎+𝑏 +1. Por otro lado, si 0≤𝑥<𝑏 se tiene que, 1−𝛿≤ℎ(𝑥)<1, por tanto
Si −𝑎≤𝑥<0 entonces, 0≤ℎ 𝑥 <1−𝛿 y
Se ha demostrado efectivamente que 𝑓 ?? :𝐴→𝐴 es topológicamente conjugado a 𝑅 ∝ . Si 𝑎 𝑏 es racional, implica que 𝛿= 𝑏 𝑎+𝑏 es racional por la conjugación topológica se obtiene ítem a). Si 𝑎 𝑏 es irracional, se tiene que
Cuando una transformación es ergódica bajo alguna medida que ella preserva existe una relación con su comportamiento dinámico. Antes de mostrar la existencia de medidas invariantes es necesario que se comience con algunos conceptos de Teoría Ergódica, necesarios para comprender los resultados obtenidos, para ello consideremos (𝑀,𝜇) un espacio de medida sobre los borelianos ℬ del espacio topológico 𝑀.
Definición 3.11 Una función medible 𝑓:𝑀→𝑀 preserva una medida 𝜇 si 𝜇 𝑓 −1 𝐵 =𝜇(𝐵), para todo conjunto 𝐵∈ℬ.
Definición 3.12 Una función medible 𝑓:𝑀→𝑀que preserva una medida 𝜇 es ergódica si para todo conjunto 𝐵∈ℬ con 𝑓 𝐵 ⊂𝐵 se tiene que 𝜇 𝐵 =0 o 𝜇 𝑀\𝐵 =0.
Teorema 3.13 Suponga que 𝑓 satisface la condición 1, 𝑓 −𝑎 =𝑓(𝑏) y 𝛼≠𝛽.
Si log 𝛽 log 𝛼 es irracional entonces, 𝑓 𝐴 admite una medida invariante únicamente ergódica equivalente a la medida de Lebesgue.
Si log 𝛽 log 𝛼 es racional entonces, todos los puntos 𝑥∈𝐴 son periódicos del mismo periodo para 𝑓 𝐴 .
Demostración. Considere la función del intervalo unitario 𝑔: 0,1 →[0,1) definida por:
Donde 0<𝑠<1 y 0<𝑟<1. En el trabajo de (Coelho et al., 1995) se prueba que el número de rotación de 𝑔 es 𝜌= 𝑙𝑜𝑔 𝑟 1−𝑠 𝑙𝑜𝑔 𝑟𝑠 (1−𝑠)(1−𝑟) . Además, prueban que si 𝜌 es irracional entonces, 𝑔 admite una medida invariante ergódica equivalente a la de Lebesgue. Para usar este resultado se probará que 𝑓 𝐴 es topológicamente conjugada a 𝑔, por medio de un difeomorfismo ℎ: −𝑎, 𝑏 →[0,1) de clase 𝐶 ∞ definido por ℎ 𝑥 = 𝑥+𝑎 𝑎+𝑏 donde, ℎ −1 𝑥 = 𝑎+𝑏 𝑥−𝑎, 𝑠= 𝑎 𝑎+𝑏 y 𝑟= 𝛼𝑏 𝑎+𝑏 . Note que, del hecho 𝑓 −𝑎 =𝑓(𝑏), el valor de 𝑟 así tomado satisface que 0<𝑟<1. Para probar que 𝑔∘ℎ 𝑥 =ℎ∘𝑓(𝑥) para todo 𝑥∈[−𝑎,𝑏), primero considere 0≤𝑥<𝑏 entonces, 𝑠= 𝑎 𝑎+𝑏 ≤ℎ(𝑥)<1. Por tanto
Por otro lado,
Al sustituir los valores de 𝑟= 𝛼𝑏 𝑎+𝑏 y 1−𝛼= 𝑏 𝑎+𝑏 se sigue que
Así, 𝑔∘ℎ 𝑥 =ℎ∘𝑓(𝑥). Ahora, si −𝑎≤𝑥<0 entonces, 0≤ℎ 𝑥 < 𝑎 𝑎+𝑏 =𝑠.
Por otro lado,
Al usar el hecho que 𝑓 −𝑎 =𝑓(𝑏) y sustituir el valor de 𝑟= 𝛼𝑏 𝑎+𝑏 se sigue que,
Esto muestra que 𝑔∘ℎ 𝑥 =ℎ∘𝑓(𝑥) para todo 𝑥∈[−𝑎,𝑏).
Ahora, se observa que log 𝛽 log 𝛼 es irracional sí, y solo si, log 𝛽 log 𝛼 𝛽 es irracional. También note que, 𝑟 1−𝑠 =𝛽 y 𝑟𝑠 (1−𝑠)(1−𝑟) = 𝛼 𝛽 . Por tanto, si log 𝛽 log 𝛼 es irracional entonces ??= log 𝑟 1−𝑠 log 𝑟𝑠 (1−𝑠)(1−𝑟) es irracional. Así, 𝑔 con los valores en los parámetros 𝑠= 𝑎 𝑎+𝑏 y 𝑟= 𝛼𝑏 𝑎+𝑏 preserva una medida ergódica equivalente a la medida de Lebesgue. Entonces, por la conjugación que se encontró 𝑓 𝐴 admite una medida ergódica equivalente a la medida de Lebesgue.
Por otro lado, si log 𝛽 log 𝛼 es racional entonces 𝜌= log 𝑟 1−𝑠 log 𝑟𝑠 (1−𝑠)(1−𝑟) es racional y en el trabajo de (Coelho et al., 1995) prueban que existe 𝑛>1 tal que todo punto 𝑥∈[0,1) es periódico de periodo 𝑛 para 𝑔. Por la conjugación todos los punto de [−𝑎, 𝑏) son periódicos de periodo 𝑛 para 𝑓 𝐴 .
Definición 3.14 Una función ℎ:𝐼→𝐼 lineal creciente por partes en un intervalo 𝐼 es uniformente expansora si existe 𝜆>1 tal que ℎ′(𝑥)>𝜆, para todos los puntos donde la derivada está definida. 𝑓 𝐴 es local eventualmente sobre si para cada intervalo 𝐽⊂[−𝑎, 0) o 𝐽⊂(0,𝑏] existe 𝑛≥1 tal que 𝑓 𝐴 𝑛 𝐽 = 𝐴 .
Teorema 3.15 Suponga que 𝑓 satisface la condición 1, si 𝑓 −𝑎 =−𝑎 o 𝑓 𝑏 =𝑏 entonces, 𝑓 𝐴 admite una única medida invariante ergódica equivalente a la medida de Lebesgue.
Demostración. Caso 1. Suponga que 𝑓 −𝑎 =−𝑎 y 𝛼>1.
Note que por hipótesis 𝛽>1. Entonces, 𝑓 𝐴 satisface las hipótesis del Teorema 5.2.1 (Existencia de medidas invariantes) en (Boyarsky & Góra, 1997) por lo tanto, 𝑓 𝐴 admite una única medida invariante absolutamente continua a la de Lebesgue. Del hecho que 𝛽>1 y 𝛼>1, se sigue que, 𝑓 𝐴 es uniformente expansora. Ya que 𝑓 −𝑎 =−𝑎 se tiene que, 𝑓 𝐴 es local eventualmente sobre (o exacta) ver proposición 4 en (Eslami & Góra, 2011).
Caso 2. Suponga que 𝑓 −𝑎 =−𝑎 y 𝛼≤1.
Considere el mismo homeomorfismos usado en el Teorema 3.10, ℎ: −𝑎, 𝑏 →[0,1) definido por ℎ 𝑥 = 𝑥+𝑎 𝑎+𝑏 . Para 𝑝= 𝑎+𝑏 𝑎 y 𝑠=𝛼 se sigue que 𝑓 es topológica mente conjugado a la aplicación lineal por partes
(Barrientos, 2015) prueba que 𝑓 𝑠,𝑝 es eventualmente expansora para 0<𝑠≤1<𝑝, esto implica que 𝑓 𝑠,𝑝 satisface las hipótesis del Teorema 5.2.1 dado en (Boyarsky & Góra, 1997) por lo tanto, 𝑓 𝐴 admite una única medida invariante absolutamente continua a la de Lebesgue.
En ambos casos 𝑓 𝐴 es local eventualmente sobre, esto implica que 𝑓 𝐴 es transitiva ver (Glendinning & Jeffrey, 2019 ). Si 𝑓 𝐴 es transitiva y admite una única medida invariante absolutamente continua a la de Lebesgue, es bien conocido que esta medida es equivalente a la medida de Lebesgue y además ergódica, ver sección 4.3 de (Viana & Oliveira, 2016) y (GÓRA, 2009).
Caso 3. Suponga que 𝑓 𝑏 =𝑏 y 𝛽>1.
Caso 4. Suponga que 𝑓 𝑏 =𝑏 y 𝛽≤1.
Ambos casos son análogos a los casos 1 y 2 respectivamente.
Proposición 3.16 Suponga que 𝑓 satisface la condición 1 y 2, si 𝑓 −𝑎 < 𝑓(𝑏) entonces, 𝑓 𝐴 admite una única medida invariante absolutamente continua a la medida de Lebesgue.
Demostración.
Considere el homeomorfismos usado en el Teorema 3.10, ℎ: −𝑎, 𝑏 →[0,1) definido por ℎ 𝑥 = 𝑥+𝑎 𝑎+𝑏 . Esta función ℎ es una conjugación topológica entre 𝑓 y la aplicación lineal por partes de tres parámetros
para 𝑡= 𝑎 𝑎+𝑏 , 𝑠=𝛼 y 𝑟=𝛽. Por lo tanto, 𝑓 𝑟,𝑠,𝑡 ℎ(𝑥) =ℎ(𝑓 𝑥 ) para todo 𝑥∈𝐴= −𝑎, 𝑏 . En el trabajo de (Ding et al., 2010) se prueba que si 𝑓 𝑟,𝑠,𝑡 0 < 𝑓 𝑟,𝑠,𝑡 1 entonces, 𝑓 𝑟,𝑠,𝑡 admite una única medida invariante absolutamente continua a la medida de Lebesgue. Usando el hecho que 𝑓 −𝑎 < 𝑓(𝑏) se tiene que
Lo que muestra que la 𝑓 𝑟,𝑠,𝑡 conjugada a 𝑓 con los parámetros dados anteriormente admite una única medida invariante absolutamente continua a la de Lebesgue, por lo tanto, por la conjugación 𝑓 admite una medida del mismo tipo.
Discusión
De la demostración del teorema 3.10 se ve que la dinámica del atractor global de 𝑓 para 𝛼=𝛽=1 es equivalente a la famosa dinámica de la rotación del círculo, esto es muy interesante ya que por lo general este tipo de dinámica aparece en variedades diferenciables sin frontera con dimensión mayor o igual a 2 y no en espacios unidimensionales como el caso de la recta real.
El Teorema 3.10 muestra el comportamiento dinámico desde un punto de vista topológico para el caso 𝛼=𝛽=1. En los resultados presentados en el trabajo no se muestra la medida invariante para el atractor global en este caso. Justamente la medida de Lebesgue es la medida invariante en este caso, la cual es la únicamente ergódica, es decir, es la única medida invariante para 𝑓 𝐴 y además es ergódica. La última afirmación se puede ver en (Viana & Oliveira, 2016).
Si 𝑓 satisface la condición 1, note que del hecho que 𝑓 −𝑎 =−𝑎 hace que 𝛽>1 y del hecho que 𝑓 𝑏 =𝑏 hace que 𝛼>1. Si la función satisface una de esas dos condiciones, por la proposición 3.16 𝑓 𝐴 admite una medida invariante ergódica equivalente a la medida de Lebesgue. Conseguir medidas invariantes equivalentes a la medida de Lebesgue por lo general no es fácil, inclusive en el caso uniformente expansor, como por ejemplo en nuestro caso donde 𝛼>1, 𝛽>1, 𝑓 −𝑎 >−𝑎 y 𝑓(𝑏)<𝑏 (ver figura 3). De hecho, (William Parry, 1979) prueba que en el caso simétrico de 𝑓 con 𝛼=𝛽 y 𝑎=𝑏, la medida absolutamente continua a la medida de Lebesgue asociada a la dinámica del atractor 𝑓 𝐴 (que existe por la proposición 3.16) no es equivalente a la medida de Lebesgue sí, y solo si, 1<𝛼< 2 .
Conclusiones
Al observar la existencia del atractor global de 𝑓 para los parámetros 𝛼=𝛽=1 la función ?? no posee puntos fijos. Se puede concluir que para extender el resultado de la existencia de atractor global para funciones no lineales una condición necesaria es que no admita puntos fijos.
La condición 1 (−𝑎≤𝑓(−𝑎)≤𝑓(𝑏)≤𝑏) es necesaria para que el conjunto 𝐴=[−𝑎, 𝑏) sea atractor de 𝑓, pues si 𝑓(−𝑎)>𝑓(𝑏) entonces, 𝑓(𝐴) está propiamente contenido en 𝐴. Por lo tanto, dentro del conjunto 𝐴 hay un conjunto atractor, el cual no fue estudiado en este trabajo.
Si 𝑓 satisface la condición 1, −𝑎<𝑓(−𝑎) y 𝑓(𝑏)<𝑏, del lema 3.7 y el Teorema 3.6 se concluye que, existen dos puntos fijos 𝑞<0 y 𝑝>0 tales que la bacía de atracción del atractor 𝐴 es igual al intervalo [𝑞, 𝑝]. Note que, en este caso 𝑞<−𝑎<0<𝑏<𝑝.
Del hecho que 𝑓 𝐴 sea transitivo implica que el conjunto 𝐴 es un atractor topológico. Si 𝑓 𝐴 no es transitivo no significa que no existe atractor topológico para 𝑓. De hecho, si 𝑓 satisface la condición 1 y 2, 𝛼>1 y 𝛽>1; se tiene que 𝑓 𝐴 satisface las condiciones dadas para la existencia de atractores topológicos probado en (Morales & Pujals, 1997) y ver (Choi, 2004) para la estructura del conjunto de puntos periódicos del atractor topológico. De estos dos trabajos aplicados a 𝑓 𝐴 concluimos que:
Teorema 5.1. Suponga que 𝑓 satisface la condición 1 y 2, 𝛼>1 y 𝛽>1. Si 𝑓 𝐴 no es transitivo entonces existe un conjunto compacto Λ 𝑓 ⊂𝐴 talque Λ 𝑓 es un atractor topológico para 𝑓 y además, el conjunto de puntos periódicos de ?? es denso en Λ 𝑓 .
Si a las hipótesis del proposición 3.16 se le agrega la condición 2 esto implica que 𝐴 es un atractor topológico. Del ítem 3 del capítulo 5 de Discusión, se concluye: para 𝑓 con 𝛼=𝛽 y 𝑎=𝑏, el conjunto 𝐴 es atractor topológico sí, y solo si, 𝛼≥ 2 .
Contribución de Autores
En concordancia con la taxonomía establecida internacionalmente para la asignación de créditos a autores de artículos científicos (https://casrai.org/credit/). Los autores declaran sus contribuciones en la siguiente matriz:
Iñiguez, A.
Ruiz, B.
Conceptualización
Análisis Formal
Investigación
Metodología
Recursos
Validación
Redacción - revisión y edición