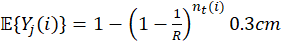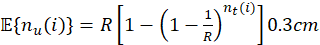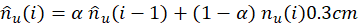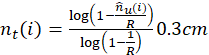1 Introduction
Internet of Things (IoT) is one of the most transformative and disruptive technologies of the upcoming wireless systems that has the potential to change the world radically. It is predicted that billions of heterogeneous IoT devices use cellular connections by 2022 (Ericsson, 2017), which empowers individuals and industries to achieve their full potential. Machine type communication (MTC) is becoming the dominant communication paradigm for a wide range of emerging IoT applications including health-care, smart cities, smart grids, smart transportation, and environmental monitoring. In these applications, a vast number of devices are deployed in a specific area to provide ubiquitous services with minimal (or without) human intervention. Thus, the network has to face an increased load and surges of MTC traffic.
The 5th generation (5G) cellular networks will support this huge number of devices generating sporadic small packets at random times. In this context, the random access channel (RACH) is used to start the communication sessions, aimed at delivering this kind of traffic. The RACH is accessed through a four-message handshake contention-based procedure. First, the devices (named UEs hereafter) wait to the next random access opportunity (RAO) and sends a Msg1 using a randomly chosen preamble from a pool of preambles. Msg1 is detected at the eNB if the preamble is chosen by just one UE in the current RAO; if not, a collision occurs. For each detected preamble, the eNB sends a random access response (RAR) message, Msg2, which includes one uplink grant, from a few grants available. Msg2 is used to assign time-frequency resources to the UEs for the transmission of the connection request. UEs that received an uplink grant send their connection request message, Msg3, using the resources specified by the eNB. Finally, the eNB responds to each Msg3 transmission with a contention resolution message, Msg4. The interested reader is referred to (Tello-Oquendo et al., 2018; 3GPP, 2017b; 3GPP, 2017d; 3GPP, 2017a) for further details.
A fundamental issue is the efficient management of network resources in overload situations; they are produced when many MTC devices react to the same event generating mass concurrent data and signaling transmission. As result network congestion is engendered including both radio access network congestion and signaling network congestion as defined in 3GPP (2017f). This may cause intolerable delays, packet loss or even service unavailability.
The 3GPP proposes the extended access barring (EAB) as one mechanism to guarantee network availability and help network to meet performance requirements under such MTC load (3GPP, 2017e). EAB selectively restricts the UEs’ access attempts to the RACH. Each UE configured for EAB is allocated an access class (AC) in the range 0-9. When the network determines that it is appropriate to apply EAB (using a congestion coefficient), it barres all UEs except one in a given set of ACs, and broadcasts a system information block type 14 (SIB14) containing a 10-bit barring bitmap. The barring is of simple on/off type, where access to each AC is either allowed or not. EAB may be effective whenever the congestion occurs sparingly and during short periods of time (in the order of several seconds). This fact goes in line with the bursty traffic behavior of MTC described in 3GPP (2011).
In the literature, several studies address the EAB mechanism. Some of them misinterpret the EAB behavior or do not conform to 3GPP specifications (Kim et al., 2017; Hwang et al., 2016). On the other hand, studies such as Phuyal et al. (2012), Larmo & Susitaival (2012), Cheng et al. (2015), Toor & Jin (2017) analyze EAB mainly in terms of access success probability and access delay. In such studies, a practical way to implement the congestion coefficient remains unclear since the number of preamble transmissions is not known at the eNB.
In this paper, a realistic method to implement the congestion coefficient is proposed for the proper functioning of EAB. Then, a thorough performance analysis of this mechanism is conducted and the impact of the paging timing on the EAB performance is evaluated. The main contributions of this study are summarized as follows:
The EAB scheme is implemented and evaluated in massive MTC scenarios following the 3GPP directives for this kind of studies.
A method to estimate the congestion coefficient from the number of used preambles at every RAO is proposed, this number of used preambles is effectively known at the eNB so that our proposed solution conforms to the network specifications (3GPP, 2017b; 3GPP, 2017d; 3GPP, 2014; 3GPP, 2017e) and can be successfully integrated into the system.
The impact of the paging timing on the EAB performance is evaluated. For doing so, a realistic situation is considered in which the congestion coefficient is estimated as mentioned above.
The rest of the paper is organized as follows. Section 2 presents the EAB operation mode; then, a method to compute the congestion coefficient used by the network to turn on or off this mechanism is proposed. Section 3 analyzes in-depth the performance of EAB in terms of network key performance indicators (KPIs) and evaluate the impact of the paging timing. Finally, Section 4 draws the conclusions.
2 Extended Access Barring Mechanism
In the following, the operation mode of EAB is presented. Then, a method to implement the EAB congestion coefficient es proposed for its proper functioning.
2.1 EAB operation mode
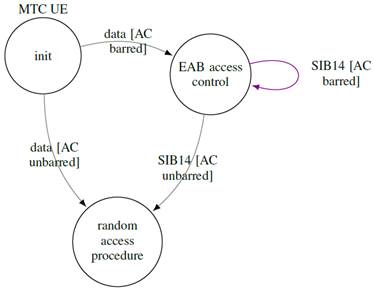
EAB is activated when congestion is detected. For this purpose, the 3GPP defines a congestion coefficient (C 𝐶 𝑊 ) for a moving time-window of 𝑊 ms, as detailed in Section 2.2. With a periodicity given by a modification period parameter, 𝐶 𝐶 𝑊 s are used to update the EAB state. If 𝐶 𝐶 𝑊1 for 𝑊1=1000 ms exceeds 0.4, EAB is turned on and all ACs except one are barred. From here, every time that 𝐶 𝐶 𝑊2 for 𝑊2=500 ms is under 0.4, barring state is released for one AC. The release of ACs proceeds in cyclic order until all ACs are unbarred. Then, if 𝐶 𝐶 𝑊1 is under 0.2, EAB is turned off. Fig. 1 illustrate the state diagram of the operation mode of EAB.
The SIB14 contains the bitmap of barred ACs; the eNB broadcasts messages containing SIB14s with a periodicity of 𝑇 SIB14 ∈{80,160,320,640,1 280,2 560,5120} ms (3GPP, 2017e). Every time the bitmap has to be changed, the eNB notifies it to the UEs through a system information change parameter contained in the paging messages (3GPP, 2017g). Paging messages are sent at specific radio frames and subframes, namely paging frames (𝑃𝐹)s and paging occasions (𝑃𝑂)s, within a paging cycle ( 𝑇 𝑃 ). UEs in idle state wake up at their respective 𝑃𝑂 and read the paging message. UEs calculate their 𝑃𝑂s from their local identifiers, in order that the 𝑃𝑂s of the different UEs are distributed homogeneously throughout 𝑇 𝑃 (3GPP, 2017g). When a UE reads a paging message with system information change set to on, it reads the next message containing the SIB14. To make sure that all UEs are notified of all changes and have a chance to update their EAB information, the modification period is set to the maximum of 𝑇 𝑃 and 𝑇 SIB14 , and changes on the bitmap are notified when they are produced but the SIB14 update is delayed up to the next modification period. When a UE has to access to the RACH, it checks its barring state from the bitmap contained in the latest updated SIB14 as illustrated in Fig. 2.
2.2 Computing the congestion coefficient
The 𝐶 𝐶 𝑊 is defined as WG2 (2012)
where nRAR 𝑊 is the number of RARs sent during 𝑊 ms and nPT 𝑊 is the number of preamble transmissions during 𝑊 ms. To calculate 𝐶 𝐶 𝑊 and therefore update its value at every RAO, the eNB would need to know the number of preamble transmissions at each RAO. But in the commonly assumed collision model defined by the 3GPP, this number is unknown, because those preambles transmitted by more than one UE are not decoded. Therefore, the value of 𝑛𝑃 𝑇 𝑊 defined in (1) should be estimated from the number of preambles used (by at least one UE) at each RAO. This estimation was obtained as follows.
Let 𝑌 𝑗 (𝑖)∈{0,1} be the random variable that denotes the transmission of preamble 𝑗 at RAO(𝑖) given that the total number of preamble transmissions at RAO(𝑖) is 𝑛 𝑡 (𝑖). Then, 𝑌 𝑗 (𝑖)=0 when the preamble 𝑗 has not been transmitted by any UE at RAO(𝑖), and 𝑌 𝑗 (𝑖)=1 otherwise. Its probabilities are
where 𝑅 is the number of available preambles, and
Then, the number of used preambles at RAO(??), 𝑛 𝑢 (𝑖), is
and its expected value is
Since 𝑛 𝑢 (𝑖) is known at the eNB, and assuming that 𝔼{ 𝑛 𝑢 (𝑖)} changes slowly, it can be estimated from a short term time average of 𝑛 𝑢 (𝑖). Let 𝑛 𝑢 (𝑖) be an estimate of 𝔼{ 𝑛 𝑢 (𝑖)} at RAO(𝑖) obtained by exponential smoothing of 𝑛 𝑢 (𝑖),
with 𝛼<1. Finally, from Eq. (5), the estimated value of the number of transmitted preambles used to calculate 𝐶 𝐶 𝑊 is
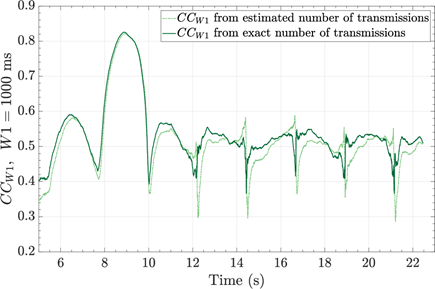
)(1),(2), (3), (4), (5), (6), (7) Several simulations were conducted to check that the values of 𝐶 𝐶 𝑊 obtained using this estimator are very close to those obtained using the real number of preambles transmitted. Fig. 3 illustrates an example of the values of 𝐶 𝐶 𝑊1 for 𝑊1=1000 ms during a congestion episode induced by the MTC traffic benchmark described in Section 3 with 𝑁 𝑀 =30 000 MTC UEs arrivals and ( 𝑇 𝑃 , 𝑇 SIB14 )=(2560,320) ms. The 𝐶 𝐶 𝑊1 obtained from the estimated number of transmissions is compared with the obtained from the exact value of transmissions. As can be seen, the error in the estimated 𝐶 𝐶 𝑊1 is minimal and can be used as real-time congestion coefficient.
3 Performance Analysis
A single cell environment is assumed in which the access requests of MTC UEs follow a 𝐵𝑒𝑡𝑎(3,4) distribution over a period of 10 s, according to the traffic model 2 specified by the 3GPP in 3GPP (2011). This traffic model can be seen as an extreme scenario in which a vast number of MTC UE arrivals (ranging from 𝑁 𝑀 =5 000 to 𝑁 𝑀 =30 000) occur in a highly synchronized manner (e.g., after an alarm that activates them).
Three network KPIs were measured, namely the probability to successfully complete the random access procedure, 𝑃 𝑠 ; the mean number of preamble transmissions needed by the UEs to successfully complete the random access procedure, 𝐾; and the access delay (mean and percentiles) of the successful accesses, 𝐷. These KPIs are in conformance to the 3GPP directives (3GPP, 2011) to assess the efficiency of the LTE-A random access procedure with MTC.
To obtain the above KPIs, a discrete-event simulator was developed; it fully reproduces the behavior of UEs, eNB, and RACH during the random access procedure. A typical physical RACH configuration, prach-ConfigIndex 6 (3GPP, 2017c), is assumed where the subframe length is 1 ms and the periodicity of RAOs is 5 ms. 𝑅=54 out of the 64 available preambles are used for the contention-based random access procedure and the maximum number of preamble transmissions of each UE, preambleTransMax, is set to 10. Additional system configuration parameters can be found in table III in Tello-Oquendo et al., (2018).
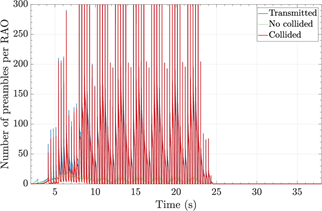
First, an overload situation produced when many MTC devices ( 𝑁 𝑀 =30 000) attempt to access the network is illustrated. Fig. 4 depicts the total preamble transmissions per RAO, preambles with collision (collided), and successful preamble transmissions (no collided); no access control is implemented. It can be seen that when 𝑁 𝑀 =30 000, traffic model 2 leads to network congestion, as the 𝐵𝑒𝑡𝑎(3,4) distribution of UE arrivals exceeds the physical RACH capacity [𝑐(54)=20.05 UE arrivals per RAO as calculated using Eq. (4) in Tello-Oquendo et al. (2018), from the 343rd to the 1 329th RAO. This massive number of UE arrivals results in a congestion period of 𝑇 𝑐 =4.93 s, where up to 300 average preamble transmissions per RAO occur at the 800th RAO. As a result, the average number of successful accesses sharply decreases during this period, and the access success probability is severely affected: 𝑃 𝑠 =31.305 %.
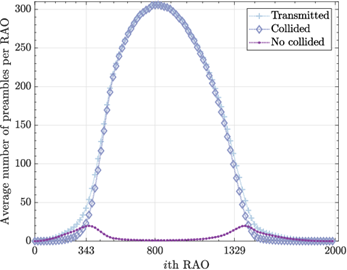
Figure 4: Temporal distribution of preamble transmissions, collided preambles, and successful preambles; traffic model 2, 𝑁 𝑀 =30 000.
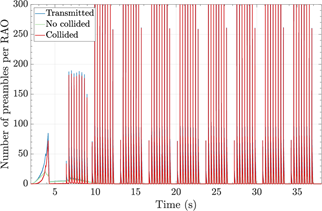
In the following, how the standard EAB mechanism handles congestion episodes as the one described above is shown in detail. Fig. 5, a), b), c) plots the temporal distribution of preamble transmissions when EAB is in operation and ( 𝑇 𝑃 , 𝑇 SIB14 )=({640,1280,2560},320) ms. It can be seen that, when congestion builds up, at 𝑡≈4 s, EAB is enabled. Then, ACs start to be unbarred, one at a time, with a periodicity of modification period = 𝑇 𝑃 . Every time that an AC is unbarred, a number of UEs access the RACH in bursts of periodicity 𝑇 SIB14 =320 ms. Each burst corresponds to those UEs whose 𝑃𝑂s are between two consecutive broadcasts of the SIB14; these UEs access the RACH simultaneously because they update their SIB14 simultaneously. As the 𝑇 𝑃 configuration value increases, the time required to relieve a congestion episode is longer (e.g., the network is able to handle 𝑁 𝑀 =30 000 access requests in ≈37 s with 𝑇 𝑃 =2560 ms, whereas ≈19 s are required with 𝑇 𝑃 =640 ms.)
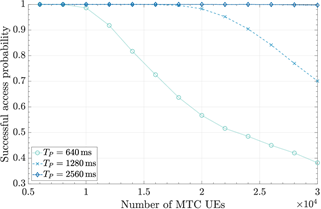
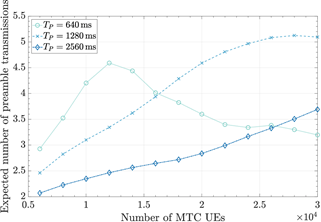
In Fig. 6, a), b), c)the network KPI results are presented for different configurations of 𝑇 𝑃 . Considering feasible parameter values in the LTE-A standard, several configurations for the combination of 𝑇 𝑃 and 𝑇 SIB14 were tested and it was verified that, as in WG2 (2012) and Cheng et al. (2015), combinations in which 𝑇 𝑃 < 𝑇 SIB14 , result in very poor performance in terms of 𝑃 𝑠 . Hence, the results for 𝑇 𝑃 ∈{640,1280,2560} ms and 𝑇 SIB14 =320 ms are shown.

Figure 6: Key performance indicators. (a) Successful access probability. (b) Preamble transmissions. (c) Access Delay.
Fig. 5 shows that 𝑃 ?? increases as the 𝑇 ? duration increases. This is because the greater the 𝑇 𝑃 , the greater the number of information updates per 𝑇 𝑃 , which results in lower intensity of the traffic burst after each SIB14 update. However, the cost of increasing 𝑇 𝑃 is that ACs are unbarred at a slower rate (one AC per 𝑇 𝑃 ), thus increasing 𝐷 as can be seen in Fig. 5. In terms of 𝐾, Fig. 5 illustrates that increasing 𝑇 𝑃 reduces this metric particularly in light-loaded MTC scenarios (i.e., 𝑁 𝑀 <16 000) thus decreasing the energy consumption; however, in heavy-loaded MTC scenarios (i.e., 16 000≤ 𝑁 𝑀 ) this metric increases gradually as 𝑇 𝑃 increases. This is because the delay caused by the paging mechanism: long paging cycle limits the performance of the barring phase. As a result, some devices cannot receive the EAB updated information on time and their accesses will probably fail; therefore, they should start the access attempt again.
To sum up, increasing 𝑇 𝑃 rises 𝑃 𝑠 at the cost of longer access delay while diminishing the number of preamble transmissions in light-loaded MTC scenarios which translates in energy savings for power-constrained MTC devices.
4 Conclusion
In this paper, a practical method to implement the congestion coefficient used by extended access barring (EAB) was proposed. It allows EAB functioning properly for handling congestion in massive machine-type communication (mMTC) scenarios. Through extensive discrete-event simulations, the EAB scheme was analyzed using our proposed congestion coefficient implementation. Then, the impact of the paging timing on the performance of EAB was studied. Numerical results show that a limiting factor of EAB as defined by the 3GPP is that, when a barred AC is released, its UEs initiate their access procedure in bursts of periodicity 𝑇 SIB14 . These bursts cause many preamble collisions during the first RAOs, deteriorating overall performance. On the other hand, increasing the paging cycle rises the successful access probability at the cost of longer access delay while diminishing the number of preamble transmissions in light-loaded MTC scenarios. This results in energy savings useful for the rather power-constrained devices in MTC applications.