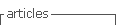INTRODUCCIÓN
Los documentos que norman el Tercer Perfeccionamiento del Sistema Nacional de Educación en la República de Cuba declaran que “
” (MINED, 2021, p. 3). Esta concepción resulta básica para el perfeccionamiento educacional.la política educacional está orientada a formar ciudadanos con una cultura general integral y un pensamiento humanista y creador, que les permita adaptarse a los cambios del contexto y resolver problemas de interés social con una actitud crítica
Los logros alcanzados en la educación promueven la creatividad pedagógica y optimizan el proceso de enseñanza-aprendizaje. La Matemática aporta al cumplimiento de los objetivos del Sistema Educativo cubano en la asimilación de los conocimientos científicos y la formación de una actitud científica hacia los fenómenos de la realidad y de los valores que responden al encargo social de la escuela. Sobre todo, si se tiene en cuenta su carácter integrador y generalizador; así como su incidencia en el desarrollo armónico y multifacético de la personalidad de los estudiantes.
El proceso de enseñanza-aprendizaje de la Matemática se encuentra en renovación, el cambio fundamental radica en que la formulación y solución de problemas se convierte en su eje central, donde la perseverancia de los estudiantes (Gorina & Berenguer, 2017) es básica para el cumplimiento de los objetivos. No obstante, se constatan dificultades en geometría y escaso desarrollo de habilidades en los ejercicios con contenidos geométricos y su aplicación, específicamente en el octavo grado de la Secundaria Básica.
Los estudiantes presentan dificultades en la aplicación de conceptos, proposiciones, procedimientos, propiedades y teoremas en general, objeto de estudio en este grado, manifestándose en la demostración de igualdad de triángulos, donde existen limitaciones en la solución de ejercicios y problemas en los que se aplican los contenidos geométricos. Estas han sido constatadas en la práctica pedagógica, así como en los resultados de comprobaciones y exámenes parciales. Por otra parte, en las orientaciones metodológicas para la Matemática en el octavo grado se aprecian limitaciones en la orientación de cómo dar tratamiento a las demostraciones de igualdad de triángulos.
La habilidad demostrar en Matemática ha sido objeto de estudio por parte de investigadores tales como: Fernández & Gamboa (2018), Lafaid (2018), Iglesias & Ortiz (2019), Bernardis & Moriena (2021), Quero & Ruiz (2021) y Morales et al. (2022), quienes coinciden en el escaso desarrollo que esta habilidad presenta en los estudiantes. Otros como Arnaiz et al. (2020), Llerena (2020) y Ramírez (2021) afirman que no existe una conducción adecuada de los estudiantes para resolver ejercicios de demostraciones geométricas, lo que conduce a la poca motivación y no comprensión de los mismos.
La presente propuesta se dirige a demostrar la factibilidad de aplicación del Programa Heurístico General como alternativa para el tratamiento del contenido de enseñanza en las demostraciones de igualdad de triángulos, en el octavo grado de la Secundaria Básica.
METODOLOGÍA
En este artículo de investigación se presenta una alternativa donde el método general utilizado es el dialéctico materialista que permitió la conjugación de diferentes métodos y técnicas para el estudio (Lorences et al., 2009). En su diseño se tomó como referentes a Hernández et al., 2014, al enmarcarlo en el cuantitativo no experimental, de tipo analítico y transeccional, por las variables que no se manipularon para su estudio y fueron analizadas dentro de un período único.
La investigación se desarrolló con 23 estudiantes de octavo grado de la Secundaria Básica “Juan Marinello” del municipio Ranchuelo, en Villa Clara, Cuba, seleccionados intencionalmente por ser el grupo en que uno de los autores imparte Matemática.
El proceso investigativo se ejecutó en los siguientes pasos, siguiendo la metodología de De Armas & Valle (2011), en cuanto a la consecución de acciones investigativas:
Primer paso: revisión bibliográfica para la determinación de las orientaciones del Ministerio de Educación, acerca de la utilización del Programa Heurístico General en las demostraciones de la igualdad de triángulos.
Segundo paso: se dedicó a obtener el consentimiento de los estudiantes que participarían y la necesaria información acerca de la incorporación del Programa Heurístico General, como alternativa para el tratamiento de las demostraciones de igualdad de triángulos. Obtenido su consentimiento, se aplicó la observación en el proceso de enseñanza-aprendizaje de la Matemática para determinar las carencias que presentan en este contenido de la enseñanza.
Tercer paso: elaboración de la secuencia de acciones teniendo en cuenta las fases del Programa Heurístico General (Ballester et al., 1992) y la propuesta de Arnaiz et al. (2014), como alternativa para el tratamiento de las demostraciones de igualdad de triángulos.
Cuarto paso: ejecución de las acciones y operaciones elaboradas que se incorporaron al proceso de enseñanza-aprendizaje de la Matemática en el octavo grado de la citada Secundaria Básica.
Quinto paso: análisis del producto de la actividad de los estudiantes tanto en sus resultados en clases como en las comprobaciones de conocimientos. El análisis porcentual se usó como procedimiento para la comparación de los resultados.
RESULTADOS Y DISCUSIÓN
La revisión bibliográfica permitió, por una parte, identificar los fundamentos teóricos que sustentan la investigación y por otra determinar las orientaciones del Ministerio de Educación respecto a la utilización del Programa Heurístico General en las demostraciones de la igualdad de triángulos.
En tal sentido, se constató que la línea directriz Geometría en la Secundaria Básica sistematiza los contenidos geométricos adquiridos en el nivel educativo precedente y se introducen nuevos contenidos, en tanto:
. (Ballester, 2018, p. 78)Se profundiza en el tratamiento de los movimientos al estudiar los criterios de igualdad de triángulos, se trata el teorema de las transversales y se introduce la semejanza de figuras, y en particular, la de triángulos. Estos contenidos se aplican a la resolución de ejercicios de cálculo, construcción y demostración
Para octavo grado se plantea formular y resolver ejercicios y problemas intra y extramatemáticos que conduzcan a la estimación, medición y cálculo aproximado de magnitudes geométricas de figuras en el plano y el espacio, aplicando sus propiedades y relaciones. Además, los movimientos del plano, los teoremas estudiados y las razones trigonométricas, para favorecer el análisis y evaluación de las vías más racionales y valorar situaciones relacionadas con la vida cotidiana, otras asignaturas, la ciencia, la técnica y el arte (Álvarez et al., 2014).
En el grado se imparte el tema Geometría plana y cálculo de cuerpos, y en este, el contenido de los teoremas (criterios) de igualdad de triángulos, donde se realizan ejercicios de demostración. Estos criterios son:
si dos triángulos tienen respectivamente iguales dos lados y el ángulo comprendido entre ellos, entonces son iguales (l.a.l);
si dos triángulos tienen respectivamente iguales un lado y los dos ángulos adyacentes a ese lado, entonces son iguales (a.l.a); y
si dos triángulos tienen respectivamente iguales tres lados, entonces son iguales (l.l.l) (MINED, 2014).
Para los autores de este trabajo un ejercicio, según Müller, 1978 (citado por Ballester et al., 1992), es una exigencia para actuar que se caracteriza por: el objetivo de las acciones, su contenido y las condiciones.
Los ejercicios de demostración constituyen problemas debido a su complejidad. La concepción de Campistrous & Rizo (1996) acerca de los problemas es asumida en la investigación, según la cual es toda situación en la que hay un planteamiento inicial y una exigencia que obliga a transformarla. La vía para pasar de la situación o planteamiento inicial a la nueva situación exigida tiene que ser desconocida y la persona debe querer ejecutar la transformación.
El programa de octavo grado (MINED, 2016) declara en sus objetivos que en los criterios de la igualdad de triángulos se realicen ejercicios de demostración aplicando las propiedades de los triángulos, cuadriláteros y circunferencia. Para la resolución de ejercicios y problemas de demostración los procedimientos heurísticos (principios, reglas, estrategias y programas heurísticos, así como medios auxiliares heurísticos) resultan fundamentales para descubrir o encontrar una vía de solución. Además, se conforman como un recurso importante que permite reflexionar sobre su propio aprendizaje y generar nuevos conocimientos.
En la planificación y dirección de los procesos de resolución de problemas se utilizan los llamados programas heurísticos; autores como Polya (1945), Schoenfeld (1989), Ballester et al. (1992), Algarabel et al. (1996) y Quero & Ruiz (2021) han investigado al respecto.
Los firmantes de este trabajo asumen el Programa Heurístico General de Ballester et al. (1992), que consta de fases fundamentales y tareas principales: orientación al problema (comprensión del texto del problema); trabajo en el problema (búsqueda de la idea de solución); solución del problema (ejecución del plan de solución); y evaluación de la solución y de la vía (comprobación de la solución, reflexión sobre los medios aplicados). Este es un programa heurístico aplicable a cualquier tipo de problema, tomándose en su sentido más general.
En 2014, Arnaiz et al. incluyen en el texto: “
” los estudios que realizaron acerca de las habilidades matemáticas, asumiendo que demostrar proposiciones matemáticas es una habilidad matemática generalizada consistente en enmarcar una situación dada en un concepto matemático.La dirección del proceso de enseñanza-aprendizaje de la Matemática para potenciar la integración de los contenidos
Además, constatar que esa situación dada cumple o no con las características esenciales de un concepto. Esto se logra a través de una cadena finita de inferencias lógicas, aplicando conceptos y teoremas estudiados. Afirman que “
” (Arnaiz et al., 2014, p. 31).cuando se utiliza sólo una inferencia lógica estamos en presencia de una fundamentación
Los investigadores proponen cuatro acciones principales, con sus respectivas operaciones para la habilidad demostrar, que se consideraron pertinentes, por lo que se menciona a continuación:
Para la primera acción: reflexionar sobre la proposición dada, declara las siguientes operaciones: identificar el concepto relacionado con lo que se debe demostrar; sustituir los conceptos por sus definiciones; identificar la estructura lógica de la proposición (premisas, tesis); sustituir, si es necesario, la proposición por otra equivalente; y establecer relaciones con otras proposiciones que tengan premisas y tesis similares.
La segunda acción: encontrar la vía de demostración, consta de las siguientes operaciones: reflexionar sobre los procedimientos, estrategias, reglas y medios auxiliares heurísticos; elaborar un plan de demostración (directa, indirecta) donde se precisen las inferencias lógicas necesarias; y reflexionar sobre la vía demostración.
Tercera acción: representación de la demostración, que se materializa en las operaciones: representar por escrito la cadena de inferencias y las fundamentaciones que la hacen comprensible y elaborar una oración que exprese lo que se ha demostrado.
Cuarta y última acción: evaluar críticamente la demostración y consta de: valorar si los pasos dados son suficientes; valorar la cantidad de fundamentaciones indispensables; reflexionar sobre las relaciones lógicas utilizadas; valorar el lenguaje y simbología utilizada; y valorar la posibilidad de utilizar la vía de demostración en otras situaciones.
EL TRABAJO CON PROPOSICIONES MATEMÁTICAS
Al respecto, una proposición matemática es una afirmación que puede ser verdadera o falsa, aunque nunca ambas a la vez, en la que se distinguen dos partes fundamentales: la premisa y la tesis. En el proceso de demostración de proposiciones matemáticas, en este caso ejercicios y problemas de igualdad de triángulos están implícitos los siguientes procesos parciales: búsqueda de proposiciones, proceso en el cual se dirigen las acciones de los estudiantes a establecer una suposición (el teorema buscado); búsqueda de una demostración: proceso en el cual se orienta a los estudiantes a encontrar una idea de demostración para la proposición buscada; y la representación de la demostración: proceso encaminado a la realización de la idea de demostración encontrada (Che, 2007).
Los ejercicios de demostración en que se aplican los teoremas sobre igualdad de triángulos desarrollan la capacidad para demostrar. En todo proceso de demostración el empleo de la heurística contribuye a la sistematización de los contenidos que se aprenden sobre ángulos, cuadriláteros, mediatrices, bisectrices, medianas, triángulos y circunferencia.
Teniendo en cuenta las fases del Programa Heurístico General (Ballester et al., 1992), y la propuesta de acciones y operaciones para la habilidad demostrar de Arnaiz et al. (2014), se elaboró la siguiente propuesta:
Orientación al problema (comprensión del texto del problema), el estudiante debe leer detenidamente el problema; determinar de qué se trata el problema de demostración; formularlo con sus propias palabras y determinar sus palabras claves.
2. Trabajo en el problema (búsqueda de la idea de solución, demostración): identificar el concepto relacionado con lo que se debe demostrar; sustituir los conceptos por sus definiciones; identificar la estructura lógica de la proposición (premisas, tesis); sustituir, si es necesario, la proposición por otra equivalente; establecer relaciones con otras proposiciones que tengan premisas y tesis similares; reflexionar sobre los procedimientos, estrategias, reglas y medios auxiliares heurísticos; elaborar un plan de demostración (directa, indirecta) donde se precisen las inferencias lógicas necesarias; y reflexionar sobre la vía demostración.
3. Solución del problema (ejecución del plan de solución, demostración): el estudiante debe representar por escrito la cadena de inferencias y las fundamentaciones que la hacen comprensible; elaborar una oración que exprese lo que se ha demostrado; realizar cálculos intermedios o demostraciones intermedias en dependencia del criterio seleccionado; escribir la sucesión de inferencias lógicas y sus justificaciones; y concluir la demostración con el teorema aplicado.
4. Evaluación de la solución y de la vía (comprobación de la solución, demostración, reflexión sobre los medios aplicados): debe comprobar en el problema si todas las proposiciones planteadas que llevan hacia la tesis están justificadas; buscar otra vía de solución (utilizar otros criterios); valorar si los pasos dados son suficientes y la cantidad de fundamentaciones indispensables; reflexionar sobre las relaciones lógicas utilizadas; así como, valorar el lenguaje y simbología utilizada y la posibilidad de utilizar la vía de demostración en otras situaciones.
EJEMPLIFICACIÓN
En la 𝐶(𝑂; OC ), (figura 1), AB diámetro, BC = OC , BD tangente a la circunferencia en B. Demuestra que: ∆ACO=∆BCD
Necesaria aclaración de la simbología utilizada:
DEMOSTRACIÓN
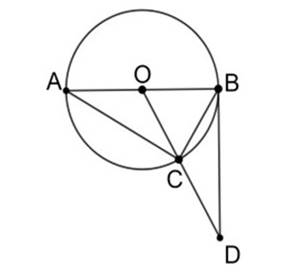
En la Figura 2 de análisis:
En los triángulos ACO y BCD tenemos que: BC = OC por datos.
En la circunferencia C(O; OC ), OC = OA = OB por ser radios.
Luego:
Como OC = OB = BC entonces el ∆OBC es equilátero por tener sus tres lados iguales.
Los ∠γ,∠δ y ∠ε son ángulos interiores del ∆OBC y en todo triángulo equilátero se cumple que tienen igual amplitud o sea ∠γ=∠δ= ∠ε.
El ∠ α es un ángulo seminscrito por estar formado por dos semirrectas de origen común, vértice en la circunferencia, y ser una tangente a la circunferencia y ser la otra secante.
El ∠β es un ángulo inscrito por tener su vértice en la circunferencia y sus dos semirrectas ser secantes.
Entonces:
Tenemos que:
Luego:
Por tanto:
El ∆ACO=∆BCD por tener respectivamente iguales un lado y los dos ángulos adyacentes a este.
Descripción de la actividad del profesor en la fase 1: orienta la lectura detenida del problema y realiza impulsos para su comprensión. Estos impulsos en forma de preguntas deben estar orientados a dirigir la atención a los elementos antes mencionados.
Descripción de la actividad del estudiante en la fase 1: leen detenidamente el problema e individualmente o con ayuda de los impulsos del profesor determinan de qué trata el problema, formulándolo según su vocabulario. Debe tener en cuenta el uso adecuado de la simbología y terminología matemática. En la determinación de las palabras claves es importante que se mencionen aquellos conceptos que aparecen en el texto del problema.
Descripción de la actividad del profesor en la fase 2: dirige mediante impulsos el proceso de análisis de los datos ya sea en el enunciado y en la figura de análisis; así como el de la determinación de las incógnitas les recuerda los criterios de igualdad de triángulos. Aquí entran las posibilidades de los estudiantes para escoger uno de los criterios en dependencia del desarrollo alcanzado y sus conocimientos de geometría.
Impulsos que puede dar el profesor: ¿qué datos ofrece el problema?, ¿qué nos piden?, ¿qué conceptos ofrecen los datos?, ¿qué datos aparecen en la figura de análisis?, ¿es necesario realizar una construcción auxiliar en la figura de análisis?, ¿qué criterios de demostración de igualdad de triángulos se pueden utilizar?, ¿es necesario extraer de la figura los triángulos para tener una mejor idea de la vía de demostración?, ¿con los datos ofrecidos se puede realizar directamente la demostración o hay que realizar cálculo intermedio?, Análisis de las posibles vías de solución a partir de los datos y los criterios.
Descripción de la actividad del estudiante en la fase 2: extraen los datos, individualmente o con ayuda del profesor, analizan las consecuencias directas de las caracterizaciones de los elementos que aparecen en estos. Al hacer el análisis en la figura 2 encuentran vías de solución y realizan cálculos intermedios.
El aseguramiento del nivel de partida en el inicio de la clase les recuerda los teoremas y definiciones relacionadas con triángulos, circunferencia y círculo (rápidamente aparecen el ángulo semi-inscrito y el ángulo inscrito). Al representar la igualdad entre segmentos se percatan de la relación existente entre los radios de la circunferencia. Al tener un par de lados y ángulos iguales, los estudiantes reconocen la vía aplicando el criterio de tener respectivamente iguales un lado y los dos ángulos adyacentes a este.
Al escoger el criterio se reduce el problema a demostrar la igualdad entre dos ángulos que al ser representados en la figura 2 de análisis encuentran la justificación. La representación en la figura 2 de análisis es un elemento fundamental en el proceso de solución del problema.
Descripción de la actividad del profesor en la fase 3: a través de impulsos establece relaciones entre lo que se tiene y lo que se necesita. Además, estos impulsos deben ir comprobando la sucesión de inferencias y sus justificaciones.
Descripción de la actividad del estudiante en la fase 3: con ayuda del profesor analizan las relaciones que aparecen en la figura.
Encontrar la relación entre el par o los pares de elementos que faltan, en dependencia del criterio escogido. Al escribir la sucesión de inferencias se debe prestar especial atención a que no queden afirmaciones sin su correspondiente justificación, llegando a concluir la igualdad entre los triángulos.
Descripción de la actividad del profesor en la fase 4: a través de impulsos comprueba la vía de solución (demostración).
Pregunta: ¿cómo se procedió para buscar la idea de la demostración? Si están todas las proposiciones planteadas justificadas que llevan hacia la demostración de la tesis del problema, ¿qué acciones te resultaron útiles? Busca otras formas de justificar los mismos elementos utilizados en la demostración e indagar si alguien encuentra otra justificación para hallar los elementos de esta vía de solución (demostración). Insiste en buscar nuevas vías de solución utilizando diferentes criterios, orientando su realización en estudio independiente. Sistematiza otros conceptos geométricos y establece relaciones más complejas entre los elementos.
Descripción de la actividad del estudiante en la fase 4: individualmente o con ayuda del profesor comprueba la solución del problema.
Busca la solución por otra vía, siendo encontrado el criterio de dos lados y el ángulo comprendido respectivamente igual. Clasifican los tipos de triángulo y lo utilizan para demostrar las relaciones entre los elementos que necesitan. (La vía menos frecuente fue utilizar el criterio de tres lados respectivamente iguales).
RESULTADOS PARCIALES DE LA APLICACIÓN DE LA PROPUESTA EN LA PRÁCTICA PEDAGÓGICA
Los estudiantes solucionaron problemas con grado de dificultad diferente y como parte de la evaluación parcial se realizó el siguiente ejercicio:
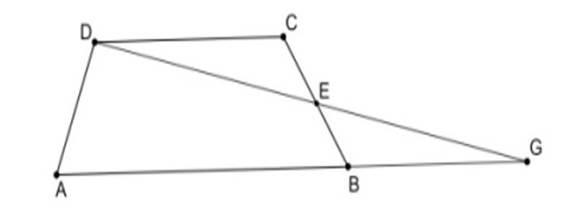
La Figura 3, ABCD es un trapecio de base AB , E es punto medio de BC ; A, B y G son puntos alineados al igual que D, E y G. Probar que CD = BG .
Los resultados del grupo de 23 estudiantes fueron:
El 65,2 % resolvió el ejercicio correctamente, mientras que el 17,3 % demostró incorrectamente la igualdad de triángulos, al determinar un dato con una justificación incorrecta y no concluir; y los demás no fueron capaces de justificar ni señalar los ángulos. 2 estudiantes intentaron hacerlo por un criterio no válido.
El 100 % de los estudiantes identificó los triángulos que tenían que trabajar para realizar la demostración de igualdad de triángulos y dar respuesta a lo pedido en el ejercicio.
Los que resolvieron correctamente utilizaron el criterio (a.l.a), el 59,9 % determinó los lados iguales y los ángulos adyacentes a estos directamente. Los restantes encontraron el otro ángulo y concluyeron la igualdad de los ángulos que necesitaban, para la demostración, por terceros ángulos. El 40,1 % de estudiantes aunque concluyó que los lados son iguales no lo justificó.
Los que no resolvieron el problema en su totalidad (34,8 %) plantearon que:
no poder identificar la relación de los ángulos entre paralelas y lados iguales (55,5 %),
forzaron la demostración por el criterio (l.a.l) al determinar un dato mal justificado (66,6 %) y
utilizaron el criterio (l.l.l), donde no tenían elementos para concluir, presentando dificultades en la fase trabajo en el problema y no llegaron a la conclusión correcta (33,3 %).
Los estudiantes declararon que los criterios (l.a.l) y (l.l.l) no se podían utilizar al no tener medios de justificación entre los elementos de los triángulos, además, sus carencias matemáticas no les permitieron llegar a feliz término.
CONCLUSIONES
Las carencias en cuanto al aprendizaje de la igualdad de triángulos se manifiestan entre los estudiantes del octavo grado en la Secundaria Básica “Juan Marinello”, específicamente al aplicar conceptos, preposiciones y procedimientos en la resolución de ejercicios de demostración.
Los pasos elaborados teniendo en cuenta las fases del Programa Heurístico General y la propuesta de acciones y operaciones para la habilidad demostrar, constituyen una alternativa factible para la impartición del contenido de la enseñanza demostración de la igualdad de triángulos, en el proceso de enseñanza-aprendizaje de la Matemática en el octavo grado de la Secundaria Básica.
Los resultados de su incorporación en la práctica pedagógica son aceptables dada la complejidad del contenido y revelan la necesidad de potenciar propuestas para incorporar el Programa Heurístico General en otros contenidos de la enseñanza de la Matemática