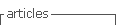Introducción
El arte textil entre los mayas, en las diferentes épocas de su larga historia como pueblo de una avanzada cultura artística, material y científica constituye un hito que define en gran medida su identidad y cultura a lo largo de los tiempos. Es un arte que hace parte de la grandiosidad alcanzada por este pueblo como civilización que hizo grandes aportes a la humanidad y que aún cuenta con sus descendientes directos constituidos, en el caso del estado de Chiapas, por los pueblos hablantes de lenguas mayenses. Son pueblos que practican una de las actividades que junto con la ciencia matemática identificó su cultura originaria: la labor textil.
En este artículo se exponen resultados de una investigación sobre la estética textilera maya y la elaboración de una propuesta didáctica. Durante el primer momento de estudio se revisaron documentos históricos como códices, dinteles, estelas y esculturas del Periodo Clásico Maya, así como crónicas del siglo XVI al XVIII. También se recurrió al testimonio de tejedoras actuales de comunidades de Los Altos de Chiapas usando algunos instrumentos de corte etnográfico para recopilar información.
Esta primera etapa permitió identificar cuatro características fundamentales de la estética contenida en la práctica textil de la zona: la primera hace referencia a que los textiles son un logro expresivo del arte de esta cultura alcanzado gracias a un refinado proceso de pensamiento matemático, el cual parte de una concepción del espacio potencializado a través de un sistema vigesimal. La segunda precisa que la estructura de los tejidos mantiene una lógica procedimental centrada en la espiral, la cual genera secuencias visuales de ascenso y descenso. La tercera define que las figuras del rombo y de la flor de cuatro pétalos que bordan se han mantenido vivas durante más de mil años en la cultura maya como unidades culturales asociadas a sus concepciones matemáticas, artísticas y rituales. La cuarta reconoce la labor del tejido, del brocado y del bordado como un proceso de cálculo, de observación minuciosa del espacio, de manejos de color y producción simbólica compleja propia de la madurez cognitiva de la tejedora.
A partir de estos resultados se realizó una propuesta didáctica que pretende recuperar el pensamiento matemático y la estructura simbólica implícita en la labor textil al trasladarlo a un material interactivo. Se trata de un videojuego estructurado como una dinámica de crecimiento o decrecimiento espacial a través de formas geométricas auto-organizadas -es la misma dinámica que siguen las tejedoras mayas actuales al elaborar y adornar sus telas.
El procedimiento que aquí se describe se presenta como una experiencia particular de investigación artística implementada en un contexto determinado para evidenciar algunas de las estrategias que se pueden seguir para los estudios basados en las artes visuales.
Primeros resultados: estructuras del arte textil maya1
La cultura maya desarrolló un profundo saber astronómico y una extraordinaria precisión en sus cómputos del tiempo. Desde los comienzos del Periodo Clásico (siglos II-X d.C.) los mayas contaban con el concepto del cero y con un sistema vigesimal de numeración en el que las unidades adquirían valor según su posición.2 Estos hallazgos les permitían hacer cálculos muy exactos de momentos alejados en el pasado o el futuro.
El sistema calendárico tan preciso que desarrolló esta civilización mesoamericana se convirtió en estructura para sus textos monumentales de contenido histórico y religioso. El tiempo era visto por los mayas como un espacio habitable en tanto era medible y calculable. Esta consideración sobre el tiempo también permitía que se le asumiera como una realidad espacial por la que transcurrían hombres y dioses.3
El historiador mexicano León Portilla (1968) planteó la existencia de una concepción espacial maya bien definida.4 La describe a través de cuatro grandes sectores cósmicos que convergen en un punto: el centro como quinta dirección del mundo. Junto a los cuatro sectores se encontraban las piedras sagradas, las aves, las semillas, las ceibas cósmicas y los seres correspondientes a cada cuadrante. El monstruo terrestre se presentaba en los cuatro sectores del mundo, cada uno de los cuales tenía su propio color: el rojo en el oeste, el blanco en el norte, el negro en el poniente, el amarillo en el sur y el verde en el centro. En cada sector también crecía la ceiba primigenia con su ave cósmica correspondiente.
En el Códice de Madrid se encuentra una representación semejante a la planteada por Portilla. Allí aparece un árbol cósmico en el centro de dos deidades, cada una de las cuales está tocada por el viento mientras que el árbol se encuentra circundado por los veinte signos de los días. De ella surgen cuatro cuadrantes con huellas de pasos humanos.
Estas concepciones del espacio y el tiempo sentaron las bases para investigaciones posteriores en las que se planteó que la figura del rombo -representación cuatripartita del espacio- usada en los bordados mayas hace referencia a nociones espaciales y temporales de origen prehispánico. Y es que los diseños romboidales han sido los más frecuentes en los trajes esculpidos, tallados, pintados o usados por los mayas desde el Clásico hasta la actualidad.
Como parte de las variaciones de esta dinámica romboidal se encuentra el cuadrado, la greca escalonada con espirales, la flor con cuatro pétalos y la cruz como cruce de un eje vertical con otro horizontal para definir cuadrantes con un centro. En la figura 1 se observa un bordado con estas características. Se trata del decorado de una falda totike actual en la que aparece lo que este pueblo hablante de lengua mayense llama Cruz maya, en ella se representan cuatro sectores a través del cruce de un eje vertical y otro horizontal de cuyo centro emergen dos líneas diagonales que dinámicamente terminan en espirales.

Figura 1 Cruz maya. Bordado sobre falda negra elaborada en telar de cintura. Venustiano Carranza, Chiapas. 2020.
Se ha considerado que el uso de estas formas con cuatro sectores obedezca también a la intención de representar la piel o escamas de algunos reptiles o peces. Así como a la intención de usar el cuadrado o el rombo como referencia a la parcelación de la tierra durante la siembra de la milpa. La investigadora rusa Alla Kolpakova (2018) señala que los diseños romboidales, cuatrifolios o de reja son muy frecuentes principalmente durante el Clásico y el Posclásico tanto para representar la tierra cultivable como la tierra (mundo) cuadrangular. Otros investigadores como Ochiani Kazuyasu (1985) se refieren al uso del rombo como símbolo de la tierra, las direcciones cardinales, el centro, el sol y su órbita diaria.
Como códigos culturales las figuras del rombo, el cuadrado o la flor de cuatro pétalos se han usado como elementos plásticos que permiten que las tejedoras construyan una trama espiralada que se expande o contrae visualmente tal como se observa en la figura 2.
Para bordar las tejedoras usan una estructura matemática centrada en la geometría propia del rombo y la espiral, es decir sus tejidos se estructuran a través de proporciones geométricas continuas de orden cuatripartita.5 Estos patrones autorregulados condensan concepciones espaciales y temporales cíclicas que han hecho parte de la identidad maya desde tiempos remotos.
En la figura 3 se presentan imágenes que muestran detalles de tres casos en los que se usan estas formas arquetípicas continuas: en el primero (A) y el segundo (B) aparecen brocados actuales hechos en telar de cintura con rombos que sintetizan los cuatro sectores expandiéndose a través de espirales; en el tercero (C) se observa un bordado maya del Clásico con los cuatro sectores dispuestos en forma de cruz y un centro definido a través del cruce de dos ejes diagonales con remates en espiral. Esta última se asemeja a la Cruz maya que actualmente tejen para la falda totike presentada en la figura 1.
Aplicación de resultados: enfoque didáctico y tejidos geométricos
Para hacer uso de la lógica constructiva de tipo geométrica de los tejidos mayas en un videojuego se consideró estructurar la propuesta desde un enfoque pedagógico de corte constructivista que propicie el desarrollo del pensamiento matemáticos en niños de la temprana edad.6 A través de este enfoque se promueven acciones educativas para que el niño enfrente problematizaciones que impliquen el uso de relaciones lógicas propias de los conceptos matemáticos.7
Desde esta perspectiva se hace necesario que el niño enfrente un proceso intencional y planeado que le permita acceder al ejercicio de la razonabilidad matemática afectando la totalidad de su pensamiento. Es decir, se trata de que implique diversos aspectos de su historia personal al ubicarlo en un contexto pleno de sentido del que se sienta parte activa. Este es un principio de integralidad en el que el pensamiento se asume como sistema -el que conforma la totalidad del pensamiento.
A partir de estos criterios un videojuego se organiza como material didáctico que ofrece al niño situaciones inteligibles en las que se presenta el problema, las posibles soluciones, las hipótesis, las relaciones o rutas que le demanden razonamientos matemáticos. Todo esto garantiza que la situación movilice su deseo antes que inhibirlo, así el niño se involucrará de forma placentera.8
Debido a que el número es el concepto matemático fundamental con el que se introduce al niño en el ejercicio de la lógica desde su temprana edad, el videojuego se organizó de tal manera que le permita establecer relaciones numéricas con figuras geométricas que se expanden y contraen de forma semejante a como ocurre con las espirales y rombos tejidos en las telas mayas. Contar, adicionar, medir, ordenar, clasificar, establecer relaciones, construir figuras o sustraer parte de ellas son criterios que se usaron para pro gramar las acciones posibles en el videojuego.
Rubén Henao y Mónica Moreno, investigadores de la Universidad de Antioquia, explican que “los procesos que forman parte del pensamiento lógico son: definir, identificar, caracterizar, comparar, clasificar, recodificar, demostrar, describir, explicar, justificar, argumentar y valorar” (Moreno, 2016, p. 96). Exponen además que “es necesario aprender y enseñar a pensar si queremos acceder a un pensamiento más eficaz y mejorar los procesos de razonamiento. […] Por tanto, formar personas que sepan pensar críticamente significa enseñarles a utilizar la lógica para razonar” (p. 96).
Con base en esta perspectiva se usó el concepto de lo numérico como una mediación oportuna y eficaz para movilizar el pensamiento del niño al incitar el uso de relaciones lógicas.9 A partir de esto se implementaron procesos lógicos de tipo geométrico propios del arte textil maya para desarrollar los esquemas mentales necesarios para dotar al niño con instrumentos intelectuales que favorezcan su razonabilidad matemática. Y es que el carácter exponencial de la lógica matemática presente en la labor textil de los mayas incluye un pensamiento en continua apertura en tanto su dinámica visual contiene la noción de infinito -no hay un punto de partida ni uno de cierre definitivo . Es por ello que el pensamiento se expande a partir de una lógica cíclica que reconoce el todo como conexión de partes recíprocas e ilimitadas.
La estructura de auto-semejanza de las figuras geométricas que crecen y decrecen en el espacio como ocurre en los bordados mayas generan una relación continua entre los diversos conjuntos del concepto número. Adentro y afuera, arriba y abajo, atrás y adelante, antes y después, son elementos que convergen en la dinámica del vídeo juego para incitar al niño a que establezca relaciones espaciales ordenando, clasificando, contando, restando o midiendo figuras romboidales y espiraladas.
Se busca generar la posibilidad de que el pensamiento del niño alcance niveles de abstracción que lo involucren en una razonabilidad con la exigencia mental suficiente para darle presencia a su pensamiento de tal manera que pueda argumentar, diferenciar, caracterizar o proponer otros pensamientos. Pensamientos que no sólo se organicen desde la lógica clásica -la de tipo aristotélica que ha dominado en la enseñanza de las matemáticas durante siglos- sino que tenga otras posibilidades de argumentación o demostración.10
Es así que el videojuego le ofrece al niño alternativas de razonabilidad en las que además de deducir o inducir pueda argumentar usando un razonamiento abductivo. También abre la posibilidad para abordar los conceptos matemáticos primarios sobre la base de otras formas de pensamiento diferentes a los de la lógica aristotélica, como es el caso de la lógica maya.
Producto final: el videojuego y su dinámica visual
El videojuego llamado Urdimbre se centra en elementos de diseño y animación que buscan generar relaciones significativas entre el jugador y el producto.11 Los principales elementos de diseño que se usaron para propiciar la interacción se basaron en elementos gráficos y visuales sutiles y pausados para activar un diálogo contemplativo entre el usuario y la aplicación digital. Es decir, se recurrió al uso de colores en tonos vibrantes con líneas suaves desde las que se configuran formas geométricas auto-semejantes. Los ritmos de animación son graduales y tranquilos para propiciar que el jugador se involucre con una actitud atenta y reflexiva.
Se busca que estas características de diseño propicien un pensamiento imaginativo en el niño ya que se considera que esto potencializa la capacidad de abstracción. El juego está programado a través de una narrativa visual en la que el usuario, en este caso el niño, interactúa creando posibles rutas de construcción de espacios que se amplían o reducen. Para ello se le presenta como soporte visual una cuadrícula -semejante a la urdimbre de la tejedora- desde la cual le sea posible la continua construcción geométrica.
Por su parte la programación digital del juego presenta retos como obstáculos o niveles de dificultad con los que se busca promover situaciones para que el jugador se sienta impulsado a establecer relaciones de orden, de clasificación, de equivalencia, de adición o sustracción. Cada uno de los niveles está programado con base en los esquemas mentales que se requieren para favorecer el pensamiento lógico formal del niño de tal manera que pueda establecer comparación de triadas, reconocer la noción de “mediano” o “entre”, organizar a través de semejanzas o establecer relaciones por composición o descomposición cualitativa.
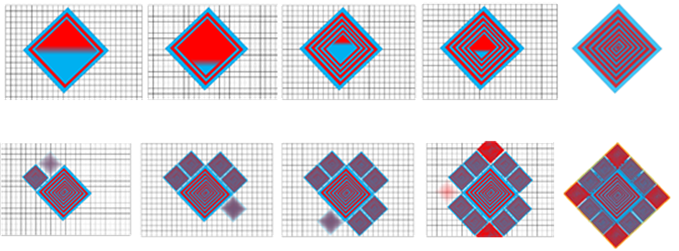
Los niveles de dificultad no ocurren bajo una secuencialidad lineal, sino que lo hacen desde la posibilidad de entrar o salir, subir o bajar, contraer o expandir espacios o figuras de manera simultánea o paralela. En la figura 4 se observan algunas características de la dinámica visual que sigue el vídeo juego.
Estas características usadas en una aplicación multimedia permiten que el niño realice actividades de creación, ensayo y experimentación en ambientes virtuales que lo involucran en procesos de aprendizaje activo para la formación de su pensamiento argumentativo y demostrativo a partir de una perspectiva artística.
Consideraciones finales
El arte a través de colores, figuras, composiciones, diseños, construcciones espaciales, modulaciones o texturas está en posibilidad de abrir procesos cognitivos de un orden contemplativo en los que se construyan nuevos sentidos para abstraer, pensar y proponer estructuras de razonabilidad centradas en estéticas ancestrales.
Se hace necesario que los procesos de investigación artística se sujeten a los contextos mismos de estudio para generar la aplicación de resultados a través de propuestas que recurran a las artes visuales y la transdisciplinariedad como estrategias procedimentales capaces de incidir directamente en dichos contextos.
Es necesario realizar estudios a profundidad sobre la lógica de las producciones textiles de origen prehispánico para identificar con precisión los ejercicios de razonabilidad que las estructuran. Estos estudios podrán ser un aporte hecho desde el arte al análisis de la razonabilidad matemática no occidental, así como del posible uso de estéticas milenarias en procesos educativos actuales.
Se asume que el videojuego Urdimbre favorecerá procesos educativos en los que sea viable acceder a un pensamiento crítico en el que los niños de temprana edad tendrán las bases lógicas de un razonamiento que sienta sus bases en procedimientos de orden artístico.