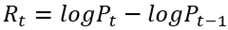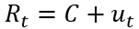1. Introducción

Es un fenómeno notorio que muchas de las series financieras llevan una volatilidad que aparece agrupada, es decir que periodos de bajo riesgo están seguidos por otros de esta misma índole mientras que, al contrario, periodos de turbulencia en los mercados suelen persistir también en el tiempo. Todo ello se puede resumir con la frase de que está presente una heterocedasticidad condicional autorregresiva. La misma puede ser modelizada a nivel econométrico de varias maneras, aquí se escoge en una primera instancia la técnica GARCH como la concibió Tim ^{Bollerslev en 1986}, que no es otra cosa sino una generalización de un modelo ARCH. De hecho, ^{Sharma y Sharma (2015}) demuestran como los modelos tradicionales superan en la capacidad de pronóstico a los modelos más recientes y más sofisticados cuando son aplicados a índices accionarios. Entonces, después de haber verificado que la suma de los parámetros es exactamente igual a 1, se decide volver a estimar el modelo mediante la técnica IGARCH (1,1). La hipótesis fundamental es que los mercados son eficientes por lo que las variaciones diarias del índice ecuatoriano Ecuindex, el cual representa una síntesis de las 10 más grandes empresas cotizadas en la bolsa de valores del país, son fundamentalmente impredecibles (en la metodología esto se traduce en ausencia de predictores retardados para la ecuación de la media).

En segundo lugar, puede sorprender un poco, pero no existe una investigación actualizada de este tipo para Ecuador. Si bien, ciertamente existen modelos GARCH aplicados a ciertas acciones, sobre todo a nivel de tesis de licenciatura, falta un análisis que considere en su profundidad el índice Ecuindex y es por ello que se quiere llenar este vacío de conocimiento. A nivel internacional en cambio son muchos los avances realizados, en particular se puede pensar por ejemplo a los trabajos realizados para el NYSE, en donde es muy común aplicar un GARCH (1,1) como el que se implementa aquí en una primera instancia.

En fin, es necesario comprender la importancia del estudio, el cual mira a entender como se ha comportado la varianza del rendimiento de los activos ecuatorianos como medida fundamental de riesgo financiero para este país: conocer el timing de entrada y salida es muy importante como decisión de inversión para una cartera diversificada. Un inversor adverso al riesgo estaría entonces dispuesto a invertir más favorablemente en periodos de baja volatilidad y la predicción de las varianzas puede hacer posible disponer de intervalos de confianza precisos (^{Stock y Watson, 2012}). En segundo lugar, esta misma información es decisiva para calcular medidas de riesgo que son usadas en los bancos como por ejemplo el VAR. Además, para muchos productos derivados su cotización depende de la fórmula de Black y Scholes en donde es fundamental conocer la volatilidad.

2. Revisión de literatura

La importancia de usar modelos GARCH en econometría es señalada con énfasis por ^{Engle (2001}), el cual nos dice como la varianza debe ser modelizada y no simplemente ser tomada como constante.

Un trabajo reciente y de resumen de los principales modelos existentes hoy en día es realizado por ^{Drachal (2015}), el cual subraya como la mayoría de estos prevén un solo rezago para el error y la varianza y resultan útiles para la estimación.

Un estudio aplicado a los tres más grandes índices bursátiles mundiales es el de ^{Furió y Climent (2012)}, los cuales realizan un modelo GARCH, pero con rendimientos que no siguen una curva normal sino con colas modificadas: según ellos esto resultaría importante para la predicción.

Como se mencionó anteriormente, ^{Stock y Watson (2012}) realizaron este tipo de análisis para el mercado accionario americano del NYSE. Los mismos encontraron significativo y fundado el modelo, en donde se verificó la presencia de una volatilidad agrupada.

Otra importante investigación es realizada por ^{Riasco (2014)}, el cual hace un análisis de riesgo para los tres principales índices bursátiles de EEUU y encuentra que hay un aumento en la varianza condicional después del atentado a las torres gemelas y después de la crisis financiera de 2008 con consecuencias persistentes para uno de estos índices, respectivamente el Dow Jones.

^{Espinosa y Vaca (2016}) son responsables de un importante hallazgo ya que en su trabajo aplicado a la bolsa de valores de Colombia encuentran que para la modelización es recomendable realizar una metodología no solo frecuentista sino también bayesiana que contemple innovaciones t de student y no únicamente normales.

^{Lindberg (2016}), muestra como el modelo GARCH (1,1) es útil para ser implementado tanto para una acción como para un índice y de hecho este autor lo aplica al SP500.

Por lo que se refiere a Ecuador, un trabajo importante es realizado por ^{Tapia y Pamela (2017}), en donde el estudio es realizado para las acciones de la empresa Holcim SA: en este caso también el modelo GARCH es aplicado con éxito, pues se ha demostrado que el mismo resulta ser un modelo eficiente para el análisis de volatilidad de la empresa.

Otro trabajo que merece ser mencionado es el de ^{Bermudez (2014}), el cual consta de tres ensayos inherentes el mercado accionario ecuatoriano y en un capítulo se dedica enteramente a realizar estimaciones GARCH para distintas empresas del país.

3. Materiales y métodos

Parece oportuno empezar esta sección describiendo un poco acerca del problema de investigación y a tal propósito la pregunta en este caso sería: ¿Cómo se presenta la volatilidad de los rendimientos obtenidos a partir de las cotizaciones diarias del índice bursátil Ecuindex en este horizonte temporal de dolarización (años 2004 - 2017)?

Las hipótesis son las siguientes:

En base al primer punto de la lista lo que se supone es que los precios describen el valor fundamental de los activos e incorporan toda la información disponible hasta el momento. Por lo tanto, el futuro tiene un aspecto imprevisible que hace que los operadores financieros en media no pueden batir el mercado. Todo ello implica que la información pasada no sea útil para predecir y esto se traduce en una ecuación para la media que solo involucre una constante y un término de error estocástico.

Por lo que se refiere al segundo punto, debido a la comprobada heterocedasticidad existente en los mercados financieros, no es posible realizar una estimación MCO y es por ello que se desarrollaron los modelos GARCH, los cuales permiten que el riesgo varíe a lo largo del tiempo.

Es interesante considerar ahora la tercera hipótesis, la cual se basa en los hallazgos encontrados por ^{Brooks (2015}) en su famoso libro de econometría financiera: el autor argumenta que en la aplicación de modelos GARCH para los rendimientos es bastante común encontrar un valor igual a uno para la suma de los rezagos del cuadrado del error y de los rezagos de la misma varianza.

En segundo lugar, parece oportuno describir un poco los objetivos. El objetivo general entonces es determinar si la volatilidad se puede explicar mediante un modelo de heterocedasticidad condicional autorregresiva generalizada.

Los objetivos específicos son los siguientes:

Con la finalidad de poder describir el primer objetivo específico es necesario en primer lugar explicar sobre la muestra. Los datos son tomados con cadencia diaria a partir del 5 de enero de 2004 hasta el 31 de marzo de 2017 en donde los precios del índice Ecuindex fueron proporcionados por la bolsa de valores de Quito, véase a tal propósito la figura 1.

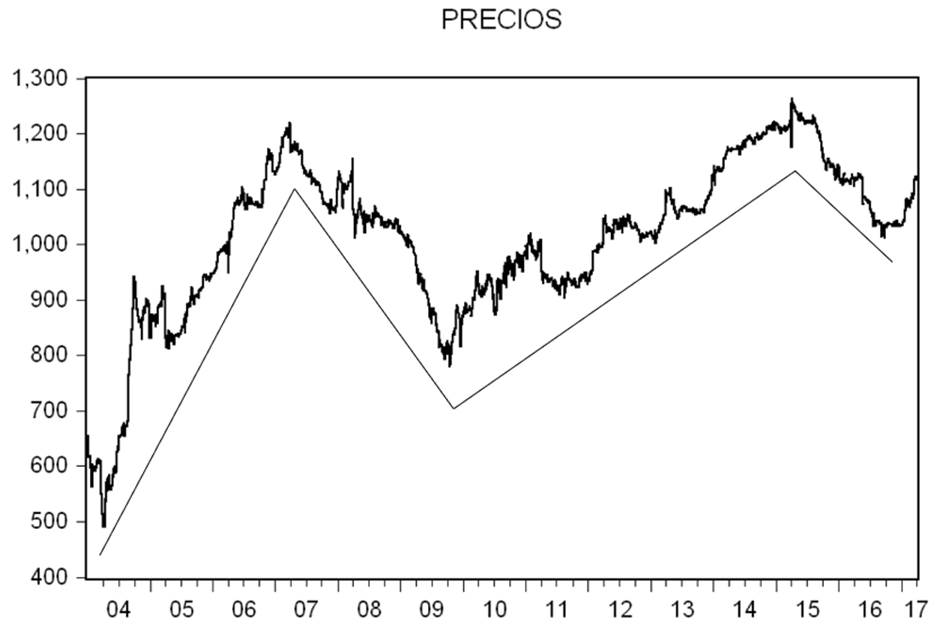
Nota. En el eje de abscisas se encuentra la fecha y en el de ordenadas el valor correspondiente del índice. Las líneas debajo de las cotizaciones representan las tendencias.

Figura 1 Cotizaciones diarias Ecuindex. 

Lo que se puede observar es que la tendencia es al alza hasta principios del 2007, luego parece haber un efecto contagio en el periodo de crisis financiera global por lo que el Ecuindex pierde valor y tarda muchos años para volver a la cotización pre crisis, de hecho, esto ocurre solo a partir del 2015. Después de esa fecha se vuelve a tener una tendencia a la baja que probablemente refleja la crisis que se dio con la falta de liquidez por el excesivo gasto y consecuente endeudamiento del gobierno.

Habiendo llegado hasta este punto, es posible finalmente mostrar cómo se obtuvieron los rendimientos: estos son calculados como la diferencia logarítmica entre los precios de un día a otro. La respectiva fórmula para encontrarlos fue:

(1)

En donde representan los rendimientos, 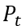los precios al momento t y los precios del día anterior¹

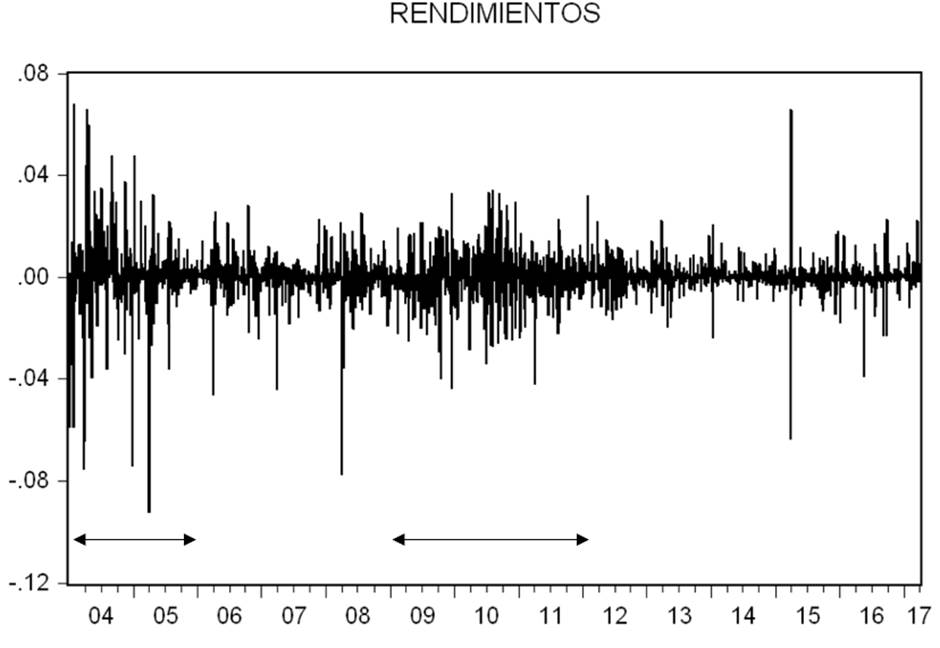
Nota. En el eje de abscisas se encuentra la fecha y en el de ordenadas el valor del rendimiento. Las flechas indican los periodos en donde se agrupa la volatilidad.

Figura 2 Rendimientos del índice. 

Como se puede observar, se registra una alta volatilidad en el primer año, es decir entre 2004 y 2005 y también desde 2009 hasta 2011 como indicado por las flechas. También se puede ver un pico de volatilidad negativa a principios de 2008 y otro pico esta vez simétrico a principios de 2015. Al contrario, la figura muestra que se registra un periodo bastante tranquilo para los años 2012, 2013 y 2014.

En segundo lugar, cabe señalar como en promedio los rendimientos parecen ser aproximadamente 0 y si se excluyen raros casos, por ejemplo, como acontece después de enero 2008 en donde los rendimientos bajan de manera más pronunciada, parecen también ser simétricos, es decir que suben y bajan en igual cuantía. Ello excluye la posibilidad de implementar modelos GARCH asimétricos como por ejemplo los EGARCH o los GJR GARCH entre otros.

El segundo objetivo específico se refiere a la estimación de la volatilidad. A tal propósito es necesario explicar un poco más acerca de las variables que entran en la regresión. En primer lugar, entonces, se tiene la variable dependiente para la ecuación de la media que en este caso está representada por los rendimientos 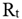mientras que las variables independientes o explicativas están representadas por un término intercepto o constante (C) más una componente estocástica, llamada también término de error u t que en este caso se supone heterocedástico y por lo tanto tiene que ser modelizado más adelante en la ecuación de la varianza. Es importante señalar como esta primera ecuación de regresión es idéntica para ambos modelos GARCH e IGARCH. La ecuación número 2 que representa entonces esta ecuación para la media, no presenta otras variables explicativas adicionales retardadas puesto que se tiene como hipótesis que los mercados financieros son eficientes.

(2)

Es muy importante señalar como 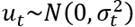es decir que se distribuye normalmente con media igual a 0 y varianza igual a 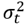. Esta última es muy importante puesto que representa al mismo tiempo la variable dependiente para la ecuación de la varianza que en el caso del primer modelo GARCH (1,1) está expresada con la siguiente fórmula:

(3)

Como se puede observar en la ecuación 3, aquí las variables independientes están constituidas por un término intercepto llamado por un componente representado por el primer retardo del cuadrado del error 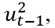llamado también componente ARCH que tiene como respectivo coeficiente el valor de y por un regresor representado por un único rezago de la varianza, 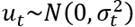el cual tiene su respectivo parámetro 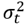. Entonces, un valor para el coeficiente 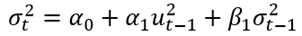pequeño e inferior a 0.05 y un valor al mismo tiempo de grande y superior a 0.85 estaría a indicar un mercado financiero más tranquilo o menos volátil y viceversa si 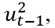resultase de gran amplitud y relativamente pequeño entonces el mercado se caracterizaría como más turbulento.

El segundo modelo, respectivamente el IGARCH, se parece al primero, pero tiene como restricción que 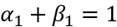y al mismo tiempo no lleva el intercepto 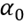. El tercer objetivo específico entonces quiere mostrar como este último modelo tiene sentido y puede representar una identificación inclusive superior respecto al original. De hecho, siguiendo lo que dice la teoría, “en este modelo la varianza es persistente en donde la información presente permanece importante para la predicción de la varianza condicional para todos los horizontes temporales”. (^{Rossi, 2004}, p.13)

La tercera parte que contribuye a definir el problema de investigación está representada por el alcance de la investigación. Este se configura entonces como explicativo puesto que trata de generar un sentido de entendimiento para este tema de riesgo inherente el mercado financiero ecuatoriano. Como se explicó en los apartados anteriores, a tal fin se establecen relaciones causales expresadas principalmente en dos ecuaciones, respectivamente una para la media y otra para la varianza en donde se implementan técnicas econométricas que por su naturaleza implican inferencias estadísticas, es decir tratan de deducir resultados que tienen inmediatas consecuencias descriptivas y normativas.

4. Resultados y discusión

Lo primero que se observa mirando al primer modelo de la tabla 1 es que en la ecuación de la media la constante no resulta significativa y es muy cercana a 0. En la ecuación de la varianza la constante es significativa pero su valor es prácticamente nulo. A todo lo que se acaba de mencionar se considera también el hecho de que la suma de los parámetros 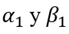es exactamente uno por lo que se justifica ampliamente la decisión de volver a estimar mediante un modelo GARCH integrado (IGARCH), lo cual impone que en la ecuación de la varianza la suma de los parámetros sea uno y por lo tanto excluye también la constante. Mirando entonces a los resultados de esta segunda regresión (modelo 2), se puede afirmar que se obtuvo un valor para el coeficiente 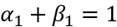relativamente pequeño, cercano a 0.03 y un valor para 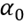relativamente grande e igual a 0.97 por lo que se puede concluir que el mercado financiero ecuatoriano es relativamente estable.

^{Jain y Strobel (2017}) demostraron además como una volatilidad persistente tiene efectos positivos sobre el exceso de rendimiento para portafolios con elevada rotación. Esto parece bastante intuitivo, pues si cada información adicional es determinante para la volatilidad futura entonces es recomendable ajustar la posición de manera frecuente, considerando esto sí oportunamente los límites operacionales y los debidos costes de transacción.

Tabla 1 Resultados de la regresión para la variable dependiente Rendimiento  

Nota. Se usaron las observaciones 2004-01-05:2017-03-31 (T = 3308). Los números entre paréntesis representan los valores z.

*valores débilmente significativos p<0.10; **valores significativos p<0.05; ***valores fuertemente significativos p<0.01

5. Conclusiones

La investigación realizada intentó estudiar el mercado accionario ecuatoriano mediante su índice Ecuindex. El modelo GARCH (1,1) usado al principio nos reveló un orden de integración igual a 1 para la ecuación de la varianza. Es por ello que se implementó después un modelo IGARCH (1,1) que tuvo como resultados un valor para el coeficiente inferior a 0.05. Este valor, que representa el primer retardo del cuadrado del error, puede considerarse bastante pequeño si comparado con otros estudios aplicados. Al mismo tiempo, el coeficiente 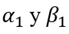, que no es otra cosa sino un retardo de la varianza, resultó ser por consiguiente de grande amplitud y superior a 0.95. Estos hallazgos nos indican que el índice Ecuindex no tiene una grande volatilidad condicional y por lo tanto puede considerarse de bajo riesgo.

En segundo lugar, visto desde otra perspectiva, se puede afirmar que la persistencia de la volatilidad condicional hace que eventos o informaciones relacionadas con la bolsa de valores tengan repercusiones a muy largo plazo (en teoría infinitos). Estudios inherentes este campo sugieren entonces una rotación alta para los portafolios de inversiones. Sin embargo, se recuerda al lector que la presente investigación se realizó sobre un índice, por lo que las conclusiones y recomendaciones que se acabaron de otorgar deben ser tomadas de manera general sobre el conjunto de activos que forman parte del mercado accionario ecuatoriano.