1. Introducción y estado de la cuestión
Una de las competencias que permite a los individuos ser capaces de vincular sus conocimientos matemáticos a las necesidades y exigencias del siglo XXI es la modelización matemática (Maass et al., 2022). En este sentido, se requiere preparar a los profesores con las competencias adecuadas para la modelización y, de este modo, educar a los estudiantes en habilidades para desarrollar este proceso (Blum y Borromeo Ferri, 2009). Si bien en la literatura especializada existe una discusión sobre cómo definir la competencia en modelización (véase Kaiser y Brand, 2015), por una parte, este proceso se considera como uno de los ejes para la resolución de problemas en la evaluación internacional PISA (Organisation for Economic Co-operation and Development, 2019) y, por otra parte, existe un consenso en que el trabajo con modelización trae consigo una serie de beneficios para el aprendizaje matemático (Blum, 2011).
Dado este creciente interés por la modelización a nivel internacional, este estudio pretende aportar una primera visión general sobre una experiencia educativa pionera sobre modelización para profesores de matemática en servicio del sistema escolar panameño. Este programa de formación continua, desarrollado en 2022, reconoce la importancia de integrar la modelización como parte fundamental de la enseñanza de la matemática en Panamá. Es necesario que los profesores incluyan, entre otros procesos relevantes de la actividad matemática, la modelización en sus clases, para lo cual este programa decidió incorporar su enseñanza a los profesores en servicio.
1.1 Modelización matemática
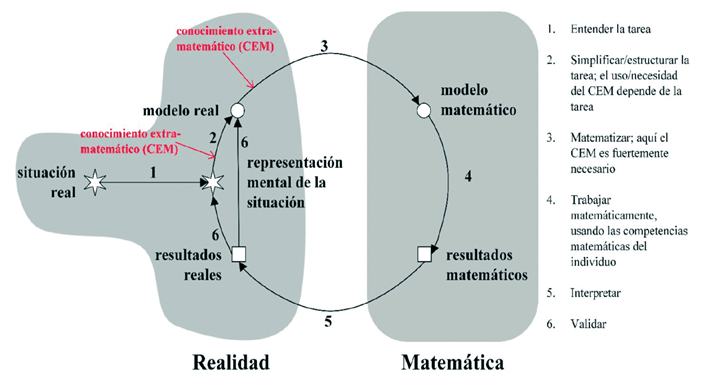
La modelización matemática describe brevemente la traducción de un problema real a la matemática y de sus resultados de vuelta a la realidad (Pollak, 2007). En la literatura especializada se han propuesto diferentes ciclos para analizar el proceso de modelización (Borromeo Ferri, 2006) y han emergido distintas perspectivas sobre su implementación (Preciado et al., 2023). En este estudio se adopta el “ciclo de modelización desde una perspectiva cognitiva” (ver figura 1), propuesto por Borromeo Ferri (2018), el cual se enmarca en la perspectiva realista de trabajo con modelización (Abassian et al., 2020).
La elección de este ciclo para este estudio se justifica por: (a) la experiencia previa de los autores en trabajos teóricos (véase Ledezma et al., 2023) y (b) su uso es parte de la experiencia educativa que se reporta en este artículo. Para explicar el funcionamiento del ciclo de la figura 1 se utiliza como ejemplo el Problema Pan de Azúcar, el cual se presentó durante esta experiencia educativa.
Pan de Azúcar: El teleférico de Pan de Azúcar toma, aproximadamente, tres minutos para su recorrido desde la estación en el valle hasta la cima de la Montaña Pan de Azúcar en Río de Janeiro. Se mueve a una velocidad de 30 km/h y cubre una diferencia de altura de, aproximadamente, 180 metros. El ingeniero jefe, Giuseppe Pelligrini, prefirió mejor caminar, como lo hizo en el pasado, cuando era un montañista. Primero, corrió desde la estación del valle a través de la vasta llanura hacia la montaña, y luego la escaló en 12 minutos. ¿Cuán grande es la distancia, aproximadamente, que Giuseppe tuvo que correr desde la estación del valle hasta el pie de la montaña? (adaptado de Blum y Leiß, 2007, p. 224)
La situación real viene dada por el enunciado del Problema Pan de Azúcar, en forma de un texto con una imagen. Mediante su comprensión, se puede formar una representación mental de la situación, lo que involucra, por ejemplo, establecer relaciones con las vacaciones y los sitios turísticos (conocimiento extra-matemático), a fin de comprender lo que solicita el problema (la distancia entre la estación del valle y el pie de la montaña). Esta representación mental se debe simplificar y estructurar para así obtener un modelo real que represente la situación real planteada; en este caso se puede simplificar la montaña y el cable como segmentos, y el teleférico como un punto, y luego estructurar estas simplificaciones en un dibujo. El modelo matemático toma en consideración los objetos matemáticos que permiten explicar la situación real planteada; en este caso, se puede aplicar el teorema de Pitágoras. A partir del trabajo con este modelo matemático se obtienen resultados matemáticos, los cuales se deben interpretar en el contexto de la situación real para obtener resultados reales; en este caso se obtienen 1,49 kilómetros, aproximadamente. Ahora bien, ¿tiene sentido esta respuesta en el contexto del Problema Pan de Azúcar? Una forma de validar estos resultados reales sería mediante una aplicación de mapas para medir las distancias en la ubicación real del Pan de Azúcar en Brasil.
Nota. Adaptado deBorromeo Ferri (2018, p. 15).
El proceso de modelización no debe ser entendido en términos lineales, sino como un ciclo, ello debido a que tanto el contexto de la situación real como los aspectos matemáticos involucrados en su resolución pueden incidir en el modelo matemático y en el trabajo matemático con el mismo (Blomhøj, 2004; Borromeo Ferri, 2007). El trabajo con modelización en el aula se suele desarrollar en pequeños grupos de estudiantes, a quienes se les plantea una situación-problema que deben matematizar (Doerr e English, 2003; Shahbari y Tabach, 2019). Esta situación-problema, conocida como problema de modelización, debe cumplir con ciertas características (Borromeo Ferri, 2018): debe ser abierta y compleja, cuya resolución no se limite a una respuesta o procedimiento específicos, y donde los estudiantes deban buscar los datos relevantes; también debe ser realista y auténtica, añadiendo elementos tomados del mundo real y presentando una situación coherente con un hecho que ha ocurrido o que pueda ocurrir en la realidad (en términos de Palm, 2007); finalmente, debe ser un problema (en términos de Schoenfeld, 1994) que sea solucionable a través de un ciclo de modelización, lo que implica el desarrollo de todas las fases que componen este ciclo. De la mano de lo anterior, los problemas de modelización tienden a tener diversos caminos para obtener una solución plausible y coherente con el contexto de la situación real planteada (English, 2003; Lesh y Doerr, 2003).
1.2 Modelización matemática en la educación de profesores
Dada la relevancia de este proceso, diversos estudios han abordado la enseñanza de la modelización para profesores, tanto en formación como en servicio.
Una línea se ha enfocado en los conocimientos y competencias de profesores de matemática. En el contexto austríaco, Kuntze et al. (2013) estudian las autopercepciones de profesores sobre su conocimiento del contenido pedagógico (PCK, por su sigla en inglés [Shulman, 1986]) relacionado con la modelización, considerando tanto el PCK necesario para ayudar a sus estudiantes durante el proceso de modelización en el aula, como lo que piensan sobre su propio desarrollo profesional a nivel universitario. Mediante la aplicación de un cuestionario a 38 profesores en formación y a 48 profesores en servicio, los resultados evidenciaron una necesidad de un desarrollo profesional que no solo abarque el PCK sobre modelización, sino también la enseñanza de estrategias para la autoeficacia pedagógica de los profesores al implementar este proceso, por ejemplo, utilizando herramientas tecnológicas. En esta misma línea de investigación, en el contexto alemán, Greefrath et al. (2022) estudian las facetas de las competencias profesionales para la enseñanza de la modelización (véase Blum, 2015), específicamente, aquellas referidas al conocimiento sobre tareas de modelización e intervenciones en el aula. Estos autores reportan los resultados de un seminario de 12 sesiones impartido a tres grupos de futuros profesores de distintas universidades alemanas, en que se evidenció la mejora del PCK sobre modelización de los sujetos participantes. En el contexto español, Ledezma et al. (2022) estudian los conocimientos y creencias sobre modelización de un futuro profesor a partir del análisis de su argumentación. En este estudio, los autores infieren estos conocimientos y creencias utilizando el modelo de Conocimientos y Competencias Didáctico-Matemáticas del Profesor de Matemática (Godino et al., 2017), el cual aplican a la reflexión realizada por el futuro profesor en su trabajo final de máster (véase otros estudios en esta línea en Batista et al., 2022).
En el contexto singapurense, Ng (2013) aborda la problemática sobre los escasos esfuerzos por incorporar tareas de modelización en las escuelas, a pesar de que el currículo nacional introdujo en 2003 este proceso en la enseñanza de la matemática. Para ello, se comparan los resultados de la implementación de dos cursos de modelización para profesores de educación primaria sin experiencia previa con este proceso: uno con 48 profesores en servicio (a partir de un estudio previo [Ng, 2010]) y otro con 57 profesores en formación (el estudio actual [Ng, 2013]). En ambos cursos, los profesores debieron resolver la tarea Juegos Olímpicos de la Juventud (adaptada desde English, 2013). Los resultados evidencian las similitudes y diferencias entre ambos grupos de profesores al resolver la tarea propuesta, sugiriendo un método de trabajo, para el contexto singapurense, que incluya a profesores en formación y en servicio al momento de abordar la enseñanza de la modelización.
En el contexto estadounidense, Manouchehri (2017) reporta los esfuerzos por asistir a un grupo de profesores de matemática en servicio para desarrollar conocimientos sobre modelización y su implementación en el currículo escolar. El contexto de implementación fue un curso de 25 horas de desarrollo profesional, donde 85 profesores trabajaron en tareas de modelización y discutieron sobre su implementación. En este estudio se reportan los resultados de 25 de los profesores y las profesoras que participaron del curso, donde se evidenció un crecimiento en su conocimiento sobre modelización a partir de los desafíos matemáticos (construcción y trabajo con el modelo matemático), pedagógicos (estrategias para desarrollar este proceso en el aula), y epistemológicos (obstáculos durante el proceso de modelización) que debieron enfrentar.
En el caso de este estudio, se reporta una experiencia educativa pionera con profesores de matemática en servicio de Panamá. El sistema educativo escolar de Panamá se forma por los niveles de Educación Básica General (estudiantes de 4-15 años) y Educación Media (estudiantes de 15-18 años). En este contexto, la Universidad de Panamá, en colaboración con otras universidades extranjeras, implementó dos diplomados para profesores en servicio de ambos niveles educativos durante 2022: “Estrategias Didácticas para la Enseñanza de la Matemática” (Diplomado EDEM) para Educación Básica General, y “Educación Matemática Aplicada a la Secundaria” (Diplomado EMAS) para Educación Media. El objetivo de ambos diplomados fue ampliar las habilidades pedagógicas del profesorado de matemática. Esta investigación se centró en el Diplomado EMAS, donde uno de los tópicos abordados fue la modelización matemática.
1.3 Objetivo y pregunta de investigación
El planteamiento de la pregunta de investigación sobre los resultados de esta experiencia educativa pionera desarrollada en el contexto panameño es el siguiente: ¿Cuáles son los procedimientos de resolución a problemas de modelización por parte de los profesores de matemática en servicio que participan del Diplomado EMAS? Para responderla se utilizó el ciclo de modelización representado en la figura 1 para analizar los procedimientos de resolución a tres problemas planteados a los profesores durante un submódulo de este diplomado. Estas resoluciones fueron clasificadas de acuerdo con las fases y transiciones identificadas en sus producciones escritas. Finalmente, se reflexiona sobre estos resultados y sus posibles implicancias para futuras implementaciones de este diplomado en el contexto panameño.
La relevancia de este estudio radica en dos ámbitos. Por una parte, se aborda un tema poco explorado en el contexto panameño como es la educación de profesores de matemática en servicio sobre modelización. Si bien hay diferentes investigaciones sobre educación de profesores de matemática en Panamá realizadas, principalmente, con base en la experiencia del Diplomado EDEM (véase García-Marimón et al., 2021; Morales et al., 2019), estas se centran en el desarrollo de la reflexión docente utilizando el constructo Criterios de Idoneidad Didáctica (Breda y Lima, 2016). A pesar de que los documentos curriculares nacionales de Panamá no incluyen un trabajo sistemático con modelización para la enseñanza de la matemática (véase Ministerio de Educación de Panamá, 2014a, 2014b, 2014c), el Diplomado EMAS sí incluye este proceso como un tema relevante para enseñar, ya que se asumen las tendencias actuales que promueven la inclusión de la modelización en los procesos de enseñanza y aprendizaje matemáticos. Por otra parte, la Universidad de Panamá, responsable de impartir estos diplomados, es considerada como un referente en docencia e investigación a nivel centroamericano (García-Marimón, 2023; Morales-Maure, 2019). Por lo tanto, esta experiencia educativa se puede replicar en otros países de la región debido a las similitudes socioculturales existentes.
2. Metodología
Para este estudio se siguió una metodología de investigación cualitativa desde un paradigma interpretativo (Cohen et al., 2018). En esta sección se describen los aspectos metodológicos.
2.1 Contexto de la investigación
Esta investigación se desarrolló en el contexto del Diplomado EMAS, impartido por la Universidad de Panamá durante el periodo mayo-octubre de 2022, con una duración total de 320 horas. El objetivo de este diplomado es contribuir al desarrollo profesional docente continuo de los profesores de matemática de educación secundaria panameños, que incluye el diseño, la implementación, valoración, y mejora de procesos de enseñanza y aprendizaje matemáticos, con sustento teórico en el constructo Criterios de Idoneidad Didáctica. En el curso 2022 del Diplomado EMAS participaron 113 profesores, provenientes de distintas zonas del país, quienes fueron agrupados en las cuatro salas virtuales de la plataforma en línea diseñada por la Universidad de Panamá a cargo de un profesor formador. Este programa constó de seis módulos impartidos en modalidad híbrida: (a) Introducción a la Educación Matemática; (b, c, d) Didáctica de la Matemática I, II, y III; (e) Contextos social, familiar, y educativo; y (f) Reflexión sobre la propia práctica. Al término de este programa, los profesores participantes recibieron un certificado por el cumplimiento del curso. Los Diplomados EDEM y EMAS son experiencias educativas pioneras en el contexto panameño, las cuales no están solo apoyadas por un proyecto de investigación gubernamental adjudicado por la Universidad de Panamá, sino que también por académicos de universidades extranjeras (especialmente de España e Hispanoamérica).
2.2 Submódulo sobre modelización matemática y análisis a priori de los problemas de modelización
Dentro del módulo “Introducción a la Educación Matemática” se encuentra el submódulo “Modelización matemática”. Debido a la modalidad híbrida del diplomado, los profesores participantes podían acceder a una explicación general en la plataforma virtual sobre qué es la modelización y cuatro problemas de este tipo que debían resolver. El seguimiento de este trabajo remoto lo desarrollaba el profesor formador a cargo de cada sala virtual. Junto con esta explicación, prácticamente al inicio de este submódulo, se impartió una conferencia dirigida a los profesores participantes y formadores del diplomado, donde se amplió la explicación sobre modelización disponible en la plataforma. En esta conferencia (que duró 90 minutos), el expositor (el primer autor) comenzó explicando qué se entiende por modelización matemática, qué caracteriza a este tipo de problemas, qué estrategias de trabajo con este proceso se sugieren seguir en el aula, y cómo se puede analizar la resolución de un problema de modelización (el Problema Pan de Azúcar en la subsección 1.1) utilizando el ciclo de la figura 1. Estos problemas se presentan en la tabla 1, junto con el análisis a priori de cada uno, en términos del ciclo de modelización considerado como referente teórico del estudio.
Si bien estos problemas de modelización se comentaron durante la conferencia, los profesores participantes debían resolverlos de manera autónoma y cargar sus resoluciones y respuestas a la plataforma virtual diseñada para el Diplomado EMAS. Posteriormente, el profesor formador de cada sala virtual realizaba una retroalimentación sobre las resoluciones para los tres problemas.
2.3 Recolección y análisis a posteriori de los problemas de modelización
Dado que el segundo y tercer autor de este artículo son académicos involucrados en el diseño y coordinación de la implementación del Diplomado EMAS, se contó con acceso total a la plataforma virtual donde los profesores participantes cargaron sus resoluciones y respuestas a los tres problemas de modelización aplicados (instrumentos). Para ello, se solicitó a los profesores participantes que registraran, de la forma más ordenada y explícita posible, todos sus procedimientos de resolución y no solo sus respuestas a estos problemas (datos). De este modo, los profesores participantes podían cargar sus producciones escritas a la plataforma virtual del Diplomado EMAS en forma de documentos escaneados o elaborados con algún procesador de texto.
Una vez recolectadas las producciones escritas, estas se rotularon según el grupo al que pertenecían (G1 a G4) con un número para cada una (P01 a P29). Por ejemplo, la producción G2.P07 corresponde al número 7 del grupo 2. De estas producciones recolectadas se deben tener dos consideraciones: (a) de los 113 profesores participantes, 40 de ellos cargaron sus producciones escritas a la plataforma virtual; (b) de estos 40 profesores participantes, no todos resolvieron los tres problemas de modelización planteados. Por lo tanto, el análisis a posteriori de los procedimientos de resolución de los profesores participantes se realizó a partir de las 40 producciones recolectadas y consistió en: primero, identificar las fases del proceso de modelización en los procedimientos de resolución a cada uno de los tres problemas planteados, a partir de los análisis a priori de la tabla 1; segundo, clasificar estas producciones en cuatro categorías que se pudieron establecer a partir de los procedimientos de resolución identificados, con base en las fases del ciclo de la figura 1, las cuales se describen y ejemplifican en la siguiente sección. De este modo, se puede tener una primera mirada general sobre los resultados de esta experiencia educativa pionera en el contexto panameño.
3. Resultados
En esta sección se presentan los resultados del estudio de acuerdo con los cuatro procedimientos de resolución identificados en las producciones de los profesores participantes.
3.1 Procedimiento de resolución 1 (PR1)
El primer procedimiento de resolución identificado corresponde a aquellas producciones donde los profesores participantes no evidenciaron una comprensión completa del enunciado del problema y/o solo aportaron una descripción de cómo podría ser resuelto. Se tienen los siguientes ejemplos del PR1:
d = Diámetro de la paca. La altura de las pilas de heno sería A = 5d. (Problema Pacas de Heno; Producción G1.P22) Se realiza con una fórmula la distancia entre dos puntos d = Raíz cuadrada del primer punto elevado al cuadrado más el cuadrado del segundo [sic]. (Problema Meandros; G3.P23) El barco, para divisar por primera vez el faro, debe encontrarse a una distancia de la base del faro igual a la altura del mismo, para que la línea de visión del observador, al divisar el faro, forme con la horizontal un ángulo de 45º, teniendo en cuenta la curvatura del planeta. (Problema La Luz de Boston; Producción G2.P09)
3.2 Procedimiento de resolución 2 (PR2)
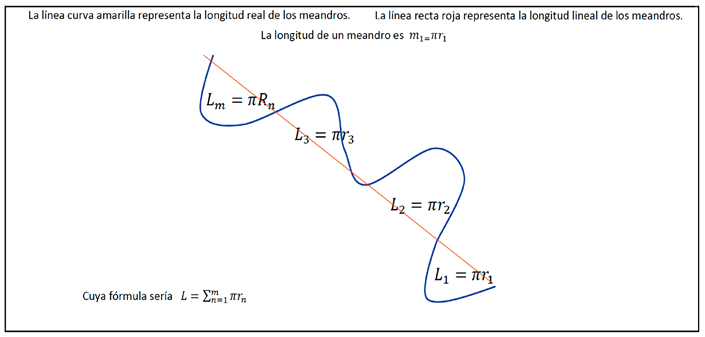
El segundo procedimiento de resolución identificado corresponde a aquellas producciones donde los profesores participantes desarrollaron las fases modelo real → modelo matemático. En estas producciones se consideró como suficiente formular un modelo matemático para resolver el problema, sin siquiera trabajar matemáticamente con el mismo; en otras palabras, se matematizó el problema para darle respuesta. Se tiene el siguiente ejemplo del PR2 para el Problema Meandros en la figura 2:
Nota. Archivo de los autores.
3.3 Procedimiento de resolución 3 (PR3)
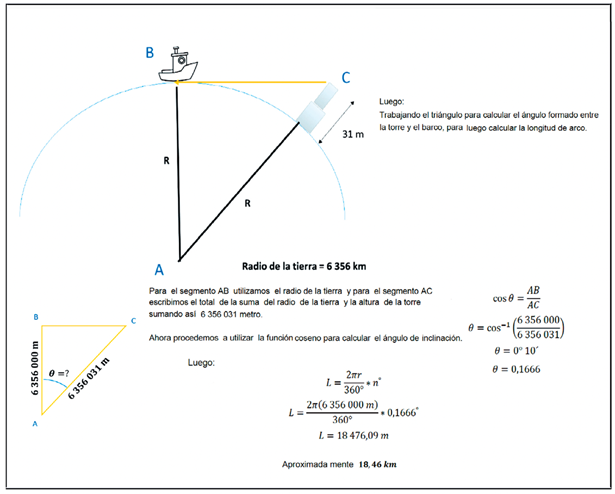
El tercer procedimiento de resolución identificado corresponde a aquellas producciones donde los profesores participantes desarrollaron las fases modelo real → modelo matemático → resultados matemáticos. En estas dos producciones se consideró como suficiente obtener resultados matemáticos a partir del modelo matemático para resolver los problemas, sin necesidad de interpretarlos como resultados reales y, mucho menos, validarlos en el contexto de la situación real planteada; en otras palabras, se trabajó matemáticamente con el problema para darle respuesta. Se tiene el siguiente ejemplo del PR3 para el Problema La Luz de Boston en la figura 3:
Nota. Archivo de los autores.
3.4 Procedimiento de resolución 4 (PR4)
El cuarto procedimiento de resolución identificado corresponde a aquellas producciones donde los profesores participantes desarrollaron un ciclo de modelización completo. En estas producciones se construyó un modelo real de la situación real, se trabajó con un modelo matemático, y los resultados matemáticos se interpretaron como resultados reales en el contexto de la situación real a partir de las consideraciones extra-matemáticas realizadas por el resolutor. Se tiene el siguiente ejemplo del PR4 para el Problema Pacas de Heno en la figura 4:
Nota. Archivo de los autores.
3.5 Síntesis de los resultados
En la tabla 2 se presenta el número de producciones de los profesores participantes según los procedimientos de resolución (PR1 a PR4) que utilizaron para cada uno de los tres problemas de modelización planteados durante el submódulo correspondiente.
4. Discusión y conclusiones
Los resultados de la tabla 2 muestran que la mayoría de los procedimientos de resolución que se pudieron evidenciar en las producciones de los profesores participantes fueron PR1 y PR2. Con respecto a estos resultados, una conclusión plausible que puede explicar esta situación sería que, para el caso del PR1, los profesores participantes no recibieron una formación en modelización más allá de la que se impartió en este diplomado y, para el caso de PR2, que el conocimiento sobre modelización que hayan podido tener se podría interpretar como un intento de matematizar la realidad en vez de desarrollar un ciclo de modelización completo. Como se mencionó al principio, el trabajo con modelización para la enseñanza de la matemática no es parte de los documentos curriculares nacionales de Panamá; por lo tanto, es probable que estos profesores no hayan tenido un conocimiento muy amplio sobre las estrategias de resolución para este tipo de problemas, o experiencias de implementación de la modelización en su práctica educativa.
Los resultados de la tabla 2 también muestran que hubo profesores que evidenciaron el PR3, lo cual se condice con parte de los resultados reportados por Ledezma et al. (2023), en que los futuros profesores de matemática de educación secundaria no se interesaron por volver al “mundo real” para interpretar o validar los resultados obtenidos del modelo matemático utilizado, centrando su atención en las sub-competencias de matematización y trabajo matemático con los problemas propuestos. Además, hubo cinco producciones de los profesores participantes en que se evidenció el desarrollo de un ciclo de modelización completo (PR4), sin embargo, no son un resultado representativo del total de producciones recolectadas.
Estos resultados aportan una primera visión general sobre la enseñanza y el aprendizaje de la modelización en el Diplomado EMAS y para los autores, como académicos involucrados en este contexto, les permite cuestionarse: ¿Qué se debería mejorar/modificar en el submódulo de modelización para futuras implementaciones? Con base en investigaciones previas sobre este tipo de experiencias educativas (véase Borromeo Ferri, 2018; Wess et al., 2021) y en los resultados aquí reportados, se puede concluir que:
Primero, el tiempo dedicado al submódulo de modelización no es suficiente para que los profesores adquieran competencias en modelización por sí mismos y, además, piensen en cómo podrían enseñar/implementar este proceso en su práctica educativa. Dada esta situación, se propone una reformulación que incluya un mínimo de diez sesiones (similar a Greefrath et al., 2022) para abordar la enseñanza de la modelización. Segundo, la conclusión anterior lleva a reformular los aspectos didácticos del submódulo, comenzando desde el conocimiento y competencias previas de los profesores sobre modelización, dividiendo este proceso en conjuntos de fases que forman el ciclo, y luego planteando tareas que trabajen transiciones (o sub-competencias de modelización) específicas (véase Maaß, 2010). Tercero, como etapa final del submódulo, sería interesante que los profesores diseñaran una clase de modelización, incluyendo la resolución y creación de problemas propios, que promueva la reflexión sobre la propia práctica luego de su implementación (véase Ledezma et al., 2022).
La modelización se considera un proceso que enriquece la calidad de la enseñanza y el aprendizaje de la matemática, tal como se evidencia en la experiencia educativa del Diplomado EMAS. Sin embargo, esta experiencia podría tener un impacto aún mayor si se implementan ajustes curriculares en Panamá, los cuales deberían incluir, entre otros aspectos, la integración de la modelización y darle un peso significativo en la enseñanza y el aprendizaje de la matemática en este país. Finalmente, se destaca que este estudio es de carácter seminal en una línea de investigación sobre modelización en el contexto panameño para un mayor desarrollo profesional docente.