1. Introducción
En la literatura, varios autores explican, por medio de diferentes modelos teóricos, qué conocimientos debe poseer el profesorado para desempeñar su profesión (Shulman,1987; Mishra y Koehler, 2006, entre otros). Amaya de Armas et al. (2016) apuntan la importancia de identificar los conocimientos que debe tener un profesor de matemáticas. Para ello, existe el modelo Conocimientos y Competencias Didáctico-Matemáticas del Profesor de Matemáticas (CCDM) de Juan Godino et al. (2017), lo cual es un refinamiento del modelo teórico de Deborah Ball et al. (2008).
Centrándonos en la dimensión didáctica, el profesorado de matemáticas ha de tener, entre otras, la competencia de reflexionar sobre los procesos de instrucción matemática llevados a cabo en la práctica, entre otras razones, porque es una estrategia fundamental para el crecimiento profesional y el enriquecimiento de la docencia. Dentro de la agenda de investigación acerca de la importancia de la reflexión del profesorado sobre su práctica docente, se encuentran la investigación-acción de Elliot et al. (1993), la práctica reflexiva de Schön (1983) y el estudio de lecciones de Hart et al. (2011). Los “Criterios de Idoneidad Didáctica” (CID) que ofrece el marco Enfoque Ontosemiótico del Conocimiento y la Instrucción Matemáticos (EOS) de Godino et al. (2007), es un instrumento diseñado para ordenar y estructurar la reflexión del profesorado articulando diferentes criterios (epistémico, cognitivo, interaccional, mediacional, afectivo, y ecológico) configurándose como uno de los elementos del Conocimiento Didáctico-Matemático (CDM) propuesto por el EOS, denominado conocimiento meta didáctico-matemático (Breda et al., 2017).
Es importante señalar que esta herramienta, CID, ha sido aplicada en diferentes procesos de formación de profesores en diversos países obteniendo resultados satisfactorios en lo referente al desarrollo de la reflexión de los docentes para acrecentar su calidad docente: Ecuador y España (Font et al., 2023), Chile (Seckel y Font, 2020), Costa Rica (Morales-López y Font, 2019), Panamá (Morales-Maure, 2019), Perú (Garcés-Córdova y Font, 2022), entre otros. El “Màster interuniversitari de Formació del Professorat de Secundària de Matemàtiques de Catalunya” atiende al criterio de que los futuros profesores deben realizar prácticas docentes en centros educativos durante su formación inicial y a que, para que perciban la gran complejidad de los procesos de enseñanza y aprendizaje, es necesario reflexionar sobre ellos, siendo la reflexión una herramienta para mejorarlos.
Para conseguir este objetivo, los estudiantes del Máster cursan una asignatura que se denomina Trabajo Final de Máster (TFM) en la que analizan la Unidad Didáctica (UD) elaborada e implementada por ellos mismos en el periodo de prácticas preprofesionales. Para realizar este análisis, los estudiantes utilizan los CID que han estudiado en otra asignatura. Los futuros profesores, basándose en el análisis, rediseñan su UD mejorándola.
Como afirma Font (2011), uno de los temas más importantes en la educación matemática secundaria es el de las funciones. Son nucleares por estar presentes en muchos procesos de modelización, así como por su riqueza y complejidad epistémica.
En este trabajo analizamos, en los TFM sobre funciones de la Educación Secundaria Obligatoria (ESO), la reflexión que los profesores en formación inicial hacen cuando analizan, epistémicamente, la UD que han diseñado.
1.1 Modelo de conocimientos y competencias didáctico-matemáticos (CCDM)
Con la finalidad de mejorar la formación de los docentes de matemáticas, Pino-Fan et al. (2015) proponen un modelo del CDM que explica y determina los conocimientos de un profesor considerando tres dimensiones: matemática, didáctica y meta didáctico-matemática. En esta investigación nos centraremos en la tercera de estas dimensiones.
Para desarrollar esta dimensión meta didáctico-matemática, en el EOS se han propuesto diferentes constructos teóricos, en particular, para la evaluación de procesos de instrucción de las matemáticas, su herramienta esencial es la noción de Idoneidad Didáctica. Se dice que un proceso de enseñanza y aprendizaje tiene un determinado nivel de Idoneidad Didáctica si posee ciertos elementos que posibilitan valorarlo como idóneo, en el sentido de apropiado o óptimo, para que los alumnos transformen los significados institucionales pretendidos o implementados por el docente (enseñanza) en significados personales (aprendizaje), considerando las circunstancias y los medios utilizables (entorno) (Godino et al., 2006a; Godino et al., 2006b). La Idoneidad Didáctica se define a partir de las siguientes dimensiones o CID: IE, evalúa la calidad de las matemáticas que se enseñan; Idoneidad Cognitiva, evalúa, al inicio de la instrucción, los conocimientos previos de los alumnos, y al final, si los estudiantes han aprendido lo que se pretendía; Idoneidad Interaccional, evalúa si las interacciones entre docente-discentes y entre discentes contribuyen al aprendizaje de estos; Idoneidad Mediacional, evalúa la gestión del tiempo y la conveniencia de los materiales y otros recursos empleados; Idoneidad Afectiva, evalúa el grado de motivación e interés de los alumnos durante la enseñanza y el aprendizaje; Idoneidad Ecológica, evalúa la adaptación del proceso de enseñanza y aprendizaje al currículo, al ideario del centro escolar, al contexto socioeconómico y al futuro laboral (Font et al., 2010). El análisis que presentamos en este trabajo se focaliza en la IE, por cuestiones de espacio, detallaremos únicamente esta idoneidad.
La IE estudia la representatividad de los distintos significados de los objetos matemáticos presentes en el proceso de instrucción. Por ejemplo, en el caso de la enseñanza de las funciones de 4º de ESO, reducir la enseñanza al aspecto operacional y a su representación algebraica (baja idoneidad) o trabajar diferentes significados de función, como correspondencia, relación entre variables, relación entre magnitudes, y sus distintas representaciones, verbal, algebraica, tabular, gráfica e icónica (alta idoneidad).
Breda et al. (2017) establecen una estructura de componentes e indicadores que orientan y organizan el análisis y la evaluación de la Idoneidad Didáctica de los procesos de estudio de cualquier etapa educativa. Es importante tener en cuenta que los componentes y también los indicadores de los CID se han configurado considerando los principios, las tendencias y los resultados de las investigaciones en Educación Matemática (Breda et al., 2018). La tabla 1 presenta los componentes e indicadores de la IE.
1.2 Investigaciones sobre la noción de función en el marco del EOS
En el marco teórico del EOS se han desarrollado diversos estudios sobre el concepto de función (Amaya de Armas et al., 2016; Flores y Font, 2017; Parra-Urrea y Pino-Fan, 2017; Pino-Fan y Parra-Urrea, 2021; Ramos y Font, 2008; Sánchez et al., 2021). Nuestra investigación se apoya en los trabajos anteriores para profundizar en la faceta epistémica de la noción de función y de los procesos implicados en su enseñanza y aprendizaje. Recogemos los listados propuestos en estas investigaciones, de clasificaciones y caracterizaciones de los procesos que están asociados a los componentes de la IE, con la finalidad de completar la iniciativa de Pino-Fan y Parra-Urrea (2021), diseñando, en este trabajo, una herramienta que adecúe los CID para analizar, evaluar y mejorar los procesos de instrucción de funciones. Esta herramienta, además, posibilitará la investigación del conocimiento meta didáctico-matemático del profesorado.
2. Metodología
Esta investigación es de tipo mixto. Se integran los métodos cuantitativo descriptivo y cualitativo. El uso de las fortalezas de ambos enfoques aumenta la calidad de las investigaciones (Leite et al., 2021). La metodología cuantitativa se aplica a la selección y la cuantificación de los TFM que han desarrollado su UD alrededor funciones en la ESO. No obstante, el enfoque cualitativo centrado en la reflexión de los profesores en formación inicial es predominante en este trabajo. De esta manera, a partir del análisis de la reflexión que los futuros docentes han incluido en sus TFM sobre la IE del diseño y de la implementación de la UD, emergen categorías inductivas de tipos de errores, ambigüedades, riqueza de procesos y representatividad de la complejidad del objeto función trabajado en la ESO. El estudio, la comparación, la generalización de estas nuevas categorías nos ha permitido diseñar una herramienta específica para la planificación, análisis y valoración de los procesos de instrucción de las funciones en la ESO.
2.1 Contexto y participantes
Los datos se refieren a 119 TFM sobre funciones en la ESO de alumnos del “Màster interuniversitari de Formació del Professorat de Secundària de Matemàtiques de Catalunya” del curso 2011-2012 al curso 2020-2021. Los alumnos del máster realizan dos fases de prácticas en centros de secundaria. El objetivo de la primera es que los profesores en formación inicial se familiaricen con el centro educativo, el alumnado y empiecen a trabajar con el mentor del centro en la UD que deben diseñar. En la segunda fase, los futuros profesores llevan a la práctica la UD que han preparado. A continuación, en el TFM, aplican los CID para analizar el grado de Idoneidad Didáctica de su propia práctica docente y rediseñan la UD para elevar el nivel de Idoneidad Didáctica. En particular, al valorar la IE, reflexionan sobre los errores, ambigüedades, riqueza de procesos y representatividad de la complejidad de las funciones.
2.2 Diseño de la herramienta Refinamiento de los Indicadores de la IE para Funciones (RIEF)
Para llevar a cabo el diseño de la RIEF hemos seguido una adaptación de los pasos del análisis temático elaborado por Braun y Clarke (2006) estructurado en seis fases. En el primer paso, se hizo un estudio bibliográfico y se consideraron los indicadores propuestos en Godino et al. (2006a), Pino-Fan y Parra-Urrea (2021) y Sánchez et al. (2021) para hacer un primer análisis de los TFM y, a partir de una triangulación de expertos de la herramienta CID, se elaboró un listado de indicadores presentes en las reflexiones y propuestas de mejora de los profesores en formación inicial. En el segundo paso, a partir de los dos listados anteriores, hemos confeccionado un único listado. En un tercer paso, hemos clasificado los indicadores por componentes del criterio de IE (errores, ambigüedades, riqueza de procesos y representatividad de la complejidad de los objetos matemáticos) y le hemos asignado un código inicial según el componente al que pertenece ((Ei), (Ai), (Pi) y (ROMi)). En el cuarto paso, hemos revisado los indicadores dentro de cada componente. Algunos indicadores no se ajustaban al componente asignado. Unos han sido eliminados y otros han dado lugar a una nueva categoría (opción didáctica adecuada (Oi), significados (Si), representaciones y conversiones (RCi) y situaciones problema (Ti)). Como se puede observar, la categoría correspondiente al criterio representatividad de la complejidad de los objetos matemáticos ha sido sustituida por tres nuevas categorías: significados, representaciones y conversiones y situaciones problema. En el quinto paso, hemos trabajado en la definición de cada uno de los indicadores de manera que sea claro y operativo. También hemos revisado la coherencia dentro de cada categoría y globalmente de toda la herramienta. Finalmente, en el sexto paso, hemos estructurado las categorías de indicadores como una pauta especializada para reflexionar sobre la enseñanza de las funciones en secundaria.
2.3 Análisis de los TFM utilizando la RIEF
En la primera fase se efectúa un análisis, cuantitativo de estadística descriptiva. En concreto se calcula la frecuencia absoluta y relativa de los TFM en los que se han identificado cada uno de los indicadores RIEF. Se distingue si está presente en el análisis de la planificación e implementación de la UD o en el rediseño. En la segunda fase, a partir de una triangulación de expertos, se realiza un análisis cualitativo, que, a partir de las evidencias presentes en los TFM, nos permite caracterizar el conocimiento meta didáctico matemático de sus autores. Estudiamos con qué grado de profundidad les ayudan a reflexionar los indicadores del criterio de la IE y cómo la pauta RIEF facilita la realización de un análisis más guiado, y, por tanto, más profundo, que contribuiría a explicitar mejor las debilidades y los logros de los procesos de instrucción.
3 Resultados
En esta investigación se han realizado tres niveles distintos de análisis. Así pues, los resultados obtenidos en cada uno de ellos son de distinta tipología. Primero se ha elaborado la pauta RIEF, después se analizan los TFM con la pauta de forma cuantitativa y, finalmente, se analizan los TFM cualitativamente.
3.1 Indicadores de la RIEF
Hemos obtenido la siguiente adecuación de la IE con la finalidad de facilitar el análisis de los procesos instrucción en la secundaria obligatoria sobre funciones.
3.1.1 Errores
(E1) “Se evita el error de utilizar curvas continuas para funciones discretas” (Pino-Fan y Parra-Urrea, 2021, p.50). (E2) Error de definición. (E3) Error de representación. (E4) Error de resolución o procedimiento. (E5) Error en la proposición de un problema. (E6) Error de argumentación.
3.1.2 Ambigüedades
(A1) Se hace uso de metáforas de forma consciente. (A2) Uso de la notación para representar la función y la imagen de un valor de la sin especificar los dos significados. (A3) Lenguaje dinámico de funciones. (A4) Imprecisión en el lenguaje. (A5) Uso de la notación para representar un punto y un intervalo sin especificar los dos significados.
3.1.3 Opción didáctica adecuada
(O1) “El trabajo con funciones no se limita al uso de representaciones algebraicas para evitar que se perciban solo como fórmulas y regularidades” (Pino-Fan y Parra-Urrea, 2021, p. 50). (O2) Se evita “la creencia de que un cambio en la variable independiente implica necesariamente un cambio en la variable dependiente” (Pino-Fan y Parra-Urrea, 2021, p. 50). (O3) “Se presentan relaciones funcionales que no son graficables para evitar la creencia de que toda función admite una representación gráfica” (Pino-Fan y Parra-Urrea, 2021, p. 50). (O4) “Se presentan relaciones funcionales que no tienen asociada una expresión algebraica para evitar la creencia de que toda función admite una representación algebraica” (Pino-Fan y Parra-Urrea, 2021, p. 50). (O5) “Las funciones se presentan con dominios y codominios explícitos para evitar la creencia de que toda función tiene un dominio y un codominio natural o real” (Pino-Fan y Parra-Urrea, 2021, p. 50). (O6) “Se presentan gráficas “irregulares” para evitar la creencia de que toda función representada gráficamente tiene “buen comportamiento” (Pino-Fan y Parra-Urrea, 2021, p. 50). (O7) “Las definiciones y los procedimientos consideran la arbitrariedad y la univalencia como características clave de la noción de función” (Pino-Fan y Parra-Urrea, 2021, p. 50). (O8) “Se presentan las nociones de dominio y codominio como elementos inherentes a la definición de función” (Pino-Fan y Parra-Urrea, 2021, p.50). (O9) “Se presentan enunciados y procedimientos fundamentales relativos a la noción de función adecuados al nivel educativo” (Pino-Fan y Parra-Urrea, 2021, p. 50). (O10) Al introducir el sistema de referencia cartesiano se tienen en cuenta las confusiones que pueden producirse (O11). Los alumnos carecen de conocimientos previos que dificultan el aprendizaje.
3.1.4. Riqueza de procesos
(P1) Se leen e interpretan correctamente los enunciados de los problemas. (P2) Se enuncian conjeturas y proposiciones. (P3) Argumentación: se justifican conjeturas y procedimientos. (P4) Se institucionalizan las definiciones y los procedimientos. (P5) Se identifican las variables y las magnitudes. (P6) Se identifica si una relación es funcional y en caso afirmativo de qué tipo es. (P7) Se aplican algoritmos, rutinas o se realizan cálculos. (P8) Se realizan procesos de generalización y abstracción.
3.1.5. Significados
(S1) “La función como correspondencia” (Pino-Fan y Parra-Urrea, 2021, p. 47). (S2) La función como relación entre variables. (S3) “La función como relación entre magnitudes” (Pino-Fan y Parra-Urrea, 2021, p. 47). (S4) “La función como correspondencia arbitraria” (Pino-Fan y Parra-Urrea, 2021, p. 47). (S5) “La función a partir de la teoría de conjuntos” (Pino-Fan y Parra-Urrea, 2021, p. 47).
3.1.6. Representaciones y conversiones
Se moviliza la representación: (R1) verbal. (R2) algebraica. (R3) tabular. (R4) gráfica. (R5) no se especifica el tipo.
Se promueven conversiones entre la representación: (R6) verbal y la algebraica. (R7) verbal y la tabular. (R8) verbal y la gráfica. (R9) algebraica y la tabular. (R10) algebraica y la gráfica. (R11) tabular y la gráfica. (R12) no se especifican los tipos.
3.1.7. Situaciones problema
Los problemas propuestos: (T1) activan las distintas significaciones de función. (T2) movilizan las distintas representaciones de función y sus conversiones. (T3) “en contextos puramente matemáticos para reforzar el aprendizaje sobre funciones” (Pino-Fan y Parra-Urrea, 2021, p. 50). (T4) donde se trabajan conexiones intramatemáticas. (T5) “contextualizados provenientes de la vida cotidiana o de otras ciencias” (Pino-Fan y Parra-Urrea, 2021, p. 50). (T6) de modelización. (T7) que impliquen los distintos tipos de funciones trabajadas.
Es relevante subrayar que la RIEF contiene la categoría Opción didáctica adecuada cuyos indicadores no corresponden a la IE, sino a la cognitiva. Pero son identificados como errores o como ambigüedades, en el análisis de la IE de los TFM. Es necesario tenerlos en cuenta para corregir esta tendencia. Como ya se ha indicado, del componente representatividad de la complejidad de los objetos matemáticos han emergido tres categorías (significados, representaciones y conversiones y situaciones) pero, en cambio, no han emergido proposiciones, ni procedimientos, ni argumentos, elementos que constituyen, junto con los tres anteriores, las configuraciones epistémicas.
3.2 Resultados obtenidos del análisis cuantitativo
Se han analizado las reflexiones sobre su propia práctica que realizan los autores de los TFM para identificar en cuáles de los anteriores indicadores se basan para proponer mejoras en sus UD.
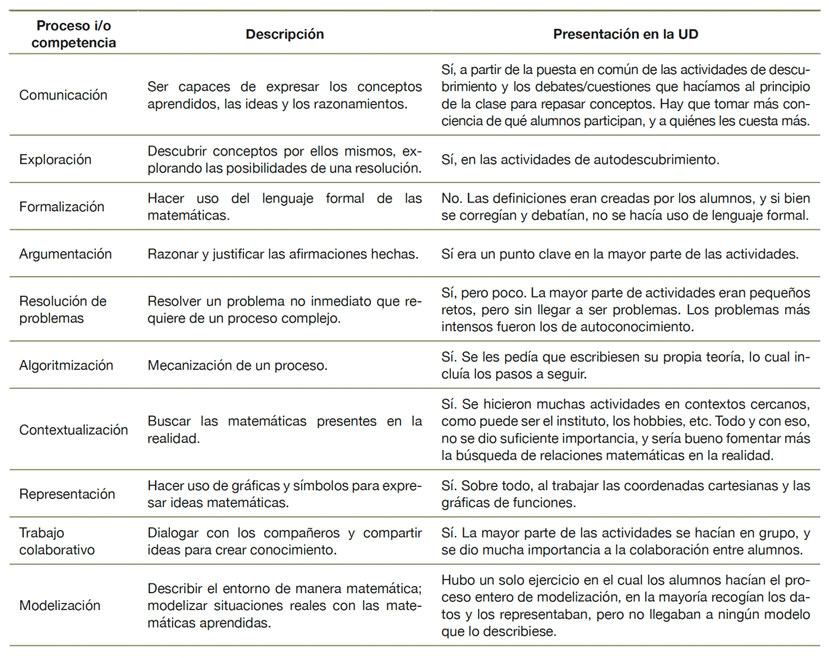
La tabla 2 muestra los datos recogidos en el análisis de los 119 TFM participantes en relación con los componentes e indicadores RIEF identificados en sus reflexiones. Hemos contabilizado el número de TFM donde se reflexiona sobre cada uno de los indicadores RIEF (I) y en qué aspectos de estos se reflexiona (diseño e implementación (D) y/o propuesta de mejora (M) de la UD). En relación con los TFM analizados, X indica que no se ha encontrado ninguna reflexión sobre el componente; F hace referencia a que el autor del TFM afirma que no detecta errores o ambigüedades; V indica que se explicita la voluntad de no cometer errores o introducir ambigüedades o potenciar procesos. Los datos de la columna F indican, para cada categoría de indicadores de la RIEF, el número de TFM que no recogen ninguna reflexión sobre esa categoría. La columna cuarta y siguientes recogen el número de TFM en los que se ha identificado cada indicador de la RIEF (ver detalle de los indicadores en sección 3.1).
Tabla 2 Número de TFM que reflexionan sobre cada indicador RIEF
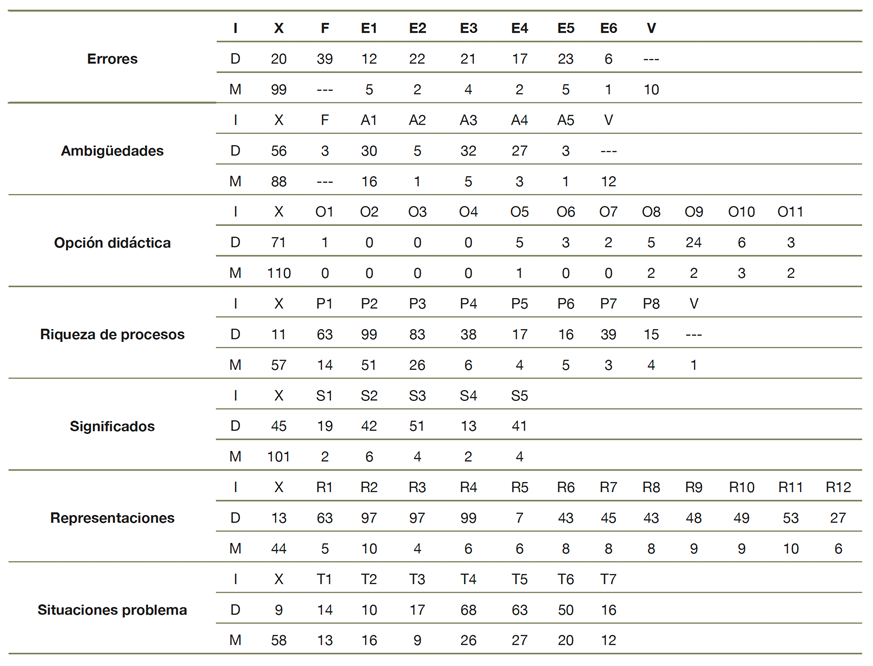
Nota . TFM (traducción de las autoras).
De la tabla 2 inferimos que en los análisis que han realizado los futuros profesores sobre sus implementaciones, muchos de los indicadores de la RIEF no son considerados. Esto se pone todavía más de manifiesto en los rediseños que proponen.
3.3 Resultados obtenidos del análisis cualitativo
En el análisis de la reflexión que efectúan los alumnos del máster en los TFM sobre funciones de la ESO se observa que los tipos de errores sobre los que más reflexionan son los que se cometen en la proposición de problemas (19 %), en definiciones (19 %) y en representaciones (18 %).
Los tipos de ambigüedad sobre los que más se reflexiona son el uso del lenguaje dinámico de funciones (27 %) y el uso de metáforas de forma consciente (25 %). Sin embargo, solo el 4 % de los futuros profesores reflexiona sobre el uso de la notación para representar la función y la imagen de un valor de sin especificar los dos significados. En el TFM 41937 se describe la siguiente ambigüedad detectada por el autor en la implementación de su UD.
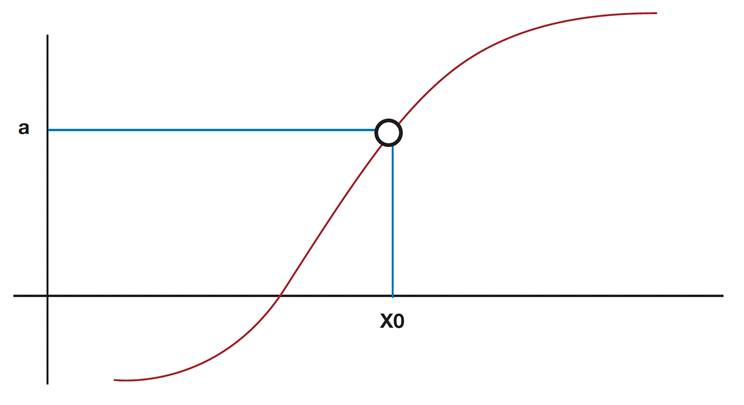
Una ambigüedad fue al explicar las funciones discontinuas, las cuales, definimos como aquellas funciones cuya gráfica no se puede dibujar sin levantar el lápiz del papel. Esta definición les generó confusión cuando dibujamos una función discontinua en la que el punto de discontinuidad se identificaba con un círculo […]. Algunos alumnos expresaron que en ningún momento se levantaba el lápiz para continuar dibujando toda la función, ya que recorrían el círculo, y por tanto no era una función discontinua.
Nota. TFM 41937 (traducción de las autoras).
La opción didáctica adecuada más presente en la reflexión de los TFM hace referencia a la adecuación al nivel educativo (20 %). El proceso más tenido en cuenta es enunciar conjeturas y proposiciones (83 %). Le sigue la justificación de conjeturas y procedimientos (70 %). La mayor parte de los futuros profesores reconoce una carencia de este tipo de procesos en el diseño e implementación de sus UD y el 52 % las introducen en sus propuestas de mejora. El autor del TFM 21708 justifica la presencia de estos procesos. Así evidencia la argumentación en su UD:
La actividad mostraba la gráfica de una función en unos ejes de coordenadas. El objetivo era escoger qué deportes (de un listado que yo les di) podrían ser representados con aquella gráfica. Los y las alumnas se vieron obligados a argumentar cuáles sí y cuáles no y por qué. (TFM 21708, traducción de las autoras)
Los significados que más aparecen en las reflexiones de los TFM son la función como relación entre magnitudes (43 %), relación entre variables (35 %) y desde la teoría de conjuntos (35 %), aunque solo un 24 % de los autores que reflexionan sobre los significados cuando analizan su UD lo hacen en sus propuestas de mejora. El 89 % de los TFM reflexionan sobre el componente representaciones y conversiones. Es en este componente donde encontramos evidencias de un análisis más detallado. Esta es la reflexión del autor del TFM 11402:
Nota. TFM 11402 (traducción de las autoras).
Como se puede observar en la figura 2, trabajamos casi todas las maneras de representación y en todas las direcciones. La manera que más trabajamos fue pasar de la forma verbal a las otras tres maneras de representación. Y la que menos utilizamos fue la expresión simbólica y su conversión a las otras, ya que los alumnos de 1º de ESO no habían estudiado las expresiones algebraicas. Podemos decir que trabajamos en 6/11 de las direcciones posibles. (TFM 11402, traducción de las autoras)
El componente situaciones problema es el que está más presente. El 92 % de los trabajos contienen reflexiones sobre alguno de sus indicadores. El más estudiado es la presentación de problemas donde se trabajan conexiones intramatemáticas (57 %) y le sigue la presentación de problemas contextualizados (53 %).
Es muy habitual que el análisis de los procesos matemáticos trabajados se limite a indicar cuáles de los descritos en la siguiente figura 3 han estado presentes en el diseño e implementación de la UD. Algunos autores justifican citando algunas actividades como ejemplo, pero sin más concreción ni profundización. La autora del TFM 21913 hace un buen análisis a partir de la pauta contenida en la figura 3, pero como esta pauta no tiene en cuenta los objetos matemáticos con los que se está trabajando, es generalista, poco refinada y no es suficiente para que los docentes constaten con precisión qué tipo de procesos están promoviendo y qué situaciones de aprendizaje hacen emerger estos procesos.
Nota. TFM 21913 (traducción de las autoras).
Ha habido muchos procesos presentes en la UD, motivo por el cual considero que es una UD rica en procesos y adecuada al nivel de 2º de ESO. (TFM 21913, traducción de las autoras)
También podemos observar que el porcentaje de TFM que reflexionan sobre un indicador al valorar la planificación y la implementación de la UD es superior a aquellos que lo utilizan para justificar las mejoras propuestas.
4. Discusión y conclusiones
En el estudio inicial de los TFM han emergido, de la reflexión de los profesores en formación inicial, los objetos primarios, significados, representaciones y conversiones y situaciones, pero, en cambio, no han emergido otros objetos primarios, como, por ejemplo, las proposiciones, los procedimientos y los argumentos, también presentes en el componente Representatividad de la Complejidad. ¿Por qué no emergen? Porque hay una falta de profundidad en la reflexión de los futuros profesores en cuanto a las proposiciones, argumentos y procedimientos. La literatura científica contiene los siguientes elementos que están relacionados con las proposiciones, procedimientos, argumentos de la noción de función: a) “los procedimientos consideran la arbitrariedad y la univalencia como características clave de la noción de función” ; b) “se presentan enunciados y procedimientos fundamentales relativos a la noción de función adecuados a nivel educativo” y; c) “se promueven situaciones en que los estudiantes deben justificar sus conjeturas y procedimientos” (Pino-Fan y Parra-Urrea, 2021, p. 50). Estos no son explicitados en los TFM que hemos analizado.
El hecho de tener únicamente como fuente de los datos los TFM de los futuros profesores es una de las limitaciones de este estudio Para poder conocer mejor el conocimiento meta didáctico matemático de los docentes sería necesario realizar estudios de caso de profesores noveles, exalumnos del máster, cuando reflexionan sobre su propia práctica docente utilizando la RIEF. Para ello, analizaríamos sus reflexiones, haríamos observaciones de aula y los entrevistaríamos para conocer con más profundidad su conocimiento meta didáctico matemático.
En el análisis de las reflexiones de los TFM sobre funciones para la etapa de la ESO, se puede afirmar que se han obtenido evidencias de casi todos los indicadores RIEF (tabla 2), en mayor o menor medida. Sin embargo, al entrar en detalle en cada TFM, se observa que, cuando los participantes revisan la UD que han diseñado y su implementación, la pauta de que disponen -los CID (tabla 1) y una pauta en referencia a los procesos (figura 3)- les ayuda a reflexionar (Esqué de los Ojos y Breda, 2021). No obstante, al no ser esta una pauta específica para la IE de las funciones (como lo es la RIEF), los participantes no atienden en su análisis a la mayoría de los RIEF. Se constata que sus reflexiones presentan importantes carencias que podrían influir en la calidad de sus procesos de instrucción.
No considerar algunos de los indicadores de la RIEF puede ser debido a una falta de conocimiento matemático ampliado de los profesores en formación como amuestran Batista et al. (2022). El uso de las RIEF ayudaría a mejorar este tipo de conocimiento sobre funciones.
Aunque la revisión de la literatura apunta que los trabajos que aplican los CID como herramienta teórico-metodológica han aumentado en los últimos años (Malet, 2022), se hacen necesarios nuevos contextos de uso y el refinamiento de las componentes para analizar procesos de enseñanza de objetos matemáticos específicos (Araya et al., 2021; Breda et al., 2021; García Marimón et al., 2021; Piñero-Charlo et al., 2021). En consecuencia, si se dotara al profesorado de herramientas como la RIEF, la reflexión sobre su propia práctica podría mejorar, ya que dispondrían de una pauta específica para realizar un análisis con más rigor, claridad y eficiencia. Como indican Pino-Fan y Parra-Urrea (2021):
Los procesos de instrucción idóneos sobre funciones requieren que los docentes conozcamos su evolución histórica; es decir, que se comprenda el significado holístico del objeto (su riqueza de significados y cómo trabajarlos y promoverlos) para tener una visión más amplia y profunda sobre la noción de función. (p. 48)
Así pues, utilizar la RIEF no solo contribuiría a la mejora de su práctica docente, sino que posibilitaría un mayor conocimiento meta didáctico-matemático de quienes la usen.
Los resultados de esta investigación dejan vislumbrar que al avanzar los niveles educativos aparecen nuevas nociones matemáticas asociadas a la de función (pendiente, continuidad, monotonía, concavidad, etc.) para las que también es necesario desarrollar una herramienta refinada.
Los cursos de formación de futuros docentes podrían enriquecerse con un módulo en el que se enseñase la RIEF para mejorar su conocimiento sobre funciones al considerar todos los significados, representaciones, procesos involucrados en la complejidad de las funciones y las prácticas matemáticas en las que estos emergen. Y también profundizarían en el tipo de reflexión requerida para diseñar, implementar y reflexionar sobre sus procesos de instrucción.