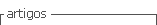Forma sugerida de citar:
Araújo, S., Viseu, F., Soares, A. J. y Leite, I. (2022). El aprendizaje de las funciones logarítmicas por parte de estudiantes de 12º grado basado en tareas de modelización. Alteridad, (17) 2, 224-243. https://doi.org/10.17163/alt.v17n2.2022.05
1. Introducción
Al racionalizar las actividades de aprendizaje de los temas matemáticos, las características de las tareas exploradas adquieren relevancia al desafiar a los y las estudiantes a comprometerse y reflexionar sobre lo que hacen en estas actividades (Tekkumru-Kisa, 2020). Estas características distinguen las tareas en cuanto al grado de desafío, alto o bajo, y al grado de estructuración, abierta o cerrada (Ponte, 2005). Entre las tareas comúnmente trabajadas en las clases de matemáticas, podemos destacar los ejercicios (bajo nivel de desafío y estructura cerrada), los problemas (alto nivel de desafío y estructura cerrada) y las tareas de investigación (alto nivel de desafío y estructura abierta). Integradas en estas tipologías se encuentran las tareas de modelización, en forma de problemas o investigaciones, dependiendo del grado de estructura de su enunciado. La actividad resultante de la resolución de este tipo de tareas se denomina modelización matemática, que actualmente forma parte de los currículos de matemáticas de varios países (Chong et al., 2019; Hoe y Dawn, 2015). En Portugal, forma parte del perfil de los alumnos que salen de la enseñanza obligatoria (Ministério da Educação, 2017). Dawn (2018) y Stillman et al. (2017) sostienen que la modelización debe formar parte de las actividades realizadas en la escuela en el aprendizaje de las ciencias.
En cuanto a la asignatura de Matemáticas, el Programa para la Evaluación Internacional de Alumnos (PISA: Programme for International Student Assessment) contempla la definición de actividades de alfabetización matemática relacionadas con la modelización:
La alfabetización matemática es la capacidad de un individuo para formular, aplicar e interpretar las matemáticas en una variedad de contextos. Incluye el razonamiento matemático y el uso de conceptos, procesos, hechos y herramientas matemáticas para describir, explicar y predecir fenómenos. (OECD, 2019, p. 75)
Hay varios autores (por ejemplo, Shahbari y Tabach, 2020; Viseu y Rocha, 2020) y obras de referencia (por ejemplo, NCTM, 2000) que defienden la contribución de la modelización matemática en el desarrollo de habilidades críticas para el compromiso del alumnado en sus actividades futuras (Reys-Cabrera, 2022). El NCTM (2000) recomienda que los alumnos experimenten con la modelización matemática de problemas del mundo real, tanto sociales como físicos, a lo largo de su escolaridad, y esta práctica debería estar más presente en los últimos cursos.
Un tema favorito de las matemáticas para modelar fenómenos son las funciones (Viseu y Rocha, 2020). Desde la escuela primaria, los y las estudiantes trabajan con relaciones entre cantidades, como la proporcionalidad entre cantidades, a través de, por ejemplo, un problema que involucra la velocidad de los automóviles, o funciones cuadráticas, a través de problemas de optimización de áreas de figuras geométricas (Rocha, 2019). En el bachillerato se introducen conceptos matemáticos de gran alcance, como la derivación, que permite describir y comprender funciones más complejas. De estas funciones, tenemos las funciones logarítmicas introducidas en el 12º grado[1] de secundaria. Numerosos fenómenos cotidianos pueden modelizarse mediante estas funciones, como el crecimiento de una población bacteriana o la magnitud de un terremoto. Enfrentarse a un problema de modelización matemática es esencial para comprender y estructurar las matemáticas presentes en el problema. En la resolución de algunas de estas tareas, las funciones son esenciales para representar y resolver problemas de la vida real (Sawalha, 2018), como ocurre con las funciones logarítmicas que se traducen en numerosas situaciones cotidianas. Según Kastberg (2002) y Weber (2002), los y las estudiantes tienen dificultades para comprender y representar las funciones logarítmicas porque la exploración de las funciones logarítmicas se limita principalmente a los aspectos teóricos. Además, la escritura simbólica de los logaritmos y, en consecuencia, de las funciones logarítmicas tiende a perturbar su comprensión (Mulqueeny, 2012). La enseñanza de estas funciones a través de problemas y situaciones de la vida real puede mejorar la comprensión de los alumnos de sus temas de estudio. Por lo tanto, es fundamental realizar estudios que profundicen los conocimientos potenciando esta comprensión (Viseu y Rocha, 2020).
Para ello, la tecnología es primordial para identificar y visualizar el modelo que mejor se ajusta al contexto del problema en estudio. La calculadora gráfica es indispensable para conceptualizar y comprender las diferentes representaciones de una función (Viseu y Menezes, 2014; Viseu et al., 2020). La relevancia de este dispositivo didáctico aumenta al permitir conectar las representaciones analíticas y gráficas de los conceptos de funciones logarítmicas y conjeturar resultados. En la realización de las tareas de modelización en el aprendizaje de los temas de las funciones logarítmicas en estudio, la calculadora gráfica es un material didáctico que proporciona al alumnado el uso de tablas, la edición de gráficos y la exploración de las curvas de regresión que mejor se ajustan a los datos resultantes de las tareas propuestas en clase (Viseu y Menezes, 2014).
La combinación de la resolución de tareas de modelización matemática utilizando la calculadora gráfica pone de manifiesto la valoración de la aplicación de lo que el alumno aprende en la resolución de situaciones problemáticas de la realidad, su implicación en las actividades que se proponen en la clase de matemáticas y dar sentido a lo que aprende (Viseu y Rocha, 2020).
A partir de estos supuestos, este trabajo tiene como objetivo caracterizar las actividades que los alumnos de 12º grado realizan con las tareas de modelización matemática en el aprendizaje de las funciones logarítmicas e identificar las dificultades que tienen en esta resolución, utilizando la calculadora gráfica.
1.1. Modelización matemática
En los últimos años, el uso de modelos matemáticos en la enseñanza y aprendizaje de materias científicas ha sido objeto de varios estudios (Anhalt et al., 2018; Stillmann et al., 2017). Las conexiones entre las matemáticas y el mundo natural condicionan la enseñanza y el aprendizaje de las matemáticas (Barbosa, 2006, 2009; Blum, 2002). Dentro de la investigación, ha llamado la atención el impacto de la modelización matemática en la enseñanza en todos los grados (Stillman et al., 2007). Es fundamental analizar en la literatura cómo el modelado matemático apoya el desarrollo de habilidades en la educación de los alumnos (Kaiser & Sriraman, 2006; Kaiser y Maaß, 2007; Karawitz y Schukajlow, 2018). El primer impase a superar es definir la modelización matemática, distinguiéndola de la matemática aplicada. Según Blum (2002), Blum et al. (2007) y Stillman et al. (2007), las matemáticas aplicadas se centran en el uso de herramientas matemáticas en una situación determinada del mundo real. La modelización matemática se centra, a su vez, en la identificación y el desarrollo de herramientas matemáticas que ayuden a resolver ese problema (Verschaffel, 2000). La modelización matemática es un proceso de resolución de problemas del contexto real (Carreira y Blum, 2021).
La intención de la modelización matemática puede interpretarse de diversas maneras. Algunos autores la interpretan como un vector de motivación para introducir, desarrollar y consolidar el conocimiento y el aprendizaje matemático (Barbosa, 2009). Otros lo interpretan como un enfoque puramente educativo para desarrollar la capacidad de los alumnos de resolver problemas concretos (Galbraith y Stillman, 2006). Aunque se trata de interpretaciones diferentes, no están disociadas. Al abordar un problema de modelización matemática centrándose en los procesos de resolución, se pueden alcanzar los objetivos de aprendizaje de determinados contenidos (Barbosa, 2009; Galbraith y Stillman, 2006).
La resolución de un problema de modelización matemática requiere comprender e interpretar el contexto de la situación estudiada e identificar los principales aspectos del problema. Para ello, se pueden recoger datos y describir y comprender las relaciones y los patrones entre las cantidades para traducir esta información al lenguaje matemático (Blum, 2002). Esta estructura matemática se denomina modelo matemático (Blum, 2002; Lesh y Fennewwald, 2010). El desarrollo de un modelo puede realizarse a través de diversas representaciones para abarcar el posible potencial de respuestas a una situación determinada (Lesh y Fennewwald, 2010).
Así, los modelos recorren diferentes dimensiones, de lo concreto a lo abstracto, de lo específico a lo general, de lo global a lo analítico, de lo simple a lo complejo, de lo situacional a lo descontextualizado y de lo intuitivo a lo formal (Lesh & Fennewwald, 2010). La aplicación de un modelo matemático para estudiar un problema prevé el uso de herramientas y métodos matemáticos conocidos para extraer resultados matemáticos de ese modelo. A su vez, estos resultados deben ser interpretados y validados analizando su relevancia para el contexto y el propósito del problema real. Este proceso puede repetirse, desde cero, en la definición del modelo, en función de su eficacia como solución al problema (Blum, 2002; Greefrath, 2019; Stillman et al., 2007). Este proceso se denomina modelización matemática, que se traduce en la identificación y definición de sus fases y transiciones en diversos diagramas o esquemas. Stillman et al. (2007) adaptaron un diagrama de Galbraith y Stillman (2006) para representar el ciclo de modelado matemático, incorporando el razonamiento que se produce entre las distintas fases (figura 1).
En este diagrama, las letras A-G representan las fases del proceso de modelización, y las flechas las transiciones entre las fases: (1) Comprender, estructurar, simplificar, interpretar el contexto; (2) Suponer, formular, matematizar; (3) Desarrollar y explorar matemáticamente; (4) Interpretar los resultados matemáticos; (5) Comparar, criticar, validar; (6) Comunicar, justificar (si el modelo se considera satisfactorio); (7) Volver a pasar por el proceso de modelización (si el modelo se considera insatisfactorio).
Para Borromeo Ferri (2006), no siempre es de interés para el alumno pasar por todas las fases del ciclo de modelización en el aprendizaje de contenidos matemáticos, y hay que intentar adaptar este ciclo al contexto del aula. Los autores identifican, a partir de estudios y datos empíricos, los aspectos críticos que pueden bloquear a los alumnos en una determinada fase. Estos datos fueron recogidos en el contexto del aprendizaje de contenidos matemáticos mediante la modelización de problemas y el uso de herramientas tecnológicas (Galbraith y Stillman, 2006; Stillman et al., 2007). Del análisis de estos datos se desprende que entre las principales dificultades de estudiantes se encuentran la comprensión del enunciado y su contexto (Galbraith y Stillman, 2006; Stillman et al., 2007), la identificación de las variables dependientes e independientes, la elaboración del modelo, así como la estructura matemática del problema real (Dede, 2016; Galbraith y Stillman, 2006; Shahbari y Tabach, 2020).
1.2. Funciones logarítmicas
Las funciones logarítmicas son esenciales en el cálculo infinitesimal y la modelización matemática porque aparecen asociadas a diversos fenómenos naturales, como la medición de la amplitud de un terremoto en la escala de Richter (Weber, 2017).
La comprensión del concepto de función logarítmica se convierte en algo esencial para preparar al alumnado a enfrentarse a problemas concretos (Kenney y Kastberg, 2013). Formalmente, en los programas escolares, la función logarítmica está definida como la función inversa de la función exponencial. Más concretamente, una función logarítmica de base a se define por 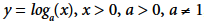 , siendo
, siendo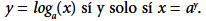 De forma análoga, las funciones exponenciales, la comprensión de las funciones logarítmicas implica la capacidad de interpretar la notación utilizada (Kenney y Kastberg, 2013; Weber, 2017). En la expresión
De forma análoga, las funciones exponenciales, la comprensión de las funciones logarítmicas implica la capacidad de interpretar la notación utilizada (Kenney y Kastberg, 2013; Weber, 2017). En la expresión 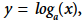 percibir la dualidad entre el objeto
percibir la dualidad entre el objeto 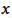 como elemento del dominio de la función es y cómo el número obtenido en la forma
como elemento del dominio de la función es y cómo el número obtenido en la forma 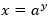 es un obstáculo para la mayoría de los y las estudiantes (Weber, 2002). Dado que la notación
es un obstáculo para la mayoría de los y las estudiantes (Weber, 2002). Dado que la notación 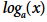 es relativamente atípica en comparación con las funciones algébricas, resulta confuso para la mayoría de estudiantes asociar propiedades y características específicas (Kenney y Kastberg, 2013). La falta de comprensión de la notación de las funciones logarítmicas, en concreto de las bases y de las diferentes nomenclaturas
es relativamente atípica en comparación con las funciones algébricas, resulta confuso para la mayoría de estudiantes asociar propiedades y características específicas (Kenney y Kastberg, 2013). La falta de comprensión de la notación de las funciones logarítmicas, en concreto de las bases y de las diferentes nomenclaturas  puede dificultar el aprendizaje de sus propiedades algebraicas. El alumnado puede ser capaz de interpretar funciones lineales, cuadráticas e incluso exponenciales porque sus expresiones algebraicas indican en cierto modo cuál es el proceso subyacente. Sin embargo, la notación simbólica de las funciones logarítmicas es más compleja y ambigua (Mulqueeny, 2012). Ante una ecuación logarítmica, los alumnos tienden a anular los logaritmos de la misma base como si fueran funciones polinómicas (Kenney y Kastberg, 2013). Esto demuestra que los alumnos tienen dificultades para percibir el papel de las funciones logarítmicas como funciones inversas de las funciones exponenciales. Esta dificultad también se percibe en la representación gráfica, ya que coinciden con la representación gráfica de las funciones logarítmicas con la de las funciones exponenciales (Weber, 2017). Un refuerzo de la dualidad entre una función biyectiva y su inversa a través de, por ejemplo, la raíz cuadrada y la función cuadrática, puede mejorar el aprendizaje de las funciones logarítmicas (Kenney y Kastberg, 2013). Según Sawalha (2018), proporcionar a los alumnos tareas de modelización en el aprendizaje de las funciones exponenciales y logarítmicas favorece la estructuración y comprensión de estos conceptos.
puede dificultar el aprendizaje de sus propiedades algebraicas. El alumnado puede ser capaz de interpretar funciones lineales, cuadráticas e incluso exponenciales porque sus expresiones algebraicas indican en cierto modo cuál es el proceso subyacente. Sin embargo, la notación simbólica de las funciones logarítmicas es más compleja y ambigua (Mulqueeny, 2012). Ante una ecuación logarítmica, los alumnos tienden a anular los logaritmos de la misma base como si fueran funciones polinómicas (Kenney y Kastberg, 2013). Esto demuestra que los alumnos tienen dificultades para percibir el papel de las funciones logarítmicas como funciones inversas de las funciones exponenciales. Esta dificultad también se percibe en la representación gráfica, ya que coinciden con la representación gráfica de las funciones logarítmicas con la de las funciones exponenciales (Weber, 2017). Un refuerzo de la dualidad entre una función biyectiva y su inversa a través de, por ejemplo, la raíz cuadrada y la función cuadrática, puede mejorar el aprendizaje de las funciones logarítmicas (Kenney y Kastberg, 2013). Según Sawalha (2018), proporcionar a los alumnos tareas de modelización en el aprendizaje de las funciones exponenciales y logarítmicas favorece la estructuración y comprensión de estos conceptos.
Las recomendaciones actuales para la educación matemática apuntan al desarrollo de competencias que los alumnos deben adquirir en su escolaridad (por ejemplo, NCTM, 2007). Según Niss y Højgaard (2019), la competencia matemática es la capacidad de responder con prontitud y perspicacia a cualquier desafío matemático. Los autores subrayan la diferencia entre la competencia matemática y una competencia matemática, siendo esta última la capacidad de responder con prontitud y perspicacia a un reto matemático específico. La competencia matemática, por su parte, es una unión de habilidades matemáticas (Niss y Højgaard, 2019). Para definir estos subconjuntos de competencias matemáticas, los autores subrayan que estos deben satisfacer la plenitud de las actividades matemáticas. Una actividad matemática es la acción dirigida a hacer y responder preguntas en o a través de las matemáticas (Niss y Højgaard, 2019, p. 14). A partir de estos supuestos, Niss y Højgaard (2019) definen cuatro competencias que son esenciales para participar de manera eficiente en una actividad matemática: el pensamiento matemático fundamental; la elaboración y resolución de problemas matemáticos; el uso de modelos y la modelización matemática; y el razonamiento matemático. El dominio del lenguaje matemático, de los constructos y de las herramientas permite un mayor rendimiento en la realización de actividades matemáticas, que los autores traducen como otras competencias, destrezas: el manejo de las representaciones matemáticas; el manejo de los símbolos y formalismos matemáticos; la comunicación matemática; el manejo de los recursos materiales y de las herramientas matemáticas. Los autores subrayan que todas estas competencias son distintas, pero no están disociadas.
Por ello, hemos optado por dar especial relevancia a tres competencias que consideramos fundamentales en la modelización matemática: el tratamiento de los modelos y la modelización matemática; el tratamiento de las representaciones matemáticas; el tratamiento de los recursos materiales y las herramientas matemáticas. La primera se centra en la capacidad de construir modelos matemáticos y de analizar y evaluar modelos ya definidos, teniendo en cuenta diversos factores externos como datos, hechos, propiedades y el contexto de la situación. La capacidad de articular las diferentes fases del proceso de modelización se incluye en esta competencia (Stillman et al., 2007). La competencia en el manejo de diferentes representaciones matemáticas consiste en la capacidad de interpretar y traducir los objetos, fenómenos, correspondencias y procesos matemáticos en una variedad de representaciones equivalentes, teniendo en cuenta las ventajas y limitaciones de cada una en la realización de una actividad matemática. La elaboración, el análisis y la interpretación de modelos están directamente relacionados con la manipulación de representaciones matemáticas (NCTM, 2000; Shahbari y Tabach, 2020). Por último, la tecnología es esencial como recurso constructivo y crítico en la realización de una actividad matemática. Esta competencia también considera las ventajas y limitaciones de estas herramientas para utilizarlas puntualmente en función de la actividad matemática (Niss y Højgaard, 2019).
2. Metodología
Este estudio tiene como objetivo caracterizar las actividades de los alumnos de 12º grado con tareas de modelización matemática en el aprendizaje de funciones logarítmicas e identificar las dificultades que tienen en la resolución de estas tareas utilizando la calculadora gráfica. Dichas dificultades ponen de manifiesto las acciones cognitivas que el alumnado no realiza adecuadamente en la resolución de dichas tareas o que se traducen en resoluciones erróneas (Heyd-Metzuyanim, 2013) y en un uso inadecuado de la calculadora gráfica en dicha resolución. Dados estos objetivos, uno de los autores realizó una experiencia docente basada en el uso de tareas de modelización en la enseñanza de temas de funciones logarítmicas utilizando la calculadora gráfica como parte de sus prácticas pedagógicas en el último curso del máster de formación del profesorado, que integró en sus estrategias docentes. Este dispositivo forma parte del material didáctico que los alumnos de secundaria en Portugal utilizan en la realización de sus actividades. El estudio de las funciones logarítmicas se realiza por primera vez en la trayectoria escolar de los alumnos en el 12º curso. Esta experiencia de enseñanza ocurrió durante cuatro lecciones e incluyó tareas de modelización, de las cuales seleccionamos tres (Anexos).
Para optimizar el aprendizaje de los alumnos en la resolución de las tareas de modelización, la experiencia docente desarrollada trazó estrategias que valoraban la actividad del alumno mediante un formato de enseñanza exploratoria (Ponte, 2005). En la primera fase de las lecciones, se presentaba la tarea a la clase para determinar si los alumnos entendían el enunciado de la tarea, los datos y lo que se pretendía determinar. En la segunda fase, los alumnos realizaron la tarea de forma autónoma, en par o en grupos. En este punto de la lección, el profesor apoyaba a los alumnos, pero de forma que no interfiriera en sus estrategias de resolución. Una vez finalizado el trabajo autónomo de los alumnos, se recogían sus resoluciones para que no se modificaran en función de la discusión del grupo de clase. En la penúltima fase, el profesor orquestó esta discusión con cuidado para gestionar las intervenciones de los alumnos y comparar las diferentes resoluciones. En la última fase, a partir de lo que los alumnos hacían o decían, se institucionalizaban nuevos conceptos o procedimientos producto de la exploración y discusión de la tarea.
La clase en la que se realizó esta experiencia era una clase de Ciencias y Tecnología de 12º curso, con 31 alumnos, 14 chicos y 17 chicas de entre 16 y 18 años. La clase no tenía alumnos repitientes y estaba compuesta por estudiantes que, en su mayoría, consideraban las Matemáticas y la Físico-Química como sus asignaturas favoritas. En cuanto al rendimiento en Matemáticas, las notas de los alumnos al final del curso oscilaron entre 6 y 20, con una media de aproximadamente 14,4 (DP=4,21)). En cuanto a la resolución de tareas de modelización, los alumnos ya habían realizado en cursos anteriores tareas de esta naturaleza con el profesor de la clase en el estudio de funciones polinómicas y funciones racionales.
Dada la naturaleza del objetivo planteado, se adoptó un enfoque cualitativo e interpretativo para comprender la actividad de los alumnos en la resolución de las tareas propuestas en el contexto del aula (Bogdan y Biklen, 1994). Para ello, se recogieron datos a través de los registros escritos que los alumnos produjeron en la resolución de las tareas propuestas, utilizando la calculadora gráfica para estudiar temas de funciones logarítmicas antes de su discusión en el grupo de clase. Dichas tareas se desarrollaron con la intención de que, a partir de su resolución, los alumnos adquirieran la noción de logaritmo de un número en una base determinada, realizaran el estudio de una función logarítmica, determinaran la derivada de la función logarítmica y sistematizaran el estudio de la función logarítmica.
El análisis de datos se basó en el análisis de contenido de las resoluciones de los alumnos de las tareas de modelización que se les propusieron, traduciéndose según los temas que se impartieron: (i) Introducción al estudio de la función logarítmica; (ii) Introducción a la derivada de la función logarítmica; y (iii) Sistematización del conocimiento de las funciones logarítmicas. En cada uno de estos temas se adoptan las fases de modelización consideradas desde el marco teórico: (1) comprensión del enunciado de la tarea; (2) análisis de datos/construcción y validación del modelo; (3) exploración del modelo. El análisis de las resoluciones de los alumnos permite identificar las actividades que realizaron en cada una de estas fases de modelización y las dificultades que mostraron en sus resoluciones. Este análisis se centra en las resoluciones realizadas en par en las tareas de modelización relativas a la introducción de la función logarítmica y su derivada y por grupos en la tarea de modelización relativa al conocimiento de sistematización de las funciones logarítmicas.
3. Resultados
3.1. Introducción al estudio de la función logarítmica
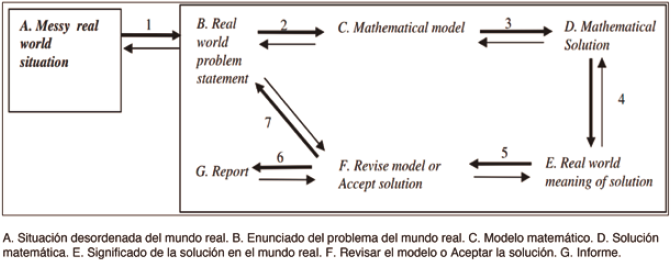
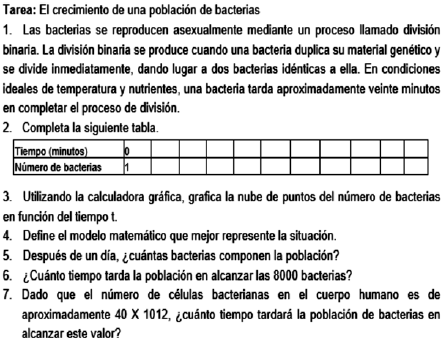
En la introducción al estudio de la función logarítmica, los alumnos comenzaron resolviendo, en par, una tarea de modelización que implicaba el conocimiento de la función exponencial previamente estudiada. La elección de esta función como modelo que surge de la resolución de la tarea propuesta se debió a la relación entre la función exponencial, con una base real positiva dada distinta de uno, y su función inversa, la función logarítmica con la misma base (tarea 1, anexos). En la exploración de esta tarea, los alumnos indicaron que interpretaron lo que la tarea preveía y les pedía. En las fases de análisis de datos, construcción del modelo y validación, los alumnos pretendían desarrollar un modelo matemático que representara la situación de la tarea. Las preguntas 2 y 3 de la tarea completan e ilustran estas fases. Los alumnos utilizaron esquemas para organizar los datos en la calculadora gráfica, identificando las variables dependiente e independiente. El par P3 recurrió a esquemas de acción instrumentados de la calculadora gráfica para obtener un modelo lineal y representó un esquema de la nube de puntos del número de bacterias en función del tiempo. Aunque en este croquis se observa una curva exponencial, definieron un modelo lineal. Esto demuestra que no percibieron bien el papel del coeficiente de determinación Importar imagen o que estos alumnos no intentaron averiguar otros modelos (figura 2).
Asimismo, al definir el mejor modelo que se ajusta a los datos, los pares P11 y P13 no recurrieron a la calculadora gráfica y definieron un modelo matemático mediante procesos algebraicos a partir de los datos de la tabla. Estos alumnos reconocieron en los datos una progresión geométrica de razón 2 y término general Importar imagen, donde n representa el número de procesos de división binaria ocurridos, lo que les permitió definir las siguientes funciones: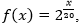 donde
donde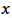 es el tiempo en minutos (P13);
es el tiempo en minutos (P13); 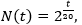 donde t es el tiempo en minutos (P11). Estos modelos se corresponden perfectamente con los datos de la tabla y el proceso de división binaria si se trabaja con modelos discretos en lugar de continuos.
donde t es el tiempo en minutos (P11). Estos modelos se corresponden perfectamente con los datos de la tabla y el proceso de división binaria si se trabaja con modelos discretos en lugar de continuos.
El par P7 identificó el modelo exponencial como el que mejor se ajustaba, basándose en el coeficiente de determinación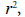 pero no reconoció que ambos modelos mostrados en la pantalla
pero no reconoció que ambos modelos mostrados en la pantalla 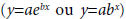 representaban el mismo modelo. Para determinar cuál se ajustaba mejor a los datos, estos alumnos recurrieron al menú de recursión de la calculadora gráfica y trazaron los dos modelos en función de
representaban el mismo modelo. Para determinar cuál se ajustaba mejor a los datos, estos alumnos recurrieron al menú de recursión de la calculadora gráfica y trazaron los dos modelos en función de  en una tabla para comparar sus valores.
en una tabla para comparar sus valores.
Algunos alumnos se mostraron críticos con los modelos obtenidos con la calculadora gráfica e intentaron comprobar los resultados utilizando otra función de la calculadora gráfica (figura 3).
Al explorar el modelo para responder a los ítems restantes, cabe destacar que los pares P11 y P13, definieron con papel y lápiz el mismo modelo exponencial 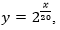 intentaron resolver esta pregunta de forma analítica. Descompusieron el número 8000 en factores primos para resolver la ecuación
intentaron resolver esta pregunta de forma analítica. Descompusieron el número 8000 en factores primos para resolver la ecuación  Sin embargo, la descomposición obtenida, 26 x 53, fue un callejón sin salida para estos alumnos. El Par P13 utilizó la calculadora gráfica para resolver la ecuación gráficamente.
Sin embargo, la descomposición obtenida, 26 x 53, fue un callejón sin salida para estos alumnos. El Par P13 utilizó la calculadora gráfica para resolver la ecuación gráficamente.
La resolución de las preguntas 5 y 6 de la tarea condujo al proceso inverso subyacente a la función exponencial para determinar el valor de 𝑥 resolviendo la ecuación. La aplicación de las propiedades de las funciones inversas, es decir, la representación gráfica de una función comparada con su función inversa, permitió a la calculadora gráfica representar la curva simétrica de la gráfica de la función exponencial determinada por la recta de ecuación  Así, se estableció la relación recíproca entre la función exponencial y la función logarítmica con la misma base:
Así, se estableció la relación recíproca entre la función exponencial y la función logarítmica con la misma base: Para sistematizar estos conocimientos, los alumnos resolvieron tareas sobre la noción de logaritmo de un número en una base determinada y sobre el estudio de las funciones logarítmicas.
Para sistematizar estos conocimientos, los alumnos resolvieron tareas sobre la noción de logaritmo de un número en una base determinada y sobre el estudio de las funciones logarítmicas.
3.2. Introducción a la derivada de la función logarítmica
La introducción a la derivada de la función logarítmica resultó de la resolución de una tarea de modelización sobre la intensidad del sonido en decibelios (tarea 2, anexo). A partir de los datos de la tabla y de la calculadora gráfica, los alumnos debían identificar el modelo que mejor se ajustaba a los datos presentados y responder a las preguntas restantes basándose en ese modelo. Esta tarea se resolvió en parejas, y las conclusiones se discutieron y analizaron en el grupo de clase.
La interpretación del enunciado de la tarea no suscitó ninguna duda en los alumnos; ninguna pareja cuestionó el significado de la expresión escala lineal contenida en la pregunta. La mayoría de las parejas no encontró dificultad en comprobar la veracidad del enunciado de Bell, reconociendo que, para que los datos verifiquen una escala lineal, debe existir una relación de proporcionalidad directa entre ellos, como ilustra la afirmación de P1: El enunciado es verdadero, dado que no es posible verificar una relación de proporcionalidad directa entre las dos variables presentes en la tabla.
Aunque los alumnos ya habían realizado una actividad de modelización matemática, la noción de modelo matemático no estaba clara para todos, así como el uso de la calculadora gráfica para determinar este modelo. Ocho parejas de alumnos (de quince) identificaron correctamente el papel de cada variable en la situación de la tarea, organizaron correctamente los datos en la calculadora gráfica y encontraron que el modelo logarítmico era el que mejor se ajustaba a los datos. Algunos alumnos no pudieron encontrar el modelo correcto porque invirtieron las variables o las listas en la tabla del menú de estadística. Por defecto, la lista 1 se asigna a la variable independiente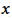 y la lista 2 a la variable dependiente
y la lista 2 a la variable dependiente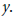 En el caso de esta tarea, la primera columna de la tabla de datos corresponde a la variable dependiente y la segunda a la variable independiente. Al invertir el papel de las variables, estos alumnos obtuvieron de forma natural un modelo exponencial. Sin embargo, otros alumnos no reconocieron el papel de las cantidades en juego y representaron gráficamente la nube de puntos de la relación
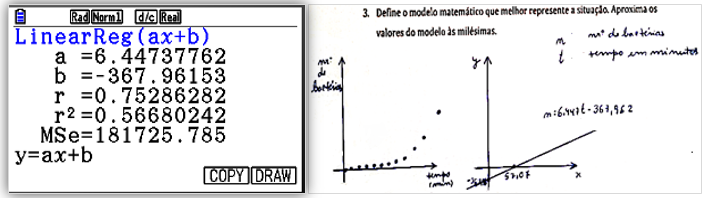
En el caso de esta tarea, la primera columna de la tabla de datos corresponde a la variable dependiente y la segunda a la variable independiente. Al invertir el papel de las variables, estos alumnos obtuvieron de forma natural un modelo exponencial. Sin embargo, otros alumnos no reconocieron el papel de las cantidades en juego y representaron gráficamente la nube de puntos de la relación 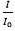 en función de la intensidad sonora en dB, lo que indujo un modelo exponencial, como ejemplifica la respuesta dada por el par P13 (figura 4).
en función de la intensidad sonora en dB, lo que indujo un modelo exponencial, como ejemplifica la respuesta dada por el par P13 (figura 4).
En cuanto a la exploración del modelo, a las parejas que definieron un modelo exponencial les resultó difícil responder a los ítems restantes. En el ítem 3, con el modelo exponencial, hay que calcular la variación en el intervalo 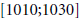 . Sin embargo, la calculadora gráfica no permite realizar este tipo de cálculo. Esto indica que estos estudiantes se enfrentaron a algunas limitaciones de la calculadora gráfica.
. Sin embargo, la calculadora gráfica no permite realizar este tipo de cálculo. Esto indica que estos estudiantes se enfrentaron a algunas limitaciones de la calculadora gráfica.
Además de las limitaciones técnicas, también se observan limitaciones debidas a ciertos conceptos matemáticos, como la definición de tasa de variación instantánea en un punto. En cuanto al apartado 4, al no haberse introducido aún la primera derivada de las funciones logarítmicas, los alumnos no tuvieron la posibilidad de resolverlo analíticamente. Cinco pares de alumnos reconocieron que podían utilizar la calculadora gráfica para determinar la tasa de variación instantánea del modelo en el punto de abscisa 15, como revela la respuesta del par P1: Utilizando la derivada de la función logarítmica (en la gráfica de mi calculadora) es posible determinar la tasa de variación instantánea de la intensidad del sonido cuando 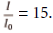 La respuesta de este par de alumnos sirvió de lema para la introducción de la derivada de la función logarítmica que modelizó la situación de la tarea mediante la definición formal de la primera derivada de una función:
La respuesta de este par de alumnos sirvió de lema para la introducción de la derivada de la función logarítmica que modelizó la situación de la tarea mediante la definición formal de la primera derivada de una función: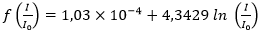 . A continuación, se definió la primera derivada de cualquier función logarítmica de base mediante las propiedades algebraicas de los logaritmos y las correspondientes reglas de derivación.
. A continuación, se definió la primera derivada de cualquier función logarítmica de base mediante las propiedades algebraicas de los logaritmos y las correspondientes reglas de derivación.
3.3. Sistematización del conocimiento de funciones logarítmicas
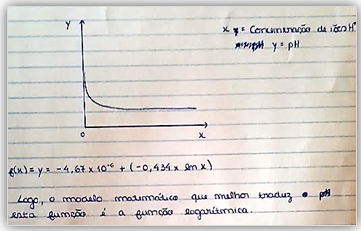
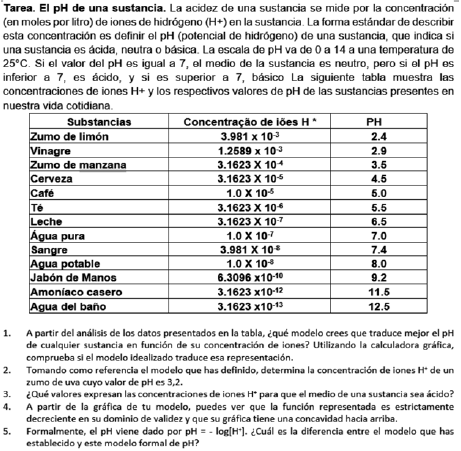
Tras la introducción de la función logaritmo y su derivada, con dos tareas de modelización en las dos primeras lecciones, se procedió a la aplicación de los conocimientos adquiridos en el estudio de la función logaritmo mediante la resolución de tareas, como ejemplifica la tarea 3 sobre El pH de una sustancia, en grupos de 3 o 4 alumnos. Todos los y las estudiantes determinaron un modelo logarítmico como el que mejor se ajusta a los datos de la tabla. Sin embargo, solo la mitad de los grupos determinó el mejor modelo logarítmico, como ilustra la respuesta del grupo G2 (figura 5).
Los grupos que respondieron incorrectamente determinaron un modelo logarítmico que no corresponde al que mejor se ajusta a los datos del enunciado. Probablemente estos grupos se equivocaron al definir y organizar los datos en la calculadora gráfica. Uno de estos grupos, el grupo G6, determinó los coeficientes correctos del modelo logarítmico esperado, pero le resultó difícil traducir estos valores al modelo que sugería la calculadora gráfica. Al leer los coeficientes del modelo logarítmico obtenido, estos alumnos no identificaron que solo el coeficiente Importar imagen multiplicaba el logaritmo neperiano de 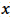 .
.
En cuanto al apartado 3, se observa que la mayoría de los grupos intentaron resolverlo con métodos exclusivamente analíticos. Sin embargo, ningún grupo llegó al resultado esperado porque los alumnos no determinaron el dominio del modelo logarítmico del pH, considerando que solo podía tomar valores entre 0 y 14. Solo un grupo restringió el dominio del modelo logarítmico considerando la situación de la tarea. El grupo G4 resolvió previamente la ecuación 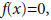 donde
donde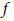 representa el modelo obtenido, para determinar el dominio del modelo. Basados en los datos de la tabla se determinó los valores de Importar imagen por los que una solución tiene un pH de tipo ácido. El modelo logarítmico se traduce en una función estrictamente decreciente, lo que repercutirá en el orden de la desigualdad que traduce el enunciado. Los grupos que respondieron incorrectamente tuvieron dificultades para resolver la desigualdad y definir el dominio, como lo demuestra la resolución del grupo G8:
representa el modelo obtenido, para determinar el dominio del modelo. Basados en los datos de la tabla se determinó los valores de Importar imagen por los que una solución tiene un pH de tipo ácido. El modelo logarítmico se traduce en una función estrictamente decreciente, lo que repercutirá en el orden de la desigualdad que traduce el enunciado. Los grupos que respondieron incorrectamente tuvieron dificultades para resolver la desigualdad y definir el dominio, como lo demuestra la resolución del grupo G8: 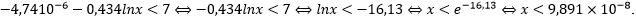
Al resolver esto usando la calculadora gráfica, hay varias limitaciones, a saber, la definición de la ventana de visualización. Al graficar el modelo logarítmico y la recta de ecuación 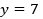 en una ventana de visualización adaptada a la situación de la tarea, es imposible observar la intersección de las dos curvas; dado que los valores son demasiado pequeños, incluso ampliando el gráfico es imposible ver la intersección. Estas limitaciones provienen de las limitadas capacidades tecnológicas de la calculadora gráfica para representar cantidades infinitamente pequeñas o grandes. El hecho de que la solución no pueda leerse gráficamente puede haber perturbado a los alumnos en el uso de la calculadora gráfica en este apartado.
en una ventana de visualización adaptada a la situación de la tarea, es imposible observar la intersección de las dos curvas; dado que los valores son demasiado pequeños, incluso ampliando el gráfico es imposible ver la intersección. Estas limitaciones provienen de las limitadas capacidades tecnológicas de la calculadora gráfica para representar cantidades infinitamente pequeñas o grandes. El hecho de que la solución no pueda leerse gráficamente puede haber perturbado a los alumnos en el uso de la calculadora gráfica en este apartado.
En cuanto al apartado 5, muy pocos grupos tuvieron tiempo de explorarlo. Solo dos grupos respondieron, identificando que una de las diferencias entre el modelo teórico de pH y el modelo obtenido a través de la tarea era la base del logaritmo, siendo un logaritmo decimal para el modelo teórico y un logaritmo neperiano para el modelo, como ilustra la respuesta del grupo G3: La fórmula estándar de pH se presenta a través del logaritmo decimal. En cambio, el modelo que presentamos se da en función del logaritmo neperiano. En la presentación a la clase de los resultados del grupo G3, se recordó el procedimiento para cambiar la base de los logaritmos a cualquier base  para trabajar con logaritmos de bases iguales. De esta manera, se puede comparar la exactitud del modelo obtenido con el modelo teórico del enunciado.
para trabajar con logaritmos de bases iguales. De esta manera, se puede comparar la exactitud del modelo obtenido con el modelo teórico del enunciado.
3.4. Actividades y dificultades experimentadas por los alumnos
Basándose en el estudio empírico de Stillman et al. (2007), la tabla 1 ilustra el rendimiento de estudiantes en la realización de actividades cognitivas clave para resolver convenientemente las tareas de modelado propuestas.
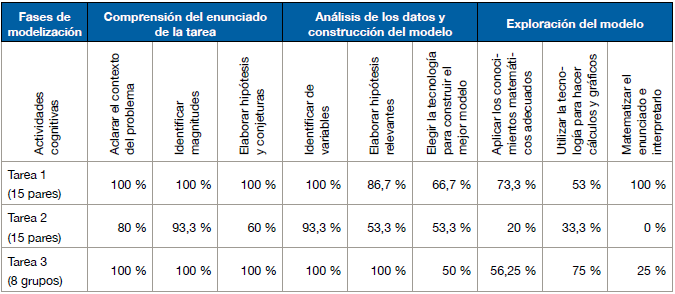
Tabla 1 Tasa de éxito de las actividades de estudiantes en la exploración de las tareas de modelización (%)
El análisis de la tabla muestra que todo el alumnado, de alguna manera, realizó las actividades cognitivas esperadas mientras exploraban las tareas. Se identifican algunas habilidades de modelado, matemáticas y tecnológicas, que fueron fundamentales para la exploración de la tarea y que están en línea con la literatura (Niss y Højgaard, 2019). Una de ellas es la interpretación del enunciado. Los alumnos, en su mayoría, identificaron, al leer el enunciado, la información relevante y la que no lo es, y las variables dependientes e independientes.
En la elaboración del modelo, fue primordial colocar y organizar los datos en la calculadora gráfica, saber trabajar con listas, representar la nube de puntos asociada a los datos y definir la lista que corresponde a cada variable. Los alumnos comprobaron qué modelo se ajustaba mejor a los puntos que representaban los datos en la tarea a partir de la nube de puntos. Cabe señalar que algunos alumnos revelaron dificultades para organizar los datos en una tabla de acuerdo con la situación de la tarea y para saber utilizar y leer las regresiones disponibles en la calculadora gráfica.
Para la exploración de las preguntas, era esencial aplicar los conocimientos matemáticos. A partir del enunciado, los alumnos tradujeron y relacionaron la información con el modelo obtenido. A medida que aumentaba la complejidad de las tareas, los alumnos mostraban dificultades para aplicar correctamente estos conocimientos matemáticos. Reconocer la necesidad de utilizar la calculadora gráfica para realizar cálculos, representar gráficos, resolver ecuaciones y comprobar resultados se hace inevitable al explorar este tipo de tareas. También se destaca la necesidad de que los alumnos sepan graficar una función y definir una ventana de visualización adecuada a la situación, aunque esto puede llevar a representaciones confusas cuando se trata de magnitudes desproporcionadas (Campos et al., 2015; Consciência, 2013). Sin embargo, sin una base teórica sólida, los alumnos no pueden identificar si lo que aparece en la pantalla de la calculadora gráfica es matemáticamente válido y si es coherente con la situación de la tarea (Conciencia, 2013).
4. Discusión y conclusiones
Para valorar las acciones de los alumnos, en una perspectiva de enseñanza exploratoria propicia para la exploración de las tareas de modelización (Blum y Borromeo Ferri, 2009; Borromeo Ferri et al., 2017; Ponte, 2005), la actividad del alumnado se realizó en pequeños grupos. Esta organización de los alumnos proporcionó las condiciones para que aprendieran a trabajar en grupo, desarrollaran la capacidad de comunicación matemática y la actitud de ser críticos con los resultados obtenidos (Rodríguez-García y Arias-Gago, 2020). Paulatinamente, la participación de los alumnos en las actividades realizadas en su grupo y en la clase, el grupo aumentó en la resolución de las tareas propuestas, lo que corrobora los resultados obtenidos por Blum y Borromeo Ferri (2009) y Sawalha (2018). Tal participación indica que se debe a la naturaleza de las tareas de modelización, que instigó a los y las estudiantes a compartir ideas y estrategias y a confrontar conocimientos, procesos y resultados.
La implementación de las tareas de modelización matemática se basó en el ciclo de modelización definido por Stillman et al. (2007), adaptando las fases de este ciclo a lo que se pretendía conseguir en las lecciones impartidas en el estudio de la función logarítmica. Con la ayuda de la calculadora gráfica, los alumnos realizaron las fases de comprensión del enunciado, análisis de los datos, construcción y validación del modelo y exploración del modelo. Estas fases permiten caracterizar la secuencia de actividades que realizan al explorar las tareas propuestas en el aprendizaje de los temas estudiados.
Después de leer las tareas propuestas, la mayoría del alumnado puede interpretar los respectivos enunciados, identificando las variables independientes y dependientes. Logran esta identificación debido al desarrollo de su razonamiento funcional, una habilidad que se espera desarrollar al final de los estudios de secundaria (Ambrus et al., 2018, Ministerio de Educación, 2017). Es una habilidad que permite al alumnado a establecer relaciones entre los datos que extraen de la interpretación de los enunciados de las tareas y entre los valores de las variables. La percepción del comportamiento de los valores de las variables se hace evidente cuando estos valores se organizan en tablas o gráficos de dispersión. El significado que se extrae de este análisis pone de manifiesto la relevancia de la conexión entre las diferentes representaciones matemáticas de los conceptos de función (Viseu et al., 2022). La representación numérica se articula con la representación simbólica (una expresión algebraica que traduce el modelo), que a su vez se articula con la representación gráfica.
Al construir el mejor modelo que se ajusta a los datos recogidos, los y las estudiantes dan sentido al modelo matemático que obtienen y a los procedimientos necesarios para realizar regresiones estadísticas en la calculadora gráfica. Se trata de un conocimiento de los esquemas de actuación instrumentados que se desarrollan al aprovechar este dispositivo tecnológico (Teixeira et al., 2016), que se traduce en la identificación de los roles de los parámetros que integran los diferentes modelos que proporciona la calculadora gráfica, el significado del valor del coeficiente de determinación y la definición de la ventana de visualización.
En cuanto a la exploración del modelo, el alumnado siguió diferentes estrategias de resolución, ya sea mediante procesos analíticos o con la ayuda de la calculadora gráfica. Al explorar este dispositivo tecnológico, el alumnado reveló inicialmente algunas limitaciones para integrarlo en sus actividades. Dichas limitaciones se deben a la falta de familiaridad con su uso, lo que repercute en la forma en que el profesor los guía: explorando el menú de estadística, editando expresiones algebraicas en el menú de edición de funciones y definiendo la ventana de visualización. Se percibe en este estudio que las tareas que no siempre permiten resolver con papel y lápiz empujan a los y las estudiantes a sentirse más familiarizados con la herramienta, lo que tiene implicaciones en el sentido conceptual que le dan a los temas en estudio.
La exploración del menú estadístico de la calculadora gráfica en la resolución de las tareas de modelización permite determinar el coeficiente de determinación, que informa de la razonabilidad o no del modelo encontrado para ajustarse a los datos que resultan de la tarea que se resuelve. El modelo determinado traduce la función que es objeto de estudio por parte del alumnado, que, en el caso de este trabajo, les dirigió a aprender la noción de logaritmo de un número en una base determinada, las funciones logarítmicas y sus propiedades, así como la derivada de una función logarítmica. Estos resultados concluyen que la resolución de las tareas de modelización se basa en la valorización de la comprensión conceptual de los temas objeto de estudio y de los procedimientos de cálculo necesarios para resolver un problema (Kenney y Kastberg, 2013). Se trata del desarrollo de habilidades intrínsecas a la resolución de tareas de modelización, entre las que se encuentran la comprensión de diferentes representaciones matemáticas, el sentido de la simbología matemática y la capacidad de comunicación matemática que, en el mundo actual, mucho se hace a través de dispositivos tecnológicos (Niss y Højgaard, 2019).
En cuanto a las dificultades que el alumnado manifestó tener en la resolución de las tareas de modelización, la interpretación del enunciado resultó ser un reto en la exploración del modelo, como señalan Stillman et al. (2007). Algunos estudiantes sintieron dificultad para conectar el contexto de la tarea con el modelo matemático obtenido, lo que se tradujo en una dificultad para dar sentido al modelo matemático con el que estaban trabajando, a las funciones en general y a sus propiedades.
En cuanto a la definición del mejor modelo que se ajusta a los datos del enunciado, el alumnado mostró poca familiaridad con el uso de las funciones de la calculadora gráfica para organizar los datos, representar nubes de puntos y preparar regresiones estadísticas. Es primordial que conozcan las características de la calculadora gráfica para poder organizar los datos en una tabla, graficar la nube de puntos asociada, construir un modelo matemático que se ajuste a la situación de la tarea y, en consecuencia, resolver este tipo de tareas (Blum, 2002; Campos et al., 2015). Este tipo de actividades se ven reforzadas por la resolución de tareas que animan a los y las estudiantes a recopilar y organizar datos y a modelar la situación problemática objeto de estudio desde una perspectiva funcional. Poco a poco, el alumnado se da cuenta de la utilidad de lo que aprenden en la escuela para comprender situaciones y resolver problemas que se encuentran a diario. Se trata de una perspectiva de enseñanza que promueve el diálogo entre dos mundos, el real y el matemático, muy distinta de la perspectiva que empuja a alumnos a reproducir hechos y procedimientos.
En la fase de exploración del modelo, algunos alumnos revelaron algunas dificultades en el uso de la calculadora gráfica para superar las limitaciones de los procesos analíticos específicos. La definición de la ventana de visualización dificultó a algunos estudiantes, ya que depende del dominio del modelo y del contexto de la situación de la tarea. Una ventana de visualización mal ajustada puede llevar a malinterpretar la representación gráfica y convertirse en un obstáculo en la exploración de este tipo de tareas (Arcavi, 2003; Viseu y Menezes, 2014). El uso adecuado de la calculadora gráfica implica intrínsecamente tener conocimientos matemáticos sólidos para relacionar los conceptos y propiedades de las funciones con su representación gráfica y recíprocamente (Consciência, 2013). Para disfrutar plenamente del potencial de la calculadora, es esencial conocer los conceptos matemáticos y comprender las notaciones que aparecen en la pantalla (Galbraith y Stillman, 2006).
En términos generales, se infiere con los resultados de este estudio que la resolución de tareas de modelización promueve en alumnos la adquisición de conocimientos (en este caso, de hechos y procedimientos de la función logarítmica) y el desarrollo de habilidades (razonamiento y resolución de problemas) y actitudes, incluyendo la autonomía, el pensamiento crítico y la búsqueda de profundización científica, técnica y tecnológica.
En la realización de este trabajo surgieron algunas limitaciones. Una de ellas se debió al uso de la calculadora gráfica. A pesar de que el alumnado tiene una calculadora gráfica desde el 10º grado, se constató que desconocían ciertas características de la calculadora gráfica, en particular la capacidad de organizar los datos y realizar regresiones estadísticas a partir de esos datos. Definir una ventana de visualización que se adapte a la representación gráfica o a una parte de ella, dependiendo de los objetivos de la tarea, resultó ser un reto para el alumnado. Sin una ventana de visualización adecuada, se pueden extraer conclusiones erróneas sobre las características de la función considerada a partir de la lectura e interpretación de la pantalla de la calculadora gráfica. Además, los modelos logarítmicos establecen relaciones entre magnitudes que a menudo no son razonables en la representación gráfica. Debido a las limitaciones tecnológicas de la calculadora gráfica, en concreto la resolución de la pantalla (384×216 píxeles), esta no puede representar partes concretas de la gráfica de las funciones subyacentes a estos modelos.
En consecuencia, la lectura e interpretación de la representación gráfica obtenida con la calculadora, así como la resolución gráfica del problema, se ven perturbadas. Otra limitación estaba relacionada con el diseño de las tareas que implicaban modelos logarítmicos. Fue un gran reto proponer tareas de modelización que se ajustaran a los objetivos de aprendizaje planteados en el plan de estudios y que estuvieran asociadas a fenómenos naturales significativos. En particular, el diseño de tareas de modelización de contexto real, centradas en las propiedades de la situación problema y no semi-real, centradas únicamente en sus propiedades matemáticas (Ponte y Lent, 2012), resultó ser una tarea ardua de realizar. Dicha limitación pone de manifiesto la integración de las tareas de modelización en las estrategias de enseñanza en la formación de los futuros profesores de matemáticas, promoviendo el desarrollo de su conocimiento profesional sobre las características de las tareas que los actuales programas de enseñanza de las matemáticas recomiendan integrar en las estrategias de enseñanza.