Forma sugerida de citar:
Vanegas, Y., Prat, M. y Edo, M. (2022). Representaciones matemáticas de niños y niñas de 5-6 años cuando resuelven un problema abierto. Alteridad, (17) 2, 180-193. https://doi.org/10.17163/alt.v17n2.2022.02
1. Introducción y estado de la cuestión
Los planteamientos curriculares actuales para la educación infantil remarcan la importancia de los enfoques globalizados, la interdisciplinariedad y la necesidad del desarrollo de competencias (National Council of Teachers of Mathematics-NCTM, 2000; 2014; Ministerio de Educación y Formación Profesional, 2022; National Association for the Education of Young Children-NAEYC, 2020). Autores como Clements y Sarama (2016); De Castro et al. (2012); Vanegas y Giménez (2018) entre otros, resaltan el papel de los procesos matemáticos en la adquisición de competencias y señalan que estos son fundamentales para promover la capacidad de usar de forma comprensiva y eficaz las matemáticas que se aprenden en la escuela en una variedad de contextos. Apoyar y enriquecer estos procesos y promover el desarrollo del pensamiento matemático de los niños y las niñas es uno de los desafíos de la educación infantil (Baroody, 2003; Cheeseman, 2019; Clements y Sarama, 2021; Ginsburg y Amit, 2008: Lopes et al., 2017). En consecuencia, plantear y resolver problemas, analizar diferentes estrategias y soluciones, y, reflexionar sobre estas deben ser actividades centrales en los procesos de enseñanza y aprendizaje de las matemáticas en cada uno de los niveles escolares (NAEYC y NCTM, 2013; Mason, 2016; Schoenfeld, 2016).
De acuerdo con Edo (2005), el aprendizaje de las matemáticas es un proceso de construcción socialmente mediado. Y, esto es especialmente relevante cuando se piensa en la educación infantil, ya que implica, asumir que niños y niñas no aprenden recibiendo y acumulando pasivamente información del entorno, sino que lo hacen a través de un proceso activo de elaboración de significados y de atribución de sentidos donde la resolución de problemas, la comunicación y la representación son procesos fundamentales (Battista, 2016). Si se consideran las matemáticas como el resultado de ciertas acciones desarrolladas por las personas y como un fenómeno cambiante, la actividad matemática debe caracterizarse por el deseo de hallar algo: unos datos, unos procesos, unas relaciones, unos resultados, una forma de comunicar, etc. Por tanto, la educación matemática en las primeras edades debería centrarse en ayudar a los niños a vivir situaciones de actividad matemática, es decir, situaciones de búsqueda donde el eje central sean las prácticas realizadas por los niños.
Como lo plantean Baroody (1993), Saundry y Nicole (2006) y Carruthers y Worthington (2010), las representaciones y el dibujo son una herramienta fundamental para la resolución de problemas en las primeras edades. Estos autores argumentan que las representaciones son esenciales en la construcción de significados. Ya que las representaciones ayudan a los niños a concretar los problemas y decidir el procedimiento a utilizar en su resolución. Carruthers y Worthington (2009) además remarcan la importancia que el profesorado reconozca las representaciones realizadas por los niños mientras resuelven problemas. De esta forma podrán identificar mejor las ideas y formas de razonar de los niños. Por ello, consideramos pertinente explorar el tipo de representaciones y la manera cómo niños de educación infantil resuelven problemas. Concretamente, el propósito de este artículo es describir el tipo de representaciones y estrategias utilizadas por un grupo de niños de edades iniciales (5-6 años) cuando se involucran en una tarea de resolución de un problema abierto.
Este estudio se sustenta en dos grandes ejes. El primero referido a la resolución de problemas abiertos en edades tempranas y el segundo relacionado con el uso de las representaciones y su importancia en la resolución y comunicación de problemas.
Ramírez y de Castro (2014) plantean que es fundamental introducir la resolución de problemas en la educación infantil ya que no solo estimula el desarrollo de estrategias informales sino porque ayuda a que los niños y las niñas doten de significado las operaciones aritméticas y den sentido a ciertos procedimientos que aprenderán cuando avancen en su escolaridad. Coincidimos con Alsina (2012) quien siguiendo los planteamientos del NCTM (2000) plantea que hay cuatro aspectos referentes a la resolución de problemas que se deberían trabajar desde la educación infantil: a) construir el conocimiento matemático por medio de la resolución de problemas, plantear una variedad de contextos; b) resolver problemas que surgen de las matemáticas y en diferentes contextos, situaciones de vida cotidiana, rutinas diarias, situaciones de experimentación, entre otras; c) aplicar y adaptar una variedad de estrategias apropiadas para resolver problemas, como por ejemplo plantear buenas preguntas; fomentar la interacción, la negociación y el diálogo en el aula; etc.; y, d) regular y reflexionar sobre el proceso de resolver problemas matemáticos.
Si bien es cierto que hay diversos tipos de problemas matemáticos (realistas, auténticos, abiertos, entre otros), son los docentes quienes eligen usar unos u otros en función de los objetivos que se proponen en su práctica docente. Según Pehkonen (1997) un problema abierto es aquel donde la situación de partida o la de llegada son abiertas, en contraposición a los problemas cerrados donde el inicio y el final están exactamente explicitados. En este grupo se encuentra Baroody (1988) quien distingue entre problemas de enunciado verbal rutinarios y no rutinarios. Los problemas no rutinarios son aquellos que implican diversos procedimientos para su resolución, y pueden tener diversas respuestas. Dentro de los problemas rutinarios o no rutinarios, se encuentran los de repartición; los cuales implican la acción de separar en unidades o en conjunto, el total de las partes. En la investigación de Saundry y Nicole (2006) se plantean dos tipos de problemas de repartición no rutinarios: a) Problemas aritméticos de repartición que parten de una agrupación (conjunto de elementos), que luego deberá ser repartida; y, b) Problemas aritméticos de repartición que también parten de una agrupación (conjunto de elementos), pero donde su repartición implica más de una operación para resolverlo (un conjunto de elementos debe ser repartido en subconjuntos).
En las primeras edades las representaciones sirven tanto para construir conocimientos matemáticos nuevos como para expresar ideas matemáticas (NCTM, 2000). En este sentido, Burgués y Sarramona (2013) afirman que es deseable que el lenguaje matemático se convierta en una forma natural de expresión dentro de la clase entre los docentes y los niños. Para lograr este objetivo se debe potenciar la conversación sobre las matemáticas, primero mediante el lenguaje verbal, y de forma progresiva ir introduciendo los términos y formas propias del lenguaje matemático (de forma oral y escrita). No se trata de que los niños memoricen símbolos, sino de que aprendan a comunicar sus ideas matemáticas con sentido, por ello la importancia de explorar sus representaciones.
Los docentes deben, en su tarea de enseñanza, analizar tanto las representaciones de sus alumnos como sus discusiones (su comunicación matemática) para poder evaluar el desarrollo de su pensamiento matemático y así poder ofrecerles los elementos necesarios para que puedan conectar sus propios lenguajes al lenguaje matemático convencional (NCTM, 2000; Edo et al., 2009). Lo cierto es que los niños de manera natural representan ideas cognitivas a través del papel, los objetos, el juego, etc., en definitiva, utilizan las representaciones para plasmar sus esquemas y dotarlos de sentido en el papel (Carruthers y Worthington, 2006; Worthington, 2009).
Son diversos los autores que han estudiado las representaciones matemáticas de los niños en las primeras edades. Así, Deliyianni et al. (2009) estudiaron los modos de representación generados por el alumnado de educación infantil y primaria examinando el cumplimiento de las normas durante el contrato didáctico en la solución de problemas. Mientras que Nicol y Saundry (2006) investigaron cómo niños de las primeras edades piensan matemáticamente y representan un problema aritmético. Smith (2003) y Woleck (2001) afirman que los dibujos cumplen dos funciones fundamentales: a) sirven para modelizar los problemas y b) son el soporte de la actividad matemática que permite resolverlos. Además, señalan la importancia de escuchar las explicaciones del alumnado sobre sus dibujos para comprender la actividad matemática que realizan. En el caso de Carruthers y Worthington (2006), a partir del análisis de dibujos y escritos matemáticos elaborados por niños hasta los ocho años, identifican cinco tipos de gráficos: dinámico, pictográfico, icónico, simbólico y escrito. Para Carruthers y Worthington (2005, 2006), los niños alcanzan el significado matemático de los símbolos abstractos, a partir de sus propias representaciones y construyendo su propio significado.
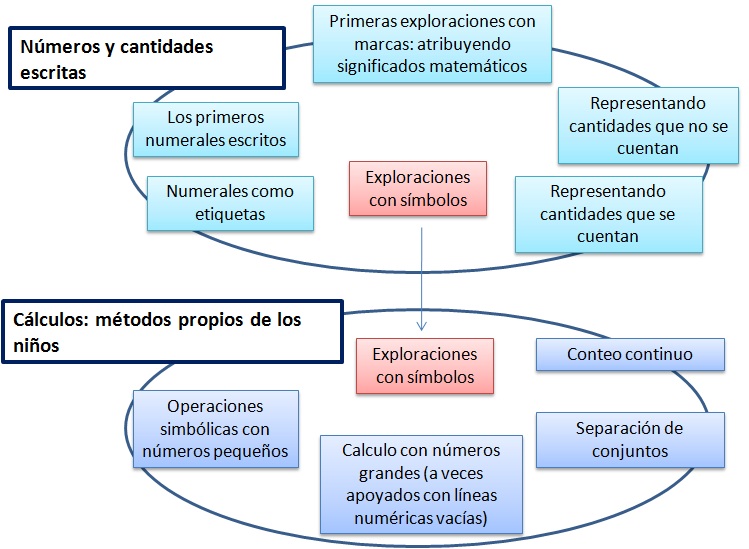
Carruthers y Worthington (2006) proponen dos dimensiones para interpretar los gráficos matemáticos de niños y niñas de 0 a 8 años. La primera referida a las representaciones escritas de los números y las cantidades y la segunda centrada en los métodos de cálculo escrito ideados por los niños. Estas autoras, también elaboran una taxonomía no jerárquica (figura 1) en la que se ilustran las categorías consideradas en cada una de las dimensiones señaladas para la caracterización de los gráficos matemáticos de los niños (Carruthers y Worthington, 2013).
Nota. Carruthers y Worthington (2013).
Figura 1 Traducción Taxonomía: gráficos matemáticos de los niños
En la primera dimensión: representaciones escritas de números y cantidades se consideran cinco categorías:
Primeras exploraciones con ‘marcas’ a veces estas primeras representaciones son vistas por los adultos como simples garabatos, pero significan un paso importante para los niños en su camino hacia las representaciones multidimensionales de su mundo.
Primeros numerales escritos o cuando los niños se refieren a sus marcas como números. En este momento los niños entienden que números y letras tienen significado y empiezan a hacer una diferenciación general entre ellos: “esto es un número”, aunque sean marcas aún no reconocibles como números, pero pueden tener cualidades numéricas.
Numerales como etiquetas, en este caso los niños identifican en su entorno números y letras, y muestran interés por usarlos; observan la función de los números escritos en un sentido social. Hay un momento en el cual los niños pasan de identificar estos símbolos en su entorno a escribirlos para sus propios fines. Este es un cambio significativo ya que, al elegir escribir estos números, convierten lo que leyeron en un lenguaje simbólico estándar y eligen usarlos en contextos significativos.
Cantidades representadas que no se cuentan, se trata de las representaciones elaboradas por los niños más pequeños, representaciones vivas y que no son demasiado exactas. Por ejemplo, el caso de un niño de tres años, que representa una araña de ocho patas, pero la representación muestra una araña con muchas patas, más de ocho. Está claro que el niño representa su sentido personal de cantidad no una cantidad concreta.
Cantidades representadas que se cuentan, en este caso los niños hacen representaciones de cantidades y las cuentan, por ejemplo, dibujando un cierto número de líneas verticales y diciendo que son “gotas de lluvia” y contándolas al terminar. Para Carruthers y Worthington (2010), las cantidades que no se cuentan preceden a las que se cuentan, pero puede suceder que haya una superposición de estos dos aspectos. A su vez, este aspecto del desarrollo lleva a los niños directamente al comienzo de los cálculos escritos.
Según Carruthers y Worthington (2006), a medida que los niños exploran los cálculos de diversas maneras, sus propias representaciones respaldan sus métodos mentales y los ayudan a calcular. El conteo tiene una fuerte presencia en los inicios del cálculo escrito (Clements y Sarama, 2013; Baroody et al., 2019)
En la segunda dimensión: métodos de cálculo ideados por los niños, se describen las siguientes categorías:
Conteo continuo, se refiere a las primeras representaciones que realizan los niños para la suma y la resta. Son diversos los estudios que demuestran que los niños pequeños realizan sumas y restas simples con estrategias de conteo, contándolo todo, todos los elementos. Así, si hay dos conjuntos, cuentan uno y cuando acaban siguen con el siguiente, sin que parezca que separan los dos conjuntos.
Separación de conjuntos, en este caso los niños exhiben diferentes estrategias para mostrar que dos cantidades están separadas. Realizan agrupaciones de dos o más conjuntos de elementos que deben sumarse, ubicando cada uno en un lado de la hoja de papel o dejando un espacio entre ellos; separando los conjuntos con palabras; poniendo una línea vertical entre los conjuntos, entre otras.
Exploración de símbolos, en este caso los niños comienzan a hacer uso explícito de los símbolos (inventados o en ocasiones utilizando símbolos estándar). También se considera cuando los niños hacen marcas en sus procedimientos que muestran que entienden los símbolos, aunque estos no aparezcan de manera explícita.
Operaciones simbólicas con números pequeños, en este punto los niños ya conocen los símbolos estándar, entendiendo su papel y han desarrollado estrategias para usar de manera flexible para resolver problemas.
Cálculos con números grandes (a veces utilizando anotaciones o líneas numéricas vacías). Calcular con números grandes es más difícil, ya que se necesita entender cómo son los números grandes involucrados y pueden necesitar manipular varios pasos. Aquí es donde los métodos mentales y algunos soportes enseñados pueden ser valiosos, como la línea numérica.
Cabe mencionar que las respuestas de los niños a determinada tarea matemática que implica la producción de representaciones pueden clasificarse en varias de estas categorías, no necesariamente en una exclusivamente.
Muchas veces ha surgido el cuestionamiento sobre cómo pueden resolver problemas matemáticos los niños muy pequeños, dado que, en su mayoría, no saben leer ni escribir. Este tipo de pregunta revela una idea errónea, que hay que superar (Lopes et al., 2017). Es importante entender que el pensamiento y el lenguaje están vinculados, y que precisamente las representaciones juegan un papel fundamental en las formas de razonamiento y comunicación de los niños. Investigar cómo responden los niños cuando se les presenta un problema matemático; los tipos de dibujos que hacen espontáneamente; las cosas que piensan mientras dibujan; las relaciones que establecen y expresan tanto de forma oral como escrita es clave para comprender la manera como construyen sus ideas matemáticas.
2. Metodología
En esta investigación usamos una metodología descriptiva-interpretativa (Latorre et al., 2003, Cohen et al., 2018). Se realiza un análisis descriptivo de los datos, para posteriormente relacionar e interpretar estas descripciones teniendo en cuenta los referentes teóricos considerados. Concretamente, se propone una tarea matemática con la que se pretende explorar y describir aspectos del pensamiento matemático de los niños participantes cuando resuelven problemas.
Para desarrollar el objetivo del estudio, se seleccionó un problema aritmético abierto. Dicho problema se implementó a un grupo de 23 alumnos de educación infantil (5-6 años) en una escuela de Cerdanyola del Vallès (Cataluña). El problema fue resuelto por los niños de manera individual y de forma escrita. Adicionalmente, para reconocer las estrategias y procesos seguidos por los niños en la resolución del problema se realizó una entrevista semiestructurada, la cual se registró en video.
El problema, es una adaptación del planteado por López (2015), donde se propone un contexto familiar a los niños, relacionado con la alimentación. A continuación, se presenta el enunciado del problema:
Quieres hacer una macedonia. Puedes comprar plátanos, peras, naranjas y manzanas. En total compras 15 piezas de fruta. Explica cuántas piezas compras de cada fruta.
En la elección y adaptación del problema se consideraron diversos aspectos, como los que señala Baroody (1993) cuando caracteriza los problemas no rutinarios: la incógnita no es evidente, el problema da información sobre el total de frutas, pero la incógnita hace referencia a la cantidad de frutas de cada tipo que se podrían tener para elaborar una macedonia con ese total. Se puede resolver de diferentes maneras y es posible obtener diversas soluciones.
El problema se presentó a los niños de forma oral y se dieron las siguientes consignas:
El problema debe resolverse individualmente.
Se pueden utilizar diferentes representaciones: dibujos, números, letras o varias de ellas al mismo tiempo.
Se deben utilizar mínimo dos tipos de fruta para responder al problema, pero no es obligatorio utilizar los cuatro tipos.
Se debe tener presente que se quieren utilizar 15 piezas de fruta.
Los niños disponían de hojas de papel en blanco para realizar sus propuestas. Según Edo y Marín (2017) es importante en el momento de plantear una propuesta de papel en blanco seleccionar convenientemente la consigna para que la representación gráfica que haga el niño muestre qué piensa y cómo razona. A su vez, es conveniente crear un clima de confianza y tranquilidad para que cada niño pueda reflexionar, escoger, representar y explicar su razonamiento. Las marcas del papel en blanco mostraran lenguajes y significados, permitiendo que el maestro pueda observar los aprendizajes de cada estudiante y así dar relevancia a las marcas del alumnado (Carruthers y Worthington, 2006).
Respecto a la entrevista semiestructurada, se establecieron una serie de preguntas base:
¿Me explicas qué has hecho?
¿Cuántas frutas has dibujado de cada tipo? ¿Por qué?
¿Estás seguro/a que tienes 15 frutas? ¿Cómo lo sabes?
¿Has dibujado todos los tipos de fruta? ¿Por qué?
¿Qué has hecho para saber cuándo debías parar de dibujar?
¿Has intentado poner el mismo número de cada tipo de fruta?
¿Qué indican los números que has escrito?
¿Cómo sabías cuántas frutas más debías dibujar mientras resolvías el problema?
Los datos de esta investigación son los protocolos escritos de cada uno de los participantes a la tarea propuesta y las transcripciones de los diálogos generados en las entrevistas. Esta información se organiza inicialmente en un instrumento de recogida de datos. A manera de ejemplo, en el Figura 2, se muestra un extracto de dicho instrumento. En este se incluye, el identificador asignado al alumno (A1), su respuesta escrita y la parte inicial de la entrevista.
El análisis de los datos se realizó en dos fases. En la primera fase se analizaron individualmente las respuestas de los niños al problema planteado, focalizando dicho análisis en las representaciones. Siguiendo la propuesta de Carruthers y Worthington (2005), se clasifican las representaciones en tres categorías: icónica, escrita y simbólica. No se consideran las dos categorías iniciales (dinámica y pictórica), propuestas por estas autoras, debido a la edad de los niños participantes en el estudio. En la tabla 1, se describen los indicadores asociados a cada una de estas categorías
En la segunda fase para complementar el estudio de las producciones de los niños se analizaron los métodos de cálculo que siguieron al solucionar el problema. Para este análisis, continuando con la taxonomía de caracterización de los gráficos matemáticos de niños planteada por Carruthers y Worthington (2013), se consideraron las categorías de la dimensión métodos de cálculos escritos: conteo continuo, separación de conjuntos, exploración de símbolos y cálculos con símbolos estándar de números pequeños. No se considera la categoría cálculo con números grandes, ya que no se adecua a las condiciones del problema.
Consideramos como Badillo et al. (2014) que las estrategias de resolución y las representaciones planteadas por los niños se conectan y, por tanto, una mirada global permitirá hacer un análisis más rico de las prácticas matemáticas desarrolladas por los niños al resolver el problema. Se construye un instrumento de análisis donde se combinan los aspectos analizados en las fases 1 y 2. A continuación, en la figura 3 ejemplificamos el análisis realizado de la respuesta dada por el alumno diez (A10).
3. Resultados
Los resultados se organizan en dos partes: caracterización de las representaciones utilizadas por los niños e identificación de las estrategias desarrolladas en la resolución del problema.
3.1 Caracterización de las representaciones utilizadas por los niños
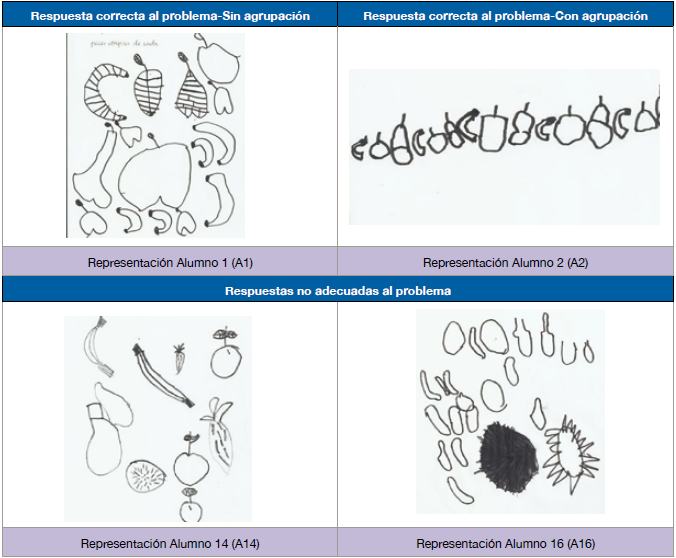
En cuanto al tipo de representaciones encontramos que los 23 alumnos que participan en el estudio utilizan representaciones icónicas. Al usar este tipo de representación los niños se apoyan en el dibujo para realizar el conteo y controlar la cantidad total definida en el problema propuesto. Sus dibujos indican a la vez, el tipo de frutas elegidas por los niños, la cantidad que han considerado para cada tipo y en algunos casos la intencionalidad de hacer agrupaciones (reparticiones). Cabe mencionar que, aunque todos proponen una representación icónica no todos resuelven de manera adecuada el problema, es el caso de cinco de los niños. En la figura 4 se muestran diferentes ejemplos de respuestas, donde se evidencian los aspectos antes señalados.
Del total de niños, tres, además de usar una representación icónica también utilizan una representación simbólica. En estas representaciones se evidencia un razonamiento más complejo. Los niños que realizaron representaciones icónicas-simbólicas ya no se centran solo en el conteo para llegar al total, sino en lo operativo, proponiendo diferentes subgrupos para cumplir con la condición de tener 15 frutas en la macedonia. Estas representaciones incluyen, además del dibujo de las frutas que cada niño ha considerado, los numerales que indican la cantidad que han asociado a cada tipo (ver figura 5).
A continuación, en la figura 5 se presenta un ejemplo de respuesta en el que se combinan representaciones. En las representaciones propuestas por A4 y A12, se puede constatar que los niños reconocen que el todo (15 frutas) se puede separar en conjuntos discretos de varios elementos (p. ej. plátanos, naranjas, manzanas y peras), que pueden tener (o no) diferente cardinal (p. ej. 5, 4, 3, 3 o 5, 4, 3, 2, 1).
3.2 Identificación de métodos de cálculo desarrollados en la resolución del problema
En cuanto a los métodos utilizados por los niños para resolver el problema según las dimensiones planteadas por Carruthers y Worthington (2006) se observó que 19 de las propuestas de solución de los niños se clasifican en la categoría conteo continuo y cuatro en la de separación de conjuntos. En el primer caso se clasifican aquellas representaciones que expresan una cantidad. Los niños representan y cuentan cosas que eligen (en este caso frutas) pero que no ven físicamente (p. ej. A1, ver figura 4). Normalmente este tipo de representaciones se dibujan en una disposición lineal horizontal (p. ej. A2, ver figura 4), aunque se pueden encontrar otras disposiciones. Se considera que es el primer paso para la exploración del cálculo. En nuestro caso la mayoría de los niños se centraron más, en el objetivo de tener 15 piezas de fruta, que en el orden al elegir qué tipo fruta dibujar. Si nos fijamos en la solución dada por A10 (figura 3) el número final de su recuento representa el total. Estas diferentes prácticas matemáticas relativas al conteo continuo son clave para reconocer las estrategias que los niños están desarrollando al sumar (Carruthers y Worthington, 2006). Así, algunos niños, como se constató en las entrevistas, contaban continuamente, empezando por una de las frutas, la que ellos consideraban “la primera”. Casi todos los niños entienden que es necesario contar todo para llegar a un total, excepto aquellos que no lograron resolver de forma adecuada el problema (p. ej. A14, A16-figura 4).
En el segundo caso las representaciones indican separaciones en subgrupos de frutas (p. ej. A2 - figura 4, A4 y A12 - figura 5). En nuestro estudio, ninguno de los niños utilizó marcas (líneas, palabras, círculos, etc.) para diferenciar los subgrupos. Pero en los cuatro casos ubicados en esta categoría los niños representan conjuntos separados (de frutas) que luego suman para cumplir con la condición de tener 15 piezas en total en la macedonia. El alumno A2 (figura 4) utiliza el espacio y la distribución de las frutas para indicar las sub-agrupaciones que ha realizado de las frutas. En la entrevista se corrobora que ha realizado grupos de plátano-manzana-pera. Identificando tanto el conjunto como los elementos del conjunto y repitiéndolo continuamente hasta llegar a 15. En el caso de A4 (figura 5), a partir de la entrevista se pudo constatar que realiza el cálculo como una narración en palabras (Carruthers y Worthington, 2006) cuando describe lo que ha realizado: “Aquí he sumado cinco plátanos y cuatro naranjas y después he sumado tres manzanas y tres peras para que me saliera 15”.
Finalmente, encontramos tres soluciones que se ubican en la dimensión: exploración de símbolos. Según Carruthers y Worthington (2006) los niños ubicados en esta categoría organizan sus soluciones y las representan a veces dejando un espacio entre los conjuntos para implicar que un (operante) es necesario en dicho lugar, por ejemplo, como ocurre en la solución dada por A4 (figura 5). Usualmente utilizan símbolos personales o inventados, o aproximaciones de los símbolos estándar. En nuestro estudio, los tres niños utilizan los símbolos estándar de los numerales para indicar la cantidad que ellos asocian a cada tipo de fruta o para apoyar el conteo continuo (A10-figura 3). En otro caso uno de los niños (A12-figura 5) hace uso de la palabra “y” para indicar “+”. También es característico de esta categoría la combinación de dibujos, palabras, números y/o símbolos personales, como ocurre en los tres casos aludidos.
Los niños que realizan representaciones que combinan lo icónico y simbólico, son aquellos que también utilizan estrategias de exploración de símbolos, evidenciando un razonamiento más complejo. Pasar a otro tipo de estrategias, como la realización de operaciones simbólicas estándar con números pequeños, requiere que los niños las hayan desarrollado previamente. Aunque cabe precisar, como plantean Vanegas y Giménez (2018) que cuando los niños resuelven problemas lo importante no es el paso de una estrategia a otra sino el uso de estrategias apropiadas que muestran una interpretación cada vez más completa y adecuada del problema.
Discusión y conclusiones
Consideramos, como plantean Carruthers y Worthington (2005), que a veces los niños utilizan una combinación de representaciones, por ejemplo, icónica y simbólica, cuando están en un período de transición. Parece que cuando lo hacen están pasando de representaciones que les son conocidas a otras nuevas, aunque todavía no están preparados para prescindir de elementos no esenciales. En nuestro estudio esto ocurre con tres de los 23 participantes. Este período de transición es muy importante a medida que los niños avanzan hacia formas más abstractas de las matemáticas. Sin embargo, también es importante tener en cuenta que algunos niños vuelven a formas gráficas menos desarrolladas cuando encuentran que las matemáticas que se presentan son más desafiantes, ya que se basan en conocimientos previos y en formas con las que se sienten más seguros.
Cuando los niños pasan de reconocer los números como símbolos asociados a diferentes contextos de su vida y pasan a escribirlos con fines propios y concretos, es evidencia de un cambio significativo, ya que cuando eligen escribir determinados números (en nuestro estudio, para indicar el total de frutas de cada tipo que utilizarían para hacer la macedonia) han convertido lo que leen en un lenguaje simbólico estándar y han elegido utilizarlos en contextos significativos (Worthington y van Oers, 2017). Es importante involucrar a los niños en ambientes de juego y resolución de problemas que les desafíen y que permitan experimentar y elegir sus propios métodos.
El reconocimiento de las diferentes representaciones utilizadas por los niños cuando enfrentan tareas matemáticas permitirá a los maestros reconocer mejor sus formas de razonamiento y los aspectos a los que dan relevancia cuando trabajan determinadas nociones matemáticas. Además, el análisis de las representaciones y las estrategias asociadas permitirá al docente evaluar de forma más idónea el desarrollo del pensamiento matemático de los niños. En consecuencia, se podrán diseñar nuevas tareas escolares que ayuden a los niños a desarrollar habilidades para explicar, describir, relacionar y argumentar.
La riqueza de los problemas y/o tareas que se propone a los niños es un elemento clave para potenciar el desarrollo de su pensamiento matemático. En efecto, los problemas deben ser planteados en una amplia gama de contextos que tengan un significado real para los niños, esto les ayudará a dar un sentido personal a las matemáticas. Consideramos, como plantean NAECY & NCTM (2013), que la resolución de problemas, el razonamiento, la comunicación, las conexiones y la representación hacen posible que los niños adquieran el conocimiento del contenido. Estos procesos se desarrollan a lo largo del tiempo si se apoyan en oportunidades de aprendizaje bien diseñadas. El desarrollo y el uso de estos procesos por parte de los niños es uno de los logros más duraderos e importantes de la educación matemática. Sus ideas intuitivas se convierten en verdaderas matemáticas cuando los niños reflexionan sobre ellas, las representan de diversas maneras y las conectan con otras ideas.
A partir de nuestra investigación hemos podido mostrar cómo el análisis de las representaciones y estrategias de los niños en un ambiente de resolución de problemas puede proporcionarnos una importante retroalimentación sobre el pensamiento de los niños, por ende, nos brinda elementos relevantes para la reflexión que debe hacerse sobre este tema en la formación inicial de docentes de educación infantil. Esperamos seguir trabajando en esta línea, por un lado, explorando las representaciones que los niños construyen cuando se involucran en diferentes tareas matemáticas por otro, analizando y utilizando diferentes referentes para caracterizar dichas representaciones e incorporar estos hallazgos en tareas profesionales en la formación inicial de profesores. Nos interesa que los futuros docentes reconozcan que es posible desarrollar unas matemáticas de calidad desde las edades iniciales (Lee y Ginsburg, 2007) y que identifiquen cómo los resultados de investigaciones como la descrita en este artículo pueden ser útiles en su contexto profesional apoyando el diseño, planificación y evaluación de propuestas escolares que promueven el desarrollo del pensamiento matemático en la educación infantil.