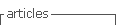Forma sugerida de citar:
Acosta-Inchaustegui, Y. y Alsina, Á. (2022). Influencia del contexto de enseñanza en la representación de patrones en educación infantil. Alteridad, (17)2, 166-179. https://doi.org/10.17163/alt.v17n2.2022.01
1. Introducción y estado de la cuestión
En los últimos años, se le ha conferido a la infancia una especial importancia para el desarrollo integral de la persona. Bowman et al. (2001, p. 23), por ejemplo, afirman que “[…] los niños pequeños son estudiantes capaces y que la experiencia educativa durante los años preescolares puede tener un impacto positivo en el aprendizaje escolar”. En este sentido, diversas investigaciones señalan que las competencias matemáticas tempranas (de 4 a 6 años básicamente) pueden llegar a ser un indicador del éxito académico en etapas posteriores (Nguyen et al., 2016; Rittle-Johnson et al., 2017; Wijns et al., 2021, entre otros). En consecuencia, resulta necesaria una planificación e implementación efectiva que permita promover el desarrollo de la competencia matemática desde las primeras edades, diversificando el uso de escenarios educativos que conduzcan a buenas prácticas en el aula de matemáticas (Alsina, 2019, National Council of Teachers of Mathematics [NCTM], 2000, 2014).
Desde este prisma, este artículo asume el Enfoque de los Itinerarios de Enseñanza de las Matemáticas de Alsina (2019, 2020), en adelante EIEM, que plantea que la enseñanza de las matemáticas en las primeras edades debería proponerse como un recorrido de lo concreto a lo abstracto a través de secuencias de enseñanza que contemplen distintos contextos de enseñanza, con el fin de promover una adquisición consolidada de competencias matemáticas. Este enfoque establece una secuencia intencionada que incluye tres niveles de enseñanza que avanzan de lo particular a lo general, ofreciendo una orientación de uso jerarquizado de los contextos que lo conforman. En el primer nivel se encuentran los contextos informales que se deberían “consumir” diariamente: las situaciones reales, los recursos manipulativos y el uso de propuestas lúdicas y recreativas; en el siguiente nivel se hace alusión a los contextos intermedios que deberían utilizarse algunas veces, como los recursos literarios y tecnológicos; y finalmente, aparecen aquellos contextos formales que deberían implementarse ocasionalmente, como las fichas y los libros de texto.
En concreto, este artículo aplica este enfoque en la enseñanza de patrones de repetición, dado que se ha evidenciado que el conocimiento de patrones y su estructura influye positivamente en el desarrollo temprano del pensamiento matemático (Clements y Sarama, 2015; Lüken y Kampmann, 2018; Mulligan et al., 2020; Papic et al., 2011; Rittle-Johnson et al., 2018; Tirosh et al., 2018; y Wijns et al., 2021). Por lo tanto, la exploración de patrones puede considerarse una puerta de entrada para promocionar la generalización (Vanluydt et al., 2021), la anticipación, la conjetura, la justificación, la representación y el uso preciso del lenguaje matemático (Acosta y Alsina, 2020). Al hablar de patrones matemáticos, es necesario distinguir entre patrón como una secuencia o seriación ordenada, y entre estructura de patrón, es decir, organización o regla que subyace al patrón (Mulligan y Mitchelmore, 2009). Estas autoras australianas puntualizan que los patrones comprenden dos componentes: uno cognitivo, relacionado con el conocimiento de la estructura; y otro meta-cognitivo, asociado con la capacidad de búsqueda y análisis de patrones. Mulligan et al. (2020) exponen que la falta de consciencia del patrón y su estructura puede llegar a ser un predictor de dificultades matemáticas futuras. Sin embargo, poco se sabe sobre cómo influye el contexto de enseñanza en la comprensión y representación de patrones. De hecho, autores como Wijns et al. (2019) plantean la necesidad de estudiar si las tareas con patrones que se implementan promueven de forma óptima todo su potencial, para así fomentar el desarrollo de la percepción algebraica de los escolares. Como afirma Alsina (2020), el libro de texto se postula en ocasiones como un recurso preponderante que no deja espacio para abordar conceptos y procedimientos matemáticos desde otros escenarios más realistas, concretos y significativos para los escolares.
En esta línea, nuestro propósito es aportar datos que permitan iniciar una aproximación al modo en que los niños y niñas de 4 a 6 años ejecutan patrones de repetición y exteriorizan su representación en diversos contextos de enseñanza, para así abordar el desarrollo de la comprensión de patrones de una manera contextualizada y longitudinal, considerando los planteamientos del EIEM.
Desde esta perspectiva nos formulamos las siguientes preguntas de investigación:
¿Cómo influye el contexto de enseñanza en las tareas con patrones de repetición?
¿Qué relación se establece entre los contextos de enseñanza concretos (situaciones reales) y los contextos de enseñanza abstractos (recursos gráficos) durante la comprensión y representación de patrones de repetición?
De estas preguntas se derivan los siguientes objetivos de estudio:
Analizar la relación que se establece entre la comprensión y la representación de patrones de repetición.
Evidenciar la influencia que ejerce el contexto de aprendizaje en el éxito de la representación de patrones de repetición.
1.1. Enseñanza y representación de patrones de repetición desde el enfoque de itinerarios didácticos
En las siguientes líneas se abordan los pilares que fundamentan el EIEM como marco teórico de nuestro estudio, se define qué se entiende por patrón, la importancia de su enseñanza y la representación como proceso matemático que promueve la comprensión.
Acosta y Alsina (2021) señalan que el aprendizaje de los patrones se inicia en situaciones concretas hasta consolidarse en experiencias abstractas. Por consiguiente, se toma como referente el EIEM (Alsina, 2019, 2020) que se fundamenta en tres pilares interrelacionados: a) la Perspectiva Sociocultural del Aprendizaje Humano (Vygotsky, 1978), que entiende la educación como un fenómeno social y cultural que contempla el lenguaje y la interacción como herramientas esenciales para fomentar el aprendizaje; b) el Modelo Realista de Formación del Profesorado (Korthagen, 2001), que considera que los docentes deben de estar familiarizado con diversas maneras de intervenir y ejercitarlas en la práctica, es decir, deben tener criterio para saber cuándo, qué y por qué alguna situación es susceptible para reflexionar de forma sistemática; y c) la Educación Matemática Realista (Freudenthal, 1991), que promueve la utilización de problemas contextualizados en situaciones reales como inicio del proceso de enseñanza-aprendizaje de las matemáticas.
Con base en estos pilares, el EIEM (Alsina, 2019, 2020) considera la enseñanza de las matemáticas a través de secuencias didácticas que incluyen los siguientes tres niveles:
Nivel informal: la enseñanza de los contenidos matemáticos se prioriza desde contextos de situaciones reales y cercanas al alumnado, haciendo uso de materiales manipulativos y lúdicos, apoyándose, a su vez, en el conocimiento informal, el sentido común y la experiencia. En estos contextos, las demandas cognitivas que se movilizan son: la exploración, la manipulación o la experimentación, conformándose como requisitos para visualizar y comprender las ideas matemáticas de forma concreta.
Nivel intermedio: la enseñanza de los contenidos continúa en contextos que se configuran como puente entre los contextos de la fase anterior y los contextos formales de la fase posterior. Se incluyen en este nivel, recursos literarios (cuentos y canciones) y tecnológicos (Applets, robots educativos programables, etc.). En estos contextos, las exigencias cognitivas se centran en: la exploración y la reflexión, que facilitan de manera progresiva la esquematización y generalización del conocimiento matemático.
Nivel formal: la enseñanza del contenido termina en contextos gráficos y simbólicos donde se fomenta la representación y formalización del conocimiento matemático, haciendo uso de procedimientos y notaciones convencionales para promocionar el aprendizaje de lo concreto a lo simbólico. En estos contextos, pues, las exigencias cognitivas se centran principalmente en: la abstracción y la generalización.
Desde este enfoque se apuesta por la actividad heurística más que la pura ejercitación, y el pensamiento matemático crítico más que la simple repetición (Alsina, 2019).
Como se ha indicado en la introducción, este estudio se focaliza en la enseñanza de patrones. Cuando hablamos de patrón, nos referimos desde nuestro punto de vista, a una secuencia de elementos ordenados de acuerdo con una norma, regla, núcleo o unidad periódica determinada. Clements y Sarama (2015) exponen que la enseñanza de patrones persigue, precisamente, la búsqueda de regularidades y estructuras matemáticas. Es así como reconocer patrones se configura como una capacidad fundamental para muchos dominios del conocimiento como la lectura, las matemáticas o las artes, puesto que los patrones aportan significado y cohesión (Björklund y Pramling, 2014). Por esta razón Papic (2015) sugiere la necesidad de promover la conciencia de los niños y las niñas sobre los patrones para estimular el desarrollo estructural, la comprensión relacional y la generalización desde una edad temprana y, aunque de forma emergente, sentar las bases del pensamiento matemático en general y algebraico en particular. No podemos obviar que un pensamiento algebraico consolidado requiere capacidad para simbolizar y generalizar (Sibgatullin et al., 2022).
En nuestro estudio se asume que los patrones pueden variar según su regularidad y contenido; y que atendiendo a esta afirmación los patrones pueden presentar unidades que se repiten; que se ordenan de manera estructural o simétrica; o que crecen (Bock et al., 2018). La tipología de patrón que se aborda en nuestro itinerario de enseñanza son los de repetición. Es decir, patrones que mediante secuencias iterativas muestran regularidades o repeticiones de características cualitativas y/o cuantitativas específicas (color, formas, tamaño, sonidos, o números, por ejemplo, “verde, verde, amarillo, verde, verde, amarillo” o “■○■○”).
Autores e instituciones de prestigio señalan que la enseñanza de patrones de repetición y la comprensión de su estructura influye positivamente en el desarrollo matemático temprano, puesto que promueve un cimiento veraz para el pensamiento algebraico (Mulligan et al., 2020; Rittle-Johnson et al., 2018; Wijns et al., 2019). Desarrollar el concepto de patrón implica percibir la regla subyacente e identificar de manera consciente y funcional la unidad de repetición. De acuerdo con Wijns et al. (2019) es necesario apostar por la implementación de tareas con patrones que den la oportunidad a los escolares de transitar del pensamiento recursivo al funcional, es decir, de observar la relación consecutiva de elementos que yace en una seriación, para de manera guiada y acompañada lograr abstraer y representar la estructura interna de su núcleo.
Ahora bien, ¿qué implica la representación en matemáticas? Para Freudenthal (1991) el desarrollo progresivo de la representación de las ideas y procedimientos matemáticos va de lo concreto a lo abstracto, de manera que puede tener formas diversas a través de objetos físicos, lenguaje natural, dibujos y símbolos convencionales. Según afirma Reed (2001, p. 215), “dibujar puede ser una ventana a la mente de un niño”. Por tanto, es necesario respetar y favorecer el proceso de la representación con la finalidad de aprender (y sobre todo comprender) el símbolo que representa un objeto, una situación o una idea matemática. Es por esta razón que Duval (1995, p. 15) considera que “no hay conocimiento que pueda ser movilizado por un individuo sin una actividad de representación”. Asimismo, en relación con la representación como un proceso matemático que externaliza la comprensión del alumnado, Pino-Fan et al. (2017) aseguran que dicho proceso tiene un rol fundamental con la adquisición y el tratamiento del conocimiento de un individuo. Desde este prisma, el NCTM (2014) apuesta por una enseñanza de las matemáticas que permita establecer conexiones entre representaciones para así vincular de manera eficaz la comprensión conceptual y procedimental.
Considerando estos antecedentes, conceptualizamos la representación en matemáticas como un proceso interconectado que permite plasmar de manera concreta, a través de la utilización de diferentes signos, gráficos y/o lenguaje natural, el conocimiento y procedimientos matemáticos que poseen los alumnos. De esta manera se consigue organizar, comprender y comunicar la naturaleza matemática de acciones previamente realizadas en el plano educativo y social.
2. Metodología
El presente estudio se desarrolla desde un enfoque cualitativo para comprobar las oportunidades de comprensión que brinda el contexto más concreto (situaciones reales) y el más abstracto (recursos gráficos) del EIEM (Alsina, 2019, 2020) cuando se enseñan patrones de repetición al alumnado de educación infantil (4-6 años). De acuerdo con Maldonado (2018), este enfoque apuesta por la interpretación, descripción, análisis y comprensión de información cualitativa obtenida a través de grabaciones, observaciones, entrevista, etc. En consonancia con esta aportación, nuestro diseño facilita un análisis descriptivo e interpretativo que permite mostrar, mediante la representación en matemáticas de los alumnos, los resultados obtenidos de manera longitudinal en el nivel informal, concretamente en el contexto de situaciones reales, haciendo una comparativa con los resultados recogidos en el nivel formal (recursos gráficos).
2.1. Diseño y procedimiento
Como se ha indicado, se han seleccionado las actividades enmarcadas en los contextos de situaciones reales y recursos gráficos que conforman el EIEM. Las seis propuestas han sido sometidas a un juicio de expertos donde se han valorado: a) aspectos didácticos, b) organizativos, c) metodológicos, y d) pedagógicos del itinerario didáctico. Este procedimiento, junto con la práctica reflexiva desarrollada después de cada sesión, han favorecido la articulación de análisis continuos y retrospectivos que informan sobre el diseño y facilitan su mejora longitudinalmente. Se puede ampliar dicho procedimiento en Acosta y Alsina (2020) cuando validaron y aplicaron un itinerario de patrones de repetición con escolares de 3 años.
La implementación se ha llevado a cabo de manera longitudinal, con 24 escolares españoles pertenecientes todos a una misma clase de un centro de educación público. La muestra está conformada por 12 niños y 12 niñas. La edad promedio de la muestra es de 4,8 años y 5,8 años para los dos cursos escolares correspondientes a la intervención. Se ha seleccionado este grupo por las facilidades de acceso; por la continuidad y seguimiento longitudinal de la maestra tutora; y por estar considerado un centro con baja movilidad de matrícula en cursos preescolares.
Seguidamente en la tabla 1 se muestran las actividades diseñadas y validadas para escolares de 4 a 6 años.
La intervención se lleva a cabo en grupo reducido (12 niños y niñas) para facilitar la atención individualizada y la recogida de evidencias específicas y personalizadas. Dicha distribución de participantes se realiza de manera aleatoria y se mantienen los dos subgrupos de 12 alumnos durante toda la intervención. Por tanto, de manera longitudinal, se destinan un total de ocho sesiones de intervención directa para el contexto de situaciones reales y cuatro sesiones para el de recursos gráficos, con una duración de 50 minutos cada una. Cabe destacar que previamente a la intervención, se obtuvo el consentimiento informado de todas las familias.
Las sesiones se dividieron en tres fases: a) introducción de la propuesta, b) interacción y desarrollo, y c) representación y reflexión. Es importante destacar que en la fase final el alumnado representa de memoria el patrón que ha identificado en la actividad sin tener delante el modelo. El rol del docente es de guía e incitador de aprendizaje a través de preguntas intencionadas (NCTM, 2014) que inviten a generar conocimiento compartido con el grupo de iguales. Deben evitarse preguntas que no impliquen razonamiento, ni argumentación por parte de los escolares y que se contesten con un “sí” o un “no”.
2.2. Recogida de datos
La recogida de datos contempla tres herramientas: i) esquemas metodológicos etnográficos de observación participante donde se hace uso del diario de campo como instrumento para registrar expresiones espontáneas de los niños y las niñas durante la realización de las tareas; II) documentación pedagógica a través del registro audiovisual, fijo y móvil, de todas las sesiones; y III) producciones escritas, en formato dibujo, de todas las representaciones de los escolares como muestra de la formalización de los conocimientos adquiridos.
Kawulich (2006) considera la observación participante como una destreza que capacita a los investigadores para reflexionar y aprender sobre las propuestas que se desarrollan con participantes en un contexto natural, utilizando la observación y la participación activa como herramientas facilitadoras de una interacción directa y sin interferencias. Por su parte, la documentación pedagógica adopta un carácter reflexivo que da voz al pensamiento del niño, reconociendo al observador como un agente activo que co-construye significado de manera reflexiva, activa y recíproca con la finalidad de crear un espacio plural y transformador (Mitchelmore, 2018). No podemos obviar que las expresiones verbales y no verbales son claves para interpretar los conocimientos y habilidades de los escolares más pequeños (Björklund et al., 2020).
2.3. Análisis de los datos obtenidos
Las producciones infantiles, recogidas en formato de dibujo, se han categorizado siguiendo el diagrama que se muestra a continuación con la intención de eliminar el sesgo que genera una presencia jerarquizada de propuestas de acuerdo con el modelo que plantea el EIEM (Alsina, 2019, 2020). Se considera la categoría “correcto” cuando la representación no presenta errores e “incorrecto” cuando la producción presenta error en su estructura.
A partir de la información mostrada en la figura 1, se realiza un análisis cuantitativo donde se describen las variables categóricas según el número y porcentaje de casos en cada categoría.
Con la intención de complementar los datos anteriores, se transcriben y discuten las evidencias audiovisuales a través de un análisis interpretativo del discurso. Este análisis de los fragmentos más relevantes permite revisar las relaciones entre los textos y la realidad haciendo visible el discurso utilizado por el niño, su punto de origen, cómo fluye, y qué lo acompaña (Leeuwen, 2008). Esta información se triangula y contrasta con los datos cuantitativos, con las notas de campo registradas y con las producciones escritas de los niños y las niñas, para así mostrar también el rol que adopta el docente.
3. Resultados
Considerando el propósito de nuestro estudio, se analizan los resultados obtenidos longitudinalmente en contextos de situaciones reales y recursos gráficos, con la intención de comprobar cómo influye el contexto de enseñanza en la comprensión y representación de tareas con patrones de repetición.
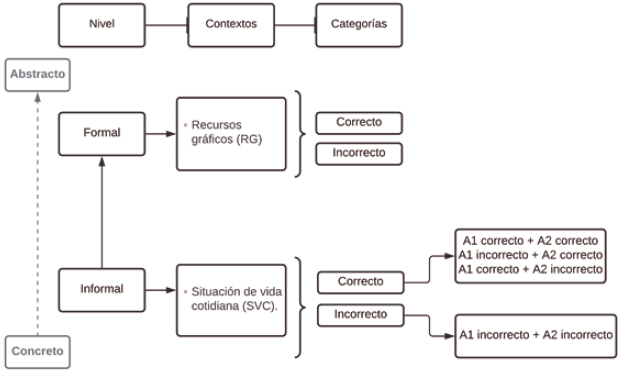
Como se aprecia en la tabla 2, el 85 % de casos válidos realizó correctamente la representación del patrón identificado en las actividades que se desarrollan en el contexto de situaciones reales, frente a un 15 % que no logró desempeñar la tarea con éxito. Sin embargo, se observa un aumento significativo de errores en el contexto de recursos gráficos, situándose en un 54,2 %. El grado de éxito en este contexto es solo del 45,8 %.
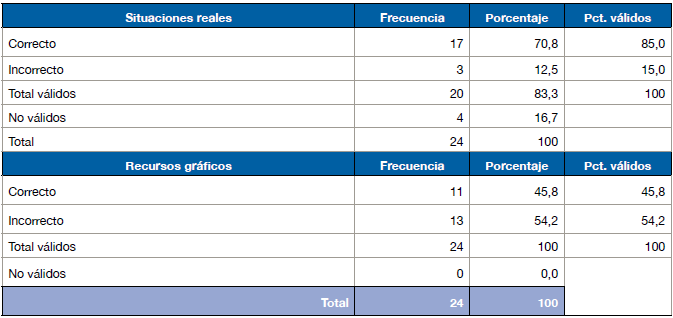
A continuación, se muestran los resultados correspondientes a 5-6 años.
De acuerdo con la información que se aprecia en la tabla 3, el 100 % de casos válidos representaron sin errores los patrones identificados en el contexto de situaciones reales, mientras que en el contexto de recursos gráficos solo lo hizo el 69,6 %. Observamos que, en comparación con la intervención del año anterior, las representaciones incorrectas disminuyeron un 23,8 %.
En la tabla 4 mostramos algunos ejemplos de la implementación. Por razones de espacio se selecciona uno para cada contexto y edad.
Seguidamente, se exponen algunos ejemplos de representaciones y transcripciones de diálogos obtenidos durante la implementación pedagógica para ilustrar el rol del docente como generador y promotor de aprendizaje.
A partir de los ejemplos que se muestran en la tabla 5, podemos observar cómo la justificación del alumnado, a pesar de la realización correcta, es más elaborada y consolidada en el contexto de situaciones reales que en el de recursos gráficos. De la misma manera, se aprecia cómo el docente a través de buenas preguntas, es decir, de intervenciones abiertas y con un lenguaje matemático preciso, invita e incita al alumnado a comunicar, justificar y razonar sus respuestas. Este escenario permite una discusión constructiva, desde una perspectiva paralela vivida por otro participante, que favorece un enriquecimiento y conceptualización para aquellos escolares que no han tenido éxito en la tarea (Vygotsky, 2004).
4. Discusión y conclusiones
Este estudio ha investigado cómo influye el contexto de enseñanza en la realización de tareas con patrones de repetición. Para ello, se analizaron las producciones escritas del alumnado para determinar si eran capaces de representar correctamente patrones de repetición en el contexto más concreto (situaciones reales) y en el más abstracto (recursos gráficos) de un itinerario de enseñanza de patrones previamente diseñado y validado. A partir de este análisis, se identificó una diferencia positiva del 32,9 % de las situaciones reales frente a los recursos gráficos en el alumnado de 4-5 años; en el alumnado de 5-6 años, aunque la diferencia entre ambos contextos disminuyó ligeramente, seguía siendo superior al 30 %.
Si se analizan los resultados de manera longitudinal, un 15 % de participantes de 4-5 años han representado de manera incorrecta los patrones en tareas planteadas a partir de situaciones reales, mientras que el porcentaje de incorrectos desciende al 0 % a los 5-6 años. En el contexto de recursos gráficos, las representaciones incorrectas disminuyen en un 23,8 %, siendo de 54,2 % para 4-5 años y de 30,4 % para 5-6 años. Sin embargo, a pesar de este descenso de errores, de manera general los y las participantes muestran dificultad para representar el patrón sin una previa interacción o manipulación de elementos concretos que conforman la unidad de repetición. En otras palabras, los datos obtenidos han evidenciado que la comprensión es más precisa en contextos en los que se prioriza la enseñanza a partir de situaciones informales de exploración de un entorno cotidiano y cercano a los niños y las niñas, donde es más fácil establecer relaciones con sus conocimientos previos. En este sentido, Castro y Castro (2016) señalan que aprenden a través de experiencias concretas con materiales y mediante interacciones lúdicas intencionadas y previamente planificadas. En esta misma línea, Zhong y Xia (2020) subrayan que la niñez necesita oportunidades de exploración, manipulación y experimentación, para de esta manera fomentar el aprendizaje desde una perspectiva lúdica y concreta.
Focalizándonos en las representaciones de los patrones, estamos de acuerdo con Alsina (2016) cuando señala que la representación de ideas y procedimientos matemáticos es un proceso indispensable para el aprendizaje, y por ello, si no hay representación no hay comprensión, y sin comprensión no puede haber aprendizaje de las matemáticas. Por ende, se puede asumir que, desde una edad temprana, los escolares deben representar para aprender matemáticas y así poder organizar, comprender y comunicar la naturaleza matemática de las acciones previamente realizadas en el plano educativo y social mediante la utilización de signos, gráficos y/o lenguaje natural. Esta es la razón principal por la que hemos tomado la representación en matemáticas como un proceso interconectado que permite: a) plasmar de manera concreta los conocimientos y procedimientos que poseen los niños y las niñas acerca de los patrones de repetición; b) evaluar el progreso en la comprensión de dichos patrones, y c) reequilibrar el proceso de enseñanza de patrones a través del diseño de tareas contextualizadas que fomentan y extienden el aprendizaje.
Desde esta perspectiva, Laski y Siegler (2014) ponen de manifiesto que los materiales de aprendizaje concretos solo son efectivos en la medida en que las actividades diseñadas están alineadas con el proceso de representación mental deseado. Es por este motivo que las propuestas educativas se deben articular con la finalidad de aumentar la codificación de las características estructurales que conforman el patrón, para facilitar la representación. Carruthers y Worthington (2005) llegan a la conclusión que, cuando los docentes alientan a los escolares de 3 a 8 años a representar en papel sus ideas matemáticas, favorecen la comprensión del simbolismo abstracto.
Nuestro estudio ha aportado datos relevantes que muestran cómo el grado de éxito de la comprensión a través de la representación está condicionado por el nivel de abstracción del contexto donde se plantea la propuesta. En esta línea, se considera que es necesario planificar y estructurar tareas que contemplen diferentes contextos de enseñanza, para así ofrecer una intervención educativa respetuosa con las necesidades del alumnado, en la que es imprescindible fomentar el uso de contextos concretos e informales que permitan ir avanzando hacia la generalización y formalización del conocimiento, evitando un tratamiento de los patrones exclusivamente de papel y lápiz. Este enfoque requiere, por una parte, conocimientos disciplinares sobre lo que se desea enseñar (NCTM, 2014; Pincheira y Alsina, 2021); y por otra, habilidades didácticas y metodológicas para tratar un concepto o procedimiento determinado a partir de diferentes contextos de enseñanza (Alsina, 2022). En esta línea, Villalpando et al. (2020) señalan que el profesorado debe traducir el currículo oficial a un lenguaje real que permita otorgar significado a la práctica docente, para así acercar los contenidos académicos a los escolares de manera reflexiva, competente y vivencial.
Llegados a este punto de discusión, compartimos la idea de que las situaciones educativas son sensibles al contexto, al ponerse en evidencia que el éxito de la representación ha estado estrechamente ligado con la comprensión del patrón y dicha comprensión ha sido más exitosa en el nivel más concreto del EIEM, en el que se prioriza la enseñanza de contenido matemático a partir de situaciones reales o cercanas a los niños y las niñas. Se ha evidenciado, además, como a través de buenas peguntas se promueve, genera y consolida conocimiento compartido. Por esta razón, alentamos a los docentes a apostar por el acompañamiento de la enseñanza de patrones de repetición desde una visión dialógica y multimodal que contemple diversos escenarios educativos que transiten de manera progresiva de contextos concretos a abstractos. Por ende, nuestra finalidad es que estas experiencias reales acompañen, mediante la reflexión, la acción docente futura (Radford y Sabena, 2015) y que nuestras conclusiones sean motivo de inspiración, sin pretender ser directamente generalizables a otras realidades, puesto que el número reducido de nuestra muestra lo dificulta. En esta línea, también asumimos como limitación de nuestro estudio el uso diferido, a través de imágenes, de situaciones reales en la primera etapa del itinerario didáctico, puesto que puede haber influido en las respuestas del alumnado, y es posible saber con certeza si los errores habrían disminuido con una implementación en un contexto real directo. Como futuras líneas de investigación, nos proponemos seguir evidenciando cómo influyen los otros contextos del EIEM en la enseñanza de patrones de repetición, analizando a su vez la relación que se establece entre el conocimiento matemático del alumnado y la habilidad para justificar y argumentar sus respuestas.