Introducción
La educación no puede competir con el avance de la tecnología. Lo que puede hacer es usar a la tecnología como un complemento para optimizar la consecución de los objetivos relacionados al proceso de enseñanza-aprendizaje. Sin embargo, la tecnología no podrá enseñar a pensar a los seres humanos, esto solo lo puede realizar un profesor que se valga de estrategias para poder estimular el pensamiento adecuadamente. Precisamente, si un docente utiliza a las paradojas como recursos educativos en sus sesiones de clase, logrará algo que la tecnología de nuestro tiempo aún no puede, esto es, provocar el debate, enriquecer el pensamiento y generar distintos puntos de vista que tengan por meta resolver alguna cuestión controversial.
El objetivo de esta investigación es proporcionar una metodología de enseñanza a los docentes que los oriente a buscar paradojas para que con ayuda de estas puedan mejorar los contenidos que difunden en sus sesiones de clase.
El problema que se busca resolver se relaciona con el pobre nivel educativo que la sociedad actual tiene. ¿De qué modo las paradojas deben ser utilizadas en sesiones de clase para que se pueda mejorar el proceso de enseñanza-aprendizaje?
Frente a esta cuestión, en este escrito se defiende la idea de que las paradojas sirven como disparadores educativos que motivan al estudiante a dar su opinión o perspectiva sobre el asunto problemático que está siendo presentado en clase. En ese sentido, el uso de las paradojas en las sesiones de clase resulta más que necesario para lograr los objetivos planteados por el docente.
Hoy en día, la tecnología presenta una serie de estímulos visuales y auditivos con los cuales el docente no puede competir pues se encuentra en clara desventaja. Con un simple smartphone, un joven puede buscar en internet cualquier cosa de la que tenga duda y, además, se puede entretener mediante los videojuegos. Por lo anterior, resulta imprescindible dotar al maestro de herramientas cognitivas que le ayude a estimular el pensamiento de sus alumnos para que pueda hacer de la enseñanza un evento más interesante que el que ofrece la tecnología en la actualidad.
La metodología utilizada en este trabajo se basa en un enfoque cualitativo (Sampieri et al., 2014). Se ha recurrido al método filosófico del análisis lógico-lingüístico dentro de los límites de la filosofía analítica (Salazar Bondy, 2000). Así, se respetarán los criterios de claridad en la terminología. En lo que toca a la argumentación, se prueba toda afirmación relevante a nivel filosófico. Ahora bien, para lograr realizar esta investigación se recurre a la técnica de la lectura de las fuentes de la recopilación documentaria y de análisis documental, es decir, se revisa diferentes bases bibliográficas y se ha realizado el análisis filosófico respectivo. En cuanto a los instrumentos, se han utilizado fichas de investigación (textuales, de resumen, de paráfrasis y mixtas) para seleccionar las citas relevantes respecto a nuestro tema. También, se ha guardado información encontrada en la web en un USB y se han usado los medios electrónicos disponibles para tipear información, así como para facilitar la comunicación fluida entre los investigadores. Finalmente, el procedimiento que se ha seguido es el siguiente: se revisaron fuentes bibliográficas, se eligieron diversos autores (que conforman el marco teórico de este trabajo), se inició la búsqueda de los archivos electrónicos relativos a la temática en estudio, se clasificó los datos, es decir, se distinguió entre libros, artículos de revista y publicación de periódicos, entre otros que nos permitan defender nuestra investigación, por último, se interpretó adecuadamente las publicaciones que se seleccionaron y procedió a realizar este escrito.
En cuanto a la estructura de este documento, se debe mencionar que este escrito inicia aclarando los conceptos de falacia y reducción al absurdo. Enseguida, se analiza una lista de paradojas, pero con el objetivo de que puedan ser utilizadas en un aula de clase. Así, se trata sobre algunas paradojas como la paradoja de Aquiles y la Tortuga, la de Galileo, la del hotel de Hilbert, la de Tristam Shandy, la de Protágoras, etc. Finalmente, se cierra este trabajo tratando de explicitar el aspecto afectivo y emocional que un estudiante experimenta cuando trata con estas paradojas.
Una estrategia educativa
La educación en el Perú atraviesa desde hace tiempo serias dificultades. A nadie le sorprende el bajo nivel educativo que aparece reflejado en las pruebas PISA (Programme for International Student Assessment) (Gestión, 3 de diciembre del 2019). Además, el escándalo de plagio detectado en las tesis de varios personajes mediáticos pone en entredicho si realmente tiene salvación el sistema educativo peruano.
El alumno promedio en el país tiene por cultura general a los youtubers, a los influencers y a los reggaetoneros de moda. La mayoría prefiere ver Netflix, algún programa de farándula y memes de alguna red social juvenil como TikTok. Muy pocos valoran la cultura, el genio, la creatividad, la lectura, los libros, las grandes películas clásicas, el teatro nacional, etc. Por este motivo, quien quiera ser educador en estas circunstancias debería recibir una medalla si realmente quiere cambiar este calamitoso estado de cosas.
Ser educado no significa solo conocer o saber de memoria algunos datos; a esto se le tendría que llamar “ser instruido”. Una persona educada conoce los temas sobre los que investiga, pero también es alguien que está formada en valores. Tener valores significa ser una persona que está dispuesta a vivir con dignidad, que quiere ayudar a los demás a entender la importancia de la justicia social y que entiende que la solidaridad no es un rasgo de debilidad, sino un gesto de nobleza hacia todos nuestros semejantes.
En la educación confluyen muchos factores, pues es una actividad compleja. Sin embargo, podemos concentrarnos en la cuestión de cómo organizar el proceso de enseñanza-aprendizaje. Lo que distingue a un profesor de otro es el modo de utilizar los recursos didácticos con el objetivo de que sus alumnos obtengan algún saber determinado, asociado a algún valor moral.
Lo ideal sería conseguir que el alumnado desarrolle su pensamiento crítico; esta habilidad se manifiesta en diversas actividades como realizar preguntas relevantes, hacer distinciones, buscar contraejemplos, sugerir clasificaciones, analizar afirmaciones, proponer hipótesis, definir conceptos, descubrir opciones no tan evidentes, poner en evidencia supuestos, buscar las causas, ordenar las razones que sustentan una tesis dada, detectar las relaciones entre las partes y el todo, conectar ideas, argumentar consistentemente sin caer en falacias, apreciar la importancia del contexto para estudiar algún hecho social, etc. (Rosas et al., 2018). Lo que resulta más que interesante es que el alumno pueda elaborar una argumentación coherente, sólida y con claridad usando la lógica para ello (Torres da Silva, 2016).
Lograr que los alumnos mejoren su pensamiento crítico para que ellos mismos tengan el interés de cultivarlo debería ser el objetivo central de la educación.
Al respecto, hay dos modos de educar que han sido superados. El estilo tradicional de educar, en el cual el profesor era considerado la fuente del saber que el estudiante debe procurar conocer, hoy se considera insuficiente. El otro estilo, el conductista, que consideraba que el alumno debía seguir las instrucciones de su maestro e imitarlo en todo, también se considera incompleto. En esta época el método más adecuado para enseñar se basa en teorías del aprendizaje de tipo constructivista representado por Piaget, Ausubel, Bruner y Vigotsky (Solé y Coll, 1995). Afirmamos que este método es más adecuado porque considera al alumno como el centro del aprendizaje (como lo sugiere Gutiérrez-Pozo, 2023) y, además, porque el concepto de “competencia” que se viene utilizando para diseñar los sílabos y los planes curriculares es compatible con el marco teórico del constructivismo, pues exige consciencia del estudiante acerca de su aprendizaje y también una posición crítica sobre lo que está aprendiendo.
El constructivismo sostiene “que las personas forman o construyen gran parte de lo que aprenden y comprenden” (Schunk, 2012, p. 229). De acuerdo con esta posición, el alumno puede construir su propio conocimiento si tiene realmente la intención de aprender. La tarea del profesor debe consistir en diseñar las condiciones adecuadas para que la actividad creadora y autónoma del alumno pueda iniciar. Escribe Schunk:
Otro supuesto del constructivismo es que los profesores no deben enseñar en el sentido tradicional de dar instrucción a un grupo de estudiantes, sino que más bien deben estructurar situaciones en las que los estudiantes participen de manera activa con el contenido a través de la manipulación de los materiales y la interacción social (Schunk, 2012, p. 231).
Asimismo, el alumno no puede aprender en soledad, sino que más bien debe tener un espíritu colaborativo de tal modo que pueda trabajar en comunidad con sus demás compañeros. La idea es que el conocimiento se debe obtener mediante una actividad compartida (Schunk, 2012). La siguiente tabla provee una idea acerca de cómo son creados los ambientes de aprendizaje siguiendo principios constructivistas.
Tabla 1 Principios que rigen los ambientes de aprendizaje constructivistas

Fuente: Brooks y Brooks, 1999 (citado en Schunk, 2012, p. 261).
Una estrategia constructivista es la del aprendizaje basado en problemas (ABP) (Escribano y Del Valle, 2008). Estas son las características fundamentales de este método:
• El aprendizaje está centrado en el alumno.
• El aprendizaje se produce en pequeños grupos.
• Los profesores son facilitadores o guías de este proceso.
• Los problemas son el foco de organización y estímulo para el aprendizaje.
• Los problemas son un vehículo para el desarrollo de habilidades de resolución de problemas.
• La nueva información se adquiere a través del aprendizaje autodirigido (Manzanares, 2008, p. 15).
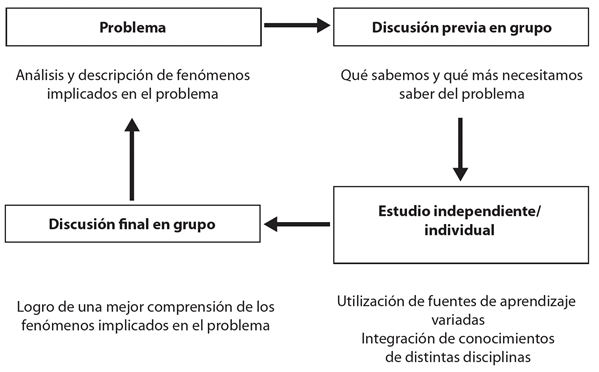
Desde esta estrategia, el docente en tanto tutor o guía presenta un problema al estudiante para que lo vaya resolviendo con su grupo de trabajo. Juntos se encargan de investigar, leer y consultar para poder llegar a una solución o al menos para lograr una comprensión mejor de la cuestión analizada. Después, se reúnen para poder discutir sus resultados y así cumplir con la actividad encargada por el docente. Este es un modo efectivo de desarrollar el pensamiento crítico. La figura 1 ilustra lo anterior.
Ahora bien, la idea es que el tipo de problema más interesante, que aún no ha sido explorado de modo suficiente por los docentes, es el problema generado por el hallazgo y la exposición de una paradoja. Las paradojas pueden ser aliadas en el proceso de enseñanza-aprendizaje y su uso puede beneficiar a la actividad educativa tanto en el aspecto del logro de competencias como en la formación moral del educando. Esta investigación se ha realizado con base en un estudio documental de fuentes escritas así como de Internet.
En ese sentido, se procederá a exhibir a las paradojas como recursos didácticos en términos educativos. Así, en principio, se distingue entre falacia y paradoja para mostrar cómo es posible que una paradoja pueda ser “resuelta” al descubrirse que, en realidad, se trataba de un argumento basado en un error de razonamiento poco perceptible. Además, se considera importante el enfoque de las paradojas como elementos contradictorios que pueden ser utilizados en pruebas por reducción al absurdo. Luego, se desarrolla una lista de paradojas, en parte superadas por la tradición, para reforzar nuestra perspectiva de que las paradojas pueden eventualmente resolverse y también para revelar el aspecto educativo y didáctico de las mismas.
Falacias y paradojas
Tanto las paradojas como las falacias tienen la forma de argumentos. Sin embargo, mientras que las paradojas son argumentos que procediendo lógicamente desembocan en una contradicción inesperada, las falacias son argumentos lógicamente inválidos pero persuasivos a nivel psicológico (Copi y Cohen, 2001). Las falacias se producen cuando un argumento parece aceptable, pero en realidad esconde algún error que no es detectable a simple vista. Por ejemplo, la falacia ad ignorantiam puede parecerle correcta a algunos. Esta falacia se presenta cuando alguien afirma casos semejantes al siguiente: “como nadie ha probado de modo concluyente que Dios no existe, entonces tenemos que aceptar que en verdad Dios existe”. Lo cierto es que, en ausencia de pruebas, nada podemos afirmar ni negar sobre cualquier asunto dado. Otro ejemplo lo constituye la falacia del espantapájaros. Enseguida, se analiza el siguiente caso. Dos candidatos al congreso debaten. Uno dice que es vegano porque ama a los animales; el otro aprovecha eso y dice que él también ama a los animales, pero sobre todo ama a los pobres, a las madres solteras y a los niños sin hogar, dando a entender que su contrincante solo ama a los animales, pero desprecia todo lo demás. Cuando se nota que en una declaración se le adscribe al contrincante una serie de ideas que no ha mencionado explícitamente, se está ante un caso de falacia del espantapájaros. Esta es muy usual en política.
En relación con las paradojas ha existido el intento de parte de los estudiosos de reducir las paradojas a falacias para probar que escondían algún error. El propio Russell intentó probar que la paradoja de Cantor no era más que una falacia, pero falló en esa empresa. No obstante, lo que obtuvo no fue poco, pues al estudiar dicha paradoja pudo digerir los insumos suficientes como para proponer su propia paradoja tan o más desestabilizadora que la paradoja del máximo número cardinal de Cantor (Garciadiego, 1992).
La revelación de que tal o cual paradoja ha sido desbaratada como una simple falacia ha sido objeto de polémicas. Sin embargo, aunque una paradoja haya logrado ser desenmascarada como una vil falacia, nadie duda de su valor propedéutico. La paradoja, en tanto problema que llama nuestra atención, nos enseña que existen límites en nuestra comprensión de algún fenómeno. Siempre esos límites pueden ser superados, pero el aprendizaje que hemos obtenido al procurar responder al reto planteado por la paradoja ha sido muy valioso. Precisamente, es este aspecto educativo de la paradoja lo que podría ser rescatado, a pesar de la superación epistémica y cognoscitiva de la misma.
Paradoja y reducción al absurdo
Aunque no siempre es el caso, uno de los ingredientes habituales de las paradojas es la contradicción. En la lógica, la contradicción ha sido utilizada de manera conveniente sobre todo en aquellos razonamientos clasificados como “reducción al absurdo”.
La estructura de la reducción al absurdo parte por una suposición. Luego, si de esa suposición se deduce tanto P como la negación de P, entonces podemos negar la suposición inicial. Por ejemplo, esta prueba fue utilizada por Euclides con éxito para probar que no existe un último número primo. Asimismo, mediante la reducción al absurdo es posible probar que la raíz de dos no es un número racional. Veamos un caso más sencillo. Supongamos que se afirme que la araña es un insecto. Si fuera así, tendría seis patas. Pero tras un examen notamos que, en realidad, no tiene seis sino ocho patas.
Así podemos deducir que no es cierto que la araña sea un insecto. Este es un caso sencillo de reducción al absurdo. El esquema lógico de la reducción al absurdo sería el siguiente: (P (QQ)) P. Lo anterior se puede entender del siguiente modo. Si alguien afirma que P y esto nos lleva a contradicciones tipo QQ, entonces lo que se debe aceptar es que P.
Esta es la manera en que algunas paradojas han sido utilizadas por la tradición intelectual. La demostración de A se llevaba a cabo de este modo. Si la falsedad de A llevaba a paradojas, entonces esto probaba que A no era falsa, sino más bien verdadera. Es necesario revisar un ejemplo usado por San Anselmo de Canterbury (trad. en 1998) para probar la existencia de Dios. Según este pensador, cuando se dice que Dios es aquello más grande que pueda ser pensado, cualquiera que escuche esta definición puede estar de acuerdo y, por ese solo hecho, Dios pasaría a existir como concepto en su mente. La cuestión es si Dios puede existir solo como concepto dentro de la mente humana y no como una realidad fuera de la mente humana. Vamos a plantear una prueba por reducción al absurdo. Si es falso que Dios pueda existir fuera de la mente, eso plantearía un problema. Por un lado, Dios es lo más grande por definición, pero, por otro lado, si Dios no existiera fuera de la mente, entonces no sería tan grande como se planteó en un inicio pues tendría una existencia limitada. Esta es una paradójica contradicción. Por lo tanto, es verdad que Dios puede existir también fuera de la mente. A esto se le conoce como argumento ontológico.
Las paradojas no solo tienen el objetivo de desconcertar a la audiencia, también pueden ser utilizadas para reforzar una idea o para discutir conceptos fundamentales de alguna disciplina. En este sentido, las paradojas pueden ser utilizadas como recursos didácticos. En lo sigue, se examina las siguientes paradojas: la de Aquiles y la Tortuga, la de Galileo, la del hotel de Hilbert, la de Tristam Shandy, la de Protágoras, la de Monty Hall, la de Dios y la piedra, la de Epicuro, la de los viajes en el tiempo, la del huevo y la gallina y algunas paradojas geométricas. Esta investigación termina tratando de explicar qué es lo que siente un estudiante cuando su profesor o profesora le presenta una paradoja. A continuación, se estudiará la paradoja de Aquiles y la tortuga.
Paradoja de Aquiles y la Tortuga
Esta paradoja aparece en el capítulo 9 del Libro VI de la Física de Aristóteles (trad. en 1995) y fue planteada por Zenón de Elea para probar que el movimiento es absurdo. Para lograr este objetivo, el discípulo de Parménides imagina una supuesta carrera entre Aquiles y una tortuga. Como Aquiles es un experimentado corredor, le da una ventaja de 10 metros a la tortuga. La velocidad de Aquiles y la tortuga son 10 m/s y 1 m/s, respectivamente. Durante el primer segundo de esta carrera Aquiles ha llegado donde estaba la tortuga, pero para ese mismo momento la tortuga habrá avanzado un metro. Apenas Aquiles recorre ese metro, la tortuga habrá recorrido 0,1 metro. Cuando Aquiles recorra ese 0,1 metro, la tortuga habrá recorrido 0,01 metro y así sucesivamente. Dado que el espacio es infinitamente divisible, siempre existirá una pequeña cantidad de espacio que la tortuga habrá adelantado a Aquiles y, por lo tanto, Aquiles nunca podrá alcanzarla. Sin embargo, por otro lado, es obvio que Aquiles sí la alcanzará, porque el más rápido siempre alcanza al más lento y Aquiles es el más rápido. Esta es la paradoja.
Algunos consideran que la solución a este problema se basa en la idea de que una adición de infinitos sumandos no necesariamente da un resultado infinito. De hecho, si sumamos las cantidades que recorre Aquiles, a saber, 10 + 1 + 0,1 + 0,01 + 0,001 + … el resultado que obtenemos es 11 + 1/9, es decir, 11,. Esta cantidad es menos que 11,12. Por ende, podemos decir que Aquiles alcanza a la tortuga cuando recorre casi 11,12 metros (Sthal, 1971). Esta solución es polémica, pero es aceptable para un gran número de personas. Sin embargo, la enseñanza que esta paradoja nos provee puede ser utilizada en un aula de clase para poder motivar el aprendizaje. También se ha propuesto la idea de que esta paradoja se basa en una falacia, a saber, la falacia del continuo. Esta falacia sostiene que muchas diferencias pequeñas acumuladas no son relevantes para determinar si hay un cambio o no. Por ejemplo, dado que no se puede saber cuánto exactamente hay que quitarle a un rico para que se vuelva pobre, entonces no hay diferencia entre ser rico y ser pobre. Esto es incorrecto pues del hecho de que desconozcamos cuando se producen los cambios, no se infiere que las cosas no cambien. Ahora bien, debido a que la paradoja de Aquiles hace un uso pernicioso de la expresión “aunque no la habrá alcanzado estará cerca de lograrlo” (Mora, 2019), se puede afirmar que cae en la falacia del continuo pues asume que nunca se pasará del “estará cerca de alcanzarlo” a “lo alcanzó”. Enseguida, se revisará la paradoja de Galileo.
Paradoja de Galileo
Esta paradoja fue planteada por Galileo (1945) al reflexionar sobre la relación entre números naturales y números cuadrados. Si pensamos en los primeros diez números naturales, solo encontraremos tres números cuadrados. Si pensamos en los primeros 100 números naturales, solo encontraremos diez números cuadrados. Si pensamos en los 1000 números naturales, solo encontraremos 31 números cuadrados. Por ende, siempre habrá más números naturales que números cuadrados y se mantiene la idea de que el todo es más grande que la parte, siendo el todo conformado por números naturales y la parte, por números cuadrados. Ahora bien, ¿qué pasa si consideramos todos los números naturales los cuales son infinitos? Si los números naturales son infinitos, entonces los cuadrados también lo son. Pero si esto es así, entonces ya no se mantendría la idea de que el todo sea más grande que la parte porque el todo y la parte serían igual de infinitas. También se suele afirmar que lo que Galileo concluye es que las relaciones de mayor, menor e igual, no tienen el mismo sentido entre cantidades finitas que entre cantidades infinitas.
Este problema sería revisado más tarde por Georg Cantor. Y la solución que propone se basa en el uso del concepto de correspondencia biunívoca. La idea es que, efectivamente, el número de números naturales es el mismo que el número de números cuadrados, y esto puede comprobarse porque a cada número natural le corresponde un número cuadrado. Y sí, se tratan del mismo tipo de infinito, a saber, álef cero . Ahora bien, la sorpresa es que no existe un solo tipo de infinito sino toda una sucesión de números transfinitos. Por ejemplo, el número de números reales es más grande que el número de números naturales. Puede concluirse que lo que Galileo halló fue una paradoja desde el punto de vista de las matemáticas de su época. Sin embargo, desde otro marco teórico, a saber, el de las matemáticas del siglo XIX, esta situación ya no constituye una paradoja sino más bien un hecho. No obstante, de nuevo la enseñanza que esta paradoja nos deja es muy valiosa, pues revela que lo que llamamos “conocimiento” es relativo a un estadio del desarrollo científico. A continuación, se estudiará la paradoja del hotel de Hilbert.
Paradoja del hotel de Hilbert
El matemático David Hilbert (2013) planteó algunas curiosas ideas contraintuitivas sobre el infinito. En lo que sigue, se intentará simular una sesión de clase de un profesor de matemáticas. Imagínese un hotel de infinitas habitaciones. En un momento determinado llegan infinitos huéspedes. El hotel se llena y todas las habitaciones están ocupadas. Sin embargo, en ese momento llega un turista y pide una habitación. En este instante se le pregunta al aprendiz, ¿qué se puede hacer para que entre este nuevo huésped? Es preciso dejarlo pensar un momento. Luego de un tiempo prudencial se le dice que el asunto interesante es que, a pesar de estar lleno, el hotel podría organizarse de tal modo que se pudiera admitir a este nuevo huésped. Entonces, bajo las órdenes del gerente todos los visitantes se moverán a la habitación contigua y así, el nuevo visitante podrá obtener su habitación. Este impase se solucionó, no obstante, al rato ocurrió otro problema, pues llegó una excursión con infinitos huéspedes. De nuevo, se le vuelve a preguntar al aprendiz, ¿qué se puede hacer para que entre esta excursión de infinitos huéspedes? Otra vez, es preciso dejarlo razonar por un tiempo breve para después comentarle que, aunque pareciera que ya no pudieran admitirse más visitantes, este no es el caso. De nuevo, bajo las órdenes del gerente los huéspedes de las habitaciones n fueron movidos a una habitación 2n. De este modo, quedaban libres las habitaciones impares y dado que los impares son infinitos, la excursión pudo encontrar alojamiento.
David Hilbert ya era consciente de las travesuras del infinito. Estas paradojas, en realidad, son solo modos de difundir de modo más didáctico la extraña naturaleza del infinito. Sin embargo, queda claro que el modo de aprender a través de paradojas implica tratar de resolver estos desafíos mentales. La aceptación de estos retos hará del alumno alguien más preparado para la toma de decisiones en su vida diaria, pues habrá ejercitado de modo conveniente el pensamiento crítico. Enseguida, se analiza la paradoja de Tristam Shandy.
Paradoja de Tristam Shandy
Tristam Shandy (un personaje creado por Lawrence Stern) sostuvo que no le alcanzaría la vida para escribir sobre sus vivencias porque se dio cuenta de que tardó dos años en escribir acerca de sus primeros dos días de vida. Sin embargo, Bertrand Russell (1983) afirmó que hay un modo en que él puede escribir sobre toda su vida. ¿Cuál sería este modo? Debemos dejar pensar al alumno esta cuestión. Russell sostuvo que, si Tristam Shandy viviera infinitos años con elevada intensidad cada uno de sus días, el escritor podría escribir todo aquello que quisiera sobre cada uno de sus días de vida. Así, el día 1000 le llevaría escribirlo 1000 años y el día 1600 le llevaría escribirlo 1600 años. De acuerdo con Clark:
Esto es así porque cada par de días de vida pueden hacerse corresponder con un par sucesivo de años que tarda en redactar esos días, si bien su memoria necesitará retrotraerse cada vez más, sin límite. Por ejemplo, tendrá que redactar los días 101 y 102 alrededor de un siglo después, en los años 101 y 102, y los días, 1001 y 1002 los redactará casi un milenio después (2009, p. 239).
Llegados a este punto, debe quedar claro que hubo una época de la historia en la que los matemáticos se preocuparon mucho por la naturaleza del infinito. Uno también puede jugar con sus estudiantes proponiéndoles estos rompecabezas para que puedan, poco a poco, acostumbrarse a pensar de modo libre y creativo. A continuación, conoceremos la paradoja de Protágoras.
Paradoja de Protágoras
Esta paradoja también se conoce como la paradoja de los abogados. El primero en presentarla fue Aulo Gelio (cerca del año 150), pero Diógenes Laercio (1985) la volvería a escribir tiempo más tarde. Protágoras le enseñó abogacía a un tal Euatlo a cambio de la mitad de su paga, a condición de que completaría el pago de la enseñanza cuando ganase su primer juicio. Evidentemente, si perdía su primer juicio, no tenía que pagarle a Protágoras. Ambos aceptaron este pacto. Sin embargo, después de cierto tiempo Protágoras aún no recibía su dinero por haberle enseñado a su alumno, entonces le preguntó la razón y Euatlo respondió que no había podido pagarle porque todavía no había defendido ningún pleito, ya que se había dedicado a otras actividades. Protágoras en ese momento decidió demandarlo para que le pagase. Los dos ante el juez presentaron sus alegatos. Protágoras señaló que, pese al resultado del juicio, Euatlo debe pagarle, puesto que si Protágoras gana el juicio, Euatlo debe pagar porque el fallo del juez le obligaría y si Protágoras pierde el juicio, Euatlo debe pagarle pues de acuerdo con el pacto, Euatlo habría ganado su primer juicio y eso implicaba que cumpliera con cancelarle económicamente. Euatlo también quiso tomar la palabra. Él afirmó que no debería pagarle a su maestro porque del mismo modo, pese al resultado del juicio, él no estaría obligado a ello. Si Euatlo gana el juicio, entonces la demanda de Protágoras no tendría lugar y, por ende, el juez no podría obligarlo a pagar. Si Euatlo pierde el juicio, entonces habría perdido su primer juicio y de acuerdo con el pacto acordado, no debería pagarle. La pregunta desconcertante es: ¿quién tiene la razón? Es evidente que no pueden tenerla ambos.
Esta paradoja es muy apropiada formularla a alumnos de derecho de primeros años de universidad, pues permite conocer conceptos básicos de la carrera tales como demanda, alegato, juicio, pacto y demás. Sin embargo, también es útil para poder diferenciar entre la moral y el derecho y, en específico, entre las normas morales y las normas jurídicas. De este modo, el hecho de que un alumno le deba pagar a su profesor por lo aprendido se podría considerar un caso de norma moral, no obstante, el hecho de que los pactos y/o contratos se deban cumplir, se puede considerar como un caso de norma jurídica. Una forma de solución de esta paradoja estriba en determinar qué tipo de norma tiene mayor jerarquía. Leibniz propuso otra solución en su tesis doctoral titulada Disputatio Inauguralis de Casibus perplexis in Jure de 1666 (publicado en Artosi et al., 2013). Afirmó que Euatlo ganará el juicio, pero Protágoras podría volver a demandarlo. En este último caso, el fallo del juez sería favorable a Protágoras pues la condición de ganar su primer juicio ya habría sido cumplida por Euatlo. Enseguida, se expondrá la paradoja de Monty Hall.
Paradoja de Monty Hall
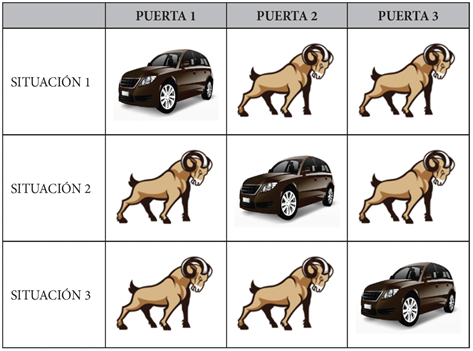
En 1975 la revista The American Statistician publicó la carta de Steve Selvin (1975) donde aparece esta paradoja. Mediante esta se pueden discutir conceptos vinculados a la teoría de probabilidades. En un programa concurso, el conductor llamado Monty Hall, ofrece a los concursantes un gran auto si es que eligen correctamente una puerta de tres que se ofrecen. Si pierden, se les dará un regalo consuelo, a saber, una cabra. Un concursante elige una puerta y el presentador no le abre la puerta elegida, sino que abre otra puerta detrás de la cual se descubre que no hay premio. En ese caso, Monty Hall le ofrece la oportunidad de cambiar de puerta o de quedarse con la elegida. El concursante comienza a dudar porque la situación pareciera ser utilizada por el presentador para, de algún modo, persuadirlo a cambiar de puerta. Pero, ¿debe o no debe cambiar de puerta el concursante?, ¿cuál es la opción que hará más probable que gane?
El análisis de esta paradoja permite estudiar con más detalle los conceptos fundamentales de la probabilidad. De hecho, esto ha sido investigado en Gea et al. (2017). Si consideramos que el premio solo se encuentra detrás de una de las tres puertas presentadas, entonces podemos decir que hay una probabilidad de 1/3 de ganar. El presentador del programa le abre una de las puertas que está vacía y le pregunta si quiere cambiar su elección. Esto podría interpretarse como que ahora la probabilidad de ganar es de 1/2, pero, de hecho, no es así. Lo que pasa en realidad es que cuando uno elige una puerta se pueden dar tres situaciones, a saber, el auto puede estar detrás de la primera, la segunda o la tercera puerta.
Primera situación: si hemos elegido la primera puerta ganadora en la que está el auto, el presentador nos mostrará una puerta vacía. En ese caso, si cambiamos, perdemos.
Segunda situación: si hemos elegido la primera puerta perdedora, el presentador nos mostrará una puerta vacía pues sabe que el auto se encuentra en la segunda puerta. En ese caso, si cambiamos, ganamos.
Tercera situación: si hemos elegido la primera puerta perdedora, el presentador nos mostrará una puerta vacía pues sabe que el auto se encuentra en la tercera puerta. En ese caso, si cambiamos, ganamos.
Esto indica que siempre que cambiamos, tenemos más posibilidad de ganar que de perder, específicamente, dos veces de tres en total. En consecuencia, lo recomendable es, a pesar de las apariencias, cambiar de puerta. Lo interesante de esta paradoja es que sirve para explorar conceptos matemáticos asociados a la probabilidad. A continuación, se estudiará la paradoja de Dios y la piedra.
Paradoja de Dios y la piedra
Esta paradoja, que tiene raíces medievales, pero aparece en Savage (1967), podría enseñarse en el curso de filosofía de la religión o incluso podría plantearse como desafío para estudiantes de teología. ¿Puede Dios crear una piedra tan grande que él mismo no sea capaz de levantar? Si la puede crear, entonces ya no la podrá levantar y, por ende, no lo podría todo. Si no la puede crear, entonces no lo podría todo. Considerando ambas opciones, se deduce que Dios no lo podría todo, es decir, no sería todopoderoso. Y si es así, ¿podemos seguir llamándolo Dios? Aquí se ponen en cuestión los conceptos de Dios y de omnipotencia.
Una versión física asociada a lo anterior se vincula con la paradoja del objeto inamovible versus la fuerza irresistible. Por un lado, un objeto inamovible es uno que nadie ni nada pueden mover. Por otro lado, una fuerza irresistible es una fuerza que no encuentra oposición, es decir, que nada le puede ofrecer resistencia. ¿Qué pasaría si un objeto inamovible se topa con una fuerza irresistible? Estamos ante otra paradoja.
Estas paradojas podrían replicarse bajo la idea de que las expresiones “Dios (que lo puede todo) crea una piedra tan grande que él no puede cargar” y “la fuerza irresistible (a la cual nada se le puede resistir) es resistida por un objeto inamovible”, son frases contradictorias a nivel semántico y, por lo tanto, razonar con ellas desemboca en paradojas. Lo mismo ocurre con frases tales como “el número par que también es impar”, “los solteros que están casados”, “los círculos cuadrados”, “el olor a azul”, etc. Todas estas frases son sinsentidos y, por ende, los objetos a los que aluden no existen. En el primer caso, Dios está condicionado por una acción que limita su naturaleza, cuando en principio, nada lo puede limitar. En el segundo caso, la fuerza irresistible también encuentra una limitación (el objeto inamovible) que destruye su propia definición. Lo que podría afirmarse es que no existen los mundos donde Dios cree una piedra que no puede cargar y donde una fuerza irresistible se encuentre con un objeto inamovible. Esto podría ser materia de discusión en un salón de clases de filosofía o, incluso, en uno de física. A continuación, conoceremos la paradoja de Epicuro.
Paradoja de Epicuro
Lactancio (trad. en 2014) en De Ira Dei atribuyó a Epicuro una paradoja al respecto de Dios (Hickson, 2014). Si Dios existe, ¿por qué permite la existencia del mal? Tal vez no sepa que existe. Si fuera así, Dios no lo sabría todo y esto es absurdo. Tal vez sí sepa que existe, pero no puede evitarlo. Si fuera así, Dios no lo podría todo y esto es absurdo. Tal vez sí sepa que existe y también puede evitarlo, pero no quiere evitarlo. Pero si fuera así, Dios no sería bueno y esto es absurdo. Entonces, ¿por qué Dios permite que el mal exista? Quizás lo haga para probarnos. Pero esto es inútil porque Dios, al ser omnisciente, ya sabe lo que ocurrirá y siendo así, no necesita probarnos. Tal vez esto sea culpa del diablo, sin embargo, si Dios es omnipotente y supremamente bueno, ya habría derrotado al diablo hace mucho tiempo. Otra opción puede ser la del libre albedrío. No obstante, ¿es posible que Dios pueda crear un mundo con libre albedrío y carente de maldad? Si no es posible, Dios no lo puede todo, lo cual es absurdo y si es posible, entonces Dios también creó al mal y eso no lo haría bueno, pero, nuevamente, esto es absurdo.
En la Teodicea,Leibniz (trad. en 2013) propone una manera de resolver la cuestión de la existencia del mal en un mundo creado por un Dios sumamente bueno. Dios sabe que la pura bondad no produce variedad, en cambio, un poco de maldad puede generar mayor bien que la sola bondad. Escribe Savater:
Pensemos, por ejemplo, en una biblioteca, y en una obra tan extraordinaria como la Ilíada. Una biblioteca que tiene la Ilíada está enriquecida por un libro importante. Pero imaginemos una biblioteca de diez mil volúmenes y que todos fueran la Ilíada. Se trataría de un lugar inferior, frente a otros que tuvieran la Ilíada y otros novecientos noventa y nueve libros menores, pero distintos. Es decir, lo que nos parece una deficiencia -no todas las obras son tan buenas como la Ilíada- en realidad es un enriquecimiento, porque así hay una diversidad que de otro modo no existiría (Savater, 2008, p. 111).
Estudiemos otra analogía que se ha elaborado con base en Rawls (2006). Lo anterior se puede comparar con la idea de permitir la existencia de multimillonarios en sociedades donde hay pobreza, injusticia social y desigualdad. Aunque parezca contraintuitivo, es bueno permitir que existan personas muy adineradas porque esto genera más movimiento económico y la economía podría desarrollarse de modo conveniente si no para todos al menos sí para la gran mayoría. En un país donde no hay este tipo de personas, no hay quien invierta el capital suficiente como para hacer rodar la economía hacia el progreso. En cambio, en países donde se permite el libre mercado, el avance económico es posible hasta cierto punto. Análogamente, Leibniz razona que si no existiera un poco de mal, no se podría dar toda la variedad existente en comparación con otros mundos donde no existe el mal. Por eso, existe el mal en este mundo. Esta solución, sin embargo, es discutible y los alumnos podrían aceptar como no aceptar esta idea. El objetivo es provocar la discusión y el intercambio de puntos de vista. Enseguida, se analiza la paradoja de los viajes en el tiempo.
Paradoja de los viajes en el tiempo
Esta paradoja (a la cual también se le conoce como la paradoja del abuelo) fue planteada en la novela Le Voyageur Imprudent de René Barjavel (1944) y puede ser utilizada para discutir la naturaleza del tiempo con estudiantes de física o de filosofía. Imaginemos que una persona viaja en el tiempo hacia el pasado. Ahora bien, este viajero de modo involuntario termina matando a su propio abuelo. Esto genera un problema porque si el abuelo no vivió, entonces su padre tampoco y, en consecuencia, el viajero tampoco existiría. Pero si dicho viajero no existió, entonces tal viaje no se hizo, el abuelo siguió con vida, engendró al padre del viajero el cual, a su vez, engendró al viajero mismo. Luego, este viajero visitaría el pasado y mataría a su abuelo y así continúa la paradoja.
El asunto se relaciona con la idea que tenemos del tiempo. El tiempo puede ser concebido como lineal o circular. Esta interpretación es cultural, aunque, desde la Ilustración, Occidente asume que el tiempo avanza hacia adelante marcando la senda del progreso. Con respecto a la paradoja, podría decirse que una vez que el viajero mata al abuelo, él no tendría por qué verse afectado, ya que se habría creado otra línea temporal donde efectivamente él no ha nacido, pero no se trata del mismo viajero, sino de su versión en esa nueva línea del tiempo recién creada. Esta cuestión entonces implica abrir la mente a ideas tales como líneas temporales alternas y mundos posibles. Precisamente, esta es la tendencia de las últimas películas de ciencia ficción como Avengers: Endgame del 2019 y Everything Everywhere All at Once del 2022. El tema de los mundos posibles, a su vez, puede llevar a revisar nociones básicas de lógica modal. Y la idea de líneas temporales alternas nos permite pensar acerca de si los hechos históricos acontecen de forma necesaria o de forma contingente. Si los hechos históricos son necesarios, entonces no existen líneas temporales alternas; pero si se asume que los hechos históricos son contingentes, eso significa que pueden acontecer como no acontecer. Y la discusión puede continuar. A continuación, se analizará la paradoja del huevo y la gallina.
Paradoja del huevo y la gallina
Esta paradoja aparece en la cuestión III del libro II de las Charlas de Sobremesa de Plutarco (1987) y plantea la dificultad de decidir el origen de algo. Se dice que de un huevo salen gallinas y que también las gallinas producen huevos. Y esto genera un círculo vicioso, porque dejaría sin explicación la idea de si fue primero el huevo o la gallina.
Al respecto se podría considerar la teoría del acto y la potencia de Aristóteles (trad. en 1994) para intentar evaluar la cuestión de cierto modo. Según el filósofo, el movimiento es el paso del acto a la potencia. Por ejemplo, cuando una semilla crece y se vuelve una planta, podemos decir que en la semilla se actualizó la potencia de “ser planta” y así alcanzó su perfección (entelequia). Ahora bien, en relación con la paradoja podemos afirmar que en el huevo existe la potencia de “ser gallina” con la cual alcanzaría su perfección. En ese sentido, el huevo sería primero porque si bien es cierto que el huevo se convierte en gallina, no es cierto que la gallina se convierta en huevo. La gallina produce huevos, que es muy diferente. Sin embargo, Aristóteles también planteó ideas metafísicas controversiales. Por ejemplo, afirmó que lo que es primero en el tiempo a nivel físico, no es primero en el ser a nivel metafísico. Así, se puede constatar que existe una preminencia de lo intelectivo sobre lo sensible porque lo primero al ser inmaterial no se corrompe ni es contingente. En este punto se puede notar la influencia de su maestro Platón. Aristóteles afirma que para que el niño se convierta en hombre, debe existir de alguna manera la potencia “ser hombre” como una capacidad previa, como una especie de plan a seguir. Desde este punto de vista, la potencia “ser gallina” sería lo primero. Como vemos dentro de la teoría del acto y la potencia de Aristóteles, la cuestión queda indecisa.
No obstante, podemos sugerirles a los alumnos que investiguen por su cuenta teorías biológicas actualizadas para que puedan emitir una opinión con fundamentos, con respaldo científico y no solo sobre la base de especulaciones libres, aunque interesantes. Por ejemplo, desde la biología evolutiva se puede afirmar que la gallina, en tanto ave, proviene de los reptiles. Y, además, los reptiles en su gran mayoría se reproducen mediante huevos. Con el transcurrir de cientos o miles de años, uno de esos huevos generó una protogallina, que al engendrar produjo otro huevo, del cual, mediante sucesivos procesos de reproducción a lo largo de otros cientos o miles de años, emergió una gallina tal y como hoy la conocemos. Si esto fuera cierto, el huevo sería primero. Pero recordemos que la ciencia está en constante proceso de autocorrección. Así que en el futuro esto podría cambiar. Por ese motivo, urge siempre estar actualizado al respecto del avance de la ciencia. Enseguida, conoceremos algunas paradojas geométricas relacionadas con los fractales.
Paradojas geométricas. Fractales
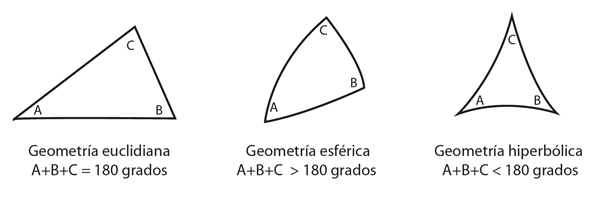
La geometría es aquella parte de la matemática que estudia el espacio. Existen muchos teoremas geométricos conocidos. En especial, son bien conocidos los que tratan sobre triángulos. Por ejemplo, el teorema de Pitágoras es particularmente famoso. Sin embargo, hay una propiedad que es muy reconocida por los estudiantes, a saber, que la suma de ángulos internos de un triángulo equivale a 180 grados.
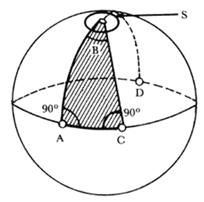
El asunto es que esta verdad es aceptable hasta cierto punto pues existen otras geometrías donde la suma, incluso, puede ser más. Pensemos en una esfera. Fijémonos en el ecuador y en el triángulo que se forman gracias a los meridianos que salen de un mismo polo como en la siguiente imagen.
Es evidente que los ángulos que hacen los meridianos con el ecuador son de 90 grados y si le agregamos el ángulo B de la parte superior, tendríamos un triángulo cuya suma de ángulos es más que 180 grados. A esta geometría se le llama “esférica”. Pero existe también otra denominada “hiperbólica”, donde la suma de ángulos internos es menor que 180 grados. Veamos la siguiente imagen.
Entonces, ante la pregunta ¿cuánto suman los ángulos internos de un triángulo? La respuesta debe ser: “depende de en qué geometría nos estamos ubicando”.
De la misma forma, la cuestión acerca de cuántas dimensiones tiene una figura depende de la geometría en la que nos ubiquemos. Incluso, la dimensión podría no ser un número entero, como ocurre entre los fractales. Precisamente, la teoría de los fractales fue propuesta por Mandelbrot (1983). Esta es una teoría científica que pretende estudiar los patrones que rigen las fracturas, las rugosidades y las grietas. Escribe Benoît Mandelbrot: “¿Por qué a menudo se describe la geometría como algo “frío” y “seco”? Una de las razones es su incapacidad de describir la forma de una nube, una montaña, una costa o un árbol. Ni las nubes son esféricas, ni las montañas cónicas, ni las costas circulares, ni la corteza es suave, ni tampoco el rayo es rectilíneo” (Mandelbrot, 1983, p. 15). Los fractales son objetos matemáticos cuya estructura básica, irregular o fragmentada, se repite a escalas diferentes. Tienen los siguientes rasgos: son muy irregulares, son autosimilares y sus dimensiones vienen dadas por números fraccionarios.
Enseguida, se presentarán tres fractales y se analizarán sus aspectos paradójicos. Sin embargo, es importante advertir que el aspecto controversial de estas figuras desaparece cuando se comprende que forman parte del marco teórico de una geometría totalmente diferente a la usual.
Polvo de Cantor
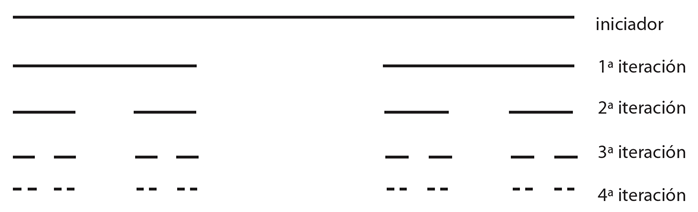
El polvo de Cantor se construye de acuerdo con los siguientes pasos:
Primer paso. Sea una línea que luego ha de ser partida en tres. Enseguida, se borra el segmento central. Esta es la primera iteración.
Segundo paso. Dividamos en tres los otros segmentos y borremos la parte media de cada uno de los dos segmentos. Esta es la segunda iteración.
Tercer paso. Hagamos lo mismo con los siguientes segmentos restantes hasta el infinito.
La figura resultante de aplicar el anterior proceso infinitas veces es el polvo de Cantor. El problema con esta figura radica en ubicarlo en su espacio geométrico. ¿Cuántas dimensiones tiene? No es un punto, tampoco una recta, menos una figura. ¿Qué es? Se trata de un tipo de figura que corresponde a un fractal. Un fractal es un constructo geométrico cuyas dimensiones no están dadas por números enteros, sino más bien por números fraccionarios. La dimensión de esta figura está entre 0 y 1, esto es, 0.6309297.
Triángulo de Sierpinski
Este triángulo se construye siguiendo estos pasos:
Primer paso. Partimos de un triángulo equilátero normal. Ya que el lado es 2, su perímetro es 6. Además, sabemos que el área de la región sombreada con color negro de esta figura es ya que la fórmula para encontrar el área de un triángulo equilátero es (es decir, lado al cuadrado por entre 4).
Segundo paso. Enseguida, dividimos su área en cuatro borrando el pedazo de área del centro. El perímetro de los 3 triángulos ahora es: 3.3 = 9. Asimismo, puesto que se ha dividido entre 4 y, además, nos hemos quedado con 3 pedazos, el área de la región sombreada es igual a 3/4 .
Tercer paso. Volvemos a aplicar este proceso, es decir, dividimos cada triángulo en cuatro partes y borramos el pedazo de área central. El perímetro de los 9 triángulos será: 3.3.3 (1/2) = 27/2. Mientras, debido a que se ha dividido entre 16 y, además, nos hemos quedado con 9 pedazos, el área de la región sombreada es (3/4)2 .
Cuarto paso. Seguimos aplicando este proceso y obtenemos los siguientes resultados. El perímetro de los 27 triángulos sigue aumentando y es: 3.3.3.3.(1/4) = 81/4. Y su área, con base en consideraciones similares a las anteriores, es igual a (3/4)3
Quinto paso. En esta quinta fase aplicamos lo mismo. El nuevo perímetro es: 243/8 y el área será (3/4)4
Como se puede apreciar, este fractal manifiesta una relación poco común entre el área y su perímetro. Mientras que el perímetro tiende hacia el infinito, el área tiende a ser cero. En la geometría euclidiana suele suceder que una figura con un área infinita tiene un perímetro infinito y, a su vez, una figura con perímetro infinito tiene área infinita. Además, una figura con área igual a cero, no debería tener existencia gráfica, lo cual no sucede con el triángulo de Sierpinski. Asimismo, una figura con perímetro igual a infinito tiene por medidas de sus lados al infinito o bien tiene infinitos lados. Pero, en el triángulo analizado sucede que tan solo se ven acumulaciones de puntos por doquier. La dimensión fractal de este objeto es 1.58496.
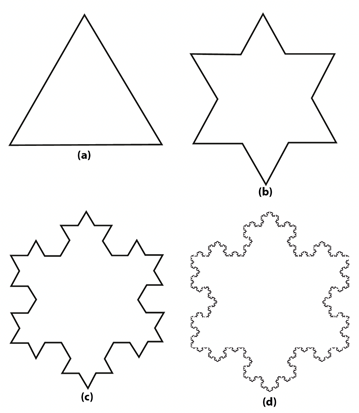
Copo de nieve de Koch
Esta figura se construye del siguiente modo:
Primer paso. Comencemos analizando el perímetro de la imagen (a) de la figura 10 que representa un triángulo equilátero. Si cada lado es igual a 1, su perímetro será 3. El área vale ()/4 y esto lo sabemos al aplicar la fórmula para triángulos equiláteros.
Segundo paso. Dividamos cada lado en 3 partes y sobre las partes medias construyamos otros triángulos equiláteros como en la imagen (b). Se han agregado 6 segmentos de 1/3, pero hemos borrado 3 segmentos de 1/3. En total hemos aumentado 3 segmentos de 1/3. El nuevo perímetro es: 3 + 1. Dado que se han agregado tres nuevos triángulos equiláteros cuyos lados valen 1/3, la nueva área ahora vale ()/4 + ()/12
Tercer paso. Volvamos a repetir el proceso. Comenzamos dividiendo en 3 partes esos segmentos de 1/3 y luego hacemos todo lo demás. Al final hemos de aumentar 24 segmentos de 1/9, pero también borramos 12 segmentos de 1/9. En total hemos aumentado 12 segmentos de 1/9, o sea 4/3. El nuevo perímetro es: 3 + 1 + 4/3. Debido a que se han agregado doce nuevos triángulos equiláteros cuyos lados valen 1/9, la nueva área ahora vale ()/4 + ()/12+ ()/27.
Cuarto paso. Nuevamente, volvemos a realizar todo este procedimiento. El perímetro sería igual a: 3 + 1 + 4/3 + (4/3)2. Y si continuamos así, este proceso repetido infinitas veces dará como resultado el aumento constante de una nueva potencia de (4/3). Tendremos, por ello, una figura cuyo perímetro es Z.
Z = 3+1+4/3+(4/3)2+(4/3)3+(4/3)4+ …
Pues bien, Z forzosamente tiende a ser infinito. Pero gráficamente observamos su finitud. Por otro lado, el área A mide
A= ()/4 + ()/12+ ()/27 + …
Esto significa que tiende a ser finito, aunque pequeño. Esta cantidad no pasa de 0.7 y, es 0.6928 aproximadamente. Por ello, esta figura conserva ciertas propiedades de las figuras planas como la finitud del área, pero distorsiona otras como la infinitud de su perímetro.
Todas las figuras planas de dos dimensiones tienen un perímetro finito porque están limitadas por líneas cerradas. Sin embargo, la figura analizada tiene un perímetro infinito a pesar de que gráficamente es posible detectar su finitud. Con lo anterior demostramos que este copo de nieve rompe con la unidimensionalidad, puesto que se proyecta hasta el infinito superando los segmentos de recta. Pero en el plano de la bidimensionalidad se sigue respetando la finitud del área de los polígonos cerrados. Por ello, esta figura del copo de nieve, en realidad, es un fractal cuya dimensión es más que la de la línea (metros) y menos que la del plano (metros cuadrados), es decir, está entre 1 y 2. Exactamente, su dimensión es 1.26186. Ahora, se discutirá acerca de lo que siente un estudiante cuando se ubica ante estas paradojas.
¿Qué siente un estudiante ante las paradojas?
Cuando un estudiante comprende la auténtica y tétrica naturaleza problemática de una paradoja, se asombra, pero es posible que sienta algo de vértigo. Se vuelve a repetir la misma sensación que experimentan cuando ven una serie muy interesante y, de pronto, el protagonista triunfante y heroico es atravesado por una filosa espada que el antagonista alcanza a usar con su último aliento.
“¡Ahhh! … ¡Ohhh! … ¿Qué?...”. Los alumnos sorprendidos suelen expresarse de manera emotiva y afectiva ante estos grandes problemas. Incluso, puede parecer que las paradojas los asustan o que los fastidian. Esa es la idea. Una clase no puede convertirse en la exposición de una lista de saberes o de conocimientos que el docente fríamente transmite a sus pupilos. En realidad, una buena sesión educativa debería motivarlos para que ellos, por su cuenta, puedan seguir investigando. Y esta consideración implica que el docente debe enseñar transmitiendo valores, es decir, con cariño, amor, respeto, cuidado y diligencia. Al mismo tiempo, hay que mantener la autoridad en el aula tratando de que se den cuenta de que ellos, los pupilos, están ante un hombre o una mujer de cultura. Desde esta perspectiva, los docentes son guardianes de la cultura y el pensamiento.
El maestro debe estar preparado. La educación brindada debe basarse en estrategias para que los conceptos básicos del estudiante puedan “artificialmente” entrar en crisis. El docente debe dosificar el uso de estas potentes paradojas para que el pupilo pueda aprender que incluso lo más seguro del mundo cae ante el poderoso peso del pensamiento crítico. Los profesores deben ayudarles a derrotar al desánimo, al miedo, a la falta de libertad, al qué dirán, al abuso y, en fin, a todo aquello que ponga en peligro nuestra humanidad. Esto muestra que en el proceso educativo se ponen en juego tanto el razonamiento como la inteligencia emocional (Bravo y Urquizo, 2016).
El estudiante debe sentir que aprender es algo bonito. Debe sentirse desafiado no tanto por el docente como sí por su propia mente. Es necesario que el profesor pueda dominar el uso de las paradojas como recursos didácticos ante la situación actual de nuestra educación. Debido a esta lamentable situación, el estudiante asume que ir a la escuela prácticamente no lo ayuda a conseguir sus metas más prácticas para poder incorporarse a la realidad laboral. Las paradojas pueden servir como apoyo para mejorar la realidad educativa. Ha llegado el momento de que desaparezca esa vieja manera de enseñar que aleja a los estudiantes de la discusión, la polémica, el debate y las ansias por querer saber más cada día.
Conclusiones
En este artículo se han considerado las paradojas como recursos didácticos. Así, se aclararon los conceptos de falacia y reducción al absurdo pues las paradojas han sido vistas como falacias muy sutiles por algunos estudiosos y, además, hay quienes utilizan las paradojas para realizar deducciones como ocurre en la reducción al absurdo.
Enseguida se analiza una lista de paradojas, pero con el objeto de que puedan ser utilizadas en un aula de clase. Así, se trata sobre algunas paradojas tales como la paradoja de Aquiles y la Tortuga, la paradoja de Galileo, la paradoja del hotel de Hilbert, la paradoja de Tristam Shandy, la paradoja de Protágoras, la paradoja de Monty Hall, la paradoja de Dios y la piedra, la paradoja de Epicuro, la paradoja de los viajes en el tiempo, la paradoja del huevo y la gallina y algunas paradojas geométricas relacionadas a los fractales.
Se ha finalizado esta investigación tratando de explicitar el aspecto afectivo y emocional que un estudiante experimenta cuando trata con esta clase de problemas, es decir, se trata de explicar qué es lo que siente un estudiante cuando su profesor o profesora le presenta una paradoja.
Ahora bien, hemos encontrado hallazgos así como limitaciones en este trabajo. Empezaremos por las limitaciones. Esta investigación tiene algunas dificultades. En primer lugar, los profesores tendrían que desarrollar constantemente trabajos académicos para encontrar paradojas y así difundirlas en sus diferentes clases. En segundo lugar, las paradojas que se han seleccionado en este trabajo, de alguna manera ya han sido conocidas en otros ámbitos académicos y, en ese sentido, no representan novedad alguna. Finalmente, en tercer lugar, el hecho de que existan tantas paradojas podría cultivar en los alumnos una perspectiva escéptica acerca de la realidad y el conocimiento de tal modo que opten por guardar silencio antes que seguir indagando.
Para terminar señalaremos los logros de este escrito. Este trabajo ha buscado revelar el aspecto educativo y didáctico de las paradojas. Se recomienda que se aproveche didácticamente el problema generado por el hallazgo y la exposición de una paradoja. Lo cierto es que las paradojas pueden ser aliadas en el proceso de enseñanza-aprendizaje y su uso puede beneficiar a la actividad educativa. La enseñanza que las paradojas nos dejan es muy valiosa, pues revela que lo que llamamos “conocimiento” es algo que siempre puede ser ampliado constantemente. Las paradojas poseen valor propedéutico y, en tanto problemas que llaman la atención, enseñan que existen límites en nuestra comprensión de algún fenómeno.
El modo de aprender a través de paradojas implica tratar de resolver los desafíos mentales planteados. Con las paradojas, los alumnos de cualquier carrera pueden pensar de forma adecuada sobre los conceptos fundamentales de su misma especialidad. Así, la educación brindada debe basarse en estrategias para que los conceptos básicos del estudiante puedan “artificialmente” entrar en crisis. Con las paradojas, el pupilo aprende que incluso lo más seguro del mundo cae ante el poderoso peso del pensamiento crítico. Las propuestas de solución (o disolución) que inspiran las paradojas son discutibles y los alumnos podrían aceptarlas como rechazarlas, precisamente, el objetivo es provocar la discusión y el intercambio de puntos de vista. Este el asunto. Ante las paradojas uno siente ganas de hablar, de opinar o al menos de pensar la cuestión con detenimiento.
Si no se llega a una respuesta, el docente puede comprometer a que los alumnos investiguen por su cuenta teorías actualizadas para que puedan emitir una opinión con fundamentos, con respaldo científico y no solo sobre la base de especulaciones. Una clase no puede convertirse en la exposición de una lista de saberes o de conocimientos que el docente fríamente transmite a sus pupilos. En realidad, una buena sesión educativa debería motivar a los alumnos para que ellos, por su cuenta, puedan seguir investigando con el fin de que sepan más sobre la cuestión planteada. Los profesores deben ayudarles a derrotar al desánimo, al miedo, a la falta de libertad, al qué dirán, al abuso y, en fin, a todo aquello que ponga en peligro nuestra humanidad. Y el camino de la investigación es un buen sendero para ejercitar nuestra libertad sin miedo y con ganas de saber cada vez más.
Cuando un estudiante comprende la auténtica y tétrica naturaleza problemática de una paradoja, se asombra de una forma muy parecida a la que experimentaron los primeros filósofos al ver el orden y el caos que exhibe el mundo. Los alumnos sorprendidos suelen expresarse de manera emotiva y afectiva ante estos grandes problemas. Cuando conocen el reto planteado por una paradoja, se genera cierta preocupación de su parte. La aceptación de estos retos hará del alumno alguien más preparado para la toma de decisiones en su vida diaria, pues habrá ejercitado de modo conveniente el pensamiento crítico. Asimismo, una paradoja nos enseña lo que desconocemos, nos hace conscientes de nuestros límites. En ese sentido, nos vuelve más humildes. El estudiante debe sentir que aprender es algo revitalizante. La vida no debe ser olvidada durante el proceso de enseñanza-aprendizaje. El pupilo debe sentirse desafiado no tanto por el docente como sí por su propia mente.