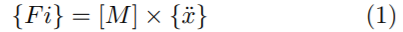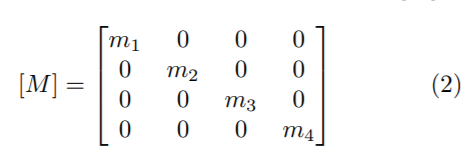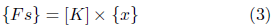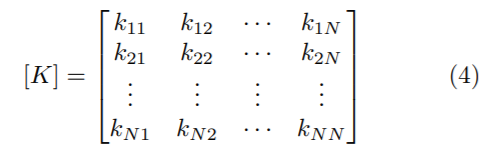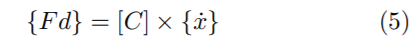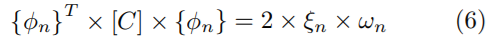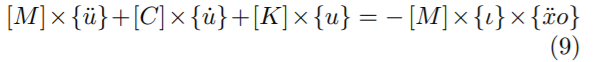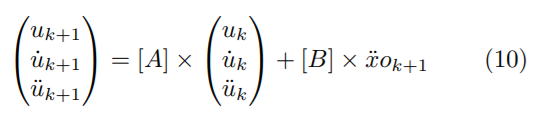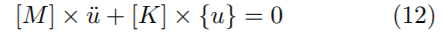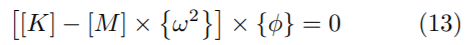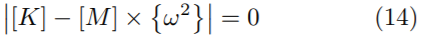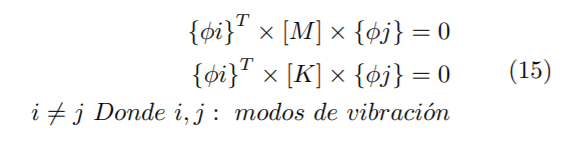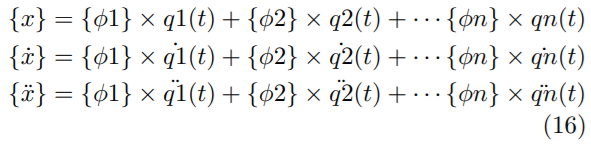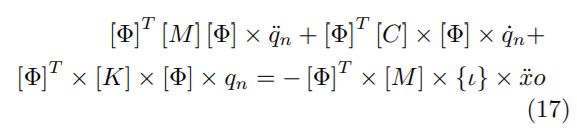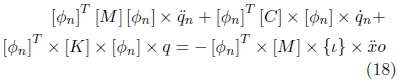Forma sugerida de citación
Tapia Andrade, A. y Torres Berni, W. (2021). «Evaluación de las propiedades dinámicas de un pórtico plano (MDOF) en una mesa vibratoria». Ingenius. N.◦ 26, (julio-diciembre). pp. 49-62. doi: https: //doi.org/10.17163/ings.n26.2021.05
1. Introducción
Ecuador tiene una actividad sísmica considerable, el último sismo que afectó en gran intensidad al país ocurrió el 16 de abril de 2016 con una magnitud de momento Mw 7.8, sucedió en las provincias costeras de Manabí y Esmeraldas [1], dejando daños materiales, colapsos en edificaciones y cerca de setecientos muertos.
El terremoto se originó debido a la subducción de la placa oceánica de Nazca por debajo de la placa sudamericana; el rozamiento entre ambas placas produce acumulación de energía elástica, la cual se relaja cuando existe una ruptura súbita y se produce el evento sísmico [2].
Esto ha motivado a los ingenieros a desarrollar una filosofía que se centre en impedir la pérdida de vidas, controlando el colapso de todas las estructuras [3]. Por lo cual toda edificación debe ser diseñada considerando la solicitación sísmica; el análisis de la estructura frente a este tipo de carga es el principal problema que intenta resolver la dinámica estructural.
En la mayoría de los casos, el estudio de la dinámica estructural se lo realiza de manera teórica, sin poder observar físicamente el comportamiento de las estructuras ante un sismo o aceleración en la base. Por lo cual este proyecto se centra en construir modelos experimentales de múltiples grados de libertad con materiales apropiados, eso significa losas muy rígidas comparadas con los pilares a flexión, donde el modelo va a concentrar la deformación de la estructura. Además, tanto los pilares como los pisos se consideran axialmente rígidos, en el modelo analítico, se va a considerar que los pisos concentran la masa, y que los parantes son quienes colaboren con la rigidez, es decir, que se comporte como un edificio a corte [4].
Para obtener respuestas dinámicas y propiedades modales en modelos experimentales y estructuras reales se han implementado técnicas experimentales, como la colocación de acelerómetros triaxiales, o la utilización de equipos de excitación dinámicas que reproducen sismos a escala [5]. En el proyecto se utilizó una mesa vibratoria, conocida como Shake Table II [6]. Este dispositivo es un simulador de terremotos para modelos físicos académicos pequeños (masa máxima = 7,5 kg), que permitirá generar aceleraciones de piso en forma de pulsaciones, barridos sinusoidales y registros sísmicos (escalados) [6]. La Shake Table II permite reproducir aceleraciones de piso en dos direcciones (x, y), sin embargo, para el proyecto se trabajó con modelos planos, se utilizó aceleración unidireccional, cada piso solo se moverá en una dirección [7].
En [8, 9] y [10] se han determinado propiedades dinámicas de estructuras experimentales con el mismo método, sin embargo, estas se centran solo en desplazamientos máximos y otras solo en la obtención de frecuencias, además, están limitados a dos pisos. En el proyecto se analizará desde la obtención de frecuencias, amortiguamientos y, además, los modelos por su modo de construcción, tienen la posibilidad de apilarse y llegar hasta un modelo de seis pisos, siendo la única limitante, el peso máximo que soporte la mesa vibratoria.
2. Materiales y métodos
En el proyecto consta del sustento teórico, donde se da a conocer los conceptos de la dinámica estructural utilizados para el desarrollo del script en MatLab; y la parte experimental, donde se establece el tipo de material a utilizarse, las características geométricas, la aceleración de la base, la aceleración de cada piso, la operación de la mesa vibratoria, la forma de adquirir respuestas y su procesamiento.
2.1. Sistema de múltiples grados de libertad
Un sistema de múltiples grados de libertad (MDOF) se puede entender desde el punto de vista de la dinámica estructural como aquel que requiere más de una coordenada para describir su movimiento. Los grados de libertad también pueden determinar las direcciones de la aceleración de las masas concentradas. En el proyecto, la dirección del sismo será uniaxial, por lo tanto, el número de grados de libertad, será uno por cada piso [7].
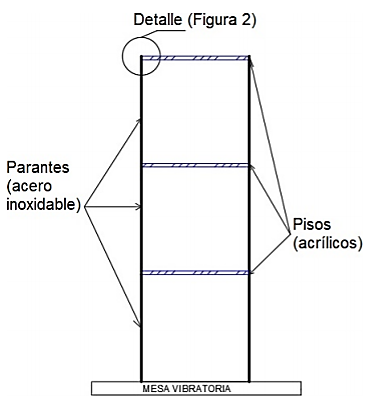
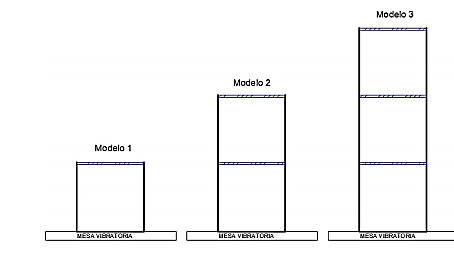
Los modelos experimentales son modulares y pueden llegar a sistemas desde uno hasta seis grados de libertad, los ensayos fueron realizados con los sistemas de uno, dos y tres grados de libertad. En la Figura 1 se muestra el modelo de tres grados de libertad.
2.2. Edificio a cortante
Un edificio a cortante se caracteriza como un arreglo que concentra la masa en cada piso, además, deben actuar como diafragmas infinitamente rígidos a flexión y carga axial. Por lo tanto, en el modelo, solo las columnas deben colaborar con la rigidez [4].
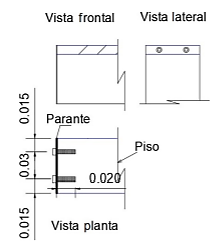
Las consideraciones realizadas anteriormente permiten simplificar la estructura y resolver el problema como un MDOF, donde las losas infinitamente rígidas, permiten asegurar que no existirán rotaciones entre parantes y pisos. En el modelo experimental la rotación se controló en función de la conexión que tiene el parante y el acrílico, ya que la conexión no está fija en un punto, sino en un área como se observa en la Figura 2. En cuanto a la deformación axial, será despreciable, debido a las características físicas de los pisos.
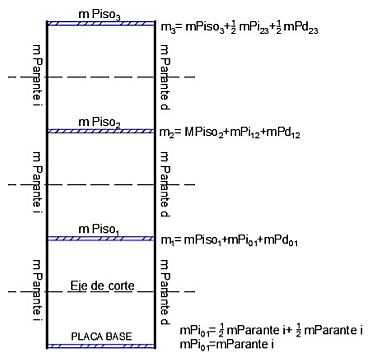
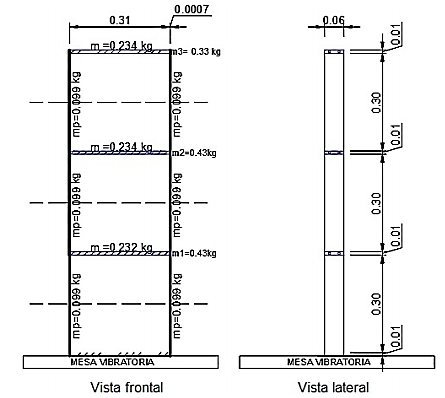
En el modelo experimental, se debe tener en cuenta que las columnas aportan masa, por lo cual se realizó la consideración de que la losa concentra la mitad de la masa de cada columna que esta sobre y bajo de ella, como se muestra en la Figura 3.
Donde: mPiij y mPdij es la masa del parante desde el grado de libertad i hasta el grado de libertad j. Eje de corte: es el que ayuda a cuantificar cómo se concentró la masa de cada piso.
2.3. Fuerza inercial
Relaciona las fuerzas externas que actúan sobre la masade la estructura con las aceleraciones de los grados de libertad dinámicos como se muestra en la Ecuación (1) [11].
Donde {Fi} es el vector de la fuerza de inercial, [M] es matriz de masa y {x} es el vector de aceleración de los grados de libertad.
La matriz de masa (2) es una estimación de la masa de toda la estructura, a esta matriz también se la conoce como «matriz de masa concentrada» [12].
2.4. Fuerza elástica
Relaciona las fuerzas externas sobre la rigidez de la estructura con los desplazamientos de los grados de libertad dinámicos, como se muestra en la Ecuación (3) [11].
Donde {F s} es el vector de la fuerza elástica, [K] es matriz de rigidez y {x} es el vector de desplazamiento de los grados de libertad.
La matriz de rigidez (4) incluye propiedades de las columnas, como son la longitud, área y módulo de elasticidad [12].
2.5. Fuerza de amortiguamiento
Es un mecanismo con el cual se puede disipar energía de la estructura, según esto se relacionan las fuerzas externas que actúan sobre el amortiguamiento con las velocidades de los grados de libertad dinámicos como se muestra en la Ecuación (5) [11].
Donde {F d} es el vector de la fuerza de amortiguamiento, [C] es matriz de amortiguamiento y {x˙} es el vector de velocidad de los grados de libertad.
Para la obtención de la matriz de amortiguamiento se va a suponer amortiguamiento clásico. La matriz de amortiguamiento clásico se puede utilizar en este tipo de modelos, si los mecanismos de amortiguación son similares en toda la estructura, es decir, una estructura que sea de MDOF y que a su vez esté conformada por un mismo sistema estructural y materiales similares, en toda la altura [11].
Uno de los procedimientos dentro del amortiguamiento clásico es el amortiguamiento modal. El análisis provee el amortiguamiento de un número específico de modos, como se indica en la Ecuación (6) [13] y [14].
Donde C es matriz de amortiguamiento, φn es el vector de cada forma modal, ξn es el factor de amortiguamiento, ωn frecuencia natural, y n es número de modos.
2.5.1. Factor de amortiguamiento
Una característica importante es el amortiguamiento de la estructura, el cual queda definido con base en el factor de amortiguamiento, por esta razón hace falta obtenerlo aplicando el método del ancho de banda descrito a continuación [15].
a) Ancho de banda
Se trata de un método para la obtención del factor de amortiguamiento en el dominio de la frecuencia; esta técnica es ampliamente utilizada en la práctica profesional, en la cual una estructura debe ser excitada por pulsaciones simultáneas o individuales a diferentes frecuencias [16].
Con el fin de aplicar el método se debe considerar el efecto del movimiento de la base, por lo cual se procede a encontrar el cociente entre las amplitudes de la transformada de Fourier de los registros de aceleración de cada losa con respecto a los registros de la base. A esto se lo conoce como transmisibilidad [11], la cual se indica en la Ecuación (7).
Donde T r es transmisibilidad, αo(ω) amplitud de la aceleración de cada piso en el dominio de la frecuencia y αb(ω) amplitud de la aceleración de la base en el dominio de la frecuencia.
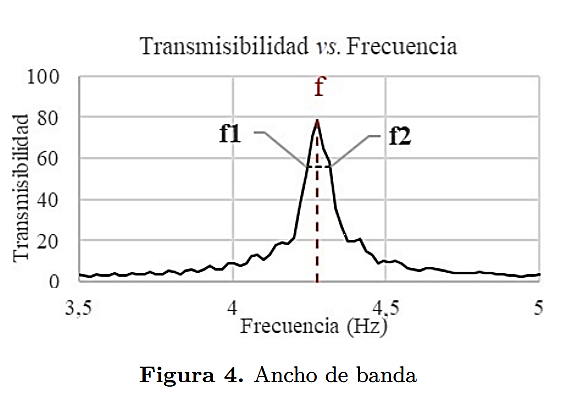
A partir del cálculo de la transmisibilidad se obtienen gráficas respecto de la frecuencia y el factor de amortiguamiento se determina mediante la diferencia entre dos frecuencias llamadas puntos de media potencia sobre la frecuencia correspondiente de cada modo. Los puntos de media potencia son las frecuencias que se encuentran a 1/√2 de la amplitud máxima de la transmisibilidad, como se indica en la Figura 4, y esto permitirá aplicar la Ecuación (8) [17].
Donde f es la frecuencia con amplitud máxima (Hz), f1 y f2 son las frecuencias de media potencia (Hz).
2.6. Ecuación del movimiento
Con base en las fuerzas detalladas en las secciones anteriores, se establecerá la ecuación del sistema MDOF, tomándose en cuenta la segunda ley del movimiento de Newton, se obtiene la Ecuación (9).
Donde {ι} es el vector de colocación, {xo¨ } la aceleración de piso para cada instante de tiempo y u es la coordenada relativa de cada grado de libertad respecto de la base.
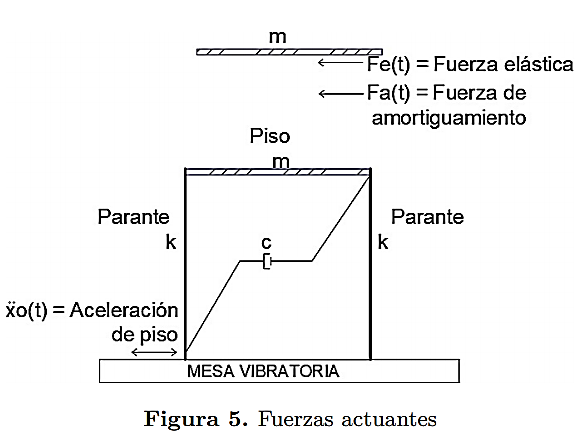
En la Figura 5 se presentan las fuerzas actuantes, sobre el sistema
2.7. Método de Newmark
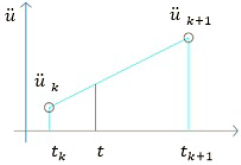
Es un método muy versátil, para el cálculo de la respuesta un sistema dinámico. En 1959, N. M. Newmark desarrolló una familia de métodos dependiendo de la ley de variación entre instantes consecutivos de tiempo [11]; el que se utilizó es el de aceleración lineal como se muestra en la Figura 6.
La representación matricial del método aplicado para la obtención de las respuestas de aceleración, velocidad y posición en el tiempo para un sistema de un grado de libertad, se muestra en la Ecuación (10), donde la respuesta en instante k + 1, solo depende dela respuesta del instante k[11].
Donde [A], [B] son matrices de constantes que dependen de la frecuencia, amortiguamiento, rigidez e intervalo de tiempo y xo¨ k+1 es aceleración de piso en el instante k + 1 [12] y [18].
2.7.1. Estabilidad del método
Existen dos tipos de métodos dependiendo de la estabilidad de los mismos: condicionalmente estables e incondicionalmente estables [11].
Los procedimientos condicionalmente estables dependen del paso del tiempo y los procedimientos incondicionalmente estables son independientes del paso del tiempo [11]
El método de Newmark con base en la aceleración lineal es condicionalmente estable y debe cumplir con la Ecuación (11), para poder ser aplicado.
Donde At es el intervalo de tiempo y T es el periodo del sistema.
2.8. Análisis modal
Permite calcular la respuesta de la estructura con base en los modos de vibración. Para ello es importante definir sus propiedades dinámicas: frecuencia, amortiguamiento y formas modales para cada modo [19].
Este análisis es muy útil porque permite descomponer las respuestas de una estructura en modelos de un solo grado de libertad y al combinarlas obtener la respuesta del sistema MDOF
2.8.1. Frecuencias y modos de vibración
En el sistema amortiguado de múltiples grados de libertad, se debe establecer las frecuencias naturales y las formas modales considerándolo como si se tratase de un sistema sujeto a vibración libre y sin amortiguamiento, por lo cual en la Ecuación (9), los términos de la aceleración de piso y amortiguamiento se anulan, y se obtiene la Ecuación (12).
Resolviendo esta ecuación diferencial se llega a la Ecuación (13), la cual es la base para la resolución del problema de valores y vectores propios [11].
La Ecuación (13) corresponde a un sistema de ecuaciones simultáneas homogéneas, por definición solo tiene solución no trivial, por tanto, el determinante de la matriz de coeficientes es cero, como se indica en la Ecuación (14) [20].
Al expandir el determinante se obtiene un polinomio de orden 2n (n: número de modos de vibración), donde ω 2 es la variable. Esta ecuación se la conoce como «ecuación de frecuencias». Las soluciones se denominan valores propios y las raíces cuadradas de estas, corresponde a las frecuencias naturales del sistema ω[21].
Para determinar los vectores propios o modos de vibración φ, se sustituye las frecuencias naturales ω en la Ecuación (13) y se resuelve.
2.8.2. Ortogonalidad de los modos
El análisis anterior permite demostrar que los modos de vibración de diferentes frecuencias, cumplen la condición de ortogonalidad, que se muestra a continuación (15) [11].
Donde φi y φj son formas modales para los modos i y j, [M] matriz de masa y [K] matriz de rigidez.
A partir de ello, se obtiene que el sistema se puede resolver para cada modo de vibración como un sistema separado sin influencia de un modo con respecto al otro, y la respuesta del sistema completo se define con base en la Ecuación (16).
Donde φi forma modal, y q, q˙ y q¨ son las coordenadas modales de posición, velocidad y aceleración, en el modo i-simo.
Reemplazando la respuesta {x}, {x˙} y x¨ con base en la suma de los modos y premultiplicando por la matriz de formas modales transpuestas, se obtiene la ecuación (17).
Basándose en la Ecuación (17) y la propiedad deortogonalidad, se puede definir la Ecuación (18) paracada modo de vibración.
A partir de la Ecuación (18) y con ayuda del método Newmark de aceleración lineal, se obtiene respuestas dinámicas relativas (posición, velocidad y aceleración) en cada instante de tiempo para cada coordenada modal.
2.9. Diseño del programa
2.9.1. Lenguaje del programa MatLab
El programa ATH Dynamic responses ha sido desarrollado en el software Matlab, el cual es un lenguaje de programación con un entorno de trabajo amigable. Permite trabajar en modo consola (tan solo se presenta resultados con base en expresiones planteadas) y en modo rutina (programas cuyos comandos están codificados y permiten realizar programas y grabarlos) [7] y [22].
La característica más importante de Matlab es que permite un manejo directo de vectores y matrices, además que la codificación no es compleja [7].
El proyecto se realizó en modo rutina, debido a que se ejecutó un programa con comandos codificados y se creó un GUIDE, que permitió mejorar la interfaz gráfica para el usuario.
2.9.2. Programa ATH Dynamic responses
El programa ATH Dynamic responses se basa en el método numérico de Newmark considerando aceleración lineal para el cálculo de la respuesta de los sistemas de 1 GDL en el análisis modal.
Dentro del programa se deben ingresar las características geométricas, la rigidez de los parantes y la masa considerada como concentrada en cada piso. Con base en esto se obtienen respuestas dinámicas relativas (posición, velocidad y aceleración) y propiedades modales del modelo físico (frecuencia, modos y porcentaje de masa participativa).
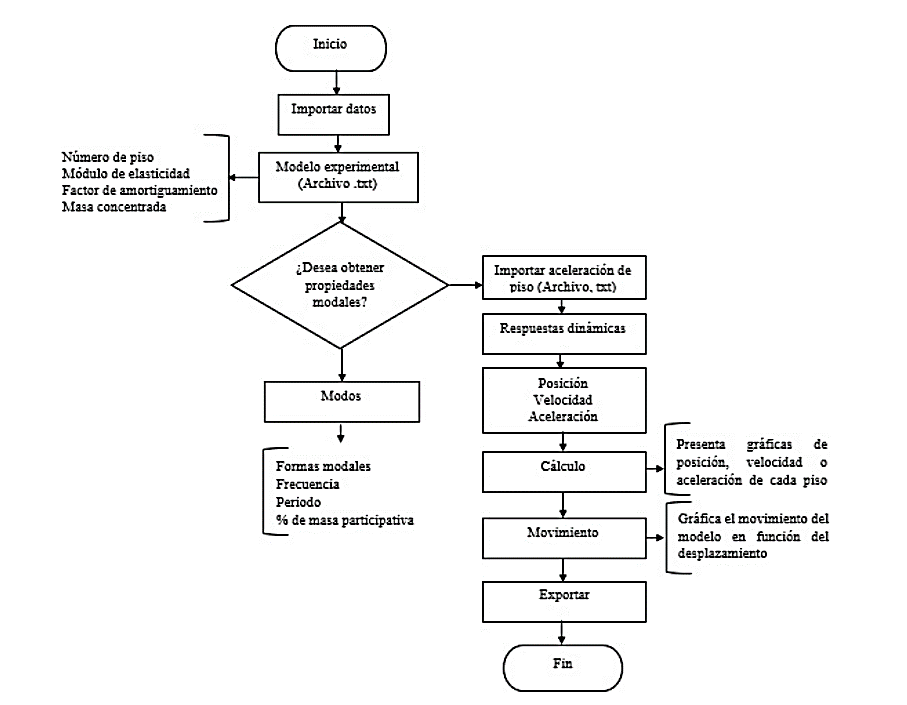
Para comprender la funcionabilidad del programa, en la Figura 7, se indica el diagrama de flujo del mismo.
2.10. Procesamiento de datos
Los datos obtenidos por los acelerómetros necesitan ser corregidos por línea base y filtrado de frecuencias no deseadas. Para lo cual se utilizó el filtro butterworth [23], pasa bajo una frecuencia de corte de 16 Hz. Con este objetivo se ha utilizado el programa AB signal [24].
2.11. Instrumentación
En general, la instrumentación para medir la respuesta dinámica de una estructura, consta de la instalación de sensores que registren respuestas dinámicas (velocidad, aceleración y desplazamiento) [25].
La finalidad de la instrumentación es registrar la respuesta frente al desplazamiento, movimientos internos, sismos y observar el comportamiento de estructuras o modelos [20].
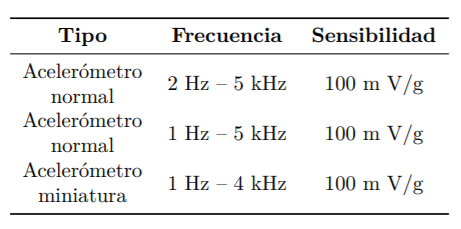
La adquisición de datos del proyecto se efectuó mediante acelerómetros de PCB Piezotronics [25], los cuales tienen frecuencias y sensibilidades que se muestran en la Tabla 1.
2.12. Mesa vibratoria (Shake Table II)
El ensayo en una mesa vibratoria es la forma más directa para simular el comportamiento dinámico de las estructuras. Los modelos estarán limitados a no ser muy pesados, de dimensiones escaladas y no muy rígidos [26].
Shake Table II se desarrolló originalmente por la University Consortium on Instructional Shake Tables (UCIST) [6]. Es un dispositivo mecánico, que consta de una placa superior de 45,7 × 45,7 cm2 donde se ancla el modelo, una placa inferior de 60,9 × 45,7 cm2 y un motor DC con una potencia de 400 W. La mesa soporta una carga de 7,5 kg a una aceleración de 2,5 g y permite movimientos con un recorrido de hasta ±7,62 cm [6].
2.13. Materiales
El equipo utilizado para la realización del proyecto está conformado por una mesa vibratoria Shake Table II [6] y acelerómetros de PCB Piezotronic [25], descritos en la sección 2.11. y 2.12.
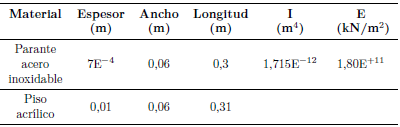
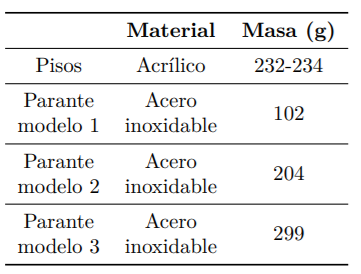
Los modelos experimentales están conformados por acrílicos y acero inoxidable. En las Tablas 2 y 3 se especifican las características y dimensiones de los materiales.
En la Figura 8 se presenta los gráficos de los modelos experimentales que se construyeron. En la Figura 9 se indica las dimensiones del modelo 3 y, además, cómo se realizó la concentración de la masa para el modelo teórico, con base en el modelo experimental y en la Figura 10 se puede observar una imagen del modelo real.
3. Resultados y discusión
Los resultados muestran frecuencias, factores de amortiguamiento, aceleraciones absolutas de los modelos experimentales y su comparación con los resultados teóricos proporcionados por el programa ATH Dynamic responses.
3.1. Experimento 1. Obtención de frecuencias y factores de amortiguamiento de cada modelo
Las frecuencias se obtuvieron de manera teórica mediante el programa ATH Dynamic responses y verificadas con el software SAP2000 [27]. Para la obtención de la frecuencia experimental y el factor de amortiguamiento, se realizó un barrido de frecuencias con la Shake Table II.
Se efectuó el proceso de corrección de línea base y filtrado, como se explicó en la sección 2.10. A partir de ello se utilizó la transformada rápida de Fourier disponible en Matlab [23] y se obtuvo gráficas de transmisibilidad vs. frecuencia como se muestran en las Figuras 11, 12 y 13, donde a la abscisa de cada pico del gráfico le corresponde la frecuencia de cada modo y, además, permite obtener el factor de amortiguamiento aplicando la Ecuación (8). El error porcentual en la frecuencia analítica que se obtuvo es con respecto a la aceleración experimental.
3.1.1. Frecuencias y factor de amortiguamiento del modelo 1
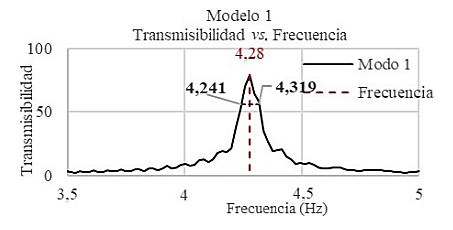
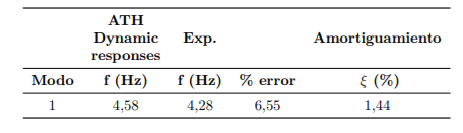
En la Figura 11 se muestran las gráficas que permitieron obtener la frecuencia teórica y el factor de amortiguamiento, y en la Tabla 4 se tabulan estos valores.
El peak de la Figura 11 muestra que la frecuencia experimental para el modelo 1 es 4,28 Hz.
3.1.2. Frecuencias y factor de amortiguamiento del modelo 2
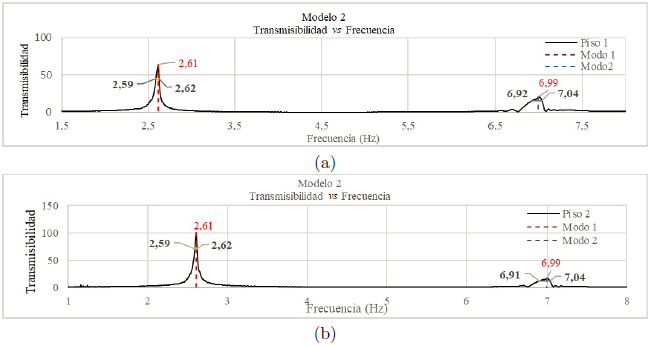
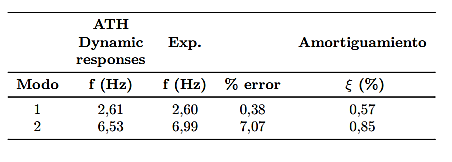
En las Figuras 12 (a) y (b) se muestran las gráficas que permitieron obtener las frecuencias y los factores de amortiguamiento para los dos modos y en la Tabla 5 se presentan los resultados. Los picos de las Figuras 12 (a) y (b) son la frecuencia experimental, para el modo 1 es 2,61 Hz y para el modo 2 es 6,99 Hz.
3.1.3. Frecuencias y factor de amortiguamiento del modelo 3
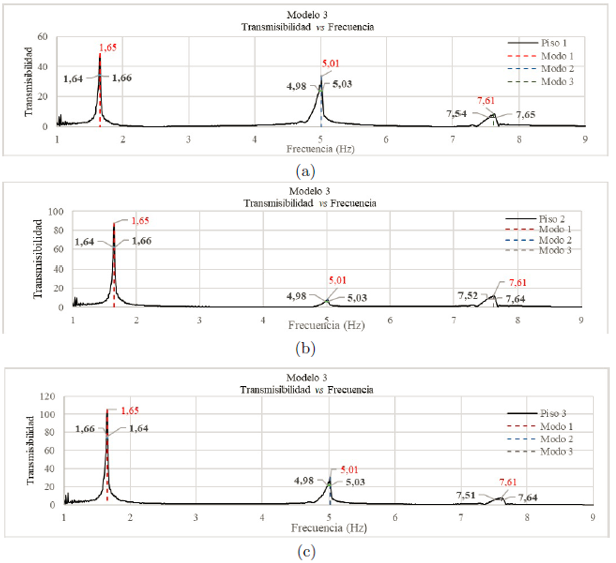
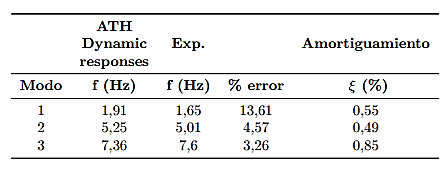
En la Figura 13 (a), (b) y (c) se muestran las gráficas que permitieron obtener las frecuencias, los factores de amortiguamiento para los 3 modos y en la Tabla 6, se presentan los resultados.
Los picos de las Figuras 13 (a), (b) y (c), son las frecuencias experimentales, para el modo 1 es 1,65 Hz, para el modo 2 es 5,01 Hz y para el modo 3 es 7,61 Hz.
3.2. Experimento 2. Respuesta dinámica del modelo a aceleración de piso
La respuesta dinámica se obtuvo al someter a los modelos experimentales a un registro sísmico escalado. El registro sísmico que se utilizó fue El Centro y su escalamiento se realizó mediante el software de la Shake Table II; el escalado del registro fue sobre la base de un desplazamiento máximo de 4 cm.
Los resultados que se presentan a continuación son de aceleraciones absolutas, debido a que estas son las que proporcionan directamente los acelerómetros y se compararon con las aceleraciones absolutas obtenidas del programa ATH Dynamic response, con base en la Ecuación (19):
Donde x¨ es aceleración absoluta, u¨ es aceleración relativa y x¨o aceleración de base.
3.2.1. Modelo 1 registro de aceleración en base: sismo El Centro
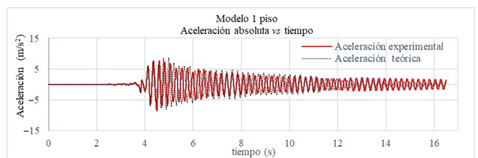
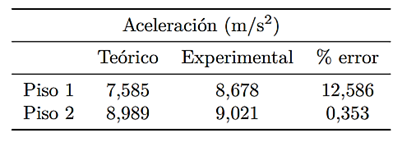
En la Figura 14, se muestra la aceleración experimental y la aceleración teórica del modelo de 1 piso, y en la Tabla 7, las aceleraciones máximas teóricas y experimentales.
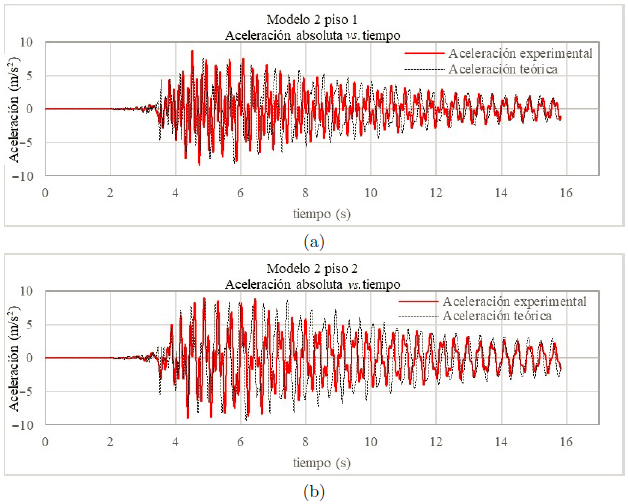
3.2.2. Modelo 2 aceleración base: sismo El Centro
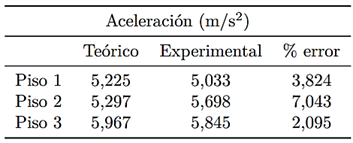
En las Figuras 15 (a) y (b) se muestra la aceleración experimental y la aceleración teórica del modelo 2 y en la Tabla 8 las aceleraciones máximas teóricas y experimentales.
3.2.3. Modelo 3 aceleración base: sismo El Centro
En las Figuras 16 (a), (b) y (c) se muestra la aceleración experimental y la aceleración teórica del modelo 3 y en la Tabla 9 las aceleraciones máximas teóricas y experimentales.
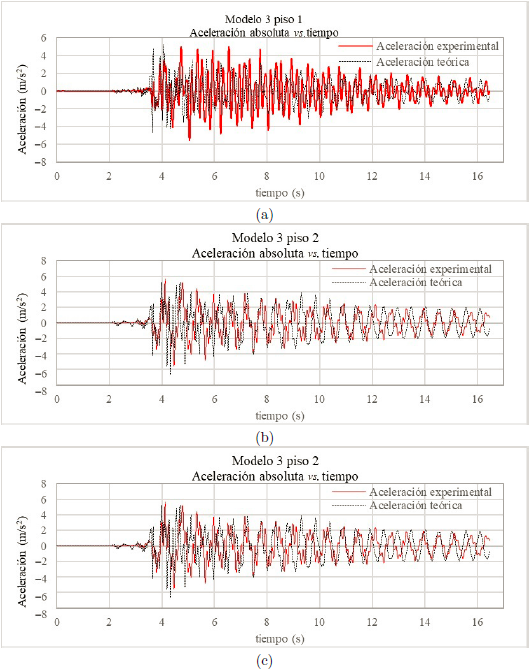
Figura 16. Aceleración absoluta experimental y teórica del modelo 3, con aceleración en la base del sismo El Centro (a) piso 1 (b)piso 2 (c) piso 3
Al comparar gráficamente los modelos, se observó que la aceleración experimental tiene mayor amplitud en la mayoría de los casos, sin embargo, de manera general las gráficas experimental y teórica son semejantes en su forma.
4. Conclusiones
Con base en los resultados de la experimentación y los resultados teóricos de los modelos, se puede argumentar que el método para la obtención de frecuencias con el uso de la transformada de Fourier, es adecuado debido a que los resultados son semejantes entre frecuencias experimentales y teóricas.
El factor de amortiguamiento obtenido mediante el ancho de banda es coherente en cuanto a los valores obtenidos por piso, debido a que cada piso proporcionó valores similares de factores de amortiguamientos por modo y dichos factores fueron útiles para la modelación teórica, y así poder obtener la matriz de amortiguamiento y las respuestas dinámicas.
La modelación experimental del modelo, nos ayudó a observar de manera real cómo se comporta un modelo ante la aplicación de una aceleración sinusoidal o aceleración de un sismo escalado, y permitió verificar los valores obtenidos analíticamente respecto de los experimentales.
Como trabajo futuro se puede implementar la obtención de propiedades dinámicas de sistemas tridimensionales que presenten irregularidad en planta y elevación.
Se puede observar un desfase entre las respuestas experimentales y las teóricas en cuanto a las aceleraciones absolutas, a causa de la consideración del tiempo 0, en que los modelos experimentales estaban en estado de reposo.