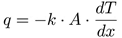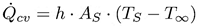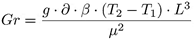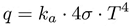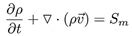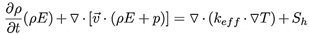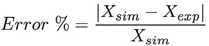Forma sugerida de citación: Quitiaquez, W.; Estupiñán-Campos, J.; Isaza-Roldán, C. A.; Toapanta-Ramos, F. y Lobato-Campoverde, A. (2020). «Análisis numérico de un sistema de calentamiento de agua utilizando un colector solar de placa plana ». Ingenius. N.◦ 24, (julio-diciembre). pp. 97-106. doi: https://doi.org/10.17163/ings.n24.2020.10.

1. Introducción

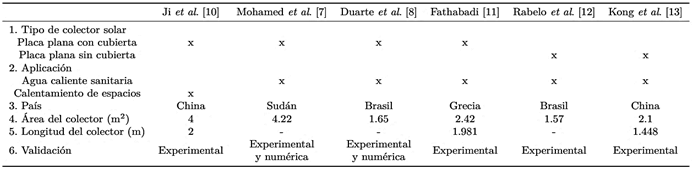
En la actualidad se ha visto como la comunidad científica ha tomado conciencia acerca del uso de fuentes renovables de energía gracias a los numerosos estudios de los perjuicios producidos por la quema de combustibles fósiles para la generación y uso de energía. Razón por la cual, en los últimos años se han incrementado las investigaciones y trabajos experimentales sobre el uso de la energía solar para el aumento de temperatura de los fluidos por medio de colectores solares térmicos; entre estos se tiene a los colectores solares concentrados que han determinado que el rango operativo varíe entre 50 y 300 °C ^[1]. El aprovechamiento de este recurso virtualmente renovable incide con mayor fuerza en lugares con una ubicación geográfica propicia para optimizar el desempeño de los dispositivos de transferencia de calor con ayuda de energía solar, debido al ángulo de incidencia propicio e invariante por influencia de las estaciones como es el caso de países en la región ecuatorial como Ecuador ^[2]. Ayompe y Duffy ^[3], en su investigación sobre el rendimiento térmico de un sistema solar de calentamiento de agua con colectores de placa plana aplicado en un sistema de escala doméstica de circulación forzada por un año, muestran que los resultados obtenidos fueron de energía diaria recolectada con un promedio anual de 19.6 MJ / día, una fracción solar de 32.2 %, adicionalmente, una eficiencia del colector y del sistema de 37.8 y 45.6 % respectivamente. En el funcionamiento de un colector solar se involucran varios agentes externos como la temperatura ambiente, la irradiación, posición geográfica, entre otros, como afirman Hashim et al. ^[4]. En su trabajo muestran la influencia que presenta el flujo volumétrico en la temperatura que puede alcanzar el fluido de trabajo al salir del colector solar; en su investigación experimental, realizaron dos pruebas con un caudal de 5.3 y 6.51 L·min−1 respectivamente, obteniendo como resultado temperaturas de salida de 51.4 y 49 °C, llegando a la conclusión que a menor flujo volumétrico mayor temperatura a la salida del colector podrá ser alcanzada. La dinámica computacional de fluidos (CFD, por sus siglas en inglés) es de gran ayuda en estudios que buscan mejorar el rendimiento en dispositivos de transferencia de calor. Es por esta razón por la que es utilizada con regularidad para desarrollar diseños mejorados de varios mecanismos que requieren transferencia de energía como calentadores de aire solares y para evaluar el potencial de generación de energía ^[5]. Marroquín et al. ^[6], en su investigación utilizan el software de simulación ANSYS, en específico su biblioteca correspondiente para dinámica de fluidos (CFD). Para el mallado se utiliza CFX-Mesh donde se considera un espacio de cara en los elementos entre 0.004 y 0.08 m, un ángulo de resolución de 30°; con respecto a la simulación, esta se desarrolla bajo el modelo de energía k-epsilon debido al flujo turbulento, obtenido un resultado que varía en un 5 % con la experimentación. Es posible realizar un análisis comparativo con la validación del análisis CFD con resultados experimentales en busca de encontrar un margen de error permisible como afirman Mohamed et al. ^[7], quienes en su estudio de una bomba de calor multifuncional de expansión directa (DX-SAMHP, por sus siglas en inglés) toman parámetros reales como temperatura exterior ambiente en invierno de -1 a 5 °C, radiación solar de 0, 57, 100 y 200 W·m−2 para ingresarlos al simulador, obteniendo valores en el modelado mayores que los resultados experimentales con desviaciones promedio de ± 4 %. En la investigación de Duarte et al. ^[8], se presenta en manera semejante un estudio comparativo validando los resultados del modelo matemático con valores experimentales, donde se utiliza una bomba de calor con un colector/evaporador de 1.65 m2 , temperatura ambiente entre 27.1 y 31.6 °C, radiación solar entre 0 y 811 W·m−2 , entre otros parámetros, gracias a lo cual, la simulación genera una diferencia en el COP de 1.6 %, menor a la incertidumbre experimental de 5 %. La eficiencia de los colectores solares de placa plana, de forma similar pueden variar por influencia de otras condiciones como las secciones transversales en las cuales se mueve el fluido de trabajo como muestran Andrade et al. ^[9], quienes validan su investigación mediante simulación CFD; adicionalmente, muestran una temperatura final en la salida de la tubería de 330 K y una eficiencia de 68 %. Existen numerosas investigaciones ^[7], ^[8], ^[10], ^[11], ^[12], ^[13] sobre el uso de colectores solares dentro de sistemas de calentamiento, las cuales son llevadas a cabo en diversos países como se muestra en la Tabla 1, donde validan de forma experimental propuestas en simulación para un desarrollo más exacto. De igual manera, algunos trabajos buscan validar de forma numérica propuestas experimentales para encontrar limitantes en el diseño, esto muestra la importancia de la complementariedad entre la parte de simulación y la experimental.

Tabla 1. Investigaciones realizadas en diferentes sistemas con colectores solares de placa plana 

1.1. Descripción del colector solar

El diseño del equipo utilizado para el desarrollo del presente estudio consiste en un tubo donde ocurre el intercambio de energía al fluido de trabajo (agua) cubierto por una plancha metálica con dos aletas como se ilustra en la Figura 1.

Figura 1. Diagrama esquemático del colector solar 

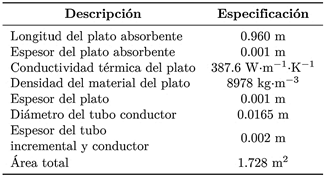
En busca de mejorar la transferencia de calor en el dispositivo y así incrementar de forma considerable su eficiencia, el material tomado en cuenta en el modelo del colector solar es cobre para la cubierta metálica con las alteas y el tubo por el que atraviesa el fluido de trabajo con dimensiones que se especifican en la Tabla 2, tomando en cuenta las variables que inciden directamente en el aumento de temperatura en el fluido, entre la entrada y la salida del colector.

Tabla 2. Especificaciones detalladas del colector solar 

1.2. Principio de funcionamiento del sistema

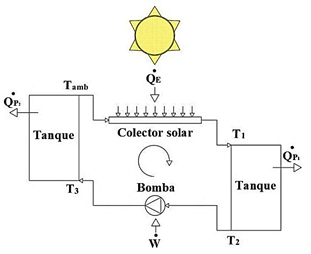
El fluido de trabajo inicia su recorrido en el sistema al ingresar a temperatura ambiente (Tamb) en el colector solar donde gracias al calor transferido por la energía solar (QE) alcanza una temperatura de salida (T1) mayor a la de entrada, posteriormente ingresa a un tanque donde pierde parte del calor ganado (QP1) hasta ingresar a la bomba donde gana un trabajo (W) para trasladarse a un segundo tanque donde pierde el resto del calor ganado en el colector solar (QP2) y reingresar al colector solar a temperatura ambiente como se detalla en la Figura 2.

Figura 2. Ciclo del fluido de trabajo en el colector solar 

2. Materiales y métodos

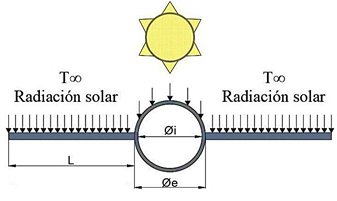
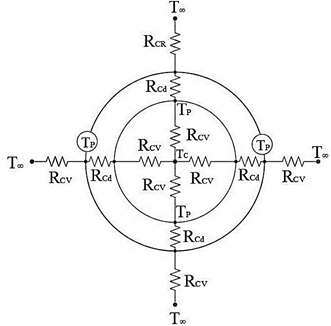
En un colector solar el calor es transferido de tres formas diferentes: conducción, convección y radiación, las cuales ocurren debido a la radiación solar incidente en el dispositivo, la diferencia de temperatura que existe entre el fluido de trabajo y el aire en el ambiente (T∞), tal como se aprecia en la Figura 3.

Figura 3. Transferencia de calor en un colector solar 

La convección y radiación ocurre debido a la transferencia de calor a través del aire en el ambiente hasta la superficie del dispositivo y a la energía solar que recibe el colector, respectivamente. Mientras que la conducción sucede por la transferencia de calor entre la superficie del colector solar como se muestra en la Figura 4.

Figura 4. Red de resistencias térmicas en un colector solar 

La transferencia de calor por conducción (q), explicada por la ley de Fourier, es proporcional al gradiente de temperatura (dT /dx) multiplicado por área (A), a través de la cual se transfiere la energía; la relación de la temperatura local (T), la distancia en la dirección del flujo de calor (x) y la conductividad térmica (k) se muestran en la Ecuación (1) ^[14].

(1)

El intercambio de calor por convección (Qcv) para un modelo se puede expresar como el proceso de convección de calor entre las superficies internas y externas de la envoltura de una superficie como se expresa en la Ecuación (2) ^[15].

(2)

Donde (h) representa el coeficiente de transferencia de calor por convección, (AS) al área superficial, (TS) la temperatura de la superficie y (T∞) la temperatura del fluido a cierta distancia de la superficie. Se debe considerar que la temperatura del fluido es igual a la de la superficie del sólido en la zona de contacto ^[16]. Al hablar de convección es importante clasificarla en dos tipos: natural o libre y forzada. La intensidad de la convección natural se mide por el número de Grashof (Gr) y Prandtl (P r), el cual se muestra en la Ecuación (3), estos números son característicos de la convección libre, pues al existir un incremento en estos números adimensionales, la transición el régimen de flujo se vuelve insignificante como afirman Meyer y Everts ^[17].

(3)

Donde (g) representa la gravedad, (∂) la densidad, (β) el coeficiente de expansión volumétrica, (T2 y T1) son las temperaturas de frontera, (L) la longitud de pared y (µ) la viscosidad dinámica ^[18]. La transferencia de calor por convención libre es cuantificable por medio del número de Nusselt, el cual varía en función de las condiciones en las que se produzca el intercambio de calor, en este caso siendo convección libre, se encuentra en dependencia del número adimensional de Rayleigh (Ra) mostrado en la Ecuación (4), que resulta de la multiplicación del número de Grashof con Prandtl ^[19].

(4)

Para lograr el cálculo correcto del número de Rayleigh es necesario tomar en cuenta al coeficiente de expansión volumétrica, la temperatura del fluido (T2), la temperatura de la pared del recinto (T1), el radio del recinto (R), la viscosidad cinemática (ν) y la difusividad térmica (α) ^[20]. La radiación térmica es aquella energía emitida por cualquier tipo de materia que se encuentre a una temperatura mayor a cero y cuya difusión de energía se muestra en la Ecuación (5) donde se presenta ^[21].

(5)

En la Ecuación (5) se presenta la transferencia de calor de la fuente radiactiva (q), la conductividad térmica (ka), la constante de Stefan-Boltzmann (σ = 5.67 × 10−8 W · m−2 · K−4) en unidades del Sistema Internacional (SI) y la distribución de temperatura debido al límite del medio físico (T) ^[22].

2.1. Parámetros de entrada del fluido a un colector solar plano

Ciertas condiciones importantes en la admisión del fluido de trabajo en un colector solar plano fueron: velocidad, flujo másico, presión manométrica, temperatura ambiente, entre otros, como se aprecia en la Tabla 3, con una recopilación de diferentes investigaciones donde se muestran las condiciones de entrada de un colector solar ^[23], ^[24], ^[25].

Tabla 3. Condiciones del fluido a la entrada del colector solar 

2.2. Mallado y modelado

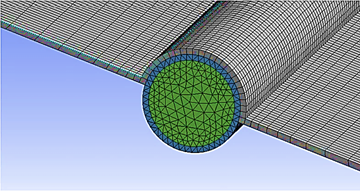
Para analizar de manera correcta las diferentes propiedades de los sólidos, líquidos y gases con el software de simulación es necesario construir una malla computacional eficiente, que puede estar constituida por células piramidales, tetraédricas o hexaédricas que dividen al cuerpo en varios subconjuntos más pequeños ^[26]. Para generar un correcto mallado de la sección del fluido es recomendable utilizar células tetraédricas por su adaptabilidad con las regiones curvas por donde atraviesa el fluido. La independencia del mallado es importante para determinar el número óptimo de malla, esto significa que la solución es independiente de la resolución de mallado. En el análisis 3D CFD es común llevar a cabo simulaciones utilizando diferentes tamaños de malla para comparar los resultados, a pesar de esto es posible encontrar variaciones menores al 0.5 % en temperaturas, mostrando la carencia de un impacto significativo en los resultados ^[27]. En el presente caso de estudio fue requerido un mallado diferenciado como se ilustra en la Figura 5. Para obtener el mallado se utilizó un método de patch conforming tipo tetrahédrico en las figuras curvas del fluido de trabajo y el tubo que lo contiene, edge sizing a lo largo de las uniones entre las aletas y el arco en la pared del colector con un ángulo de curvatura 5°, el cual se muestra en la Tabla 4 como malla 1, de esta forma, se utilizan hexaedros y tetraedros típicos en el análisis CFD de los colectores solares, distribución heterogénea de sus elementos y diferente número de elementos vecinos, lo que representan un mallado no estructurado para mejorar la convergencia del resultado ^[28]. Debido a la búsqueda de resultados con alta fiabilidad fue necesario establecer un mallado eficiente y, por consecuencia, con un número adecuado de nodos y elementos. Sin embargo, se realizó un análisis comparativo entre diferentes variedades de mallados con distintas calidades y número de elementos, como se muestra en la Tabla 4, para comprobar la eficiencia del mallado en la presente investigación; como resultado se tomó el modelo de malla 1 con rangos de excelente calidad señalados previamente.

Figura 5. Malla del colector solar 

Tabla 4. Condiciones del fluido a la entrada del colector solar 

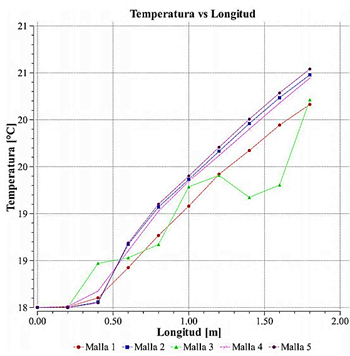
Con la ayuda de la calidad de la malla se puede apreciar en la Figura 6, el diferente tipo de tendencias que genera la simulación CFD con su variabilidad de resultados, lo cual, deriva en la selección final de un mallado en particular.

Figura 6. Variación de resultados con diferente mallado 

El software de simulación CFD para realizar el modelado de los fluidos dinámicos emplea las ecuaciones de Navier-Stokes, las cuales toman en cuenta la conservación de la continuidad, el momento y la energía como se muestra en las Ecuaciones (6), (7) y (8), respectivamente ^[29].

(6)

(7)

(8)

Al realizar la validación de los resultados de la simulación CFD es importante conocer el rango permisible de la variación que estos pueden tener con respecto a los valores experimentales del mismo estudio; este rango se puede medir con el error porcentual presentado en la Ecuación (9) y según distintos autores, el valor permisible se encuentra como máximo en 5.2 % ^[30].

(9)

3. Resultados y discusión

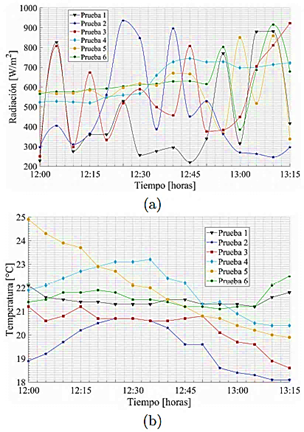
El módulo de radiación del software de simulación CFD, calculadora solar, permitió el análisis del colector solar de placa plana con parámetros de latitud (-0.225219), longitud (-78.5248) y diferentes horarios para determinar parámetros como temperatura superficial del dispositivo de transferencia de calor como se muestra en la Figura 7 (a y b) con horarios de 11:00 a 12:00, respectivamente, donde es posible apreciar una mayor distribución de temperatura debido al pico de radiación existente a las 12:00 con un valor máximo de 27.12 °C; la misma que se atenúa a medida que transcurre el tiempo como se aprecia a las 13:00 con un menor valor de temperatura en la superficie de la aleta de 24.63 °C. La radiación incidente en el colector se encuentra directamente relacionada con el horario en el cual se realiza la prueba, como se aprecia en la Figura 8 (a y b), generando valores pico entre las 12:00 y las 13:15 con valores de radiación disponibles entre 650 y 800 W·m−2 , respectivamente, influyendo de igual manera en la temperatura ambiente, un parámetro de suma importancia en la transferencia de calor hacia el dispositivo y su rendimiento.

Figura 7. Temperatura en la pared exterior del colector solar 

Figura 8. Variación de a) Radiación, b) Temperatura. 

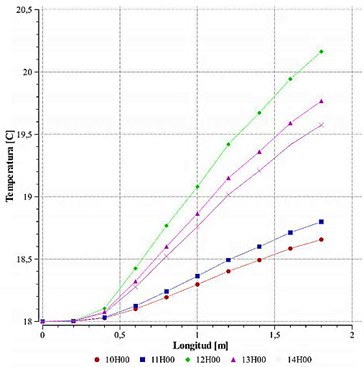
Debido a las variaciones comunes de los niveles de radiación que fluctúan entre 350 y 800 W·m−2 en la zona con latitud y longitud establecidos previamente, junto con el cambio de temperatura y flujo de calor en la superficie del dispositivo de transferencia de calor, es posible apreciar una mayor temperatura en el centro del fluido de trabajo a lo largo del centro del tubo en el colector solar en ciertos horarios específicos como se ilustra en la Figura 9, debido a esto, se determina que la mayor temperatura a la salida del colector ocurrirá a las 12:00 con un valor de 20.2 °C y con el menor valor de 18.65 °C a las 10:00 al recorrer la totalidad de la longitud del intercambiador de calor de placa plana.

Figura 9. Diagrama comparativo de temperatura vs. longitud en el centro del colector 

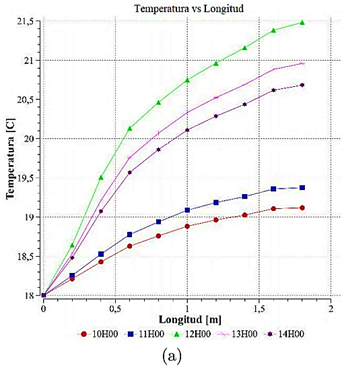
Es posible apreciar un mayor aumento de temperatura a medida que el fluido se acerca a la pared del tubo en el intercambiador de calor como se aprecia en la Figura 10 (a), donde la temperatura es medida a lo largo del colector solar en un espacio intermedio entre la pared del tubo y centro, adicionalmente se ilustra en la parte (b) de esta figura a la variación de temperatura en la pared del colector.

Figura 10. Diagramas comparativos de temperatura vs. longitud a) a ¼ de la superficie, b) superficie 

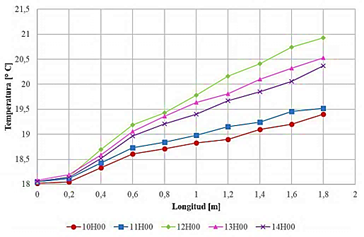
Los resultados de la simulación CFD presentes en la Figura 9 muestran la misma tendencia que los resultados experimentales como se aprecia en la Figura 11 validando los resultados dentro de un margen de error del 4.01 % dentro del análisis en el centro del colector solar en los diferentes horarios.

Figura 11. Diagrama comparativo de temperatura vs. longitud con resultados experimentales 

Al realizar el análisis comparativo entre los resultados experimentales con los determinados en la simulación numérica es posible encontrar una tendencia similar en ambos casos como se muestra en la Figura 12. De la misma manera, es posible apreciar un error porcentual máximo de 4.01 %, validando los datos experimentales y de la simulación.

Figura 12. Diagrama comparativo en el análisis experimental y numérico a las 12:00 

4. Conclusiones

En el presente estudio el análisis del rendimiento de un colector solar de placa plana fue realizado mediante un software de simulación CFD en el cual se ha utilizado en las diversas simulaciones realizadas, la radiación solar en diferentes horarios, la cual influye directamente en la transferencia de energía térmica hacia el fluido de trabajo mostrando varios resultados. El valor máximo de temperatura en el fluido a la salida del colector solar es de 20.16 °C presente a las 12:00, mientras que a las 10:00 se muestra la temperatura más baja de salida del fluido con 18.65 °C debido a la baja radiación solar propia de ese horario; valores que representan una tendencia favorable para la utilización del fluido en diferentes procesos, todo esto sin descartar el uso de procesos independientes de calentamiento de fluidos para alcanzar una temperatura específica en busca de cubrir una determinada necesidad. Debido al pico de radiación presente a las 12:00, se genera un valor máximo de flujo de calor hacia el fluido de trabajo de 96.02 W·m−2 mostrando la mayor cantidad de transferencia de energía en todo el rango de análisis tomado en cuenta en la investigación. Es posible apreciar una variación en la temperatura de la superficie exterior del dispositivo de transferencia de calor acorde con los niveles de radiación típicos de los diferentes horarios estudiados mostrando un valor máximo de 27.12 °C y un valor mínimo de 20.48 °C a las 12:00 y 10:00 respectivamente. Finalmente, se puede corroborar que los resultados de la simulación al ser comparados con los datos experimentares difieren en un 4.01 %.

Agradecimientos

Los autores agradecen a la Universidad Politécnica Salesiana, Universidad Pontifica Bolivariana y la alianza «Energética 2030» (Programa de Investigación con código No. 58667), de la convocatoria «778-2017 Ecosistema Científico» de COLCIENCIAS, financiado por el Banco Mundial. El programa de investigación es administrado por el Ministerio de Ciencia, Tecnología e Innovación (Minciencias) a través del contrato No. FP44842-210-2018.