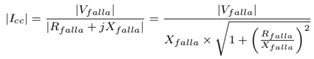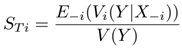Forma sugerida de citación: Moronta R. José A. y Rocco Claudio M. (2020). «Estimación del efecto de la resistencia en la corriente de cortocircuito mediante un análisis de sensibilidad». Ingenius. N.◦ 24, (julio-diciembre). pp. 9-16. doi: https://doi.org/10.17163/ings.n24.2020.01.

1. Introducción

Los estudios de cortocircuito son análisis mediante los cuales se determinan las magnitudes de las corrientes eléctricas que circulan en los sistemas eléctricos de potencia (SEP), durante una falla. Posteriormente, dichas magnitudes son utilizadas para especificar o validar las características de los componentes del sistema, tales como interruptores, barras, entre otros ^[1].

Los estudios de cortocircuito en los SEP, suponen generalmente que la resistencia eléctrica de los elementos del sistema es despreciable, y solo consideran exclusivamente la reactancia eléctrica de estos para el cálculo de la magnitud de la corriente de cortocircuito. De acuerdo con ^[2], para la mayoría de los cálculos de corriente de cortocircuito en media o alta tensión, y en algunos casos en baja tensión, cuando las reactancias son «mucho más grandes» que las resistencias, es lo suficientemente preciso, y más simple, despreciar las resistencias y usar solo las reactancias. Nótese como la norma no es específica, solo sugiere cuando la reactancia sea mucho mayor que la resistencia.

La misma consideración para el cálculo de corrientes de cortocircuito se realiza en el estándar ^[3], donde indican que el cálculo se hace mucho más fácil, pero con pérdida en la precisión, si se desprecian las resistencias, esto cuando la relación reactancia/resistencia (X/R) sea mayor a 3,33.

La bibliografía relacionada con los análisis de SEP sugiere procedimientos similares, en cuanto a la posibilidad de despreciar la resistencia de los elementos. Por ejemplo, en ^[1] indican que es posible despreciar las resistencias en los estudios de fallas, porque «no es probable que influyan significativamente en el nivel de la corriente de falla».

En ^[4] se presenta un conjunto de suposiciones para el cálculo de cortocircuito, donde sugieren despreciar todas las resistencias de los elementos (generadores, transformadores y líneas de transmisión) para simplificar el cálculo. Otros trabajos ^[5, ^6], establecen como un error máximo de 5 % para el valor de la corriente de cortocircuito si se desprecia la resistencia de los elementos del sistema. Esta sugerencia se deriva a partir de la expresión general para determinar de la corriente de falla, ver Ecuación (1).

(1)

Donde:

Donde la Rfalla y Xfalla corresponden a la impedancia de Thevenin equivalente en el punto de falla. Cuando la relación X/R es mayor a 4, el error que se comete al despreciar la resistencia es menor al 4 %. Esto es válido excepto para sistemas de distribución o industriales donde esta relación es menor que 4 ^[6]. En los sistemas de potencia, el valor de la resistencia de los elementos suele ser muy pequeño comparativamente con el de su reactancia. Esta consideración es la razón en la cual se basan las normas y los autores para despreciar las resistencias y su influencia en la determinación de las corrientes de falla. En sistemas de potencia reales, la relación X/R entre la reactancia y la resistencia en el punto de falla suele ser del orden de entre 15 y 120 veces ^[7]. Las referencias concuerdan en que puede despreciarse la resistencia eléctrica en los análisis de cortocircuito, pero no hay un consenso en cuanto a su efecto en las magnitudes de las corrientes de cortocircuito. En este trabajo, para dos redes de la literatura, se cuantifica el efecto de variar la resistencia, en el valor de la corriente de cortocircuito, mediante el análisis de sensibilidad (AS). Adicionalmente se define la relación de estas variaciones con el resto de parámetros que permiten determinar la corriente de cortocircuito (tensión y reactancia eléctrica de los elementos). El análisis se basa en el uso de la teoría de AS y AI, como resultado de estos análisis se llega en forma directa a la misma conclusión presentada en la literatura, pero desde una perspectiva diferente. La estructura del trabajo es como sigue: la primera sección presenta algunas definiciones fundamentales asociadas al análisis de sensibilidad; la segunda describe el procedimiento para la determinación de la incertidumbre asociada a la corriente de cortocircuito y los sistemas eléctricos de potencia de prueba; la tercera

Donde la R_falla y X_falla corresponden a la impedancia de Thevenin equivalente en el punto de falla. Cuando la relación X/R es mayor a 4, el error que se comete al despreciar la resistencia es menor al 4 %. Esto es válido excepto para sistemas de distribución o industriales donde esta relación es menor que 4 ^[6]. En los sistemas de potencia, el valor de la resistencia de los elementos suele ser muy pequeño comparativamente con el de su reactancia. Esta consideración es la razón en la cual se basan las normas y los autores para despreciar las resistencias y su influencia en la determinación de las corrientes de falla. En sistemas de potencia reales, la relación X/R entre la reactancia y la resistencia en el punto de falla suele ser del orden de entre 15 y 120 veces ^[7].

Las referencias concuerdan en que puede despreciarse la resistencia eléctrica en los análisis de cortocircuito, pero no hay un consenso en cuanto a su efecto en las magnitudes de las corrientes de cortocircuito. En este trabajo, para dos redes de la literatura, se cuantifica el efecto de variar la resistencia, en el valor de la corriente de cortocircuito, mediante el análisis de sensibilidad (AS). Adicionalmente se define la relación de estas variaciones con el resto de parámetros que permiten determinar la corriente de cortocircuito (tensión y reactancia eléctrica de los elementos). El análisis se basa en el uso de la teoría de AS y AI, como resultado de estos análisis se llega en forma directa a la misma conclusión presentada en la literatura, pero desde una perspectiva diferente. La estructura del trabajo es como sigue: la primera sección presenta algunas definiciones fundamentales asociadas al análisis de sensibilidad; la segunda describe el procedimiento para la determinación de la incertidumbre asociada a la corriente de cortocircuito y los sistemas eléctricos de potencia de prueba; la tercera presenta y comenta los resultados obtenidos y finalmente, la cuarta presenta las conclusiones y trabajos futuros.

1.1. Análisis de sensibilidad e incertidumbre

El análisis de incertidumbre (AI), de acuerdo con ^[8], se define como el estudio de cuánta incertidumbre en la salida de un modelo aportan las diferentes fuentes de incertidumbre de la entrada. Por otra parte, el análisis de sensibilidad (AS) evalúa la importancia de las variables de entrada de un modelo. Dicha importancia se mide en función de cuánta variabilidad de la salida del modelo es debida a la variabilidad de las variables de entrada. En este caso, la incertidumbre de las variables de entrada es modelada a través de funciones de distribución, de parámetros conocidos. De acuerdo con ^[8], se definen los pasos para realizar el enfoque de AS/AI:

• Establecer el objetivo de análisis y en consecuencia definir la forma de la o las salidas del modelo.

  Decidir cuáles factores de entrada se quiere incluir en el análisis.

  Elegir una función de distribución de probabilidad para cada uno de los factores de entrada.

  Elegir un método de AS, de acuerdo con las características del problema a estudiar.

  Generar la muestra de los factores de entrada. La muestra es generada según las especificaciones de los parámetros conocidos y el tamaño de muestra seleccionado.

  Evaluar la muestra generada en el modelo y producir la o las salidas del mismo, que contiene los valores según la forma especificada en el paso 1.

  Analizar las salidas del modelo, determinar los índices de sensibilidad (importancia) y establecer las conclusiones.

Los métodos de AS, pueden clasificarse según la salida de sus medidas: cuantitativos o cualitativos, locales (no permiten variar todos los factores simultáneamente) o globales (permiten variar todos los factores simultáneamente) y dependientes o independientes del modelo ^[9]. Dado un modelo Y = F(X1, X2, X3, . . . , Xn) donde Y es la salida del mismo y Xi representan las variables de entrada modeladas como variables aleatorias (es decir, su incertidumbre es modelada como una función de densidad de probabilidades (fdp)), la varianza V (Y ) de la salida Y puede ser descrita como en la Ecuación (2) ^[8]:

(2)

Donde:

• V_i = V (E(Y lX_i)) es el efecto principal (o de primer orden) debido a x_i

  V_ij = V (E(Y lX_i , X_j )) − V_i − V_j es el efecto de segundo orden producto de la interacción entre x_i y x_j, y así sucesivamente.

Los efectos de sensibilidad principal (Si), y total (STi) pueden definirse como sigue en las Ecuaciones (3) y (4), respectivamente, según ^[8]:

(3)

(4)

Donde:

• X_−i = (x₁, x₂, . . . x_i−1, x_i+1, ..., x_k) y E−i(Y | X_i) es el valor esperado de Y condicionado a x_i, y, por tanto, es una función de x_i solamente.

El índice principal S_i es la fracción de la varianza de la salida V(Y) que puede atribuirse únicamente a x_i, mientras que STi corresponde a la fracción de V(Y) que puede atribuirse a x_i, incluyendo todas sus interacciones con las demás variables de entrada. El índice principal de S_i es la medida empleada para determinar las variables de entrada que mayoritariamente afectan la incertidumbre de salida, mientras que S_Ti se utiliza para identificar el subconjunto de variables de entrada no influyentes, es decir, aquellas variables que pueden ser fijadas en cualquier valor dentro de su rango de incertidumbre, y no afectan significativamente la varianza de salida ^[10].

Las estimaciones de S_i y S_Ti se aproximan: 1) suponiendo independencia (estadística) entre las variables de entrada; 2) usando técnicas de muestreo particulares para generar muestras de las variables de entrada; y 3) evaluando el conjunto de las muestras obtenidas en 2) a partir del modelo en estudio [8]. Existen diversas técnicas para análisis de sensibilidad basadas en la descomposición de la varianza, se mencionan diversas de estas en [10]. Estas técnicas difieren en cuanto a la complejidad computacional, así como en los efectos que evalúan (principales y/o totales). Entre estas técnicas, cabe destacar: Sobol ^[11] que permite evaluar los efectos principales y totales, y EFAST (Extended Fourier Amplitude Sensitivity Test) ^[12], una extensión de FAST (Fourier Amplitude Sensitivity Test) ^[13] que también evalúa los efectos principales y totaltes (S_i y S_Ti) pero con menor complejidad computacional que el método de Sobol.

2. Metodología

Para estimar el efecto de la resistencia eléctrica de los elementos (variables de entrada del modelo) sobre la corriente de cortocircuito (salida del modelo), se propone el siguiente enfoque:

Se supone para las variables de entrada (tensión prefalla, resistencia y reactancia de los elementos del sistema de potencia) una distribución uniforme: U[0 − 1, 2 × valor base]. La distribución es asimétrica y permite cuantificar el efecto de despreciar (valores cercanos a cero) la resistencia de los elementos del sistema de potencia. Posterior a la evaluación del procedimiento descrito (AS), se realiza una simulación de Monte Carlo ^[14] considerando únicamente las variables de interés (resistencia eléctrica de los elementos).

La simulación de Monte Carlo es un método que se emplea para evaluar la propagación de incertidumbre a través de la generación de variables aleatorias. De esta manera, se cuantifica la propagación de la incertidumbre a la salida del modelo, es decir, cuantifica la variación de la magnitud de la corriente de cortocircuito. El cálculo de cortocircuito y el AS/AI se realizaron en el software libre R ^[15], para el AS se utilizaron específicamente los algoritmos de la librería Sensitivity.

2.1. Sistemas eléctricos de prueba

2.1.1. Sistema de potencia de prueba 1 (SEP1)

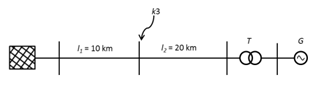
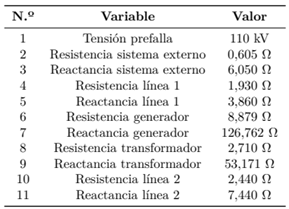
El sistema de potencia empleado ^[16] es una red eléctrica no mallada con dos fuentes, como muestra la Figura 1. Está compuesto por un sistema externo, dos líneas de transmisión, un transformador y un generador. Se asume una falla trifásica sólida a tierra en k3.

Figura 1. Sistema de potencia de prueba radial (SEP1) 

Se modelan los elementos del sistema de potencia de prueba radial (SEP1), los valores se muestran en la Tabla 1. Estos valores representan las variables de entrada del modelo de AS.

Tabla 1. Impedancia de los elementos del sistema de potencia de prueba 1 (SEP1) 

2.1.2. Sistema de potencia de prueba 2 (SEP2)

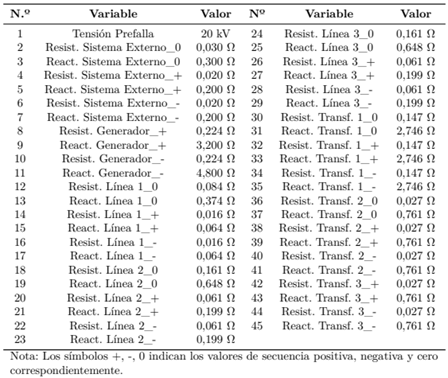
La red eléctrica mallada tomada de [16], para la cual se supone una falla monofásica sólida a tierra en k1 (ver Figura 2). Los valores de los elementos se muestran en la Tabla 2, estos son los factores de entrada para el análisis de sensibilidad.

Figura 2. Sistema de potencia de prueba mallado (SEP2) 

Por ser una falla monofásica se resuelve mediante el método de las redes de secuencia ^[1], y los elementos deben modelarse con sus valores correspondientes de secuencia positiva, negativa y cero. Es decir, los parámetros que intervienen en el AS se incrementan por 3. Para una línea, por ejemplo, se tendrá una resistencia de secuencia positiva, negativa y cero.

Tabla 2. Impedancia de los elementos del sistema de potencia de prueba 2 (SEP2) 

3. Resultados

3.1. Sistema de potencia de prueba 1 (SEP1)

En la Figura 3 se muestran los índices de sensibilidad de primer orden (S_i) (sección blanca de las barras) y total (S_Ti) (la sección completa, blanca y gris) para el SEP1. Las variables que más afectan la corriente de cortocircuito, en orden de importancia, son: la tensión prefalla (S₁=0,456), la reactancia del sistema externo (S₃=0,252) y la reactancia de la línea 1 (S₅=0,108). El resto de los factores, incluyendo las resistencias de los elementos, tiene valores de importancia S_Ti muy pequeños, por lo que sus efectos se pueden considerar despreciables.

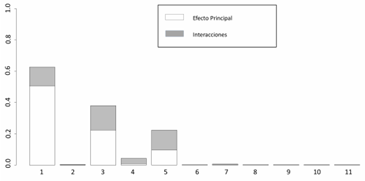
Figura 3. Efectos principales (S_i) y totales (S_Ti) de las variables de entrada en la corriente de cortocircuito del SEP1 

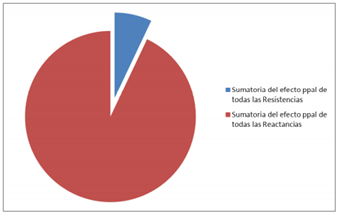
Como se mencionó, la tensión prefalla tiene una importancia muy alta (0,456), por esto, posteriormente se la fija como constante en el modelo, para evaluar únicamente los efectos de las reactancias y resistencias de los elementos, de igual manera se obtuvieron efectos muy pequeños para las resistencias. A manera de comparación, se agruparon todos los efectos principales de las resistencias y los efectos principales de las reactancias menos importantes, ver Figura 4, manteniendo constante la tensión prefalla. La sumatoria del efecto principal de las resistencias es despreciable frente a la suma del efecto principal de las reactancias, en este sistema y, para esta falla particular, la variable más importante es la reactancia del sistema externo.

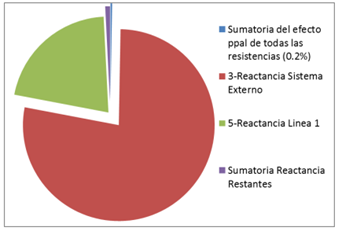
Figura 4. Efectos principales de las reactancias y la sumatoria de los efectos principales de las resistencias 

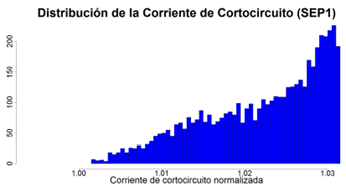
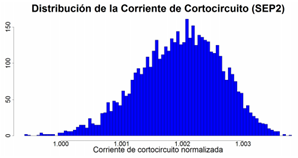
Posterior a la evaluación del AS, y considerando solo las resistencias de los elementos, se realiza la evaluación del método Monte Carlo ^[14], donde se obtiene la distribución de probabilidad aproximada de la corriente de cortocircuito para 5000 evaluaciones. La corriente de cortocircuito para los valores de la Tabla 1 es de 7196 A, lo cual corresponde con el valor normalizado de 1 unidad, en el histograma aproximado de la corriente de cortocircuito presentado en la Figura 5. Los valores mínimos y máximos obtenidos, para la corriente de cortocircuito, fueron de 0,995 y 1,031 veces. El valor promedio de esa distribución es de 1,022, la forma de la distribución es asimétrica, con una tendencia al extremo superior.

Figura 5. Histograma aproximado de la corriente de cortocircuito (SEP1) 

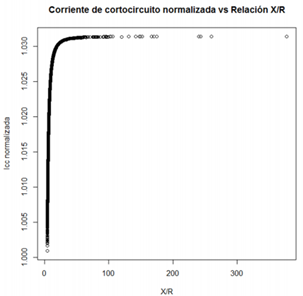
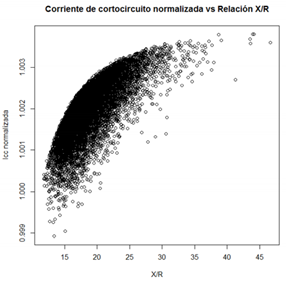
En la literatura se refiere a la relación X/R para despreciar la resistencia eléctrica en los cálculos de cortocircuito, por esto en la Figura 6 se muestra la corriente de cortocircuito normalizada para los valores X/R obtenidos en la simulación de Monte Carlo.

Figura 6. Corriente de cortocircuito normalizada para los valores X/R (SEP1) 

Los valores de la relación X/R varían desde aproximadamente 4 hasta 400, considerando en este amplio rango, la corriente de cortocircuito normalizada no presenta variaciones que alcancen un 4 % cuando menos.

3.2. Sistema de potencia de prueba 2 (SEP2)

Para el sistema de potencia mallado SEP2 se obtienen resultados similares al SEP1. La tensión prefalla resulta ser la variable más importante (ver Figura 7). En este sistema existe más incertidumbre de orden superior asociada a la interacción de las variables (S_Ti - S_i), esto es debido al hecho que el sistema es mallado, y para obtener la impedancia equivalente de cortocircuito deben calcularse varias impedancias equivalentes (sumas y productos sucesivos).

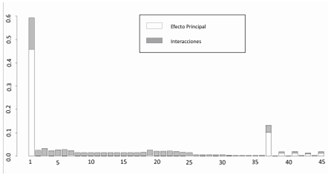
Figura 7. Efectos principales (Si) y totales (STi) de las variables de entrada en la corriente de cortocircuito del SEP2 

Los números de las variables (eje x) de la Figura 7, están en concordancia con la numeración de la Tabla 2. Nótese que la variable 37 (reactancia de secuencia del transformador 2 aparece como segunda variable importante, si bien con una contribución muy pequeña). En la Figura 8 se comparan la suma de los índices totales de las resistencias y de las reactancias del sistema SEP2, considerando constante la tensión prefalla, el porcentaje que representa el índice de la suma de las resistencias es de un poco menos del 7 %.

Figura 8. Sumatoria de los efectos principales de las resistencias y reactancias del SEP2 

La Figura 9 muestra el histograma aproximado para la corriente de cortocircuito, obtenido mediante la técnica de Monte Carlo perturbando solamente las resistencias de los elementos del sistema SEP2. Esta corriente para los valores de la Tabla 2 es de 13 679 A, lo cual corresponde con el valor normalizado de 1 unidad, en el histograma de la Figura 9. Los valores mínimos y máximos obtenidos, para la corriente de cortocircuito, fueron de 0,9999 y 1,0037. Nótese como realizando variaciones en las resistencias, el efecto sobre la corriente de cortocircuito es despreciable. Esta distribución es más simétrica que la del ejemplo anterior y tiene un valor promedio de 1,002.

Figura 9. Histograma aproximado de la corriente de cortocircuito (SEP2) 

La Figura 10 muestra la corriente de cortocircuito normalizada para los valores X/R obtenidos en la simulación de Monte Carlo para el sistema SEP2. En este caso la variación es mucho menor, la corriente de cortocircuito normalizada no presenta variaciones que alcancen un 1 %.

Figura 10. Corriente de cortocircuito normalizada para los valores X/R (SEP2) 

4. Conclusiones

En este trabajo se estima la incertidumbre de la corriente de cortocircuito debida a la resistencia eléctrica de los elementos, a partir de un enfoque de sensibilidad e incertidumbre. Este análisis puede aplicarse a cualquier otro sistema de potencia con cualquier ubicación y/o tipo de falla. Para los dos casos considerados, los resultados están en concordancia con lo que sugieren diversos autores: es posible despreciar la resistencia de los elementos, siempre que la reactancia sea mucho mayor que la resistencia de los mismos (relación X/R), la variación de la magnitud de la corriente de cortocircuito en los dos casos evaluados, no supera un 4 %, esto coincide con el valor de 4-5 % reportado en algunos trabajos consultados ^[5, ^6].

Este análisis no solo considera la incertidumbre de la corriente de cortocircuito, debido a las incertidumbres de las resistencias y reactancias, sino que permite cuantificar de la variación total, es decir, el porcentaje debido a la incertidumbre de las resistencias de los componentes del SEP. En estos dos casos, el efecto de la resistencia de los elementos es aproximadamente un 7 % (en sistema de potencia de prueba 2 (SEP2)), el resto está asociado a las reactancias, si se considera constante el valor de la tensión prefalla, para el análisis de sensibilidad realizado. Los resultados obtenidos en estos dos sistemas, pudieran ser extrapolables a sistemas de potencia reales en media o alta tensión, ya que en estos la reactancia suele ser mucho mayor que la resistencia (X≫R). Se pretende como trabajo futuro establecer relaciones y/o valores críticos entre el factor reactancia-resistencia (X/R) del punto de falla del sistema y los índices principales (Si) de la incertidumbre de la corriente de cortocircuito.