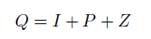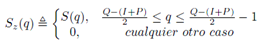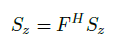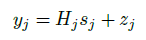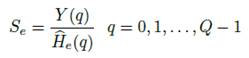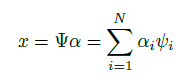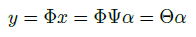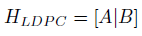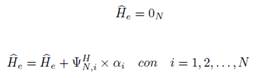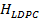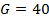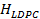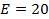Forma sugerida de citación:
Yanza-Verdugo, A.; Pucha-Cabrera, C. e Inga-Ortega, J. (2020). «Estimador de canal basado en sensado compresivo y LDPC para OFDM usando SDR». Ingenius. N.° 23, (enero-junio). pp. 74-85. doi: https://doi.org/10.17163/ings.n23.2020.07
1. Introducción
La técnica de transmisión más implementada en la actualidad en redes inalámbricas es multiplexación por división de frecuencias ortogonales (OFDM, del inglés Orthogonal Frequency Division Multiplexing) debido a sus ventajas en la transmisión de datos de alta velocidad a través de canales selectivos en frecuencia. Así, el uso de OFDM ha tenido alto rendimiento debido a su alta eficiencia en el uso del espectro radio eléctrico y su robustez al retardo por multitrayectos [1, 2]. Además, a través del uso de un prefijo cíclico se reduce la interferencia entre símbolos (ISI, del inglés Intersymbol Interference) y la interferencia entre portadoras (ICI, del inglés Inter Carrier Interference) permitiendo reemplazar el uso de complejos ecualizadores en el dominio del tiempo por un simple ecualizador en el dominio de la frecuencia [3]. En este sentido, para canales de radio selectivos en frecuencia y que varían en el tiempo en sistemas de comunicaciones móviles de banda ancha, es necesario aplicar estimación de canal confiable para implementar detección coherente [1].
Hay tres tipos de estimadores de canal: estimación ciega, estimación semiciega y modulación asistida por pilotos (PSAM, del inglés Pilot Symbol Assisted Modulation). PSAM usa símbolos piloto que son conocidos tanto por el receptor como por el transmisor en diferentes posiciones para obtener una aproximación del canal a cambio de perder eficiencia espectral. Por su parte, la estimación ciega está enfocada en procesos estadísticos con alto nivel matemático presentando mejoras con respecto a la eficiencia espectral, aunque no es muy utilizado en la actualidad debido a su alta complejidad, velocidad lenta para converger y bajo rendimiento [4]. La estimación semiciega usa una combinación de los dos anteriores para llegar a un convenio entre complejidad y eficiencia; para ello se utilizan tanto secuencias de entrenamiento como modelos estadísticos de canal [5].
De acuerdo con lo antes mencionado, este trabajo propone el uso de PSAM para la estimación de canal, donde la ganancia del canal y la distorsión de fase se obtienen a partir de la señal recibida en las posiciones de los símbolos piloto [1]. Estos símbolos piloto también son usados para mejorar la sincronización de tiempo y frecuencia en el sistema de comunicación. Sin embargo, para incrementar el rendimiento, es necesario del uso de un mayor porcentaje de símbolos piloto e implica que ciertas subportadoras no transmitan información [2].
Además, este trabajo con el objeto de mejorar la utilización del ancho de banda reduce el número de subportadoras piloto a través del uso de la teoría de sensado compresivo (CS, del inglés Compressive Sensing) en la estimación de canal. Esto se puede aplicar ya que es posible estimar el canal aprovechando la teoría de CS, al considerar que el número de símbolos piloto es disperso en relación con el número total de símbolos que conforman un mensaje OFDM obteniendo una versión comprimida del canal correspondiente a los efectos del mismo sobre las subportadoras piloto [6].
También, se optimiza el proceso en la implementación sobre equipos de radio definido por software (SDR, del inglés Software Defined Radio) a través del uso de la matriz de comprobación de paridad de baja densidad (LDPC, del inglés Low Density Parity Check) combinado con el paradigma de CS.
A partir de aquí, el artículo se ordena de la siguiente forma: en la sección 2 se discute el modelado matemático de OFDM, CS y la aplicación de matrices LDPC con CS. En la sección 3 se describe la implementación en los dispositivos SDR usando las matrices LDPC con CS. La sección 4 presenta los resultados obtenidos, el análisis del ancho de banda y el análisis de la tasa de error de bit (BER, del inglés Bit Error Rate). Finalmente, en la sección 5 se dan las conclusiones y recomendaciones para trabajos futuros.
2. Modelado matemático
La implementación se desarrolla a partir del modelo matemático de OFDM, donde un símbolo OFDM es representado por 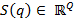 , así un conjunto
, así un conjunto 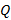 de símbolos de información es transmitido por el símbolo
de símbolos de información es transmitido por el símbolo 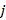 de OFDM, cada uno con una subportadora
de OFDM, cada uno con una subportadora 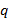 es
es 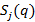 , por tanto
, por tanto 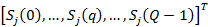 representa el vector de símbolos de información transmitidos en el
representa el vector de símbolos de información transmitidos en el 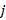 -ésimo símbolo OFDM [2-7]
-ésimo símbolo OFDM [2-7]
Cada símbolo OFDM usa el flujo serial de símbolos de información convirtiéndolos en Q flujos paralelos para luego insertar los símbolos piloto necesarios en la estimación del canal según el esquema de transmisión propuesto. Además, se adicionan subportadoras en cero para establecer bandas de guarda entre cada símbolo OFDM y así evitar la interferencia de canales adyacentes. La cantidad de subportadoras de un símbolo OFDM se evidencia en (1).
Donde I corresponde al número de subportadoras con información, P es el número de subportadoras piloto y Z es el número de subportadoras en cero para un símbolo OFDM. De acuerdo con esto, la Ecuación (2) describe el formato de un símbolo OFDM correspondiente al dominio de la frecuencia, luego se aplica la transformada inversa de Fourier (IDFT, del inglés, Inverse Discrete Fourier Transform) para obtener el símbolo en el dominio del tiempo tal como se describe en la Ecuación (3). La distribución del relleno de ceros se detalla en [8].
La reducción de ISI e ICI se da por el uso del llamado prefijo cíclico (CP) que consiste en una extensión cíclica del símbolo OFDM. El CP es tan largo como el retardo de propagación esperado y los efectos de ambos se encuentran en [9]. Por otra parte, la señal recibida para OFDM puede ser descrito como en la Ecuación (4).
El vector de símbolos de información recibidos es 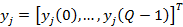 en el
en el 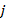 -ésimo símbolo OFDM,
-ésimo símbolo OFDM, 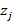 es el ruido gaussiano y
es el ruido gaussiano y 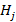 denota el valor del canal para el
denota el valor del canal para el 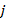 -ésimo símbolo OFDM, que es obtenido mediante el bloque de estimación de canal [7].
-ésimo símbolo OFDM, que es obtenido mediante el bloque de estimación de canal [7].
El receptor usa el algoritmo de Van de Beek que aprovecha el prefijo cíclico para establecer el inicio y el fin de un símbolo OFDM. Este algoritmo también permitirá corregir los efectos del canal en posibles desplazamientos de fase y evitar una pérdida de ortogonalidad en las subportadoras [10].
A continuación, se retira el prefijo cíclico y se aplica la transformada discreta de Fourier (DFT, del inglés, Discrete Fourier Transform) para recuperar los símbolos de información. Previo a la recuperación de los símbolos de información se estima el canal luego de remover el relleno de ceros y extraer los símbolos piloto. Los datos ecualizados se obtienen a través de la operación indicada en la Ecuación (5) [11]. En donde 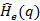 es el canal estimado. La Tabla 1 presenta una lista de todas las variables usadas a lo largo de este trabajo.
es el canal estimado. La Tabla 1 presenta una lista de todas las variables usadas a lo largo de este trabajo.
2.1. Sensado compresivo
Desde otra perspectiva, el paradigma de CS considera una señal «dispersa» 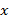 que posee solo
que posee solo 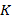 elementos diferentes de cero con
elementos diferentes de cero con 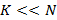 y donde
y donde 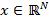 . Entonces, a través de una matriz
. Entonces, a través de una matriz 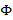 de
de 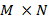 con
con 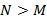 , llamada matriz de sensado, se busca concentrar la información más relevante de a través del uso de otro vector
, llamada matriz de sensado, se busca concentrar la información más relevante de a través del uso de otro vector 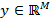 . Si esto no se cumple, se reduce la capacidad de reconstruir
. Si esto no se cumple, se reduce la capacidad de reconstruir 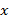 a partir
a partir 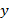 de ; a esta restricción se la conoce como condición de espacio nulo (NSP, del inglés Null Space Property) [11,12]. No es fácil encontrar señales consideradas «dispersas», no obstante, es posible encontrar una aproximación a este concepto que se da cuando la señal
de ; a esta restricción se la conoce como condición de espacio nulo (NSP, del inglés Null Space Property) [11,12]. No es fácil encontrar señales consideradas «dispersas», no obstante, es posible encontrar una aproximación a este concepto que se da cuando la señal 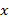 puede ser «comprimible» en alguna base vectorial diferente a la original [11
-
13]. Por tanto,
puede ser «comprimible» en alguna base vectorial diferente a la original [11
-
13]. Por tanto,  , donde
, donde 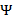 (también llamada matriz diccionario de
(también llamada matriz diccionario de 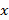 ) corresponde a la base vectorial en la que se proyecta
) corresponde a la base vectorial en la que se proyecta 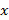 , y
, y 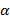 corresponde a los átomos de
corresponde a los átomos de 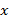 dentro del dominio de
dentro del dominio de 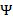 . Así se tiene que la señal original
. Así se tiene que la señal original  puede ser representada a través de la combinación lineal que propone en (6) [14]. El diccionario por ejemplo puede ser de Fourier, DCT o de Wavelet [11,15,16]
puede ser representada a través de la combinación lineal que propone en (6) [14]. El diccionario por ejemplo puede ser de Fourier, DCT o de Wavelet [11,15,16]
La compresión de la señal 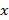 en la señal
en la señal  se puede obtener a través de (7) donde
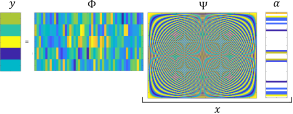
se puede obtener a través de (7) donde 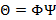 . La Figura 1(a) y la Figura 1(b) exponen de forma gráfica el concepto de CS [13,17].
. La Figura 1(a) y la Figura 1(b) exponen de forma gráfica el concepto de CS [13,17].
La literatura recomienda que  sea aleatoria para cumplir la propiedad de restricción isométrica (RIP, del inglés Isometric Restriction Property) y así x pueda ser reconstruida a partir de y [16, 18]. Las matrices de sensado en general se pueden obtener de un proceso aleatorio con distribución normal, consiguiendo un buen rendimiento durante la reconstrucción de la señal, pese a que, estas distribuciones pueden llegar a demandar muchos recursos [15, 16].
sea aleatoria para cumplir la propiedad de restricción isométrica (RIP, del inglés Isometric Restriction Property) y así x pueda ser reconstruida a partir de y [16, 18]. Las matrices de sensado en general se pueden obtener de un proceso aleatorio con distribución normal, consiguiendo un buen rendimiento durante la reconstrucción de la señal, pese a que, estas distribuciones pueden llegar a demandar muchos recursos [15, 16].
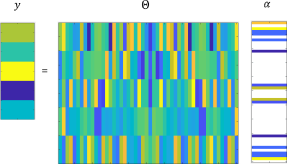
Figura 1. Principio de operación de sensado compresivo: (a) proceso de medición en CS con una matriz de sensado aleatorio Φ y matriz de medición Ψ. (b) proceso de medición con Θ = Φ Ψ.
Debido a que 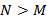 y que
y que 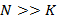 , el proceso de reconstrucción de
, el proceso de reconstrucción de 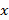 se convierte en un problema de optimización expuesto en la Ecuación (8) donde se busca obtener los átomos
se convierte en un problema de optimización expuesto en la Ecuación (8) donde se busca obtener los átomos  que minimicen el error de
que minimicen el error de 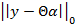 .
.
A partir de α se puede reconstruir x usando la Ecuación (6). Sin embargo, el problema de optimización no tiene solución ya que es del tipo NP Hard [11–13]. En este aspecto, los algoritmos de reconstrucción dispersa buscan relajar el problema de optimización para obtener una solución pseudoóptima. Además, pueden mejorar su rendimiento si se usa una matriz de sensado adecuada que permita la preservación de la información y garantice la reconstrucción de la señal original de manera única [15, 16, 19 – 2 2].
Entre los algoritmos de reconstrucción dispersa más populares usados en la aplicación de CS para la estimación de canal, destaca OrthogonalMatchingPursuit (OMP) perteneciente al tipo de algoritmos basados en búsqueda codiciosa. Así, OMP se basa en aproximaciones sucesivas de los coeficientes α, identificando de manera iterativa el soporte de la señal hasta alcanzar un criterio de convergencia [19,23]. El algoritmo que lo describe se indica en la Tabla 2.
Otro algoritmo de reconstrucción dispersa empleado en este caso de aplicación de CS es Compressive Sampling Matching Pursuit (CoSaMP) descrito en [24]. El algoritmo aproxima la señal objetivo de forma iterativa y en cada iteración la aproximación actual obtiene un residual actualizando las muestras para que reflejen el residuo actual. Estas muestras se utilizan para identificar los componentes grandes para estimar la aproximación utilizando mínimos cuadrados. Este proceso se repite hasta que se haya encontrado la energía recuperable en la señal. El algoritmo que lo describe se indica en la Tabla 3 [25].
Estos algoritmos son aptos para ser usados en aplicaciones o reconstrucciones donde su funcionamiento se dé en tiempo real debido a su bajo coste computacional.
Debido a que la matriz de sensado debe satisfacer la propiedad RIP, se considera el uso de las matrices de comprobación de paridad usadas en el diseño de codificadores de canal en los códigos LDPC ya que cumplen el criterio de RIP y son deterministas, por ello, consumen menos recursos mostrándose como una buena opción para la matriz de medición en CS [20–22]. Esto permitirá no usar un patrón de pilotos del tipo peine o bloque como es comúnmente utilizado en sistemas OFDM con PSAM. Conforme a esto, se busca usar un patrón de pilotos pseudoaleatorio disperso empleando una matriz de comprobación de paridad LDPC [5].
2.2. Matriz de comprobación de paridad LDPC
La matriz de comprobación de paridad 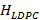 define las relaciones entre los distintos símbolos de codificación (símbolos fuente y símbolos de paridad). Existen dos tipos, las matrices regulares que tienen un número fijo
define las relaciones entre los distintos símbolos de codificación (símbolos fuente y símbolos de paridad). Existen dos tipos, las matrices regulares que tienen un número fijo 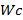 de «1»s lógicos por columnas y un número fijo
de «1»s lógicos por columnas y un número fijo 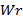 de «1»s lógicos por filas. El segundo es el caso de las matrices irregulares cuyos valores de «1»s lógicos por filas es
de «1»s lógicos por filas. El segundo es el caso de las matrices irregulares cuyos valores de «1»s lógicos por filas es 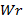 y por columnas
y por columnas  con
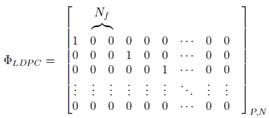
con 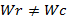 . La matriz está formada por elementos con valores «0» y «1», y es dispersa ya que la mayoría de elementos son nulos [26]. Se describe esta matriz en la Ecuación (9).
. La matriz está formada por elementos con valores «0» y «1», y es dispersa ya que la mayoría de elementos son nulos [26]. Se describe esta matriz en la Ecuación (9).
La matriz 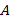 tiene dimensiones
tiene dimensiones 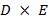 y la matriz
y la matriz 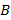 es de
es de 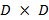 . Donde
. Donde  corresponde a la cantidad de bits de información,
corresponde a la cantidad de bits de información, 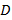 es la cantidad de bits de paridad en la codificación LDPC y
es la cantidad de bits de paridad en la codificación LDPC y 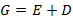 correspondería a la longitud del codeword. Las matrices LDPC regulares se dividen en Gallager caracterizada por una estructura de bandas horizontales [27]. También, en Mackay-Neal caracterizada por una construcción aleatoria [28]. Este tipo de matrices no garantiza una independencia entre columnas necesaria por RIP en CS, por lo cual no se usarán en esta implementación [13].
correspondería a la longitud del codeword. Las matrices LDPC regulares se dividen en Gallager caracterizada por una estructura de bandas horizontales [27]. También, en Mackay-Neal caracterizada por una construcción aleatoria [28]. Este tipo de matrices no garantiza una independencia entre columnas necesaria por RIP en CS, por lo cual no se usarán en esta implementación [13].
Las matrices irregulares se dividen en escalera y triángulo (staircase y triangle) [29]. Son matrices que contienen dos submatrices y cada una de estas un método diferente de creación [29,30]. La submatriz izquierda 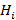 de tamaño
de tamaño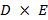 se construye de la siguiente manera:
se construye de la siguiente manera:
Usar un vector en el que conste una lista aleatoria de posibles posiciones de «1»s en las filas. Este vector se utiliza para garantizar una distribución homogénea.
Se coloca en cada columna Wc elementos no cero, escogiendo las posiciones del vector de posibles localizaciones. Si ya no se cumple la condición de máximo Wr elementos no cero por fila se escoge otra posición aleatoria disponible.
Se añade elementos no cero en las filas que tengan menos de dos elementos para evitar problemas en la decodificación.
La submatriz derecha hace la diferencia en la formación de una matriz LDPC irregular ya que se puede formar en escalera o de forma triangular y en cualquier caso es una matriz de dimensión 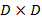 . En el caso de la matriz
. En el caso de la matriz 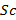 , es una matriz identidad a la que posteriormente se coloca los elementos no cero en la parte inferior diagonal. La Ecuación (10) muestra una matriz
, es una matriz identidad a la que posteriormente se coloca los elementos no cero en la parte inferior diagonal. La Ecuación (10) muestra una matriz 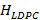 construida mediante este método.
construida mediante este método.
La submatriz derecha triángulo 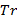 se compone de una matriz identidad como base de dimensión
se compone de una matriz identidad como base de dimensión  , posteriormente se coloca una matriz triangular inferior dispersa. La Ecuación (11) muestra una matriz
, posteriormente se coloca una matriz triangular inferior dispersa. La Ecuación (11) muestra una matriz 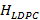 construida mediante este método.
construida mediante este método.
3. Implementación de CS y LDPC para la estimación de canal
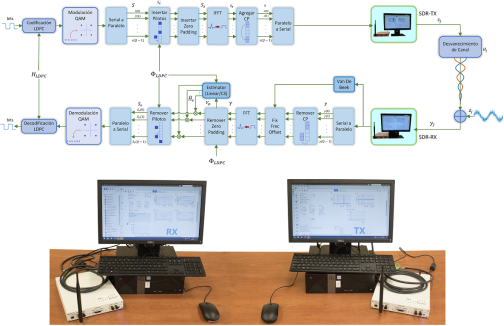
Este trabajo se implementa en equipos periféricos universales de radio por software (USRP, del inglés Universal Software Radio Peripheral). El diagrama de bloques del sistema implementando se puede apreciar en la Figura 2, donde se presenta cada etapa del sistema de comunicación.
Las características de los equipos usados, son los USRP Ettus X310 equivalentes al NI-USRP 2940R con las siguientes especificaciones:
Ancho de banda de hasta 40 MHz por cada canal (2 canales).
La imagen cargada en el FPGA permite conexión Ethernet de 1 Gbps para transmitir 25 MS/s Full Duplex.
La arquitectura UHD usada es la disponible para «LABVIEW Communication Design Suite».
Arquitectura de reloj flexible con frecuencia de muestreo configurable.
El ancho de banda del sistema está en función del índice IQ usado. El índice IQ determina el ancho de banda disponible [31].
Se debe indicar que con el objeto de trabajar con un sistema de comunicaciones más apegado a la realidad, se ha usado un codificador de canal LDPC considerando lo trabajado en [32,33]. La selección de las matrices 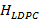 de esta implementación se estableció por validación a través del análisis de BER. La selección de la matriz
de esta implementación se estableció por validación a través del análisis de BER. La selección de la matriz 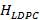 aplicó simulaciones variando la dispersidad de «1»s de la matriz considerando un canal AWGN con desvanecimiento de Rayleigh. Estas matrices tienen un tamaño de
aplicó simulaciones variando la dispersidad de «1»s de la matriz considerando un canal AWGN con desvanecimiento de Rayleigh. Estas matrices tienen un tamaño de  y
y  , debido a su eficiencia y velocidad de acuerdo con la Figura 3. Por esto, la implementación del codificador de canal usa las matrices de verificación de paridad de tipo escalera.
, debido a su eficiencia y velocidad de acuerdo con la Figura 3. Por esto, la implementación del codificador de canal usa las matrices de verificación de paridad de tipo escalera.
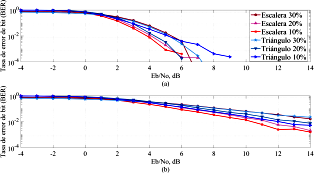
Figura 3. Análisis BER para matrices LDPC irregulares con diferentes porcentajes de dispersión de «1»s: (a) en un canal AWGN. (b) en un canal con desvanecimiento de Rayleigh.
3.1. Estimación de canal basado en CS
En la estimación lineal, el proceso mejora cuando la cantidad de pilotos aumenta a expensas de una reducción del ancho de banda disponible para transmitir información. No obstante, el uso de CS para estimar el canal reduce el número de subportadoras piloto en el proceso es posible ya que solo hay K subportadoras usadas como pilotos. Así, en la Ecuación (12), 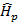 es la versión comprimida del canal. Entonces, el vector comprimido
es la versión comprimida del canal. Entonces, el vector comprimido 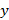 corresponde a
corresponde a  dividiendo los pilotos recibidos
dividiendo los pilotos recibidos 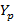 para los enviados
para los enviados 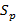 . Por tanto, la matriz de sensado
. Por tanto, la matriz de sensado  es una matriz de tamaño
es una matriz de tamaño 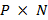 en donde cada
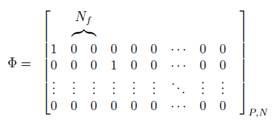
en donde cada  elemento es distinto de 1 y corresponde a la posición de cada símbolo piloto, como se observa en la Ecuación (13) [6]. En una distribución tipo peine
elemento es distinto de 1 y corresponde a la posición de cada símbolo piloto, como se observa en la Ecuación (13) [6]. En una distribución tipo peine 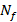 es constante.
es constante.
Para aplicar CS, se consideró un diccionario 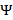 a partir de la DFT para aprovechar el proceso inherente a la IDFT y DFT que se da en OFMD. Los algoritmos de reconstrucción dispersa usados son OMP y CoSaMP, usan como parámetros de entrada los datos comprimidos
a partir de la DFT para aprovechar el proceso inherente a la IDFT y DFT que se da en OFMD. Los algoritmos de reconstrucción dispersa usados son OMP y CoSaMP, usan como parámetros de entrada los datos comprimidos 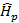 , la matriz
, la matriz 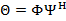 y el total de iteraciones. El número máximo de iteraciones debe estar en relación con el número
y el total de iteraciones. El número máximo de iteraciones debe estar en relación con el número 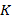 de elementos no cero de la señal a construir, en este caso, el número de portadoras piloto [13]. De esta manera, el canal estimado
de elementos no cero de la señal a construir, en este caso, el número de portadoras piloto [13]. De esta manera, el canal estimado 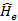 , se obtiene de la forma indicada en la Ecuación (14).
, se obtiene de la forma indicada en la Ecuación (14).
3.2. Estimación de canal con CS y LDPC
Como se indicó en la sección 2, la matriz de sensado 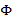 debe cumplir el criterio de RIP para que pueda recuperar adecuadamente la señal dispersa, no obstante, la matriz usada en la Ecuación (13) cumple este criterio en los límites de la restricción ya que no es aleatoria. Por lo tanto, se desarrolla una matriz de posición de pilotos
debe cumplir el criterio de RIP para que pueda recuperar adecuadamente la señal dispersa, no obstante, la matriz usada en la Ecuación (13) cumple este criterio en los límites de la restricción ya que no es aleatoria. Por lo tanto, se desarrolla una matriz de posición de pilotos 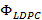 que mejore este requisito. De forma similar a la Ecuación (13), cada elemento no cero corresponde a una posición de cada subportadora piloto en la Ecuación (15) [6].
que mejore este requisito. De forma similar a la Ecuación (13), cada elemento no cero corresponde a una posición de cada subportadora piloto en la Ecuación (15) [6].
La Ecuación (15) mantiene la distancia entre las subportadoras piloto 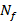 como variable y pseudoaleatoria debido al uso de los algoritmos de LDPC con el que se construye la matriz
como variable y pseudoaleatoria debido al uso de los algoritmos de LDPC con el que se construye la matriz 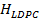 . Para el diseño de
. Para el diseño de 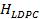 la cantidad de «1»s por fila es igual a 1 tomando en cuenta la cantidad de subportadoras piloto. Además, el porcentaje total de elementos no cero debe ser igual al número de pilotos
la cantidad de «1»s por fila es igual a 1 tomando en cuenta la cantidad de subportadoras piloto. Además, el porcentaje total de elementos no cero debe ser igual al número de pilotos 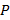 .
.
A partir de la obtención de esta matriz 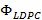 el proceso continúa con la estimación del canal utilizando los algoritmos de reconstrucción dispersa OMP y CoSaMP considerando la distribución de los pilotos obtenidos en
el proceso continúa con la estimación del canal utilizando los algoritmos de reconstrucción dispersa OMP y CoSaMP considerando la distribución de los pilotos obtenidos en  .
.
3.3. Escenarios implementados
Este trabajo aplicó diferentes escenarios manteniendo un enfoque para sistemas Long Term Evolution (LTE). Para esto, se tomó en cuenta las características de LTE tales como el número de subportadoras, símbolos de referencia, subportadoras nulas y la longitud del CP indicadas en [31,34]. Se usó una separación de 7.5 KHz entre subportadoras debido a que con el uso prolongado el rendimiento decae al usar 15 KHz. Entonces el ancho de banda implementado fue de 1.92 MHz. Es necesario aclarar que no se usó un número mayor de subportadoras como si lo permite LTE debido a que el procesamiento del código fuente se dio desde el computador y no sobre el FPGA del equipo.
El primer escenario implementado no usa el codificador de canal y tiene las siguientes características:
IQ sample rate: 1.92 MS/s
Frecuencia de portadora: 1.99 GHz
Modulación: 4 QAM
Iteraciones del algoritmo OMP: 5
Longitud del mensaje transmitido (tren de bits): 1600
Número de muestras en el receptor: 3 × total de datos transmitidos
Total de subportadoras OFDM: 256
Total de subportadoras con datos + pilotos: 150
Ganancia del transmisor: 15.5 - 21 dB
Sensibilidad del receptor: 0 dB
Para obtener los resultados del comportamiento de los estimadores de canal para los diferentes algoritmos de reconstrucción dispersa, OMP y CoSaMP, así como del estimador lineal, se usaron dos SDR por separado ubicados a una distancia considerable en un ambiente cerrado ( indoor) en el laboratorio de pruebas como se observa en la Figura 2. La distancia se consideró como constante y se modificaron las potencias de los equipos para obtener las variaciones de la relación señal a ruido (SNR, del inglés Signal to Noise Ratio) y someter los diferentes estimadores de canal al análisis de BER.
Para el segundo escenario las condiciones anteriores se repiten agregando el codificador de canal LDPC usando las siguientes configuraciones:
El escenario final de análisis se implementa con distancia variable entre transmisor y receptor, también en un ambiente cerrado para evaluar un canal en condiciones más rigurosas. La distancia de separación entre los SDR consideró la longitud, distribución física del laboratorio con distancias entre 4 y 10 metros considerando una potencia constante que no sature el canal.
La variación de distancia permitió recrear canales con gran desvanecimiento, generando un aumento del efecto de multitrayectorias para evaluar el comportamiento de los estimadores. La frecuencia de transmisión es de 2.4 Ghz, por lo que coexiste con la red de wifi del laboratorio, haciendo que el canal varíe constantemente.
En este escenario se trabajó en la presencia de estudiantes utilizando un codificador LDPC manteniendo la siguiente configuración:
IQ sample rate: 1.92 MS/s
Frecuencia de portadora: 2.4 GHz
Modulación: 4 QAM
Iteraciones del algoritmo OMP: 5
Iteraciones del algoritmo de propagación para la decodificación LDPC: 100
Longitud del mensaje transmitido (tren de bits): 1240
Número de muestras en el receptor:
 total de datos transmitidos
total de datos transmitidosNúmero Total de subportadoras OFDM: 256
Número Total de subportadoras con datos + subportadoras piloto: 150
Tipo de matrices LDPC en el codificador: escalera con dispersidad de 1 s entre el 5 al 10 %, 10 al 20 % y 20 al 30 %
Ganancia del transmisor: 20 dB
Sensibilidad del receptor: 20 dB
4. Análisis de resultados
4.1. Escenarios 1 y 2 - Análisis de BER
En la implementación del algoritmo OMP, el número de interacciones debe ser elegido de forma que K corresponda al número de elementos diferentes de cero de la señal que se busca recuperar. Para definir este valor, se desarrollaron múltiples pruebas buscando minimizar el error en la estimación de canal obteniendo que el valor adecuado para que este algoritmo converja en la implementación es de K = 5 correspondiente al número mínimo de subportadoras usado.
La Figura 4 muestra el comportamiento de BER con 5 y 25 subportadoras piloto para los estimadores basados en OMP, CoSaMP y el estimador lineal para el primer escenario.
En la Figura 4 se puede observar que a bajos niveles de SNR el estimador lineal presenta un rendimiento menor con respecto al uso de los estimadores basados en el paradigma de CS empleados. Con 25 subportadoras piloto, los estimadores de canal alcanzan una reducción considerable en la probabilidad de pérdida de bits. En estas pruebas los algoritmos de CoSaMP y OMP trabajaron con la matriz 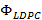 y en ausencia de esta (distribución de subportadoras piloto de tipo peine).
y en ausencia de esta (distribución de subportadoras piloto de tipo peine).
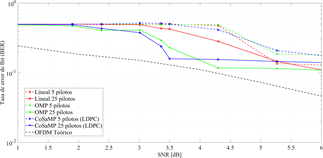
La Figura 5 muestra el comportamiento de BER para 5 estimadores de canal usando las configuraciones del segundo escenario. Entonces, la Figura 5(a) de acuerdo con lo esperado por el uso de un codificador de canal, puede observarse una clara mejora respecto del caso anterior. El estimador lineal tiene los peores resultados ante un SNR bajo. Por otra parte, los estimadores CoSaMP tienen un rendimiento similar usando o no la matriz 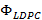 . No obstante, la versión con matriz
. No obstante, la versión con matriz 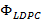 presenta un mejor rendimiento. También, a medida que mejora el SNR, el estimador CoSaMP sin matriz
presenta un mejor rendimiento. También, a medida que mejora el SNR, el estimador CoSaMP sin matriz 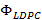 tiene una ligera mejora, pero continuando ambos con la misma tendencia en su comportamiento. Los estimadores OMP por su parte, presentan un menor rendimiento contrastados con CoSaMP, teniendo en cuenta que la versión con la matriz
tiene una ligera mejora, pero continuando ambos con la misma tendencia en su comportamiento. Los estimadores OMP por su parte, presentan un menor rendimiento contrastados con CoSaMP, teniendo en cuenta que la versión con la matriz  es la que peores resultados ofrece en particular para este algoritmo.
es la que peores resultados ofrece en particular para este algoritmo.
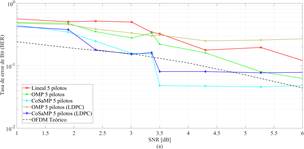
La Figura 5(b) muestra resultados del rendimiento de los estimadores frente al BER usando 25 subportadoras pilotos para cada uno. Se puede observar que el estimador lineal presenta mayor probabilidad de error de bit para un bajo SNR, mostrando el peor comportamiento de entre todos los estimadores analizados. Sin embargo, cuando el SNR supera a priori el valor de 3.5 dB su rendimiento aumenta, obteniendo la menor probabilidad de error de bit frente a los otros estimadores.
4.2. Escenario 3 – Análisis para distancias variables
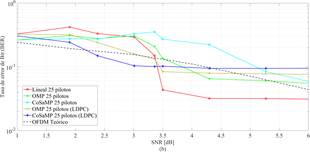
Las Figuras 6 y 7 corresponden al comportamiento del estimador lineal y de los estimadores basados en CS con y sin la matriz 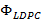 .
.
La Figura 6 muestra que el estimador lineal tiene un mejor comportamiento a muy corta distancia, lo que corresponde a los resultados anteriores en el análisis de BER. No obstante, a medida que la distancia aumenta, este estimador de canal reduce su rendimiento en forma drástica. El estimador CoSaMP con 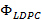 es mejor en contraste con lo que sucede con el estimador que usa OMP. Se debe indicar que esta figura toma en cuenta los resultados ante el uso de 5 a 25 subportadoras piloto.
es mejor en contraste con lo que sucede con el estimador que usa OMP. Se debe indicar que esta figura toma en cuenta los resultados ante el uso de 5 a 25 subportadoras piloto.
Debido a que el decodificador de canal usa como entrada las respuestas de los estimadores de canal, en este escenario se analizó el porcentaje de valores que de dicho codificador no pudo resolver. De esta manera, la Figura 7 muestra el porcentaje de valores nulos (NaN) en contraste con los cambios de distancia para cada estimador de canal.
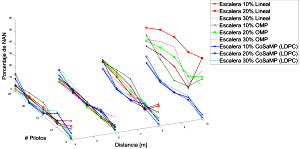
Figura 7. Análisis de la convergencia del decodificador de canal según la respuesta de los estimadores a diversas distancias.
La Figura 7 también corrobora los resultados anteriores resaltando la misma tendencia en los estimadores. El estimador lineal trabaja mejor a distancias cortas y los estimadores CS tienen mejor rendimiento que el lineal frente a canales ruidosos, comprobándose esto al aumentar la distancia.
4.3. Análisis del ancho de banda
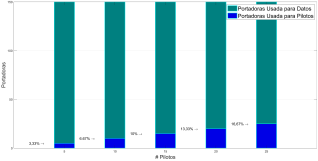
La Figura 8 muestra la relación que existe entre el ancho de banda usado por las subportadoras piloto y el ancho de banda para el envío de información en un símbolo OFDM. De este modo, usar 5 subportadoras piloto en lugar de 25, corresponde a una mejora de eficiencia espectral del 13.33 %. Esta mejora espectral corresponde al uso de los estimadores de canal basados en CS como se ve en la Figura 8.
5. Conclusiones
De acuerdo con los resultados obtenidos, los estimadores CoSaMP presentan un mejor rendimiento para bajos niveles de SNR con el uso de la matriz 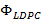 . Los estimadores OMP muestran un comportamiento similar al CoSaMP aunque con menor rendimiento. Así, con los resultados obtenidos se deduce que, un estimador lineal trabaja el problema de la estimación de canal con muy baja complejidad computacional. No obstante, cuando el canal es muy ruidoso sobre todo debido a multitrayectos demanda mayor cantidad de subportadoras piloto para tratar de mantener su rendimiento, lo que significa reducción del ancho de banda efectivo. En contraste, los estimadores que basados en CS usados en este trabajo, además de mantener baja complejidad computacional, para canales ruidosos muestran un rendimiento adecuado, permitiendo la transferencia de datos en canales ruidosos, considerando que se evaluó en un ambiente indoor.
. Los estimadores OMP muestran un comportamiento similar al CoSaMP aunque con menor rendimiento. Así, con los resultados obtenidos se deduce que, un estimador lineal trabaja el problema de la estimación de canal con muy baja complejidad computacional. No obstante, cuando el canal es muy ruidoso sobre todo debido a multitrayectos demanda mayor cantidad de subportadoras piloto para tratar de mantener su rendimiento, lo que significa reducción del ancho de banda efectivo. En contraste, los estimadores que basados en CS usados en este trabajo, además de mantener baja complejidad computacional, para canales ruidosos muestran un rendimiento adecuado, permitiendo la transferencia de datos en canales ruidosos, considerando que se evaluó en un ambiente indoor.
El uso del paradigma de CS mejora mientras las propiedades de RIP y de espacio nulo puedan asegurarse, en este caso, el canal se puede considerar como disperso porque el número de subportadoras piloto es disperso.
Además, implementar una matriz de sensado diseñada a partir de la conceptualización de las matrices LDPC ha permitido mejorar el comportamiento de los estimadores basados en CS, la mejora es más clara para el estimador que usa OMP. El estimador CoSaMP con 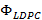 muestra ser el mejor estimador frente a esta problemática de trabajo en conjunto con el codificador de canal usado. Entre los trabajos a futuro es implementar la estimación de canal y procesamientos previos en el FPGA del dispositivo para permitir que la comunicación entre el equipo y la fuente de datos pueda usar una mayor tasa de transmisión de datos.
muestra ser el mejor estimador frente a esta problemática de trabajo en conjunto con el codificador de canal usado. Entre los trabajos a futuro es implementar la estimación de canal y procesamientos previos en el FPGA del dispositivo para permitir que la comunicación entre el equipo y la fuente de datos pueda usar una mayor tasa de transmisión de datos.