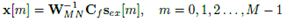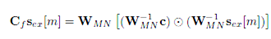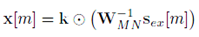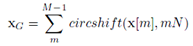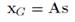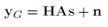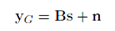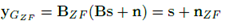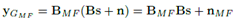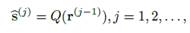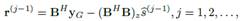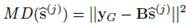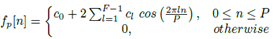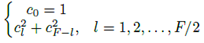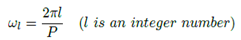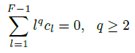Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Similars in
SciELO 
Permalink
1. Introducción
Las comunicaciones inalámbricas y móviles se han convertido en herramientas esenciales para la vida y la sociedad moderna. Las redes de telecomunicación del futuro necesitan un mayor rendimiento sobre la base de eficiencias espectral y energética muy elevadas, latencia muy pequeña y velocidades de datos muy altas. Para esto se requiere una capa física (PHY) más efectiva [1–3]. La esencia de la capa física de las redes de cuarta generación (4G) es la multiplexación por división en frecuencias ortogonales (OFDM, Orthogonal Frequency Division Multiplexing). Estos sistemas permiten alcanzar un alto rendimiento de datos. La modulación OFDM es ampliamente utilizada debido a sus características favorables como implementación sencilla basada en la transformada rápida de Fourier (FFT, Fast Fourier Transform), y robustez contra canales con desvanecimiento [2, 4]. Sin embargo, el escenario de aplicación que se ha previsualizado para las redes de quinta generación (5G) posee retos donde la modulación OFDM podría tener limitaciones. La baja latencia que se necesita para las comunicaciones vehículo a vehículo y las aplicaciones táctiles de Internet requieren un umbral de datos donde el paquete OFDM con un prefijo cíclico (CP, Cyclic Prefix) por símbolo tiene una baja eficiencia espectral [1, 4–6].
El requerimiento de OFDM de preservar la ortogonalidad entre subportadoras individuales es esencial para la comunicación máquina a máquina (M2M, Machine-to-Machine). Dada la necesidad de bajo consumo de potencia que influye en forma negativa en el proceso de sincronización, este procedimiento no es posible con la modulación OFDM [4, 7]. Otra desventaja del sistema OFDM es la alta radiación fuera de banda (OOB, out-of-band) que resulta de la forma rectangular del pulso [8]. Debido a estas deficiencias, OFDM puede satisfacer los requerimientos del 5G de forma limitada.
En los últimos años se han propuesto diferentes formas de onda para superar las limitaciones previamente citadas de OFDM; tal es el caso de FBMC, UFMC y GFDM en las referencias [9–14], en las que se sugieren numerosas formas de onda. En la multiportadora de banco de filtros (FBMC, Filter Bank Multicarrier) se da forma a los pulsos de las subportadoras individualmente para reducir las emisiones OOB, causadas por el ancho de banda angosto de las subportadoras, y por la larga longitud de la respuesta al impulso del filtro transmisor. Las aplicaciones que necesitan transmitir un número grande de símbolos sacan provecho de esta modulación. Sin embargo, está claro que este esquema de modulación no es apropiado para escenarios de baja latencia, donde debe alcanzarse alta eficiencia con la transmisión de ráfagas cortas [1, 5–7]. En la multiportadora filtrada de manera universal (UFMC, Universal Filtered Multicarrier) se filtra un grupo de subportadoras para reducir la emisión OOB. La característica principal de esta modulación es que la respuesta al impulso puede ser corta, obteniendo alta eficiencia espectral en transmisiones cortas [1].
La desventaja de UFMC es que no requiere un CP, por lo que es más sensible que CP-OFDM a la desalineación de tiempo corto, y podría no ser apropiado para aplicaciones que necesitan un tiempo largo de sincronización con el fin de ahorrar energía [1, 5, 6]. En este contexto, la multiplexación por división en frecuencias generalizadas (GFDM, Generalized Frequency Division Multiplexing) es una alternativa de esquema multiportadora que está siendo evaluada actualmente como una candidata de capa PHY para la próxima generación de sistemas de comunicaciones móviles. Es interesante notar que la importancia de la GFDM es ser una forma generalizada de la OFDM que preserva la mayoría de sus valiosas propiedades, mientras aborda sus limitaciones. La GFDM puede ofrecer una radiación OOB muy baja. Además, es más eficiente que la OFDM en ancho de banda, ya que utiliza un solo CP para un grupo de símbolos en un bloque, en vez de un CP por símbolo como en el caso de la OFDM [9, 15].
La modulación GFDM está concebida para la modulación de bloques independientes, donde cada bloque consiste de un número de subportadoras y símbolos. Los símbolos de datos pertenecientes a las subportadoras son filtros con un prototipo que es desplazado circularmente en los dominios del tiempo y de la frecuencia. El filtrado de las subportadoras resulta en subportadoras no ortogonales, lo que podría producir interferencias entre símbolos (ISI, Inter Symbol Interference) y entre portadoras (ICI, Inter Carrier Interference). La respuesta impulso del filtro (FIR, Filter Impulse Response) puede ser utilizada para filtrar las subportadoras, y esta opción tiene un impacto negativo en el desempeño de la tasa de error binario (BER, Bit Error Rate) y en las emisiones OOB, como se muestra en [1]. En este trabajo se presentan curvas de BER para comparar la influencia que tiene la selección del número total de coeficientes del filtro en los sistemas GFDM. Es necesario presentar este aspecto porque el desempeño se degrada cuando el número total de coeficientes no se elige correctamente.
Un símbolo GFDM consiste de una estructura de bloque con MN muestras, donde cada subportadora N transporta M intervalos de tiempo. En un bloque GFDM, la sobrecarga se mantiene pequeña agregando un único CP para un bloque completo que contiene múltiples subportadoras. De este modo, puede utilizarse un período que ayude a mejorar la eficiencia espectral del sistema. Las secciones restantes se organizan de la siguiente manera. El modelo del sistema y las propiedades del transmisor GFDM se presentan en la Sección 2. La Sección 3 presenta diferentes estructuras de receptor. La Sección 4 muestra la expresión del filtro prototipo que se obtiene de los coeficientes del filtro de subportadora. La Sección 5 analiza el desempeño de la BER en la GFDM, incluyendo las ecuaciones teóricas suponiendo receptores sin impulso (ZF, Zero-Forcing), filtro adaptado (MF, Matched Filter) y filtro adaptado con cancelación de interferencia paralela (MF-PIC, Matched Filter–Parallel Interference Cancellation). Se tilizaron los coeficientes obtenidos Importar tabla
en la Sección 4. Finalmente, la Sección 6 presenta algunas conclusiones. El objetivo principal de este trabajo es presentar una estructura para la GFDM aprovechando el arreglo en la matriz de modulación.
Notación: Se utiliza minúscula en negrita para los vectores columna y mayúscula en negrita para las matrices. Todos los vectores están en forma de columna. La transpuesta y la hermítica de vectores y matrices se indican por los superíndices ‘T’ y ‘H’, respectivamente. Se utiliza W
MN
para denotar la matriz transformada discreta de Fourier (DFT, Discrete Fourier Transform) de tamaño MN. Asimismo, se supone que W
MN
está normalizada, tal que W
MN
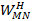= I
MN
, donde I
MN
denota la matriz identidad de tamaño MN. Por lo tanto, 
= 
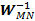. Los términos FFT e iFFT se refieren a la implementación rápida de la DFT y la DFT inversa (iDFT), respectivamente.
2. Materiales y métodos
2.1. Modelo del sistema y propiedades del GFDM
La multiplexación por división en frecuencias generalizadas (GFDM) es un sistema multiportador. El paquete de datos en la GDFM es tal que solo se requiere un CP por bloque de símbolos transmitidos [10 ]. La Figura 1 presenta la estructura de un paquete de datos GDFM. En el sistema GFDM los símbolos de datos sobre cada subportadora se filtran a través de un filtro pasabanda bien localizado, con la finalidad de limitar la interferencia entre portadoras (ICI) [16]. El paquete de datos del GDFM está organizado en M intervalos de tiempo y M subportadoras.
El sistema OFDM puede producir alta radiación fuera de banda (OOB) y una menor eficiencia en ancho de banda en comparación con GFDM [1,8] debido al hecho de que el sistema OFDM utiliza un CP por símbolo, como se presenta en la Figura 2
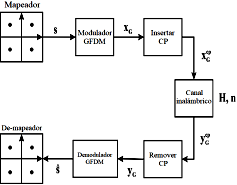
Considere el diagrama de bloques del transceptor mostrado en la Figura 3. Un mapeador, por ejemplo, QAM [7], mapea los bits codificados a símbolos de una constelación compleja de 2α valores, donde α es el orden de la modulación. El vector s denota un bloque de datos que contiene MN símbolos, que puede descomponerse en M intervalos de tiempo y N subportadoras, cada una de acuerdo con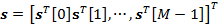 
y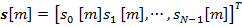 
, 
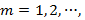
Los símbolos de los datos son tomados de un proceso independiente e idénticamente distribuido (i.i.d.) de media cero y varianza unitaria. La expresión que relaciona los símbolos de los datos de entrada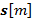 
y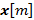 
la salida del transmisor GFDM, puede expresarse como [16].
donde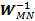 
es la matriz iDFT de tamaño 
, 
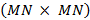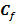es una matriz circular de tamaño 
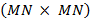, con la primera columna constituida por el vector 
. Los coeficientes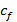 
son los componentes del espectro discreto del pulso que establece el formato, con 
y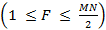 
[17, 18]. En este trabajo se mostrará que la cantidad de coeficientes influye en el desempeño del sistema GFDM; 
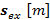es el vector expandido 
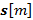de símbolos de datos que puede ser organizado como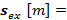 
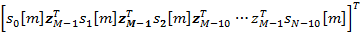, donde 
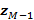representan un vector columna de tamaño 
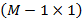[17, 18].
La expresión (1) se implementa en dos pasos. Primero se ejecuta la convolución circular de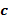 
y 
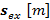Posteriormente se aplica una iFFT de tamaño 
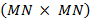al resultado del primer paso, para obtener el vector 
de tamaño 
.
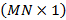Es útil comentar que la complejidad computacional representada por (1) está determinada de manera dominante por una iFFT de dimensión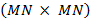 
. El resultado 
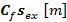puede calcularse como:
donde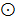 
es un operador que denota multiplicación punto a punto, y la convolución circular de los vectores 
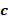y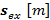 
se realiza a través de la multiplicación punto a punto de sus respectivas iDFTs y posteriormente se aplica una DFT al resultado. Si se consideran las expresiones (1) y (2) el vector 
se reduce a:
donde 
es el vector de los coeficientes del filtro prototipo que influyen en el desempeño del GFDM. La complejidad computacional de (3) puede reducirse significativamente tomando en consideración que el vector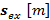 
es la versión expandida del vector de símbolos. Sin embargo, el producto 
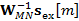puede obtenerse a través de 
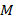repeticiones de 
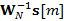en una columna. Entonces la complejidad computacional en (3) puede calcularse a través de una iFFT de dimensión 
.
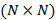Los símbolos de datos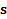 
del paquete GFDM a ser transmitido, que se muestra en la Figura 2, pueden obtenerse mediante la superposición de los 
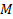vectores 
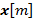. Esta operación puede describirse matemáticamente como:
donde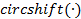 
significa desplazamiento circular descendente. El paquete a ser transmitido se completa agregando las CP muestras para obtener el vector 
. Un modelo interesante de un sistema GFDM es un modelo matricial con el objetivo de tener similitud con el sistema OFDM. El modelo presentado en [17-
22] y el vector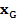 
puede ser expresado en forma matricial como:
donde 
es el vector columna que contiene todos los símbolos de datos del paquete GFDM de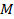 
intervalos de tiempo y 
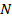subportadoras, como se ilustra en la Figura 2. 
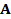es la matriz del sistema GFDM que está compuesta por los coeficientes 
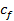del filtro prototipo que afectan el desempeño del sistema. Los coeficientes 
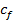serán calculados en otra sección.
2.2. Implementación del receptor
El vector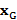 
es la salida del modulador GFDM (ver Figura 3), y 
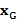contiene las muestras transmitidas que corresponden al bloque de datos 
del GFDM de tamaño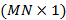 
. Finalmente, se agregó en el lado del transmisor un prefijo cíclico de 
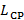muestras para producir 
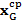. Posteriormente la señal es afectada por Ruido Blanco Gaussiano Aditivo (AGWN, Additive Gaussian White Noise),
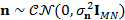, donde 
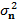es la varianza del ruido. La señal del receptor luego de remover CP muestras puede expresarse como:
donde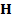 
representa la matriz circular del canal de tamaño 
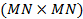. La primera columna está determinada por el vector 
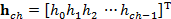que corresponde a la respuesta al impulso del filtro pasa-bajo discreto de tamaño 
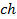(completado con ceros) equivalente al canal. La matriz circular 
puede expresarse como:
A partir de la matriz representada por la ecuación (7), pueden utilizarse dos tipos de receptores GFDM estándar, es decir, Sin Impulso (ZF) y Filtro Adaptado (Matched Filter, MF) [4], [22, 23]. Se ha definido la matriz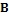 
como el producto de 
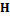y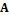 
. Entonces, la ecuación (6) puede reescribirse como:
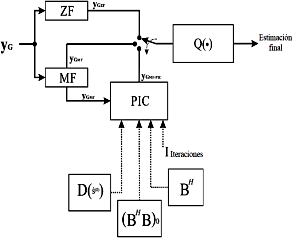
El esquema de ecualización utilizado en este trabajo se presenta en la Figura 4. En el diagrama de bloques, 
es una función que relaciona cada componente del vector de la señal transmitida con el símbolo más cercano a la constelación de la señal de la modulación utilizada y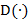 
determina la distancia mínima de acuerdo a la métrica utilizada en el detector PIC. El interruptor en la figura define el receptor empleado en cada estado para obtener el estimado final. Aquí ZF y MF son detectores lineales y PIC es el detector de Cancelación de Interferencia Paralela (Parallel Interference Cancellation). Por lo tanto, el PIC se utiliza como una primera estimación de la señal de salida del bloque MF.
El receptor ZF se caracteriza por la matriz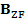 
, que representa la inversa de la matriz 
. Después de obtener la ecualización ZF, la demodulación lineal de la señal recibida puede expresarse como:
donde 
es el ruido después de la ecualización ZF que afecta la señal recibida de tamaño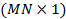 
.
El segundo tipo de receptor, el MF, es descrito por la matriz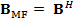 
. Cuando se aplica al vector recibido en (8), la señal recibida puede expresarse como:
donde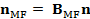 
es el ruido después de la ecualización MF de tamaño 
.
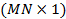La implementación del detector PIC presenta la menor complejidad computacional, en comparación con otros detectores de cancelación como SIC [17- 20]. La primera estimación de los símbolos de datos al detector PIC se obtiene como la señal de salida del detector MF. Este receptor puede implementarse por las ecuaciones:
donde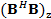 
corresponde a la matriz 
con ceros en la diagonal principal.
Las estimaciones de símbolos utilizando las ecuaciones (11) y (12) son generadas secuencialmente hasta un número máximo de J iteraciones. En el presente trabajo se consideró que el proceso puede ser interrumpido después de la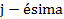 
iteración 
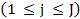dependiendo de la calidad de los estimados generados. La métrica de Máxima Verosimilitud (ML, Maximum Likelihood) empleada aquí corresponde a la métrica de Mínima Distancia (MD). Puede calcularse como:
i se detecta una reducción en la calidad de un estimado dado, esto es,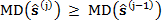 
, el estimado 
es adoptado como el final.
2.3. Cálculo de los Coeficientes de los Filtros de las Subportadoras
El filtrado de las subportadoras en el bloque modulador GFDM que se presenta en la Figura 3 es esencial para el desempeño del sistema. En esta sección se presenta cómo determinar sus coeficientes. El filtro prototipo que se presenta en [16, 24 - 26], corresponde a una clase de filtros pasa-bajo reales cuya respuesta al impulso puede expresarse como:
donde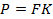 
, y 
son coeficientes reales, el factor 
de solapamiento es un entero positivo y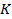 
es el número de canales en el sistema TMUX. De acuerdo a Mirabbasi y Martin [25], los coeficientes 
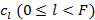, deben satisfacer las siguientes condiciones:
Si los coeficientes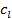 
son seleccionados tal que (15) se satisfaga, entonces la frecuencia de 
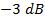del filtro prototipo sería aproximadamente 
, cuando 
es par. La mínima atenuación en la banda rechazada (MSA, Minimum Stopband Attenuation) y la tasa aproximada de decaimiento (ARF, Approximate Rate of Fall-Off) de los lóbulos laterales dependen del factor F de solapamiento y son independientes del orden del filtro [25].
Se requiere determinar los coeficientes 
de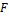 
resolviendo un sistema. En [24] se obtuvo la ecuación auxiliar:
Si se satisface la ecuación (16), entonces los lóbulos laterales de la transformada discreta de Fourier en la ecuación (14) tienen la tasa aproximada de decaimiento (fall-off rate) de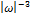 
, con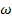 
definiendo las frecuencias uniformemente espaciadas alrededor del círculo unitario. Esto puede escribirse como:
Mediante las ecuaciones (15) y (16) es posible construir un sistema de ecuaciones con el mismo número de incógnitas. Además, la ecuación (18) puede utilizarse para construir las ecuaciones restantes necesarias para tener un sistema de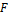 
ecuaciones.
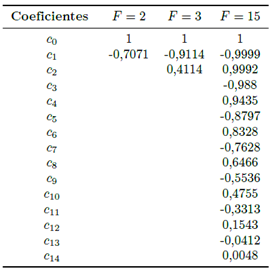
Con las ecuaciones previas es posible obtener los valores de los coeficientes del filtro prototipo para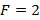 
, 
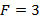y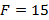 
. Éstos se muestran en la Tabla 1.
3. Resultados y Discusión
Esta sección presenta los resultados de las simulaciones junto con las expresiones teóricas obtenidas. Con el fin de estudiar el efecto en la BER del número de coeficientes del filtro de las subportadoras en el sistema GFDM, se ha considerado en caso de los receptores ZF, MF y MF-PIC.
3.1. Análisis de la Tasa de Error Binario (BER)
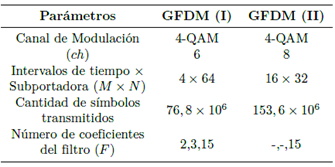
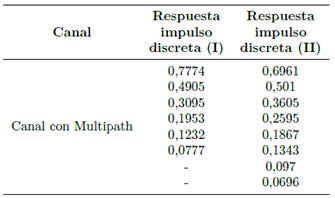
En esta subsección se analiza el desempeño del sistema GFDM en términos de la BER vs.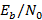 
, suponiendo que se utilizan ZF, MF y MF-PIC. El ZF es capaz de remover la generación propia de interferencia, al costo de introducir un aumento del ruido [1]. El receptor MF-PIC fue el más flexible y adaptable a diferentes configuraciones del paquete de datos GFDM [17], [18], como se describe en la Figura 1. La Tabla 2 presenta los parámetros del sistema utilizados en la simulación, mientras que la Tabla 3 muestra la respuesta impulso del canal que fue utilizada en la evaluación del desempeño de la BER. La respuesta impulso del canal con múltiples trayectorias (multipath) se normaliza para tener energía unitaria, y la longitud de la banda de guarda CP es 
.
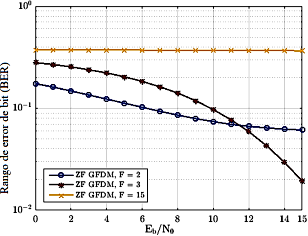
La Figura 5 compara el desempeño de la BER del ZF clásico en el sistema GFDM con diferentes números de coeficientes del filtro de las subportadoras, considerando los parámetros del sistema de la Tabla 2 y el canal con multipath de la Tabla 3. Los resultados presentados en la Figura 5 sugieren que el sistema GFDM logró el mejor desempeño cuando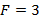 
. En este caso la BER estuvo en el orden de 
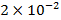cuando se compara con los resultados presentados para 
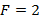, mientras que 
tuvo más de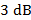 
de ventaja.
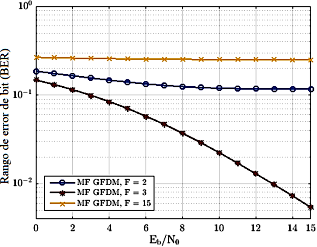
Las Figuras 6 y 7 ilustran el desempeño de la BER para los receptores MF y MF-PIC, respectivamente, considerando los tres casos de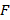 
. Las figuras muestran que el desempeño del sistema GFDM depende fuertemente del número de coeficientes del filtro prototipo de las subportadoras. El caso 
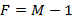representó la mejor opción de número de coeficientes del filtro en el sistema GFDM. Aquí 
representa los intervalos de tiempo del sistema, como se muestra en la Figura 2.
Los resultados mostrados en la Figura 8 sugieren que utilizando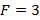 
para los diferentes receptores, el detector MF-PIC tuvo el mejor desempeño del sistema GFDM. Se encontró que el receptor MF es 
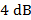más eficiente que el ZF, con menor complejidad computacional. El MF-PIC es más complejo que ZF y MF debido al número de iteraciones [18]. Además, en la Figura 8 se presentan (como una comparación) dos curvas de desempeño, una 4-QAM teórica y otra ZF CP-OFDM con 64 FFT. Se encontró que el desempeño de la BER del esquema MF-PIC es aproximadamente igual al del ZF CP-OFDM FFT 64, con una diferencia de 0,5 dB a favor del sistema CP-OFDM. La causa de esta pequeña diferencia es que el sistema GFDM es afectado por la matriz de transmisión, que depende del número de coeficientes. Sin embargo, ambos sistemas tienen la misma complejidad computacional en la generación de la señal ya que necesitan FFT 64, pero el GFDM es más eficiente que OFDM en términos de espectro porque sólo necesita un CP para transmitir un paquete de datos de 256 símbolos. Por otra parte, la gran diferencia en el desempeño de la BER del 4-QAM es producida porque se considera como un sistema con AWGN.
En las simulaciones ambos sistemas tienen la misma complejidad computacional en la generación de la señal ya que ambos necesitan FFT 64, pero el GFDM es más eficiente que OFDM en términos del espectro porque sólo necesita un CP para transmitir un paquete de datos de 256 símbolos.
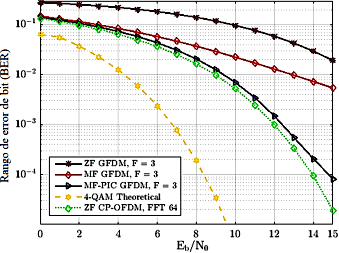
Figura 8 Comparación de los resultados de las simulaciones para los receptores ZF, MF y MF-PIC en GFDM (I) con F = 3 , 4-QAM teórico y ZF CP-OFDM FFT 64, canal I.
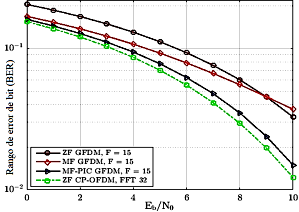
La Figura 9 presenta otras simulaciones considerando que el sistema GFDM tiene matrices de dimensión 
y las propiedades descritas en la Tabla 2 para GFDM (II). Las respuestas impulso del canal tienen 8 tomas como se muestra en la Tabla 3. La Figura 9 muestra que el desempeño del esquema detector MF-PIC es aproximadamente el mismo que con ZF CP-OFDM FFT 32, con una diferencia en el desempeño de 0,5 dB a favor del sistema CP-OFDM. Aquí es posible verificar nuevamente que existe una relación intrínseca con el total de coeficientes del filtro de la subportadora, porque el mejor desempeño que puede alcanzar el sistema GFDM es igual al del sistema OFDM. La degradación del desempeño en la Figura 9 en comparación con la Figura 8 está dada por el efecto del canal por el incremento en el número de tomas.
4. Conclusiones
Los escenarios de implementación esperados para las redes inalámbricas 5G plantean retos, ya que las tecnologías disponibles de capa física exhiben un desempeño limitado debido a sus deficiencias. El sistema GFDM parece un candidato útil por su rendimiento con el sistema OFDM. La propiedad clave del sistema GFDM es su flexibilidad, tal que diferentes aplicaciones pueden tener una solución simple. De esta manera, es importante garantizar la coexistencia con otras tecnologías, como la 4G actual.
Se produjeron esquemas de modulación y demodulación para el sistema GFDM. Los esquemas presentados tienen una estructura matricial que reduce la complejidad computacional, sin incurrir en ninguna penalización por deterioro del desempeño. Utilizando la estructura matricial del transmisor y del receptor de los sistemas GFDM, se analizó y comparó el desempeño en la BER para los diferentes coeficientes calculados. Se mostró que el desempeño de la BER en el sistema GFDM depende del número de coeficientes del filtro y del filtro prototipo. En el sistema GFDM, el incremento del número total de coeficientes del filtro no mejora el desempeño. El total de coeficientes depende del número de subportadoras, porque podría filtrar símbolos de otros paquetes y generar interferencia. El desempeño del sistema está condicionado por el número preciso de coeficientes.
