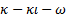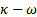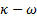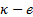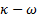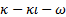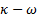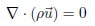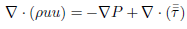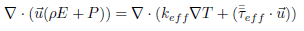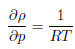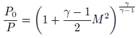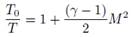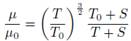1. Introducción
Estudios experimentales del comportamiento del flujo compresible a velocidades supersónicas, son realizados en toberas con diferentes geometrías en las secciones divergentes, tales como: de secciones transversales circulares, ovaladas, rectangulares, entre otras. Cuando se produce un cambio brusco de la presión del flujo en la sección divergente de la tobera, se presenta la onda de choque, por tanto, las propiedades del fluido, temperatura, velocidad, densidad, entre otros, varían a consecuencia de la descompresión y compresión del flujo. En el análisis de este tipo de flujo el número de Mach es el parámetro dominante.
Una manera de captar la forma de la onda de choque, las turbulencias y la separación del flujo de las paredes de una tobera, es mediante la técnica Schlieren. Esta capta imágenes de la variación de la densidad mediante un proceso óptico, y fue propuesta por el físico alemán August Toepler en 1864 [1], quien fue el primero en visualizar la forma de la onda; y esta técnica es empleada de manera recurrente en el campo del flujo a alta velocidad.
Las imágenes y parámetros físicos del flujo compresible obtenidos en laboratorio son de gran importancia para conocer la naturaleza del mismo, cuando el flujo es sometido a diferentes variaciones de presión y temperatura. Pues, las magnitudes de los parámetros físicos son obtenidas por observación directa, y las magnitudes de otras propiedades termodinámicas que no pueden ser obtenidas por observación directa son obtenidas mediante el empleo de ecuaciones empíricas o modelos matemáticos.
En la literatura, están sustentados y reportados trabajos sobre la capa límite de flujo compresible [2]; la capa límite con diferentes condiciones de gradiente de presión [3]; de ondas de choque normal, oblicuas, ondas expansivas de Prandtl-Meyer [4,5]; y la turbulencia [6].
El comportamiento del flujo compresible puede ser reproducido empleando códigos de la dinámica de fluidos computacional (DFC, CFD por sus siglas en inglés) [7, 8], las cuales emplean modelos matemáticos de ecuaciones gobernantes y modelos de turbulencia [9] acoplados en la ecuación de cantidad de movimiento.
De las diferentes geometrías de toberas experimentales de laboratorio, se ha motivado a estudiar el flujo compresible para una tobera plana, cuya imagen de la geometría se muestra en la Figura 1, la cual fue tomada del trabajo de Hunter [10].
Basado en la teoría en una dimensión, la tobera plana que se expone en la imagen, tiene un ángulo medio de la sección divergente de 11,01 °, la cual es considerada una tobera fuera de diseño con respecto a su geometría. Esta tobera fue diseñado para una relación de presión rp = 8, 78, en la salida de la sección divergente para número de Mach 2,07 y presión 102,387 kPa (14,85 psi), en la entrada de la sección convergente para la temperatura de estancamiento de 294,444 K (530 °R), en la garganta para número de Reynolds 3, 2 × 106 [10].
Cabe señalar, típicamente, el ángulo medio de diseño en la sección divergente para toberas cónicas se encuentra en el rango de 12-18° [11] y se aplica el mismo principio para toberas planas.
Hunter [10] reportó en su trabajo resultados experimentales de presión estática tomados en la pared de la tobera plana, para el rango de relaciones de presión rp = 1, 255 − 9, 543. Además, simuló el flujo de aire para la geometría de la tobera plana, empleando tres modelos de turbulencia: el de Shih-Zhu-Lumley (SZL) [12] Gatski-Speziale (GS) [13] y de Girimaji [14], los cuales, comparó con los datos experimentales de presión, para rp = 3, y sustentó que el modelo de turbulencia SZL presenta mejores resultados con respecto a los otros dos modelos de turbulencia empleados.
Balabel [15] simuló el flujo para la geometría de la tobera plana [10], con los modelos de turbulencia: k-e estándar [16], k − e extendido [17], v2 − f [18], v2 − f realizable [19], SST k − 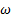 [20] y RSM [21], y comparó las curvas numéricas obtenidas con datos experimentales de presión estática para rp = 1, 255, rp = 2, 412 y rp = 5, 423. Además, simuló el flujo empleando el modelo de turbulencia SST para un bajo y alto número de Reynolds, también comparando con datos experimentales para rp = 2, 412 y rp = 5, 423. De sus resultados, consideró que el modelo de turbulencia SST k −
[20] y RSM [21], y comparó las curvas numéricas obtenidas con datos experimentales de presión estática para rp = 1, 255, rp = 2, 412 y rp = 5, 423. Además, simuló el flujo empleando el modelo de turbulencia SST para un bajo y alto número de Reynolds, también comparando con datos experimentales para rp = 2, 412 y rp = 5, 423. De sus resultados, consideró que el modelo de turbulencia SST k − 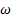 tiene mayor cercanía con los datos experimentales.
tiene mayor cercanía con los datos experimentales.
Además, la geometría de la tobera plana [10] también fue empleada por Toufique [22], quien simuló el flujo con el modelo de turbulencia k − 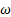 estándar [23], comparando las formas de las ondas de choque obtenidas con datos experimentales, para rp = 2, 4 y rp = 3, 0, donde se muestra que el ancho del disco de Mach es ligeramente menor al disco de Mach experimental. También, Kotteda et al. [23] estudiaron el flujo para diferentes relaciones de presión y relaciones de área, simulando el flujo en 2D con el modelo de turbulencia Sparlat-Allmaras, obteniendo diferentes configuraciones de la forma de ondas de choque.
estándar [23], comparando las formas de las ondas de choque obtenidas con datos experimentales, para rp = 2, 4 y rp = 3, 0, donde se muestra que el ancho del disco de Mach es ligeramente menor al disco de Mach experimental. También, Kotteda et al. [23] estudiaron el flujo para diferentes relaciones de presión y relaciones de área, simulando el flujo en 2D con el modelo de turbulencia Sparlat-Allmaras, obteniendo diferentes configuraciones de la forma de ondas de choque.
Otros trabajos relevantes para toberas planas con diferentes dimensiones a la tobera plana estudiada por Hunter [10], se mencionan a continuación: Forghany et al. [24] realizaron una investigación computacional 2D de los efectos aerodinámicos en la vectorización de empuje fluídico, obteniendo resultados que el flujo libre disminuye el rendimiento de vectorización y la eficiencia de empuje, en comparación con la condición estática sin viento.
Shimshi et al. [25] indagaron la separación del flujo para un número de Mach alto en la sección divergente, por medios experimentales y simulaciones 2D, y sustentaron que la transición a la separación asimétrica da como resultado la unión del chorro a la pared de la tobera, y la transición inversa va acompañada de un efecto de histéresis. Arora et al. [26] realizaron experimentos para el flujo en una tobera con doble sección divergente, donde observaron que el ángulo que unen las dos divergentes influye en la estructura del choque.
Sivkovik et al. [27] realizaron experimentos y simulaciones 2D del flujo con control de flujo vectorial, con el objetivo de establecer una metodología de la geometría del flujo. Martelli et al. [28] simularon para un flujo asimétrico en 3D, donde reportaron la inestabilidad del choque y las frecuencias de las características. Kostic et al. [29] simularon el flujo en 2D, para el control de vector de empuje con diferentes posiciones, obteniendo el sentido de las desviaciones de la fuerza de empuje y las pérdidas de empuje.
Verma et al. [30] estudiaron la naturaleza inestable de la estructura de choque, de sus resultados señalaron que las fluctuaciones de las presiones en la pared están acompañadas de una resonancia, y a medida que aumenta la relación de presión y la capa límite experimenta una transición los tonos de la resonancia tienden a desaparecer.
En el presente trabajo, se simula el comportamiento del flujo de aire en un dominio computacional 2D de una tobera plana experimental [10], para cinco modelos de turbulencia, con el fin de evaluar y determinar cuál de los resultados numéricos de los modelos de turbulencia empleados tienen mayor cercanía con los datos experimentales de presión estática y de formas de ondas de choque experimentales, para rp = 2, 008 y rp = 3, 413, las cuales están reportados en el trabajo de Hunter [10].
Se presenta el fundamento matemático, se exponen los resultados de las simulaciones y las comparaciones con los datos experimentales; y las comparaciones de las formas de las ondas de choque numéricas con las experimentales. Seguidamente, se exponen las conclusiones del análisis realizado.
2. Materiales y métodos
2.1. Fundamento matemático
Las cuatro ecuaciones gobernantes aplicadas a la dinámica de fluidos para flujo estacionario son: conservación de la masa, (1); cantidad de movimiento, (2); conservación de la energía, (3); y de estado, (4); las cuales se expresan como:
Donde, el tensor de tensiones se expresa como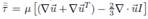 , siendo el tensor unitario I. La energía se expresa como
, siendo el tensor unitario I. La energía se expresa como 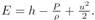 Así como: la densidad ρ, velocidad
Así como: la densidad ρ, velocidad 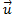 , vector velocidad , presión P, viscosidad μ, entalpía h, constante del gas R, y la temperatura T. Además, en la ecuación de la energía se tiene la conductividad efectiva
, vector velocidad , presión P, viscosidad μ, entalpía h, constante del gas R, y la temperatura T. Además, en la ecuación de la energía se tiene la conductividad efectiva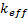 que está en función de la conductividad térmica turbulenta kt, así como el tensor de tensiones efectivo
que está en función de la conductividad térmica turbulenta kt, así como el tensor de tensiones efectivo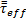 . Para flujo compresible, las relaciones de presiones, Ecuación (5); y de temperaturas, Ecuación (6), en función del número de Mach (M), se establecen como:
. Para flujo compresible, las relaciones de presiones, Ecuación (5); y de temperaturas, Ecuación (6), en función del número de Mach (M), se establecen como:
Donde, los parámetros son: presión total P0, la temperatura total T0. El número de Mach M =  . La velocidad del sonido se expresa como c =
. La velocidad del sonido se expresa como c = 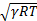 ; siendo la constante del gas R, relación de calor específico c =
; siendo la constante del gas R, relación de calor específico c = 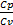 . Las consideraciones del número de Mach son las siguientes: para flujo incompresible M < 0, 3, flujo subsónico 0, 3 < M < 0, 8, flujo transónico 0, 8 < M < 1, 2, flujo supersónico 1, 2 < M < 3, flujo hipersónico M > 3. Y, para el flujo con velocidad sónica, se tiene M = 1 [5].
. Las consideraciones del número de Mach son las siguientes: para flujo incompresible M < 0, 3, flujo subsónico 0, 3 < M < 0, 8, flujo transónico 0, 8 < M < 1, 2, flujo supersónico 1, 2 < M < 3, flujo hipersónico M > 3. Y, para el flujo con velocidad sónica, se tiene M = 1 [5].
La variación de la viscosidad para gases en función de la temperatura, Ecuación (7); se expresa como un aproximado de acuerdo con la ley de Sutherland [5].
Donde, la viscosidad de referencia μ0 = 1, 716 kg/(m.s), la temperatura de referencia T0 = 273, 11 K, y la temperatura efectiva S = 110, 56 K.
Existen diferentes modelos de turbulencia reportados en la literatura y están fundamentados sus modelos matemáticos. Los modelos de turbulencia son ecuaciones de transporte semiempíricas que modelan el mezclado y difusión que se incrementan a causa de remolinos turbulentos, en función de la viscosidad del fluido y de la viscosidad turbulenta, entre otras variables. Los modelos de turbulencia están acoplados en la ecuación de la cantidad de movimiento lineal, y el tensor de tensiones está en función de la viscosidad. Esta expresión matemática es la ecuación de Navier-Stokes de número de Reynolds promedio (NSRP, RANS por sus siglas en inglés). Además de NSRP, se tiene el modelo de simulación de remolinos grandes (SRG, LES por sus siglas en inglés) y el modelo de simulación numérica directa (SND, DNS por sus siglas en inglés). Las primeras investigaciones de la turbulencia fueron desarrolladas por Kolmogorov (1941) basándose en los resultados de Reynolds (1883).
Los cinco modelos de turbulencia empleados en las simulaciones numéricas, mediante RANS, son las siguientes: SST k −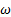 de Menter [20], k−e estándar de Launder y Spalding [16], k −
de Menter [20], k−e estándar de Launder y Spalding [16], k − 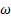 estándar de Wilcox [31], k − kl −
estándar de Wilcox [31], k − kl − 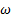 de transición de Walters y Cokljat [32], los cuales están basados en la viscosidad turbulenta y están sustentados por la hipótesis de Boussinesq. El modelo de turbulencia RSM de Launder et al. [21] para la tensión lineal de presión [33] y efectos de reflexión de la pared [34] está sustentando en los modelos de tensiones de Reynolds.
de transición de Walters y Cokljat [32], los cuales están basados en la viscosidad turbulenta y están sustentados por la hipótesis de Boussinesq. El modelo de turbulencia RSM de Launder et al. [21] para la tensión lineal de presión [33] y efectos de reflexión de la pared [34] está sustentando en los modelos de tensiones de Reynolds.
2.2. Dominio computacional, mallado y condiciones de borde
La geometría de la tobera plana [10] estudiada en el presente trabajo se muestra en la Figura 2, y las dimensiones de los puntos de referencias se observan en la Tabla 1.
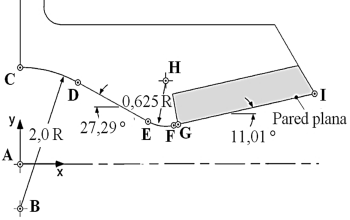
Figura 2. Esquema de la tobera plana proyectada en el plano cartesiano xy. Adaptada del trabajo de Hunter [10].
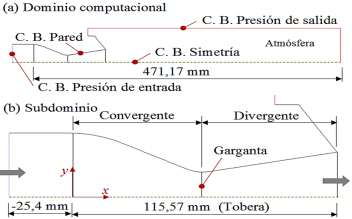
La geometría del dominio computacional 2D se observa en la Figura 3, la cual está proyectada en el plano cartesiano xy, siendo consideradas las paredes del dominio paredes adiabáticas. Se simula el flujo para esta sección por la simetría que tiene. La geometría de la tobera se construye con las dimensiones presentadas en la Tabla 1.
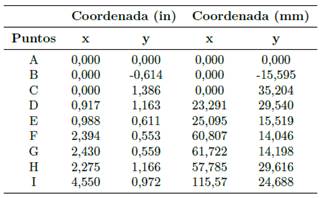
Tabla 1. Dimensiones en pulgadas y en milímetros de puntos de referencias de la tobera plana. Adaptado del trabajo de Hunter [10]
Antes de la sección convergente, hay un tramo recto de longitud x = −25, 4 mm; la tobera inicia en x = 0, 0 mm, la garganta se ubica en x = 57, 785 mm, y la sección divergente de la tobera termina en x = 115, 57 mm; la longitud de la sección de la atmósfera termina en x = 471, 17 mm.
La Figura 4 muestra el dominio mallado, siendo la malla estructurada con celdas cuadriláteras, para un total de 20 290 celdas. La malla se refinó hacia las paredes de la sección recta y de la sección convergentedivergente, por la presencia del esfuerzo cortante en esas regiones.
El mallado se realizó en la plataforma ANSYSMeshing y se discretizó el dominio mediante la interacción de ICEM-CFD. Siendo para el dimensionamiento: suavizado, medio; centro de ángulo de expansión, fino; curvatura de ángulo normal, 18°; tamaño mínimo, 0,000249 m; tamaño máximo de superficie, 0,0249 m; máximo tamaño, 0,0499 m; relación de crecimiento, 1,2; y longitud mínima del borde, 0,000914 m. Para la inflación: relación de transición, 0,272; capas máximas, 2; y relación de crecimiento, 1,2.
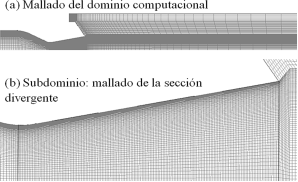
Figura 4. (a) Dominio computacional mallado con 20 290 celdas cuadriláteras. (b) Mallado de la sección divergente con 11 270 celdas cuadriláteras.
Cabe señalar que, para obtener una buena calidad de la malla, se debe tomar en cuenta que cada una de las celdas no esté muy sesgada porque esto puede crear dificultades e inexactitudes en la convergencia de las soluciones numéricas. El tipo de sesgo más apropiado para celdas bidimensionales es el sesgo equiángulo QEAS, donde 0 ≤ QEAS ≤ 1 para cualquier celda 2D, donde un triángulo equilátero y un cuadrado o rectángulo tiene sesgo cero [35]. Para la malla con celdas cuadriláteras del dominio mostrado en la Figura 4, se tiene QEAS = 0 para un 98% del total de las celdas y QEAS = 0, 3 para un 2 % de las celdas restantes, siendo la malla del dominio computacional de buena calidad.
Como parte de un estudio de convergencia numérica, la malla mostrada en la Figura 4, presentó un resultado satisfactorio, al evaluar el número de Mach al final de la sección divergente en la simetría axial, en la distancia 115,57 mm, para rp = 8, 78, y empleando el modelo de turbulencia SST k − 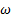 , donde se obtuvo el valor de Mach 2,0036 como resultado final, lo cual es un valor aceptable al comparar con el valor de Mach 2,07 de diseño en la salida de la tobera plana del trabajo de Hunter [10].
, donde se obtuvo el valor de Mach 2,0036 como resultado final, lo cual es un valor aceptable al comparar con el valor de Mach 2,07 de diseño en la salida de la tobera plana del trabajo de Hunter [10].
Las condiciones iniciales y de borde se establecen como:
· En la atmósfera, la presión de salida es la presión total Patm = 102, 387kPa (14,85 psi), la temperatura total Tatm = 294, 444K (530 °R).
· La presión total de entrada del flujo se establece para dos casos de relaciones de presiones rp = 2, 008 y rp = 3, 413. Siendo la presión total de entrada P0 = rp · Patm.
· La temperatura total de entrada T0 = 294, 444K (530° R), siendo de igual magnitud que la temperatura de la atmósfera. Por la simetría del dominio en el eje x, en dirección del eje y la velocidad del flujo es nula.
La velocidad del flujo es nula en las paredes adiabáticas.
Donde, los datos de presión y de temperatura, para rp = 2, 008 y rp = 3, 413, han sido tomados del trabajo de Hunter [10].
2.3. Método de solución computacional y equipo
Para las simulaciones numéricas del flujo de aire, se empleó el código ANSYS-Fluent versión 12.1, el cual aplica el método de volumen finito (MVF). Dentro de las diferentes alternativas de solución, se seleccionó la opción de análisis basado en densidad para un fluido compresible, y simetría en 2D en el plano cartesiano xy.
En cada simulación numérica se seleccionó un solo modelo de turbulencia, en el siguiente orden: SST k − 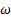 , k − e estándar, k −
, k − e estándar, k − 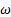 estándar, k − kl −
estándar, k − kl − 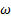 de transición y RSM, siendo en total cinco modelos. Para la viscosidad del fluido en función de la temperatura se seleccionó la ecuación de Sutherland. En las condiciones del flujo, para la turbulencia de la energía cinética y para el tipo de disipación específica, se seleccionó la opción: Second Order Upwin. Para la solución de control, se determinó el número de Courant igual a 2, manteniendo por defecto los factores de relajación. Para el monitor residual se determinó un valor fijo de 0,00001, tanto para continuidad, velocidad y energía. Se realizaron 9000-14 000 iteraciones para obtener los resultados finales, para las condiciones del flujo en estado estacionario.
de transición y RSM, siendo en total cinco modelos. Para la viscosidad del fluido en función de la temperatura se seleccionó la ecuación de Sutherland. En las condiciones del flujo, para la turbulencia de la energía cinética y para el tipo de disipación específica, se seleccionó la opción: Second Order Upwin. Para la solución de control, se determinó el número de Courant igual a 2, manteniendo por defecto los factores de relajación. Para el monitor residual se determinó un valor fijo de 0,00001, tanto para continuidad, velocidad y energía. Se realizaron 9000-14 000 iteraciones para obtener los resultados finales, para las condiciones del flujo en estado estacionario.
Para el procesamiento de datos de las simulaciones numéricas, se empleó un equipo con las siguientes características: Laptop marca Síragon, modelo M54R, Intel Core 2 Duo, dos procesadores de 1,8 GHz y memoria RAM de 3 GB.
3. Resultados y discusión
3.1. Comparación de perfiles de presiones estáticas con datos experimentales
En esta sección, las curvas numéricas de presión estática obtenidas para cinco modelos de turbulencia: SST k −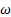 , k−e estándar, k −
, k−e estándar, k − 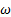 estándar, k −kl −
estándar, k −kl −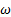 De transición y RSM, se comparan con datos experimentales de presión estática del trabajo de Hunter [10], para rp = 2, 008 y rp = 3, 413, respectivamente. Donde, los perfiles de presión estática corresponden a las presiones a lo largo de la pared de la tobera, iniciando en la entrada de la sección convergente y finalizando en la salida de la sección divergente.
De transición y RSM, se comparan con datos experimentales de presión estática del trabajo de Hunter [10], para rp = 2, 008 y rp = 3, 413, respectivamente. Donde, los perfiles de presión estática corresponden a las presiones a lo largo de la pared de la tobera, iniciando en la entrada de la sección convergente y finalizando en la salida de la sección divergente.
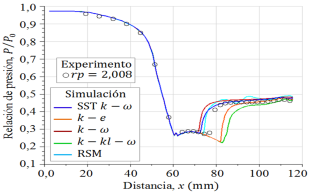
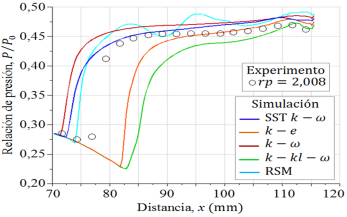
En la Figura 5 se ven los perfiles de presión estática, para rp = 2, 008. Donde, durante la caída y después de un incremento ligero de la presión estática, las cinco curvas numéricas tienen cercanía y están superpuestos con los datos experimentales hasta una posición estimada x = 70mm, después de esta distancia se separan las curvas numéricas uno con respecto a otro, y luego se acercan camino a la salida de la sección divergente.
En el detalle ampliado, la cual se ilustra en la Figura 6, se observa cómo evolucionan las trayectorias de las curvas numéricas después de la posición de x = 70mm. Donde se produce el inicio del incremento de la presión estática, allí se inicia la separación del flujo de la pared. La curva numérica SST k − 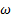 tiene mayor acercamiento con los datos experimentales. La curva numérica RSM tiene un comportamiento oscilatorio sobre los datos experimentales de presión. La curva numérica k −
tiene mayor acercamiento con los datos experimentales. La curva numérica RSM tiene un comportamiento oscilatorio sobre los datos experimentales de presión. La curva numérica k − 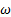 estándar tiene un comportamiento paralelo a la curva SST k −
estándar tiene un comportamiento paralelo a la curva SST k − 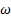 por la parte superior. Y, las curvas numéricas k − e estándar y k − kl −
por la parte superior. Y, las curvas numéricas k − e estándar y k − kl − 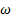 de transición están muy alejados de los datos experimentales por la parte inferior donde se produce la caída mínima de presión.
de transición están muy alejados de los datos experimentales por la parte inferior donde se produce la caída mínima de presión.
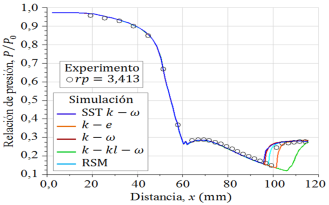
Los perfiles de presión estática para rp = 3, 413, se presentan en la Figura 7, las cuales tienen cercanía con los datos experimentales hasta la posición estimada x = 95mm, luego de esta posición, se separan.
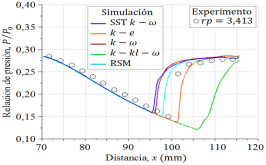
En el detalle ampliado, la cual se muestra en la Figura 8, se observa cómo evolucionan las trayectorias a partir de la posición x = 70mm. Luego de x = 95mm, el modelo turbulencia k −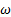 estándar y SST k −
estándar y SST k − 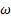 están superpuestos, con una pequeña diferencia de separación en la dirección vertical y cercano a los datos experimentales, sin embargo, con respecto a estas dos curvas numéricas, la curva numérica RSM está más cercana a los datos experimentales por la parte superior con pequeñas oscilaciones, y la curva numérica k − e estándar por la parte inferior, y la que está más alejada de los datos experimentales es la curva numérica k − kl −
están superpuestos, con una pequeña diferencia de separación en la dirección vertical y cercano a los datos experimentales, sin embargo, con respecto a estas dos curvas numéricas, la curva numérica RSM está más cercana a los datos experimentales por la parte superior con pequeñas oscilaciones, y la curva numérica k − e estándar por la parte inferior, y la que está más alejada de los datos experimentales es la curva numérica k − kl − 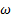 de transición.
de transición.
De la comparación de las curvas numéricas que se observan las Figuras 5 y 7, con respecto a los datos experimentales de presión estática de la tobera plana del trabajo de Hunter [10], el modelo de turbulencia SST k − 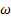 de Menter [20] tiene mayor aproximación con los datos experimentales de presiones estáticas.
de Menter [20] tiene mayor aproximación con los datos experimentales de presiones estáticas.
3.2. Comparación de formas de ondas de choque numéricas con experimentales
Las simulaciones numéricas del campo de flujo con presencia de ondas de choque en la tobera plana, obtenidos para los cinco modelos de turbulencia, se dan en las Figuras 9 y 10 para rp = 2, 008, y en las Figuras 11 y 12 para rp = 3, 413, respectivamente
Para el flujo de aire con rp = 2, 008, en la sección divergente el flujo está sobreexpandido, por tanto, está presente la onda de choque y se observa en qué regiones se muestra el disco de Mach, el choque oblicuo, el choque oblicuo reflejado y el inicio de la separación del flujo, habiendo regiones donde el flujo es supersónico, transónico y subsónico.
El flujo sobreexpandido es característico cuando el flujo se desacelera en la sección divergente por el incremento abrupto de la presión, pasando de una velocidad supersónica a una velocidad subsónica cuando se produce el choque. A medida que la presión del flujo a la entrada de la tobera se incrementa, la onda de choque se mueve hacia la salida de la tobera.
Así mismo, se muestran para el flujo de aire con rp = 3, 413, siendo también el flujo sobreexpandido en la sección divergente, donde se presenta el disco de Mach y el choque oblicuo reflejado fuera de la tobera.
Donde, la sección divergente está en el rango de x/xt = 1, 0 − 2, 0, donde xt es la distancia variable desde la posición de la garganta hasta la salida de la tobera, en el rango de 57, 785 − 115, 57 mm.
Para cada caso, a partir del inicio de la separación del flujo, aguas abajo para el flujo adyacente a la pared de la tobera, producto de la caída de presión, se produce una recirculación del flujo, por tanto, una cantidad de masa de aire proveniente de la atmósfera es forzada a ingresar rozando la pared de la tobera.
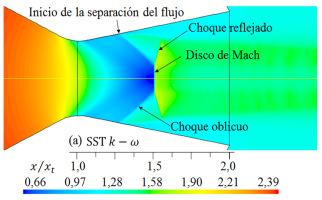
Figura 9. Formas de ondas de choque para diferentes modelos de turbulencia. Densidad (kg/m3) del flujo para rp = 3, 413.
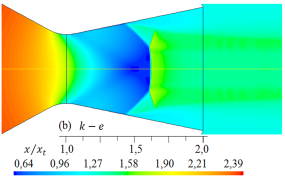
Figura 9. Formas de ondas de choque para diferentes modelos de turbulencia. Densidad (kg/m3) del flujo para rp = 3, 413.
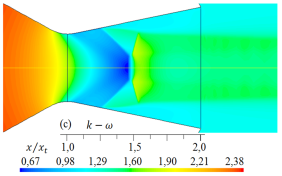
Figura 9. Formas de ondas de choque para diferentes modelos de turbulencia. Densidad (kg/m3) del flujo para rp = 3, 413.
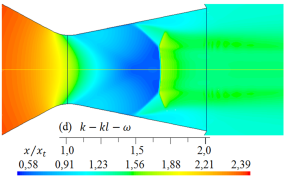
Figura 9. Formas de ondas de choque para diferentes modelos de turbulencia. Densidad (kg/m3) del flujo para rp = 3, 413..
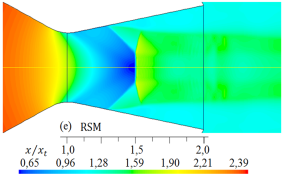
Figura 9. Formas de ondas de choque para diferentes modelos de turbulencia. Densidad (kg/m3) del flujo para rp = 3, 413.
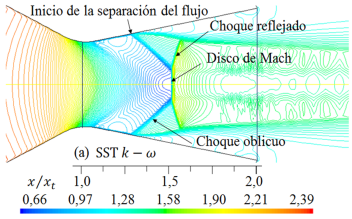
Figura 10. Formas de ondas de choque para diferentes modelos de turbulencia. Líneas de contorno de densidad (kg/m3) para rp = 3, 413.
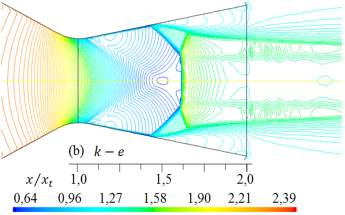
Figura 10. Formas de ondas de choque para diferentes modelos de turbulencia. Líneas de contorno de densidad (kg/m3) para rp = 3, 413.
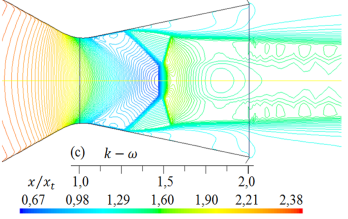
Figura 10 Formas de ondas de choque para diferentes modelos de turbulencia. Líneas de contorno de densidad (kg/m3) para rp = 3, 413.
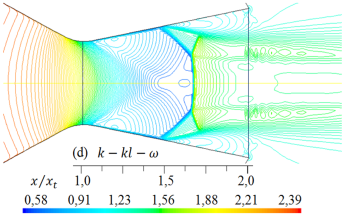
Figura 10. Formas de ondas de choque para diferentes modelos de turbulencia. Líneas de contorno de densidad (kg/m3) para rp = 3, 413.
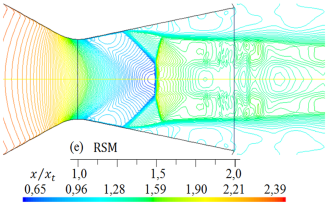
Figura 10. Formas de ondas de choque para diferentes modelos de turbulencia. Líneas de contorno de densidad (kg/m3) para rp = 3, 413.
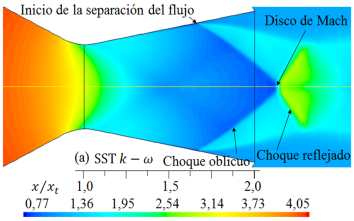
Figura 11. Formas de ondas de choque para diferentes modelos de turbulencia. Densidad (kg/m3) del flujo para rp = 3, 413.
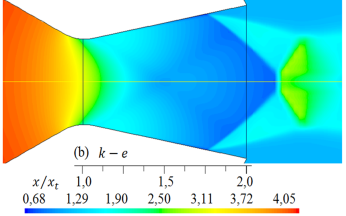
Figura 11. Formas de ondas de choque para diferentes modelos de turbulencia. Densidad (kg/m3) del flujo para rp = 3, 413.
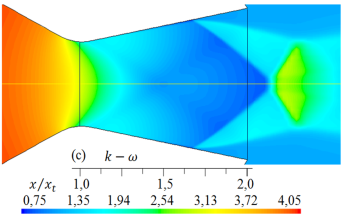
Figura 11. Formas de ondas de choque para diferentes modelos de turbulencia. Densidad (kg/m3) del flujo para rp = 3, 413.
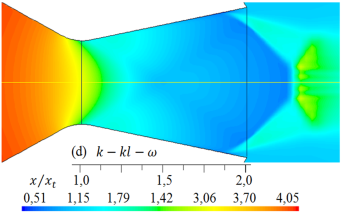
Figura 11. Formas de ondas de choque para diferentes modelos de turbulencia. Densidad (kg/m3) del flujo para rp = 3, 413.
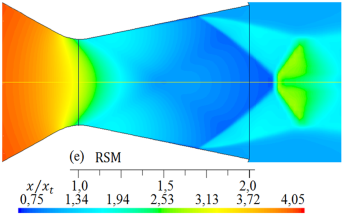
Figura 11. Formas de ondas de choque para diferentes modelos de turbulencia. Densidad (kg/m3) del flujo para rp = 3, 413.
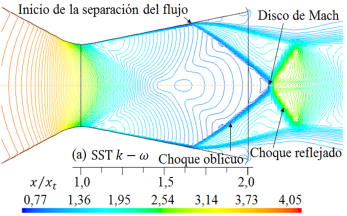
Figura 12. Formas de ondas de choque para diferentes modelos de turbulencia. Líneas de contorno de densidad (kg/m3) para rp = 3, 413.
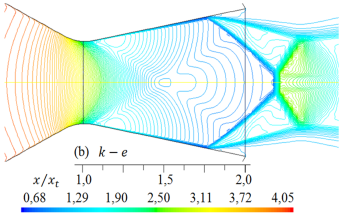
Figura 12. Formas de ondas de choque para diferentes modelos de turbulencia. Líneas de contorno de densidad (kg/m3) para rp = 3, 413.
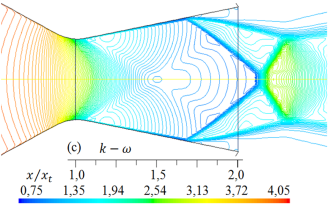
Figura 12. Formas de ondas de choque para diferentes modelos de turbulencia. Líneas de contorno de densidad (kg/m3) para rp = 3, 413.
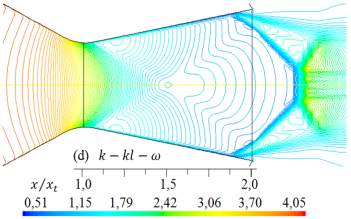
Figura 12. Formas de ondas de choque para diferentes modelos de turbulencia. Líneas de contorno de densidad (kg/m3) para rp = 3, 413.
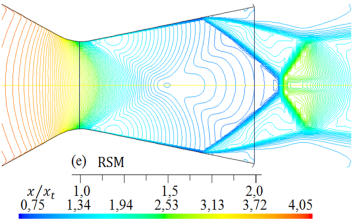
Figura 12. Formas de ondas de choque para diferentes modelos de turbulencia. Líneas de contorno de densidad (kg/m3) para rp = 3, 413.
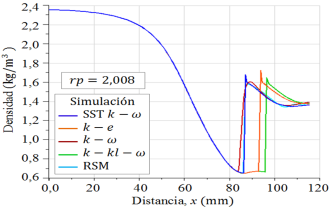
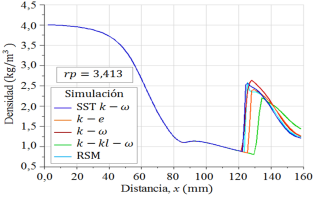
Los perfiles de las densidades del flujo obtenidas a lo largo de la simetría en dirección del eje x, para los cinco modelos de turbulencia, se muestran en la Figura 13 para rp = 2, 008, y en la Figura 14 para rp = 3, 413. Donde, para cada caso, se expone el comportamiento de las trayectorias de las curvas numéricas, la disminución e incremento de la densidad donde se presenta la onda de choque.
Al comparar los resultados numéricos de las formas de las ondas de choque de la Figura 9 y 10 para rp = 2, 008, con la forma de la onda de choque experimental captada con la técnica Schlieren que se observa en la Figura 15, la cual ha sido tomada del trabajo de Hunter [10], se muestra que para el modelo de turbulencia SST k − 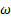 , el disco de Mach en la posición x/xt = 1, 5, así como, el choque oblicuo, el choque reflejado y el inicio de la separación del flujo, son semejantes con el resultado experimental. Los otros resultados numéricos de las formas de las ondas de choque se desplazan a la izquierda y otros a la derecha, por tanto, moviéndose el disco de Mach para la posición x/xt = 1, 5. Cabe señalar, las anchuras de los discos de Mach, la cual es un frente de onda normal, varían su anchura para cada modelo de turbulencia.
, el disco de Mach en la posición x/xt = 1, 5, así como, el choque oblicuo, el choque reflejado y el inicio de la separación del flujo, son semejantes con el resultado experimental. Los otros resultados numéricos de las formas de las ondas de choque se desplazan a la izquierda y otros a la derecha, por tanto, moviéndose el disco de Mach para la posición x/xt = 1, 5. Cabe señalar, las anchuras de los discos de Mach, la cual es un frente de onda normal, varían su anchura para cada modelo de turbulencia.
De igual modo, al comparar las formas de las ondas de choque que se muestran en las Figuras 11 y 12, para rp = 3, 413, con la forma de la onda de choque experimental en la Figura 16 la forma de la onda de choque obtenido con el modelo de turbulencia SST k − 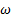 , se ajusta más al resultado experimental, pero, el disco de Mach, que está fuera de la tobera, es de menor longitud con respecto a la forma de onda de choque experimental. Las otras formas de ondas de choque numéricas, se desplazan a la izquierda y otros a la derecha, por lo tanto, también lo hará el disco de Mach.
, se ajusta más al resultado experimental, pero, el disco de Mach, que está fuera de la tobera, es de menor longitud con respecto a la forma de onda de choque experimental. Las otras formas de ondas de choque numéricas, se desplazan a la izquierda y otros a la derecha, por lo tanto, también lo hará el disco de Mach.
Como se muestra en las Figuras del 9 al 12, las formas de las ondas de choque varían su forma de acuerdo con cada modelo de turbulencia empleado en las simulaciones, y el inicio de la separación del flujo no se mantiene en una posición fija.
El disco de Mach experimental para rp = 2, 008 se encuentra en x/xt = 1, 5, siendo la ubicación en x = 86, 677 mm, donde xt = 57, 785 mm. Por la diferencia de densidad, la cual se puede apreciar por la escala de color gris, se observa que existe un espesor de la onda de choque, pues, el flujo pasa de una baja presión a una alta presión de forma repentina, así como la velocidad del flujo se desacelera repentinamente en un instante de tiempo. Lo mismo sucede para la onda de choque que se presenta fuera de la tobera para rp = 3, 413 en x/xt = 2, 11, siendo la posición x = 122, 06 mm.
De las simulaciones numéricas, se ha obtenido los espesores del frente de onda para el disco de Mach en la simetría del eje x del dominio del flujo compresible, la posición para cada disco de Mach y el porcentaje de desplazamiento de los mismos, los cuales se muestran en la Tabla 2 para rp = 2, 008 y en la Tabla 3 para 3, 413
El flujo simulado para rp = 2, 008, la posición de los discos de Mach son coincidentes para SST k −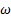 y k −
y k − 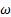 estándar y están alejados 0, 0068 % por el extremo izquierdo de la posición del disco de Mach experimental, donde en la Tabla 2 se muestra el signo negativo lo cual indica que el disco se desplaza a la izquierda. Mientras que, por el extremo derecho están alejados k − e estándar con un 7, 86 %, k − kl −
estándar y están alejados 0, 0068 % por el extremo izquierdo de la posición del disco de Mach experimental, donde en la Tabla 2 se muestra el signo negativo lo cual indica que el disco se desplaza a la izquierda. Mientras que, por el extremo derecho están alejados k − e estándar con un 7, 86 %, k − kl − 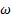 de transición con 10, 96 % y RSM con 0, 61 %. El que tiene mayor espesor del disco de Mach es k −
de transición con 10, 96 % y RSM con 0, 61 %. El que tiene mayor espesor del disco de Mach es k − 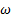 estándar y el menor k − kl −
estándar y el menor k − kl − 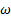 de transición. Los discos de Mach para los modelos de turbulencia SST k −
de transición. Los discos de Mach para los modelos de turbulencia SST k − 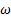 , k −
, k − 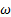 estándar y RSM tienen menos del 1 % de desplazamiento con respecto a la posición del disco de Mach experimental, lo cual es aceptable en términos de ingeniería, sin embargo, de acuerdo con los resultados numéricos, el que se ajusta más al experimento es el modelo de turbulencia SST k −
estándar y RSM tienen menos del 1 % de desplazamiento con respecto a la posición del disco de Mach experimental, lo cual es aceptable en términos de ingeniería, sin embargo, de acuerdo con los resultados numéricos, el que se ajusta más al experimento es el modelo de turbulencia SST k −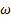 .
.
Cabe señalar, el espesor del disco de Mach fue obtenido de los perfiles de densidad, en la simetría del eje x, desde la posición inicial donde el flujo inicia a incrementar su densidad hasta la posición final donde alcanza la máxima compresión, el incremento de la densidad se muestra en la Figura 13, para el rango estimado de 85-90 mm, y es en esa región donde se presenta el frente de choque para las simulaciones numéricas.
Para rp = 3, 413, todas las posiciones de los discos de Mach están desplazados hacia la derecha con respecto al disco de Mach experimental, tal como se muestran en la Tabla 3. El que tiene menor porcentaje de desplazamiento es SST k − 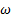 con 1, 27 % y el que tiene mayor es k − kl −
con 1, 27 % y el que tiene mayor es k − kl − 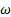 de transición con 8, 14 %. Para este caso, todos los espesores del disco de Mach son mayores con respecto al flujo simulado para rp = 2, 008. Al igual que en el caso anterior, el resultado del modelo de turbulencia SST k −
de transición con 8, 14 %. Para este caso, todos los espesores del disco de Mach son mayores con respecto al flujo simulado para rp = 2, 008. Al igual que en el caso anterior, el resultado del modelo de turbulencia SST k − 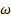 se ajusta más al experimento.
se ajusta más al experimento.
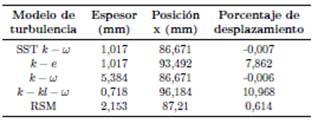
Tabla 2. Espesores del disco de Mach, posiciones y porcentajes de desplazamiento del disco con respecto al disco de Mach experimental en x = 86, 677 mm, para rp = 2, 008
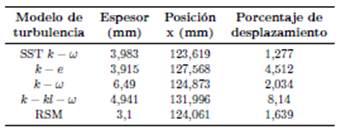
Tabla 3. Espesores del disco de Mach, posiciones y porcentajes de desplazamiento del disco con respecto al disco de Mach experimental en x = 122, 06 mm, para rp = 3, 413
Para ambos casos, rp = 2, 008 y rp = 3, 413, el flujo que está sobreexpandido en la sección divergente de la tobera plana, las formas de las ondas de choque obtenidas con el modelo de turbulencia SST k − 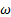 se ajustan más a las ondas de choque experimentales que se muestran en las Figuras 15 y 16.
se ajustan más a las ondas de choque experimentales que se muestran en las Figuras 15 y 16.
Cabe señalar, un caso de estudio para la misma geometría de la tobera plana [10] estudiada en el presente trabajo, pero adaptada con una superficie porosa en la pared plana en la sección divergente fue realizado por Abdol-Hamid et al. [36], quienes simularon el flujo en 3D para tres modelos de turbulencia k – e estándar [16], SZL [12] y RSM [21], comparando con resultados experimentales, y los resultados tridimensionales obtenidos en la simetría de la pared plana, no contribuyeron significativamente en una mejora cuando fueron comparados con resultados en 2D, para el rango de la relación de presión de 1, 41 < rp < 2, 1.
Para el flujo en dominios que tienen simetría, la opción favorable es simular en 2D por el ahorro de horas de costo computacional, el cual reduce el tiempo de iteración, obteniendo resultados favorables en regiones específicas, sin tener que recurrir a la simulación del flujo en 3D para obtener resultados similares en la simetría. Sin embargo, la simulación 3D aporta información relevante lejos de la simetría, en las esquinas de las paredes, donde el régimen del flujo sufre cambios repentinos, y para esto, se debe de tener en cuenta cuales son los modelos de turbulencia que han sido validados para emplearlos, y más aún, si se quiere mayor precisión en los resultados numéricos, se debe emplear el modelo LES o el modelo DNS.
Estos resultados numéricos obtenidos tienen que ver con los fundamentos matemáticos de cada modelo de turbulencia y el método de evaluación que aplican en la región de la capa límite turbulento, ya que, en esa región del flujo, están presente el esfuerzo cortante. Además, existen dos parámetros involucrados, el espesor y el coeficiente de fricción, en la capa límite, tanto para flujo laminar o turbulento.
El modelo de turbulencia SST k − 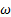 es un modelo de transporte de esfuerzo cortante (SST, Shear Stress Transport) que emplea dos ecuaciones, una para la energía cinética turbulenta k, y la otra para la tasa específica de disipación
es un modelo de transporte de esfuerzo cortante (SST, Shear Stress Transport) que emplea dos ecuaciones, una para la energía cinética turbulenta k, y la otra para la tasa específica de disipación 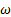 , y este último determina la escala de la turbulencia. Las expresiones matemáticas que son parte de la estructura son: la viscosidad de remolino, el cual, es el transporte de la cantidad de movimiento mediante remolinos turbulentos; la generación de energía cinética turbulenta debido a los gradientes de velocidad media, la difusión transversal, entre otras variables, y constantes que son empleados como parámetros para el desarrollo del régimen del flujo. Este modelo tiene la virtud de predecir con mayor precisión el comportamiento del flujo compresible para gradientes de presión adverso, lo cual se demuestra en las simulaciones donde se produce el frente de onda de choque en la simetría en dirección del eje x. La sensibilidad de las variaciones de presión por el incremento brusco, donde se produce la separación del flujo de la pared divergente, es ligeramente menor con respecto a los modelos de turbulencia k − e y RSM, los cuales están más cercanos a los datos experimentales, sin embargo, el modelo de turbulencia SST k −
, y este último determina la escala de la turbulencia. Las expresiones matemáticas que son parte de la estructura son: la viscosidad de remolino, el cual, es el transporte de la cantidad de movimiento mediante remolinos turbulentos; la generación de energía cinética turbulenta debido a los gradientes de velocidad media, la difusión transversal, entre otras variables, y constantes que son empleados como parámetros para el desarrollo del régimen del flujo. Este modelo tiene la virtud de predecir con mayor precisión el comportamiento del flujo compresible para gradientes de presión adverso, lo cual se demuestra en las simulaciones donde se produce el frente de onda de choque en la simetría en dirección del eje x. La sensibilidad de las variaciones de presión por el incremento brusco, donde se produce la separación del flujo de la pared divergente, es ligeramente menor con respecto a los modelos de turbulencia k − e y RSM, los cuales están más cercanos a los datos experimentales, sin embargo, el modelo de turbulencia SST k −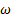 presenta mejores resultados numéricos con respecto a los otros modelos de turbulencias empleados.
presenta mejores resultados numéricos con respecto a los otros modelos de turbulencias empleados.
4. Conclusiones
Sobre la base de las evaluaciones de los cinco modelos de turbulencia SST k −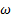 , k −
, k − 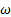 estándar, k – e estándar, k − kl −
estándar, k – e estándar, k − kl − 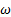 de transición y RSM, las cuales fueron empleados en las simulaciones numéricas, para un flujo que está sobreexpandido, se concluye que:
de transición y RSM, las cuales fueron empleados en las simulaciones numéricas, para un flujo que está sobreexpandido, se concluye que:
Los perfiles de presión estática obtenidos en las simulaciones a lo largo de las paredes de la tobera plana, con el modelo de turbulencia SST k − 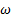 , para las relaciones de presión rp = 2, 008 y rp = 3, 413, se ajustan más a los datos experimentales.
, para las relaciones de presión rp = 2, 008 y rp = 3, 413, se ajustan más a los datos experimentales.
Los perfiles de densidad evaluados en la simetría del eje x, para rp = 2, 008 y rp = 3, 413, muestran el incremento brusco de la magnitud de la densidad donde se presenta la onda de choque, y el que tiene la pendiente más pronunciada es el modelo de turbulencia SST k −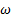
Las formas de las ondas de choque para el campo de densidad, obtenidas en las simulaciones con el modelo de turbulencia SST k −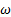 , para las relaciones de presión rp = 2, 008 y rp = 3, 413, son semejantes a las formas de ondas de choque experimentales captadas con la técnica Schlieren, donde para rp = 2, 008 la posición del disco de Mach está desplazada hacia la izquierda 0,007 % y para rp = 3, 413 el disco de Mach está desplazado hacia la derecha 1,277 %.
, para las relaciones de presión rp = 2, 008 y rp = 3, 413, son semejantes a las formas de ondas de choque experimentales captadas con la técnica Schlieren, donde para rp = 2, 008 la posición del disco de Mach está desplazada hacia la izquierda 0,007 % y para rp = 3, 413 el disco de Mach está desplazado hacia la derecha 1,277 %.
Para trabajos posteriores, se recomienda simular el flujo en 3D y comparar con los resultados del presente trabajo, para determinar las desviaciones numéricas que pudieran ocurrir al comparar con los datos experimentales de presión. Además, con el modelo de turbulencia SST k − 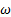 simular el flujo para el campo de temperatura estática, el campo de número de Mach y el campo de presión, para obtener las magnitudes de los parámetros físicos antes y después de la onda de choque.
simular el flujo para el campo de temperatura estática, el campo de número de Mach y el campo de presión, para obtener las magnitudes de los parámetros físicos antes y después de la onda de choque.
Agradecimientos
Mi agradecimiento a Jehová, mi Dios todopoderoso, mi fuente de sabiduría e inspiración. Al Departamento de Ingeniería Mecánica de la Universidad Nacional Experimental Politécnica “AJS” Vice-Rectorado Puerto Ordaz (UNEXPO), Bolívar, Venezuela. Al Grupo de Modelamiento Matemático y Simulación Numérica (GMMNS, Group of Mathematical Modeling and Numerical Simulation) de la Universidad Nacional de Ingeniería (UNI), Lima, Perú.