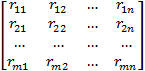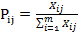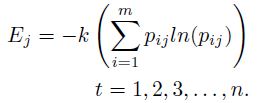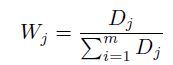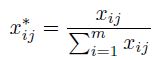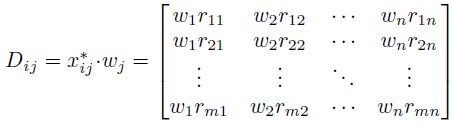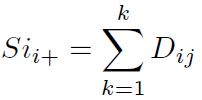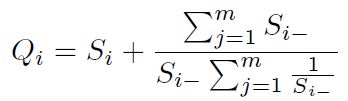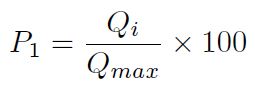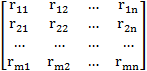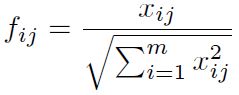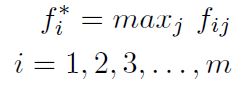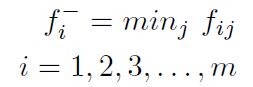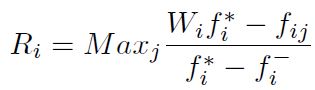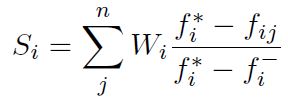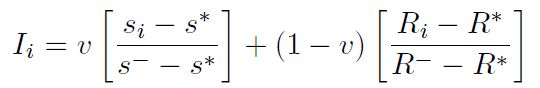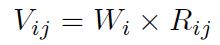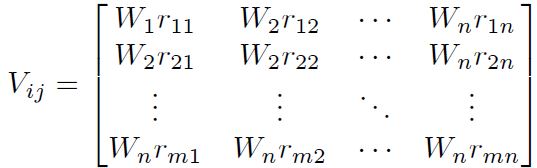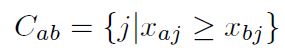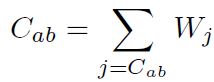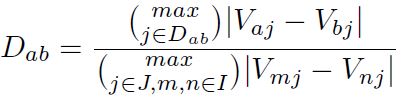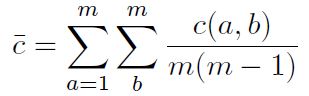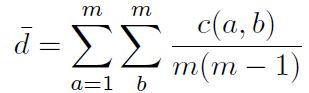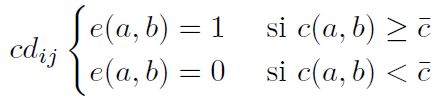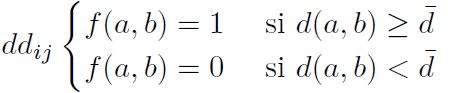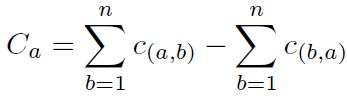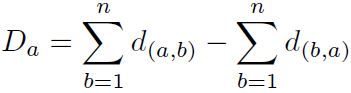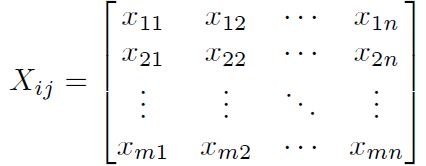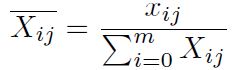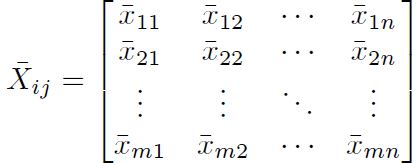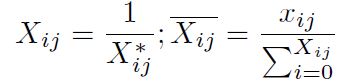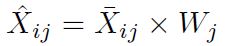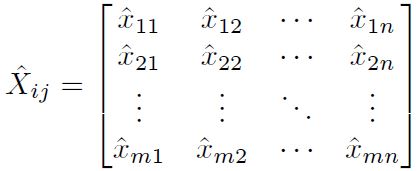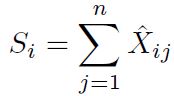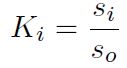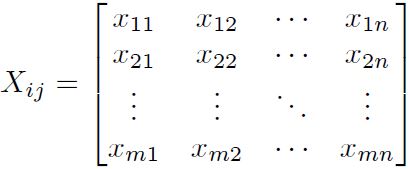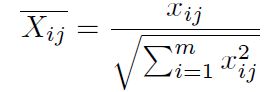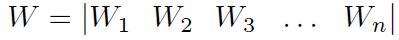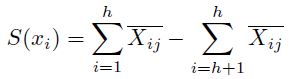Introducción
En el desarrollo de la industria automotriz, los frenos constituyen uno de los principales dispositivos de seguridad, por lo tanto, los materiales a seleccionar deben poseer las propiedades físicas y mecánicas adecuadas para un óptimo rendimiento del disco de freno.
La formación de grietas térmicas en los materiales empleados en disco de frenos depende de la fatiga térmica o esfuerzos térmicos muy severos, producidos por la variación de temperatura durante el frenado y condiciones ambientales de operación [1]. En el frenado las energías cinética y potencial se convierten en energía térmica, por lo tanto, es necesario conocer la temperatura y tensión térmica en el frenado [2]. Es necesario investigar sobre el uso de nuevos materiales que mejoren la eficiencia de frenado y proporcionen mayor estabilidad y seguridad al vehículo [3]. Es importante seleccionar un material alternativo al hierro fundido por un material ligero para reducir el consumo de combustible, en función de su peso específico [4].
El método proceso analítico jerárquico (AHP del inglés Analytic Hierarchy Process) se utiliza para la evaluación ambiental en la selección de materiales compuestos para componentes automotrices, porque los datos disponibles son difíciles de cuantificar y las características a evaluar son intangibles de un modelo analítico [5]. Es necesario un enfoque sistemático y eficiente hacia la selección de materiales a fin de seleccionar la mejor alternativa para una aplicación determinada de ingeniería [6]. Los métodos multicriterios como el COPRAS (Complex Proportional. Assessment), VIKOR (del serbio: VIseKriterijumska Optimizacija I Kompromisno Resenje: Multicriteria Optimization and Compromise Solution), ELECTRE I (Elimination and Choice Expressing the Reality), ARAS (additive ratio assessment), MOORA (multi-objective optimization on the basis of ratio analysis) y el de ENTROPÍA que se utiliza para calcular el peso de cada criterio, han demostrado ser métodos adecuados para validar la selección de materiales [5, 6].
En los últimos 3 años la demanda de vehículos SUV en el Ecuador de la marca Chevrolet ha incrementado en un 7 %, siendo el modelo Suzuki Grand Vitara SZ 2.0 el quinto vehículo más vendido según la Asociación de Empresas Automotrices del Ecuador [7]. Teniendo en cuenta que en el Ecuador se está incentivando la inclusión del producto nacional, es importante seleccionar un material existente en el país para la fabricación del disco de freno junto con el análisis costo/beneficio. El objetivo de este estudio es evaluar un material alterno en la fabricación de un disco de freno en vehículos livianos tipo SUV, a partir de los métodos multicriterio COPRAS, VIKOR, ELECTRE I, ARAS, MOORA y el de ENTROPÍA.
Materiales y métodos
Definición del problema
Se ha desarrollado diferentes tipos de aleaciones para el diseño y fabricación de discos de freno en la industria automotriz, porque deben cumplir parámetros extremadamente altos, debido a que este dispositivo trabaja a altos grados de desgaste y temperatura.
Los discos de hierro fundido gris tienen mejor resistencia al desgaste que los de aleaciones o compuestos de Ti, sin embargo, la adición de partículas duras a un compuesto con base de Ti puede mejorar sustancialmente la resistencia al desgaste [8]. El análisis de las propiedades mecánicas entre una aleación de aluminio, hierro fundido, aleación de titanio, materiales cerámicos y compuestos condujo como resultado el material más apropiado para la fabricación de un disco de freno a una aleación de aluminio [9]. Una alternativa a los metales son los materiales compuestos como la fibra de vidrio de alta resistencia, que tiene una mayor resistencia al desgaste y menor peso [10].
Entre las propiedades importantes que el material a seleccionar debe tener es la conductividad térmica. Un valor alto permite disipar el calor rápidamente y un coeficiente de expansión térmico alto permite tener una buena dilatación térmica al exponer el disco de freno a una variación de temperatura.
Además, un buen límite elástico, módulo de Young y un coeficiente de Poisson, permitirán soportar altas tensiones sin sufrir deformaciones permanentes en el disco. Un valor alto de resistencia a la compresión, tracción y dureza Brinell, evitará que el material se fracture debido a los esfuerzos producidos por las mordazas al momento del frenado. Para disminuir el consumo del vehículo es necesario reducir el peso del vehículo, por tal razón el disco de freno debe tener una baja densidad. Es importante realizar un análisis costo-beneficio del material seleccionado.
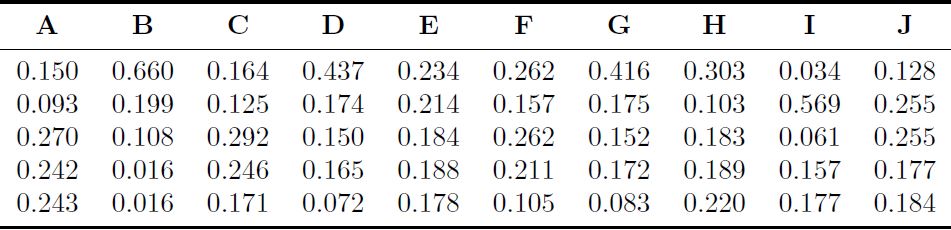
Tomando en cuenta todos estos criterios los materiales candidatos para la fabricación de discos de freno en el Ecuador son los siguientes: Ti 6Al 4V (aleación de titanio, número 1), Al 10Si C (aleación de aluminio o Duralcan, número 2), AISI 304L (acero inoxidable, número 3), ASTM A536 (fundición gris nodular, número 4) y ASTM A48 (fundición gris perlítico, número 5).
Métodos multicriterio. Criterios de ponderación
Los métodos multicriterios empleados son el COPRAS, VIKOR, ELECTRE I, ARAS y MOORA. El cálculo de los pesos de cada criterio se lo realiza a través del método entropía, con el objeto de contar con resultados objetivos ya que parte del supuesto de que un criterio tiene mayor peso cuando mayor diversidad hay en la evaluación de cada alternativa.
Método entropía
La entropía mide la incertidumbre en la información formulada usando la teoría de la probabilidad. Indica que una distribución amplia representa más incertidumbre que la de una distribución con picos pronunciados. El método entropía se calcula en los siguientes pasos [11]:
Paso 1: Construcción de la matriz de decisión.
Paso 2: Cálculo de la matriz de decisión normalizada Pij, el objetivo de la normalización es obtener valores sin dimensiones de diferentes criterios para hacer comparaciones entre ellos [11]. Se calcula usando la Ecuación (1).
Paso 3: Cálculo de la entropía Ej, mediante la Ecuación (2)
Donde k = 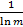 es una constante que garantiza 0
es una constante que garantiza 0 Ej
Ej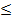 1 y m es el número de alternativas.
1 y m es el número de alternativas.
Paso 4: Cálculo de la diversidad de criterio Dj, la Ecuación (3) permite calcular este parámetro.
Paso 5. Cálculo del peso normalizado de cada criterio Wj, mediante la Ecuación (4).
Método COPRAS
El método COPRAS selecciona las mejores alternativas de decisión considerando las soluciones ideales y las peores-ideales, en una clasificación y evaluación paso a paso de las alternativas en términos de su importancia y grado de utilidad. El algoritmo del método COPRAS consta de los siguientes pasos [12]:
Paso 1: Cálculo de la matriz de decisión normalizada 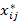 , mediante la Ecuación (5).
, mediante la Ecuación (5).
Paso 2: Determinar la matriz de decisión normalizada ponderada Dij, según la Ecuación (6).
Donde 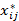 es el valor del rendimiento normalizado de ith
alternativas en jth
criterios y wj
es el peso asociado a los criterios jth.
es el valor del rendimiento normalizado de ith
alternativas en jth
criterios y wj
es el peso asociado a los criterios jth.
Paso 3: Las sumas Si+ y Si- de los valores normalizados ponderados, son calculadas tanto para los criterios beneficiosos como para los no beneficiosos respectivamente. Estas sumas Si+ y Si- son calculados mediante las Ecuaciones (7) y (8) respectivamente.
Paso 4: Determinar la importancia relativa de las alternativas Qi mediante la Ecuación (9).
La importancia relativa Qi de una alternativa muestra el grado de satisfacción alcanzada por esta alternativa.
Paso 5: Cálculo del índice de rendimiento Pi de cada alternativa, usando la Ecuación (10):
Donde Qmax es el valor máximo de importancia relativa. El valor del índice de rendimiento Pi se utiliza para obtener una clasificación completa de las alternativas candidatos.
Método VIKOR
El concepto básico de VIKOR consiste en definir primero las soluciones ideales positivas y negativas. La solución ideal positiva indica la alternativa con el valor más alto (puntuación de 100) mientras que la solución ideal negativa indica la alternativa con el valor más bajo (puntuación de 0) El algoritmo de compromiso VIKOR tiene los siguientes pasos [13]:
Paso 1: Definir la matriz de decisión inicial Xij .
Paso 2: Cálculo de la matriz de decisión inicial normalizada fij, utilizándola Ecuación (11).
Paso 3: Determinar el mejor y el peor valor de todas las funciones de criterio de cada alternativa. Mediante las Ecuaciones (12) y (13) respectivamente.
Paso 4: Cálculo de la distancia desde cada valor a la solución ideal positiva Si y la distancia desde cada valor a la solución ideal negativa Ri, mediante las Ecuaciones (14) y (15) respectivamente.
Paso 5: Cálculo de los valores Ii , para i = 1,…, I, está definido por la Ecuación (16).
Donde 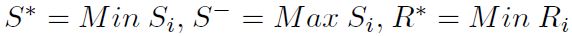 ,
, 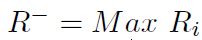 , y v es una referencia de ponderación
, y v es una referencia de ponderación  , representa la distancia de la solución ideal negativa de los valores i
th
.
, representa la distancia de la solución ideal negativa de los valores i
th
.
Paso 6: Se determina el ranking, el valor más alto es la mejor alternativa.
Método ELECTRE I
El método ELECTRE I tiene la capacidad de manejar criterios cuantitativos y cualitativos discretos y proporciona un orden completo de las alternativas. La limitación se reemplaza por la concordancia y discordancia del índice de la matriz. El procedimiento del método ELECTRE I es el siguiente [14]:
Paso 1: Definir la matriz de decisión inicial rij .
Paso 2: Normalización de la matriz de decisión, con tal proceso permitirá transformar diferentes escalas y unidades entre varios criterios comunes que permiten comparar a través de los criterios, según la Ecuación (17).
Paso 3: Construcción de la matriz de decisión ponderada normalizada Vij. Para lo cual se multiplica la matriz de decisión normalizada Rij con su respectivo peso, expresado en la Ecuación (18).
Paso 4: Cálculo de los intervalos de concordancia (Cab ) y discordancia (Dab ), es decir, Cab indica la alternativa más preferible y Dab indica la alternativa menos preferible. Se utilizan las Ecuaciones (19) y (20) respectivamente.
Paso 5: Determinación de la matriz de intervalo de concordancia Cab , se obtiene sumando los pesos a los pesos asociados a los criterios en los que la alternativa i es mejor que la alternativa j o viceversa; en caso de empate se asigna la mitad del peso a cada una de las alternativas según la Ecuación (21).
Paso 6: Determinación de la matriz de índice de discordancia Dab , se calcula como la diferencia mayor entre los criterios para los que las alternativas i está dominada por la j, dividiendo seguidamente por la mayor diferencia en valor absoluto entre los resultados obtenidos por la alternativa i y j, según la Ecuación (22).
Paso 7: Cálculo del umbral máximo 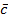 para el índice de concordancia y el umbral máximo
para el índice de concordancia y el umbral máximo 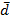 para el índice de discordancia, mediante las ecuaciones (23) y
para el índice de discordancia, mediante las ecuaciones (23) y  respectivamente.
respectivamente.
Paso 8: Cálculo de la matriz de concordancia dominante. Una vez que ya se determinó los índices de concordancia y el umbral mínimo de concordancia, la matriz de concordancia dominante se calcula con la siguiente condición:
Paso 9: Cálculo de la matriz discordante dominante. De igual manera que la anterior, los valores de la matriz de discordancia dominante, se obtiene de la matriz de índice de discordancia y el umbral máximo de discordancia . Mediante la condición siguiente:
Paso 10: Cálculo del valor neto superior e inferior Ca y Da , mediante las Ecuaciones (25) y (26) respectivamente.
Método ARAS
El método ARAS determina la eficiencia relativa compleja de una alternativa factible es directamente proporcional al efecto relativo de los valores y ponderaciones de los principales criterios considerados. Basándose en la teoría de la utilidad y en el método cuantitativo. Los pasos de este método son los siguientes [15].
Paso 1: Conformación de la matriz de decisión Xij ,
Paso 2: Cálculo de la matriz de decisión normalizada 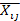 , teniendo en cuenta los valores beneficiosos se calcula con la Ecuación (27).
, teniendo en cuenta los valores beneficiosos se calcula con la Ecuación (27).
Para los criterios no-beneficiosos se calcula mediante la Ecuación (28).
Paso 3: Cálculo de la matriz de decisión normalizada ponderada se calcula con la Ecuación (29).
Los valores de peso Wj se determinan mediante el método entropía.
Donde Wj
es el peso del criterio j y 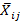 es la clasificación normalizada de cada criterio.
es la clasificación normalizada de cada criterio.
Paso 4: Cálculo de la función de optimización Si usando la Ecuación (30).
Donde Si
es el valor de la función de optimización de la i alternativa. Este cálculo tiene una relación directamente proporcional con el proceso de los valores 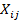 y pesos Wj
de los criterios investigados y su influencia relativa en el resultado final.
y pesos Wj
de los criterios investigados y su influencia relativa en el resultado final.
Paso 5: Cálculo del grado de utilidad. Este grado se determina comparando la variante que está en análisis con la mejor So , según la Ecuación (31).
Donde Si y So son los valores de la función de optimización. Dichos valores van desde 0 a 100 %, por lo tanto, la alternativa con el Ki más alto es la mejor de las alternativas analizadas.
Método MOORA
El método MOORA parte de puntos de referencia. Estas referencias serán la mayor evaluación del vector de radios de alternativas respecto de cada criterio ya sea máximo o mínimo. Los pasos de este método se describen de la siguiente manera [16].
Paso 1: Determinación de la matriz inicial de decisión Xij .
Paso 2: Cálculo de la matriz de radios de la forma 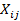 =
= 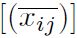 para normalizar la matriz de decisión inicial, se usa la Ecuación (32).
para normalizar la matriz de decisión inicial, se usa la Ecuación (32).
Paso 3: Se define el vector de pesos de los criterios.
Paso 4: Cálculo de la matriz normalizada por pesos. Se pondera multiplicando la matriz de dedición normalizada por los pesos de cada criterio.
Paso 5: Se determina la función de agregación para evaluar cada alternativa S(xi), utilizando la Ecuación (33).
Donde i = 1, 2, 3, …, h corresponde a los criterios catalogados como máximo; i = h+1, h+2, … n corresponde a los criterios catalogados como mínimo.
Paso 6: Se determina el ranking de preferencias. La mejor alternativa es la que tiene el valor S(xi) más alto.
Resultados y discusión
Aplicación del método entropía
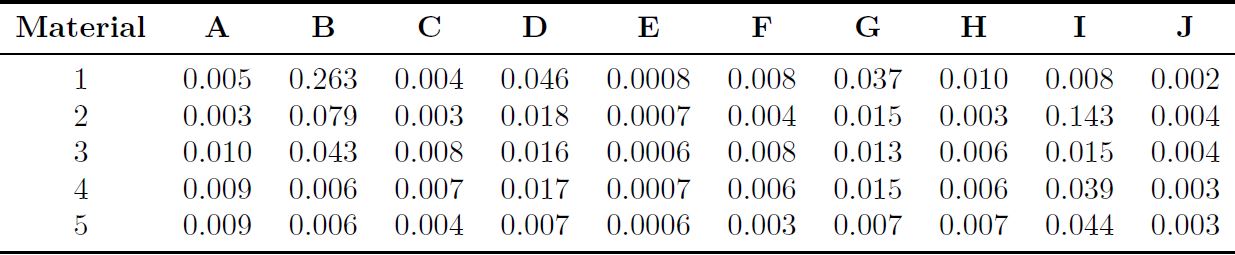
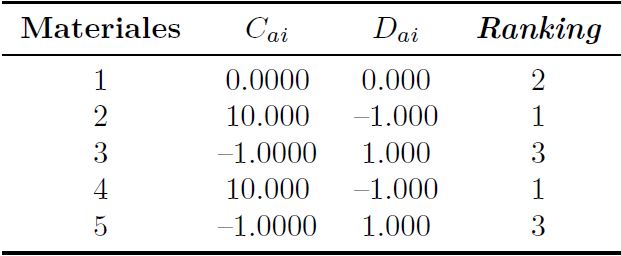
Los materiales candidatos y los criterios en análisis se muestran en la Tabla 1. Las propiedades de las alternativas son: densidad (A), precio (B), módulo de Young (C), límite elástico (D), radio de Poisson (E), resistencia a la tracción (F), resistencia a la compresión (G), dureza Brinell (H), conductividad térmica (I) y coeficiente de expansión térmica (J). Se aplica el método entropía para los criterios de ponderación, con el fin de obtener pesos objetivos al momento de la evaluación, puesto que el mismo se basa en modelos matemáticos definidos; a diferencia del método AHP que se basa en criterios de expertos aplicado por [14].
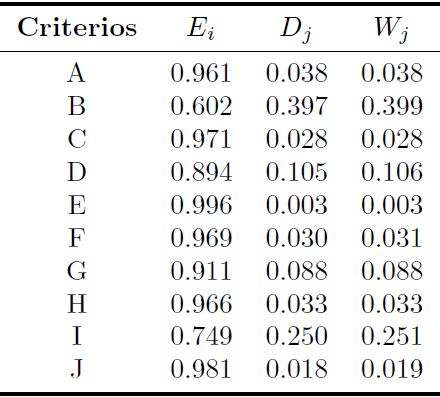
En la Tabla 2 se muestra la matriz de decisión normalizada del método entropía, que se calcula según la Ecuación (1). Los valores de la entropía Ej de cada variable, la diversidad de criterio (Dj) y los pesos normalizados de cada criterio (Wj) se indica en la Tabla 3, según las ecuaciones (2), (3) y (4) respectivamente.
COPRAS
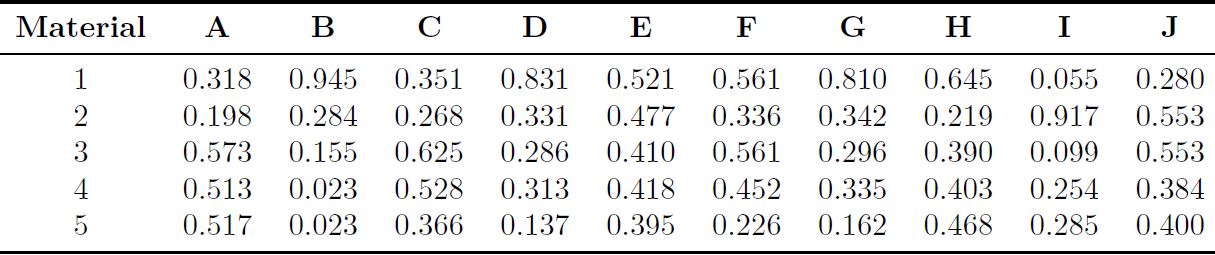
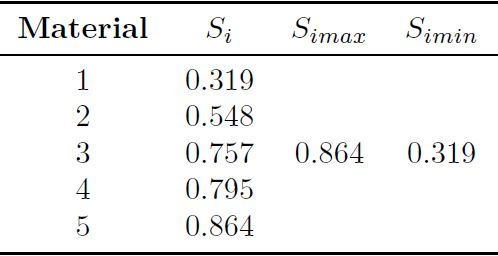
La matriz de decisión normalizada ( ), se calcula con la Ecuación (5), mientras que la matriz normalizada por pesos (Dij
) se calcula según la Ecuación (6) representado en la Tabla 4. La suma de los valores normalizados ponderados (Si+
), (Si-
) la importancia relativa (Qi
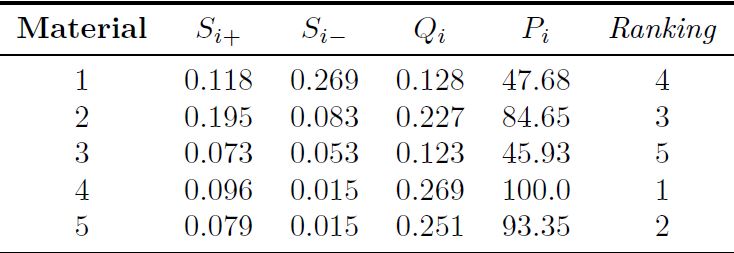
) muestra el grado de satisfacción de una alternativa y el índice de rendimiento (Pi) que determina el ranking de los materiales candidatos para la manufactura de un disco de freno, se calculan con las Ecuaciones (7), (8), (9) y (10) respectivamente y todos estos cálculos se indica en la Tabla 5, donde el mejor material es el 4 (ASTM A536) debido a la selección de las mejores alternativas de decisión relacionada con el módulo de Young (C), límite elástico (D), radio de Poisson (E), resistencia a la tracción-compresión (F y G), dureza (H) y conductividad térmica (I).
), se calcula con la Ecuación (5), mientras que la matriz normalizada por pesos (Dij
) se calcula según la Ecuación (6) representado en la Tabla 4. La suma de los valores normalizados ponderados (Si+
), (Si-
) la importancia relativa (Qi
) muestra el grado de satisfacción de una alternativa y el índice de rendimiento (Pi) que determina el ranking de los materiales candidatos para la manufactura de un disco de freno, se calculan con las Ecuaciones (7), (8), (9) y (10) respectivamente y todos estos cálculos se indica en la Tabla 5, donde el mejor material es el 4 (ASTM A536) debido a la selección de las mejores alternativas de decisión relacionada con el módulo de Young (C), límite elástico (D), radio de Poisson (E), resistencia a la tracción-compresión (F y G), dureza (H) y conductividad térmica (I).
VIKOR
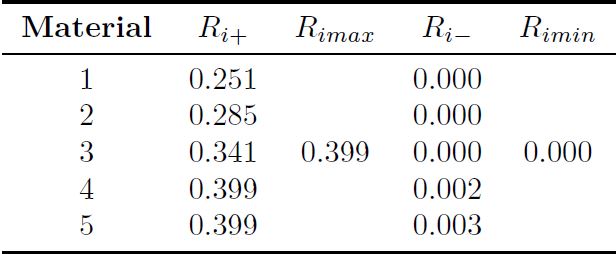
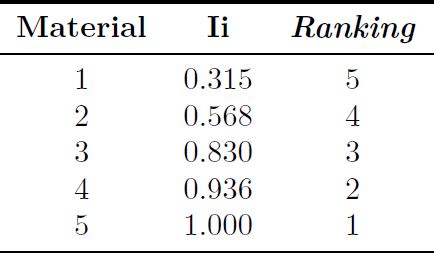
La matriz de decisión inicial normalizada fij se presenta en la Tabla 6, estos valores se obtienen mediante la Ecuación (11). El mejor y peor valor se determina con las Ecuaciones (12) y (13) respectivamente, los cuales se expone en la Tabla 7. Los valores de la distancia desde cada valor a la solución positiva (Si ), se calcula según la Ecuación (14), se indica en la Tabla 8 y la distancia a la solución ideal negativa (Ri ), se calcula con la Ecuación (15), que se denota en la Tabla 9. El valor de (Ii ) se obtiene mediante la Ecuación (16), el valor más alto de (Ii ) determina el mejor material en este caso es un ASTM A48 (número 5). Estos valores se indican en la Tabla 10, debido a su baja densidad (A), bajo radio de Poisson (E) y una elevada dureza Brinell (H).
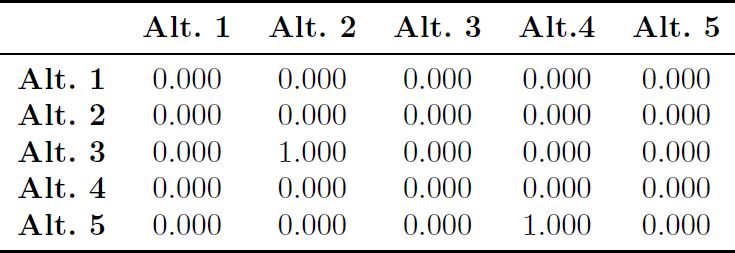
ELECTRE I
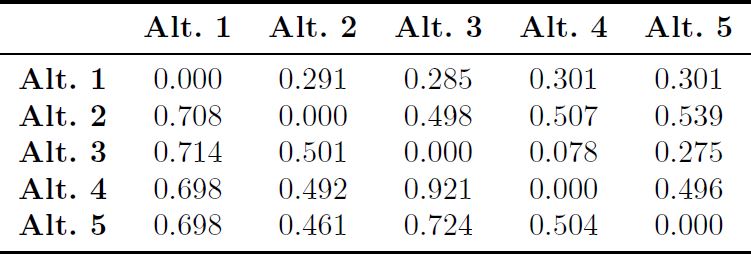
Los datos de la matriz de decisión inicial se tabulan en la Tabla 1 y la matriz de decisión normalizada ponderada (Vij
) se obtiene utilizando la Ecuación (18), dichos valores se indican en la Tabla 11. La matriz de intervalos de concordancia (Cab
), se calcula según la Ecuación (19) y se representa en la Tabla 12. Mediante la Ecuación (20) se calcula los valores de matriz de intervalos de discordancia (Dab
), los cuales están tabulados en la Tabla 13. El umbral máximo (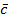 ) para el índice de concordancia, se determina con la Ecuación (23) y la matriz de concordancia dominante (
) para el índice de concordancia, se determina con la Ecuación (23) y la matriz de concordancia dominante (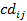 ) se representa en la Tabla 14. Mientras el umbral máximo para el índice de discordancia (
) se representa en la Tabla 14. Mientras el umbral máximo para el índice de discordancia (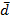 ), se calcula según la Ecuación (24), tabulados en la Tabla 15 y la matriz discordante (
), se calcula según la Ecuación (24), tabulados en la Tabla 15 y la matriz discordante ( ) se expone en la Tabla 16. Por último, el valor neto superior e inferior (Ca
) y (Cb
), se obtiene según las ecuaciones (25) y (26) respectivamente, estos valores se muestran en la Tabla 17. El material con mejor puntuado es el ASTM A536. Los materiales con mejor puntuación son el Al 10 Si C (número 2) y el ASTM A536 (número 4), incidiendo la conductividad térmica (I), límite elástico (D) y la resistencia a la tracción-compresión (F y G).
) se expone en la Tabla 16. Por último, el valor neto superior e inferior (Ca
) y (Cb
), se obtiene según las ecuaciones (25) y (26) respectivamente, estos valores se muestran en la Tabla 17. El material con mejor puntuado es el ASTM A536. Los materiales con mejor puntuación son el Al 10 Si C (número 2) y el ASTM A536 (número 4), incidiendo la conductividad térmica (I), límite elástico (D) y la resistencia a la tracción-compresión (F y G).
ARAS
Según la Ecuación (27) se calcula la matriz de decisión normalizada (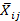 ), teniendo en cuenta el cálculo de los valores no-beneficiosos mediante la Ecuación (28). Posteriormente, la matriz de decisión normalizada por pesos (
), teniendo en cuenta el cálculo de los valores no-beneficiosos mediante la Ecuación (28). Posteriormente, la matriz de decisión normalizada por pesos (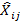 ) se define por la Ecuación (29), cuyos valores se presenta en la Tabla 18. Utilizando la Ecuación (30) para calcular los valores de la función de optimización (Si
) de cada una de las alternativas, el grado de utilidad (Ki
) se calcula mediante la Ecuación (31), la cual determina el ranking de las alternativas para la aplicación en estudio. Estos valores se representan en la Tabla 19, mostrándose que el material ASTM A536 (número 4) es el mejor a consecuencia del efecto relativo de los valores de conductividad térmica, límite elástico y resistencia a la compresión.
) se define por la Ecuación (29), cuyos valores se presenta en la Tabla 18. Utilizando la Ecuación (30) para calcular los valores de la función de optimización (Si
) de cada una de las alternativas, el grado de utilidad (Ki
) se calcula mediante la Ecuación (31), la cual determina el ranking de las alternativas para la aplicación en estudio. Estos valores se representan en la Tabla 19, mostrándose que el material ASTM A536 (número 4) es el mejor a consecuencia del efecto relativo de los valores de conductividad térmica, límite elástico y resistencia a la compresión.
MOORA
La matriz de decisión (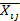 ) se obtiene según la Ecuación (32). La Tabla 20 muestra la matriz de decisión normalizada ponderada. Luego se obtiene la función de agregación S(xi) que evalúa cada alternativa, mediante la Ecuación (33), además, este cálculo determina el ranking de preferencia de cada alternativa. Los valores se muestran en la Tabla 21, mostrándose que el material Al 10Si C (número 2) es el mejor debido a que su conductividad térmica (I) y coeficiente de expansión térmica (J) son altos respecto al resto de los materiales experimentados.
) se obtiene según la Ecuación (32). La Tabla 20 muestra la matriz de decisión normalizada ponderada. Luego se obtiene la función de agregación S(xi) que evalúa cada alternativa, mediante la Ecuación (33), además, este cálculo determina el ranking de preferencia de cada alternativa. Los valores se muestran en la Tabla 21, mostrándose que el material Al 10Si C (número 2) es el mejor debido a que su conductividad térmica (I) y coeficiente de expansión térmica (J) son altos respecto al resto de los materiales experimentados.
EVALUACIÓN DE LOS MCDM
Los MCDM tienen la tarea de clasificar un número finito de alternativas de decisión, cada una se describe explícitamente en términos de diferentes criterios de decisión que deben tenerse en cuenta simultáneamente. Por tal razón, se utiliza estos métodos en la selección del material para la construcción de un disco de freno.
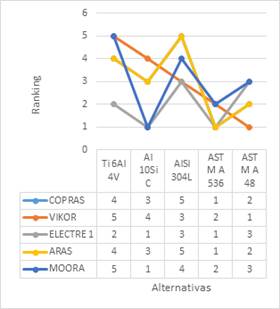
En la Figura 1 se muestra el ranking de todos los métodos MCDM, con la observación que el método COPRAS y ARAS tienen los mismos valores de ranking, por lo cual sus curvas se superponen.
El mejor material en los métodos COPRAS, ELECTRE I, y ARAS es ASTM A536, por su baja densidad (A), un alto límite elástico (D) y una buena resistencia a la compresión (G), el método MOORA y VIKOR lo ubican como una segunda alternativa. La segunda mejor opción evaluada es el Al 10Si C y el ASTM A48 por los criterios de ELECTRE I, MOORA y VIKOR, ya que tiene buena conductividad térmica (I), baja densidad (A) y un precio accesible (B). Estos resultados están alineados con los materiales empleados en el estudio realizado por Maleque, Dyuti, & Rahman [9], además, Kharate & Chaudhari [17] estudian el efecto de las propiedades del material en el ruido y el rendimiento del disco de freno mediante el enfoque FEM y EMA, para lo cual experimentan con fundición gris, carbón cerámico y acero, obteniéndose como resultado que la fundición gris tiene una frecuencia natural más baja que el resto de los materiales experimentados.
Conclusiones
Los métodos MCDM empleados en esta investigación, permitieron la selección de un material para la fabricación de un disco de freno, incorporando criterios cuantitativos y cualitativos. La ponderación de las propiedades de los materiales candidatos para la construcción de un disco de freno se obtuvo por el método ENTROPÍA. Según los métodos COPRAS, ELECTRE I y ARAS el mejor material es el ASTM A536, con mejores propiedades térmicas y mecánicas. En una segunda opción según los criterios de ELECTRE I, MOORA y VIKOR son el Al 10Si C y el ASTM A48. Las técnicas MCDM permiten resolver problemas complejos, que se adaptan a cualquier tipo de necesidad y se aplican a las diferentes áreas de la ingeniería.
Referencias