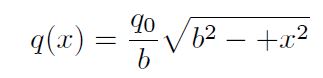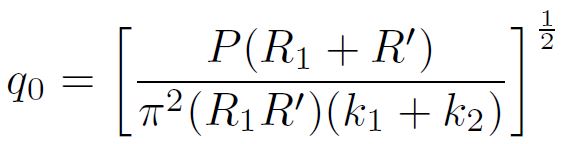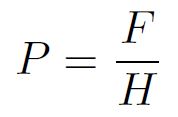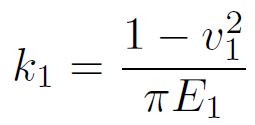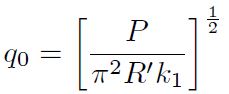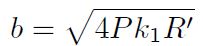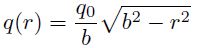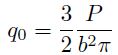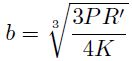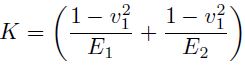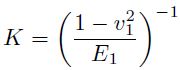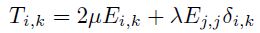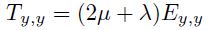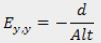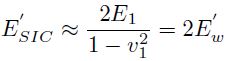Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Las articulaciones humanas de rodilla y cadera permiten el movimiento relativo entre los huesos que las componen, fémur y tibia en el primer caso, cadera y fémur en el segundo.
Siendo el desgaste el principal factor limitante de la vida útil de los implantes de rodilla y cadera [1], y ante la necesidad de prótesis más duraderas evidenciada en el incremento de artroplastias de revisión proyectadas para el año 2030 [2, 3], el estudio de la mecánica del contacto articular adquiere gran importancia.
Tanto en las articulaciones sanas como en las protésicas, las superficies articulares están lubricadas por líquido sinovial y el régimen de lubricación depende, entre otros factores, de la deformación que sufren las superficies articulares en contacto.
Numerosos estudios del contacto lubricado en articulaciones humanas expresan los desplazamientos que sufren las superficies articulares mediante modelos aproximados que simplifican el sistema de ecuaciones reduciendo el esfuerzo computacional para resolverlo [4, 5]. Estos modelos son válidos para materiales elásticos lineales de baja rigidez y de «pequeño espesor» (layer en inglés), en los cuales la dimensión en la dirección de la carga es al menos un orden de magnitud menor que las otras dimensiones [6]. En tal caso, el desplazamiento en un punto de la superficie del sólido, se asimila al de una columna aislada (no conectada con su entorno) de un material que posee propiedades elásticas expresadas a través de un módulo elástico o de Young, denominado equivalente.
Pueden mencionarse tres módulos de Young equivalentes que pueden incluirse en los modelos de desplazamiento de columna y que son objeto de análisis y comparación en este trabajo: el módulo de Young equivalente que surge de considerar un sólido de pequeño espesor [6], y dos módulos de Young denominados de Winkler [7] y semiinfinito corregido (SIC) ambos derivados de considerar un sólido semiinfinito.
En este trabajo se evalúan casos representativos de articulaciones sanas y protésicas, aplicando los tres módulos elásticos mencionados, y los resultados obtenidos se comparan con los arrojados por la solución del problema elástico en el material, a través de la resolución de la ecuación diferencial de elasticidad lineal, utilizando cálculo numérico basado en el método de elementos finitos (MEF). Esta solución se asume como la solución exacta [8].
Si bien las articulaciones de rodilla y cadera, sanas y protésicas, se encuentran lubricadas por el fluido sinovial, suelen considerarse como un contacto seco y estático [9, 10], observándose en algunos casos perfiles de presión prácticamente iguales que los obtenidos a partir de modelos elastohidrodinámicos [11]. Por lo tanto, en este trabajo se aplica en todos los casos una carga hertziana.
Todos los problemas de contacto son inherentemente no lineales ya que el área de contacto depende, en forma no lineal, de la carga [9, 12]. En el presente trabajo se considera una geometría de tipo cilindro sobre plano (del inglés CoP, situación de contacto lineal) equivalente a la rodilla y una geometría de tipo esfera sobre plano (del inglés SoP, situación de contacto puntual) equivalente a la cadera [13, 14, 15].
El presente artículo es producto de las actividades de formación y entrenamiento en las artes de la Mecánica Computacional de un alumno avanzado de la carrera de Bioingeniería, en tanto becario de iniciación a la investigación del proyecto marco en el que se inscribe este trabajo.
Materiales y métodos
Modelo CoP
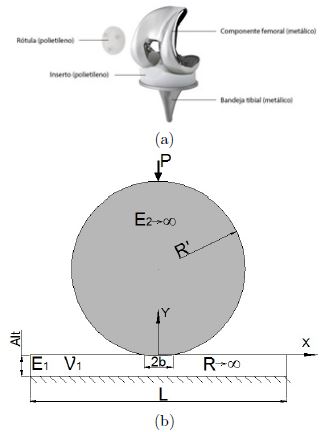
La articulación de rodilla, tanto la natural como la protésica, puede abstraerse físicamente como un cuerpo cilíndrico lleno en contacto lineal con un cuerpo cilíndrico hueco. En tal abstracción se desprecia la curvatura en la dirección medial-lateral de los elementos en contacto (componentes tibial y femoral). Adicionalmente, cuando la región de contacto es pequeña en comparación con el radio de los cilindros, el contacto entre dos rodillos puede representarse por el contacto de un rodillo equivalente y un plano. El cilindro equivalente (ver Figura 1) tiene la curvatura combinada de los cilindros considerados inicialmente, es decir, en este caso el radio R’ se obtiene a partir de los radios del cóndilo femoral (o componente femoral, R2 ) y el radio del platillo tibial (o componente tibial, R1 ). En la Figura 1.b se observa la representación equivalente y el sistema de ejes coordenados, siendo el eje x coincidente con la dirección antero-posterior (y de movimiento de la rodilla), el eje y coincide con la dirección de aplicación de la carga y el eje z con la dirección medial-lateral.
La razón fundamental de esta aproximación geométrica es la posibilidad de plantear para el problema elástico y también en el caso del contacto lubricado, un modelo de flujo en coordenadas cartesianas [16, 17]. Esta descripción es más simple de resolverse, no solo analíticamente en algunos casos, sino también numéricamente.
El contacto lineal produce un estado de deformaciones planas independiente de la dirección medial-lateral. En este trabajo se define como H a la longitud de una articulación de rodilla en esta dirección (ver Tabla 1).
De acuerdo con lo expresado, la articulación de rodilla puede modelarse como un cilindro indeformable sobre un sólido plano de baja rigidez como el representado en la Figura 1.b. El espesor del sólido plano representará el espesor conjunto de los cartílagos naturales en una articulación sana (ver sección 2.5). Para el caso de la articulación protésica el material deformable es polietileno de ultra alto peso molecular (del inglés UHMWPE), que posee un módulo de elasticidad 100 veces menor al del componente femoral ya que en general este se fabrica de una aleación de titanio o acero inoxidable de grado médico (AISI 316L entre otros).
Carga hertziana
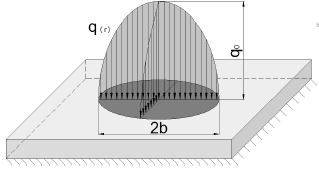
La carga hertziana actuante para el contacto seco de la Figura 1-b [16], sigue una distribución en forma de semielipse para la carga específica por unidad de área, como muestra la Ecuación (1):
Donde q 0 es la carga específica máxima por unidadde área, actuante en el centro del contacto, es decir,en el centro del segmento de longitud 2b, y está dada por:
P es la carga por unidad de longitud en la dirección del eje del cilindro. El valor de P está dado por la relación entre la carga total F sobre el contacto y la longitud del cilindro H:
El término 
se toma como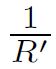 
por tender 
a infinito.
Las constantes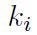 
de la Ecuación 2 contienen las propiedades del material elástico lineal: el módulo de Young y el coeficiente de Poisson. Dados los parámetros de la figura 1-b, 
resulta nula, luego:
Finalmente, la carga q0 queda definida por:
El semiancho b del contacto está dado por:
y teniendo en cuenta las consideraciones previas
donde el radio R’ [16] viene dado por:
Modelo SoP
La articulación de cadera o coxofemoral puede abstraerse físicamente como un cuerpo esférico lleno en contacto puntual con un cuerpo esférico hueco como se muestra en la Figura 2-a. Este modelo geométrico usualmente se denomina de tipo esfera-en-casquete (ball-in-socket) y se caracteriza por el radio de la cabeza femoral (superficie esférica convexa), el radio del acetábulo (superficie esférica cóncava), y el espacio entre ambas superficies (clearence c*). Las ecuaciones que gobiernan este modelo se expresan en coordenadas esféricas, por lo tanto, requieren un análisis en 3 dimensiones [11].
Un modelo equivalente, que permite expresar las ecuaciones gobernantes en coordenadas cartesianas –y simplificar su resolución al convertirlo en un problema en 2 dimensiones–, es el denominado esfera-sobre-plano (ball-on-plane) que se muestra en la Figura 2-b [18].
Tanto una articulación de cadera sana como una protésica pueden modelarse geométricamente como una esfera sobre un plano deformable. Esta aproximación es válida cuando se trata de regiones de contacto pequeñas en comparación con el radio de las superficies esféricas. La esfera equivalente tiene un radio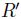 
que se obtiene a partir del radio de la cabeza femoral (
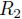) y del radio interior del acetábulo (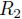), de modo que la esfera en contacto con el plano posea la curvatura combinada de las esferas de la Figura 2-a.
Figura 2. La geometría posee simetría polar. (a) Prótesistotal de cadera [18]. Se destacan en rosa la cabeza femoral yel acetábulo. (b) Representación equivalente en un contactoSoP.
Estimación de la carga
Para la determinación de la carga en la superficie de contacto seco, se utilizó el modelo hertziano para una esfera sobre un plano.
Donde q 0 es la carga máxima por unidad de área,actuante en el centro de la superficie circular de contactode radio b.
P, en este caso, es la carga total ejercida sobre laesfera. El radio b, viene dado por:
siendo K
Dado que E2 es 2 órdenes de magnitud mayor que E1 , podría asumirse que E2 tiende a infinito, entonces K resulta:
Módulos elásticos equivalentes
Modelo de columna para material de pequeño espesor (PE)
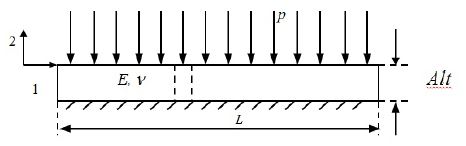
Este modelo se basa en suponer que el material deformable está compuesto de columnas de sección transversal a la carga (ver Figura 3) con tamaño diferencial. Cada columna se encuentra en contacto lateral con columnas de iguales características, siendo despreciables las fuerzas tangenciales entre ellas [6].
Asumiendo al sólido como elástico lineal, la relaciónentre tensiones (T) y deformaciones (E) está dada porla ley de Hooke que, en términos de las constantes deLamé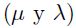 
y en notación indicial, se expresa:
donde 
es el delta de Kronecker y E y T son lostensores de deformaciones y tensiones respectivamente.Si se asume que el material considerado es elásticolineal, de baja rigidez y pequeño espesor, cargado acompresión en la dirección de su espesor (dirección y o 2 en índices), luego, la tensión normal en la dirección yes mucho mayor que las otras, que pueden por lo tantodespreciarse. Del mismo modo, son despreciables las deformaciones que no sean el acortamiento relativo en la dirección y. La ley de Hooke queda:
lo cual es equivalente a la ley de Hooke para una columna sola de módulo elástico (2μ + λ), luego (ver Figura 1.b):
Donde p es la tensión normal a las superficies en contacto, d es el desplazamiento superficial y Alt es el espesor del material de baja rigidez.
Donde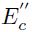 
es el módulo elástico equivalente, que en términos del módulo de Young (
E
1) y el coeficiente de Poisson (v
1) del componente tibial se expresa:
Módulo elástico equivalente de Winkler(W) y de sólido semiinfinito corregido (SIC)
El módulo equivalente de Winkler, surge del caso de un sólido limitado por un plano y con profundidad infinita en la dirección normal a dicho plano. En esa dirección normal actúa una carga de contacto distribuida sobre el plano, que produce desplazamientos en todo punto del sólido. El problema elástico se describe por una función potencial de la cual se obtienen las tensiones y, en virtud de la ley de Hooke, los desplazamientos en cada punto. La función potencial o función de Airy, posee una expresión para el contacto lineal y otra para el contacto puntual.
Para una distribución de carga, tanto para el caso de contacto lineal [16] como el de contacto puntual [17], los desplazamientos combinados de las superficies que delimitan dos sólidos distintos en contacto, son equivalentes a dos veces el desplazamiento de un sólido con un módulo elástico «reducido» o «equivalente», que vincula las propiedades elásticas de ambos sólidos:
En el caso particular en que ambos sólidos en contactosean iguales, el módulo equivalente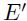 
toma la expresión (21) y se denomina de Winkler:
El módulo de Winkler es por tanto aplicable solo para el caso de articulaciones naturales, en donde ambas superficies corresponden al cartílago articular y ha sido utilizado en publicaciones científicas [7].
Como se discutió previamente, en el caso de las articulaciones protésicas, el módulo de elasticidad del componente femoral (E2) es 2 órdenes de magnitud mayor que E1, entonces el módulo de elasticidad obtenido a partir de la Ecuación (20) resulta
Se denomina a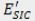 
módulo elástico equivalentede sólido semiinfinito corregido (SIC) dado que es otrocaso particular de la Ecuación (20).
Notar que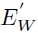 
y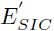 
son menores que 
para todos los valores de E y n que se consideren. De aquí, que uno de los objetivos de este trabajo es determinar la validez de utilizar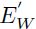 
, 
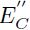y 
en una aplicación concreta.
Modelos de desplazamiento
Para determinar el desplazamiento que sufren las superficies en cada caso a analizar, se utilizó la expresión (18), para la cual la presión de contacto es la carga específica por unidad de área q del contacto hertziano. En el caso de la prótesis de rodilla la carga varía longitudinalmente con la coordenada transversal al eje del cilindro (Ecuación 1), mientras que para la articulación de la cadera, la carga varía radialmente (Ecuación 9). Luego, los desplazamientos en cada caso son:
Donde d es el desplazamiento de la superficie y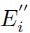 
es el módulo elástico equivalente, que se varía para el análisis entre los obtenidos para: material de pequeño espesor (
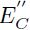) , sólido semiinfinito o de Winkler (
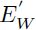) y sólido semiinfinito corregido (
).
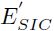Parámetros para la simulación de articulaciones de rodilla
Para el caso de articulaciones de rodilla se utilizaron los parámetros mostrados en la Tabla 1.
Usualmente se considera que la fuerza máxima promedio que soporta una articulación de la extremidad inferior es aproximadamente tres veces el peso corporal de la persona en la mayoría de las actividades diarias como caminar, subir escaleras y pararse en una pierna [19,20]. Considerando una persona con una masa corporal (MC) de 80 kg, la carga total F sobre el contacto será 2352 [N] (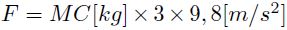
). La carga por unidad de longitud P se calcula de acuerdo con la Ecuación (3), asumiendo que la longitud del cilindro H es de 0,03 [m].
Para la articulación sana el módulo de elasticidad del cartílago articular es de 10 MPa [21], y para el caso de la articulación protésica, este es de 1 GPa para el UHMWPE [18]. Tanto el cartílago como el UHMWPE poseen un coeficiente de Poisson de 0,4.
Para esta simulación se utilizan tres espesores para el material deformable: 1,2, 2 y 2,5 mm para el espesor conjunto de ambas capas de cartílago [22] y 8, 10 y 12 mm para el caso de la articulación protésica hecha de UHMWPE [24].
Articulación de cadera
Para el caso de articulaciones de cadera se utilizaron los parámetros mostrados en la Tabla 2.
Al igual que en el caso de la articulación de rodilla, se considera una persona con una masa corporal (MC) de 80 kg y la carga total soportada por la articulación es aproximadamente 3 veces el peso corporal de la persona [24].
Debe aclararse que la constante c* es la diferencia entre el radio del acetábulo y el radio de la cabeza femoral (R2-R1).
Para esta simulación se utilizan tres espesores para el material deformable: 1,2, 2 y 2,5 mm para el espesor conjunto de ambas capas de cartílago y 8, 10 y 12 mm para el caso de la articulación protésica hecha de UHMWPE.
Obtención de resultados mediante MEF
El cálculo por elementos finitos se realiza utilizando el módulo de Mecánica Estructural del software con licencia COMSOL Multiphysics 5.3. Las geometrías analizadas se discretizaron con elementos Lagrange cuadráticos, tetraédricos para los volúmenes y triangulares para las superficies. En cualquier caso y en las geometrías correspondientes, la ecuación diferencial de elasticidad lineal y las ecuaciones de compatibilidad, precargadas en el módulo de Mecánica Estructural, se resolvieron utilizando el resolvedor directo MUMPS, disponible en COMSOL Multiphysics. Las condiciones de contorno empleadas se describen seguidamente.
Para la articulación de la rodilla la simulación se realiza en un dominio 2D (señalado en gris en la Figura 4) ya que la carga no varía en la dirección del eje del cilindro. Las condiciones de contorno se establecen de la siguiente forma: los bordes L1 , L3 , L4 y L5 se definen como libres de tensión, L6 se establece fijo, es decir, con desplazamientos nulos, y en el borde L2 la tensión actuante es la carga hertziana específica q(x) definida en la Ecuación (1) (Figura 4). Debe notarse que el dominio utilizado es mayor que el sector de interés (el limitado por L2 ), debido a que el elevado coeficiente de Poisson de los materiales simulados hace que estos actúen casi como incompresibles, deformándose en el sentido opuesto en parte de los sectores L1 y L3 . Por ello un dominio mayor permite que la simulación pueda cumplir con las condiciones de contorno impuestas.
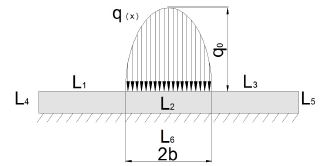
Figura 4. Esquema del dominio para articulación de rodilla donde se resuelve el problema elástico mediante el MEF. Se presentan los bordes donde se aplican distintas condiciones de borde.
En el caso de la articulación de la cadera la simulación se realiza en un dominio 3D (señalado en gris en la Figura 5) debido a que la carga varía radialmente.
Para este caso la base del prisma que representa el material deformable se estableció fija y el resto de las caras están libres de tensiones, excepto el círculo central, de diámetro 2b, en donde se ejerce la carga. Allí, la tensión actuante es la carga hertziana específica q(r) definida en la Ecuación (9).
Resultados y discusión
Articulación de rodilla
Para el caso de la articulación sana, donde se suponen dos capas de material delgado recubriendo los cóndilos femorales y el platillo tibial, los resultados de desplazamiento de las superficies en contacto se muestran en la Figura 6. Cabe destacar que los desplazamientos totales de ambos recubrimientos, son iguales al de uno solo con el doble del espesor (ver Ecuación 23). Por ello, los resultados que se muestran en la Figura 6, corresponden a un sólido con el espesor de dos cartílagos.
Deben destacarse en la Figura 6 los desplazamientos positivos que predice la solución MEF tomada como exacta, debido a la cuasi incompresibilidad del material supuesto debido al elevado valor del coeficiente de Poisson, tal como se ha comentado en el ítem 2.6.
Mientras el modelo simplificado con el módulo elástico equivalente de Winkler estima desplazamientos excesivamente mayores al dado por la solución MEF, los cálculos utilizando el módulo elástico equivalente de sólido semiinfinito corregido los subestima para los casos analizados. Los resultados para el modelo simplificado con el módulo elástico equivalente correspondiente al sólido de pequeño espesor son los que mejor aproximación tienen respecto a los valores arrojados por la solución MEF, en la Figura 6 se ven superpuestas las curvas para PE y MEF.
En la Tabla 3 por su parte, se muestran los desplazamientos máximos obtenidos para cada módulo elástico equivalente y el valor obtenido por la solución MEF. En la Tabla 4 se muestran las diferencias porcentuales correspondientes a la Tabla 3, siempre respecto a la solución MEF.
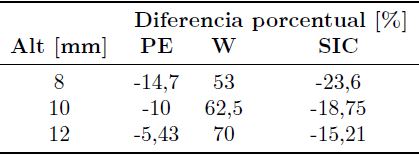
En la Figura 7 se observan los resultados obtenidos para el caso de la prótesis de rodilla. En la Tabla 5 se muestran los desplazamientos máximos para cada módulo elástico equivalente y el obtenido mediante MEF. En la Tabla 6 se muestra la diferencia porcentual correspondiente.
Es notoria la sobrestimación de los desplazamientos cuando se utiliza el módulo de Young equivalente de Winkler en el caso de la prótesis y esto se debe a que este módulo de elasticidad corresponde a un caso particular del módulo de elasticidad equivalente para sólido semiinfinito en donde ambas superficies en contacto tienen las mismas propiedades mecánicas, lo cual no sucede en articulaciones protésicas. Sin embargo, la validez del módulo de Winkler aplicado a articulaciones sanas (Figura 6) también queda en tela de juicio ya que asume un sólido semiinfinito y no una capa delgada como realmente ocurre con los cartílagos naturales.
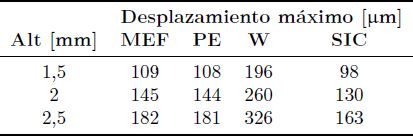
Tabla 3. Desplazamiento máximo obtenido por el MEF y para el modelo simplificado con cada módulo elástico equivalente considerado para articulación de rodilla natural
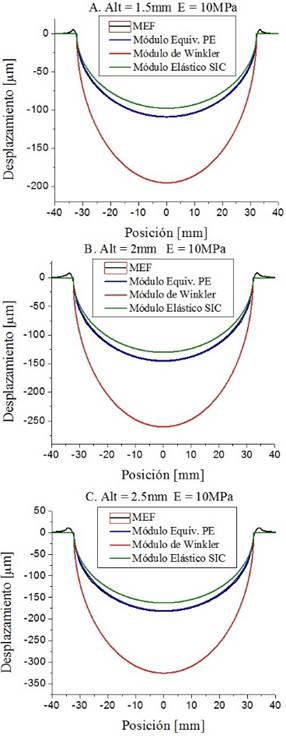
Figura 6. Comparación de las curvas de desplazamiento de las superficies en contacto obtenidas para cada módulo elástico equivalente, en contraste con la solución obtenida por el MEF en el caso de una articulación sana.
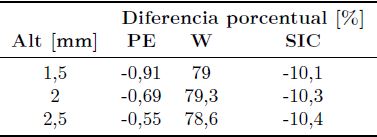
Tabla 4. Diferencia porcentual de los resultados PE, W y SIC respecto al obtenido por MEF para articulación de rodilla natural
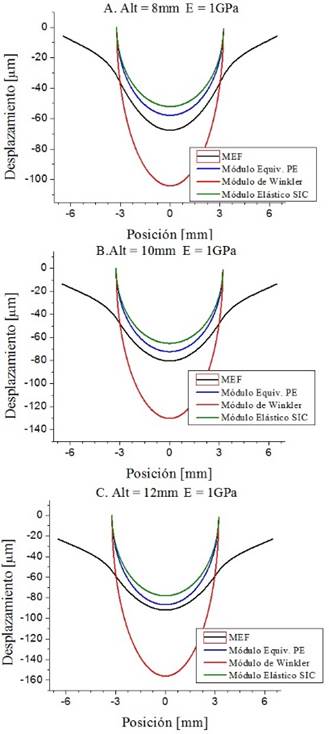
Figura 7. Comparación de las curvas de desplazamiento de las superficies en contacto obtenidas para cada módulo elástico equivalente, en contraste con la solución obtenida por el MEF en el caso de una articulación protésica.
Tabla 5. Desplazamiento máximo obtenido por MEF y para el modelo simplificado con cada módulo elástico equivalente considerado en prótesis de rodilla
La comparación de los resultados de las Figuras 6 y 7, también muestran el empobrecimiento de la aproximación de sólido de pequeño espesor cuando el módulo elástico del material y el espesor del material aumentan. Vale destacar que el módulo de Young del UHMWPE es 100 veces mayor que el correspondiente a los cartílagos naturales.
Articulación de la cadera
Para la articulación de cadera sana, donde también se suponen dos recubrimientos de igual espesor para los cuales los desplazamientos se suman, se obtuvieron las superficies de las Figuras 8 a 10. En la Tabla 7 se muestran los desplazamientos máximos obtenidos por el modelo simplificado y los distintos módulos de Young equivalentes considerados, junto al resultado obtenido por el MEF. En la Tabla 8 se muestra la diferencia porcentual de los resultados del modelo simplificado con respecto a los obtenidos por el MEF.
En las Figuras 8, 9 y 10 se puede observar que para el modelo simplificado, para los casos de material de pequeño espesor y sólido semiinfinito corregido, los resultados poseen una buena aproximación a los obtenidos por el MEF. En el caso del módulo elástico equivalente de Winkler se observa que el desplazamiento está muy sobreestimado. Esto se ve con mayor claridad en la Tabla 8 donde, para el material de pequeño espesor el error aproximado es de 5 % por defecto respecto a lo estimado por el MEF, para el material semiinfinito corregido el error es cercano al 15 %, también por defecto, mientras que para el módulo elástico de Winkler, los valores de desplazamiento se sobreestiman con un error muy elevado, que supera el 70 %.
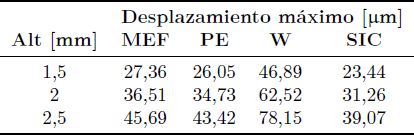
Tabla 7. Desplazamiento máximo obtenido por MEF y para el modelo simplificado de articulación de cadera natural con cada módulo elástico equivalente considerado
Figura 8. Superficies de desplazamiento obtenidas para cada módulo de Young equivalente y la correspondiente al MEF, para articulación natural sana. Alt = 1,5 mm. E = 10 MPa.
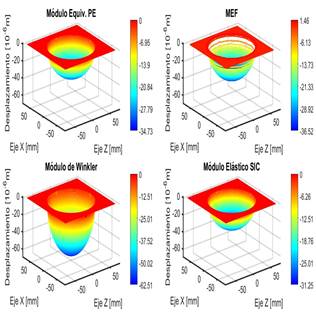
Figura 9. Superficies de desplazamiento obtenidas para cada módulo de Young equivalente y la correspondiente al MEF, para articulación natural sana. Alt = 2 mm. E = 10 MPa.
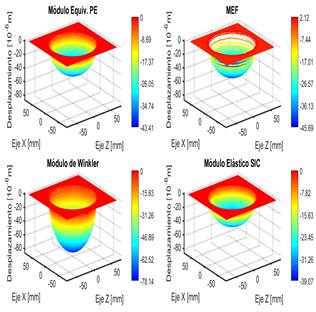
Figura 10. Superficies de desplazamiento obtenidas para cada módulo de Young equivalente y la correspondiente al MEF, para articulación natural sana. Alt = 2.5 mm. E = 10 MPa.
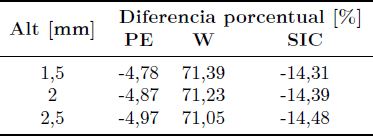
Tabla 8. Diferencia porcentual de los resultados PE, W y SIC respecto al obtenido por MEF para articulación de cadera natural
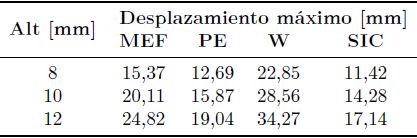
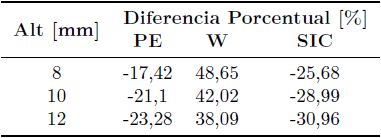
Tabla 9. Desplazamiento máximo obtenido por MEF y para cada módulo elástico equivalente considerado para el caso de articulación protésica
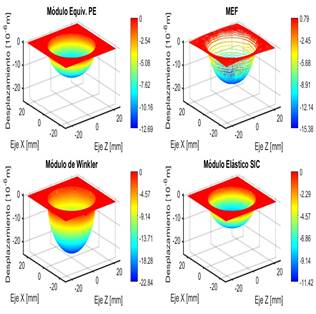
Figura 11. Superficies de desplazamiento obtenidas para cada módulo de Young equivalente y la correspondiente al MEF, para articulación protésica. Alt = 8 mm. E = 1 GPa
Figura 12. Superficies de desplazamiento obtenidas para cada módulo de Young equivalente y la correspondiente al MEF, para articulación protésica. Alt = 10 mm. E = 1 GPa.
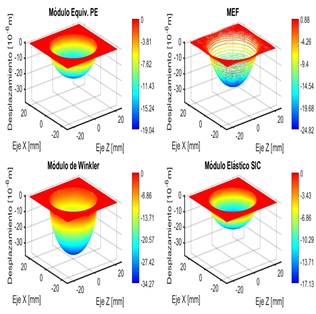
Figura 13. Superficies de desplazamiento obtenidas para cada módulo de Young equivalente y la correspondiente al MEF, para articulación protésica. Alt =12 mm. E = 1 GPa.
En las Figuras 11 a 13 se presentan los resultados correspondientes a prótesis de cadera. En este caso también son válidas las discusiones para la articulación sana de cadera, con la salvedad que las relaciones de diferencia o error porcentual son distintas. Comparando los desplazamientos máximos que se producen en el centro del contacto, se observa que para el material de pequeño espesor y el semiinfinito corregido los resultados del modelo simplificado difieren alrededor de un 20 y 30 %, respectivamente, por defecto respecto a lo obtenido por el MEF. Para el módulo elástico equivalente de Winkler, por su parte, se presenta un error del 38 y el 48 % en (Tabla 10). Ello se debe a que con el incremento del espesor del sólido, se mejora la aproximación de sólido semiinfinito, a la vez que empeora la aproximación SIC y la de pequeño espesor. Además, la aproximación PE, como en el caso de la rodilla, empeora por el aumento del módulo elástico entre el cartílago natural y el UHMWPE de la articulación protésica.
Conclusiones
Se ha presentado un análisis de deformaciones a partir del cálculo de desplazamientos de las superficies de dos sólidos en contacto cargado, para evaluar la pertinencia de utilizar modelos simplificados al momento de construir modelos de contacto. El estudio se motivó en las articulaciones humanas, donde el desplazamiento de las superficies en contacto es fundamental para posibilitar un flujo de lubricación que actúe minimizando el desgaste.
Para la predicción de los desplazamientos, se evaluaron tres módulos de Young equivalentes en un modelo simplificado de columna: para un sólido de pequeño espesor, para un sólido semiinfinito o de Winkler y para un sólido semiinfinito corregido.
Los resultados obtenidos para el módulo de Young equivalente correspondiente a un material de pequeño espesor, son los que mejor se aproximan a los obtenidos por el MEF en ambas geometrías consideradas: la del contacto lineal (equivalente a la rodilla) y la del contacto puntual (equivalente a la cadera). No obstante, las diferencias porcentuales respecto a la solución por MEF varían en cada caso y para cada material analizado: cartílago natural (menor al 5 % en cadera y menor al 1 % en rodilla) o UHMWPE en la articulación protésica (menor al 23,3 % en cadera y menor al 15 % en rodilla). Dichas diferencias en todos los casos son por defecto, lo cual no sería un problema en sí mismo ya que la subestimación pone al análisis del lado de la seguridad.
Quedó demostrado que los módulos de Young equivalentes derivados de la aproximación de sólido semiinfinito como el módulo de Winkler y el módulo de SIC, son inapropiados debido a la excesiva sobreestimación de los desplazamientos calculados obtenida al considerar el primero (mayor al 38 % y alcanzando el 70 % en varios casos) y la subestimación de los desplazamientos al considerar el segundo (superior al 10 % y alcanzando el 30 % en algunos casos), Ello, en virtud de lo dicho en el párrafo anterior, pone al análisis en riesgo para el caso de Winkler ya que, en modelos completos de lubricación, podrían predecirse separaciones entre las superficies en contacto mayores a las que en realidad se producirían.
Finalmente, el trabajo fue muy útil para el entrenamiento en las artes de la Mecánica Computacional de un alumno avanzado de la carrera de Bioingeniería, en su papel de becario de iniciación a la investigación de la Universidad Nacional de Entre Ríos, Argentina.
