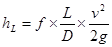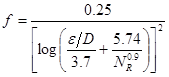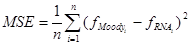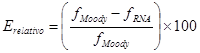Introducción
El método más utilizado para transportar fluidos de un lugar a otro es impulsarlo a través de un sistema de tuberías, siendo las de sección circular las más comunes para tal propósito, proporcionando mayor resistencia estructural y una mayor sección transversal para el mismo perímetro exterior que cualquier otra forma [1].
El flujo de un fluido en una tubería viene acompañado de una pérdida de carga que se contabiliza en términos de energía por unidad de peso del fluido que circula por ella [2].
Las pérdidas primarias o pérdidas de carga en un conducto rectilíneo de sección constante son debidas a la fricción del fluido contra sí mismo y contra las paredes de la tubería que lo contiene. Por otro lado, las pérdidas secundarias son pérdidas de carga ocasionadas por elementos que modifican la dirección y velocidad del fluido. Para ambos tipos de pérdida, parte de la energía del sistema se convierte en energía térmica (calor), que se disipa a través de las paredes de la tubería y de dispositivos tales como válvulas y acoplamientos [2–3].
La estimación de las pérdidas de carga debidas a la fricción en tuberías es una tarea importante en la solución de muchos problemas prácticos en las diferentes ramas de la ingeniería; el diseño hidráulico y el análisis de los sistemas de distribución de agua son dos ejemplos claros.
En el cálculo de las pérdidas de carga en tuberías desempeña un papel discriminante que el régimen de corriente sea laminar o turbulento [3]. El régimen de flujo depende principalmente de la razón de fuerzas inerciales a fuerzas viscosas en el fluido, conocida como número de Reynolds ( NR ) [4]. Así, si el NR es menor a 2000 el flujo será laminar y si es mayor a 4000 será turbulento [2]. La mayoría de los flujos que se encuentran en la práctica son turbulentos [2], [3], [4], por tal razón la presente investigación se desarrolla en mencionado tipo de régimen de flujo.
La Ecuación 1 planteada por Darcy-Weisbach es válida para el cálculo de las pérdidas por fricción en régimen laminar y turbulento en tuberías circulares y no circulares [2–4].
Donde:
hL: pérdida de energía debido a la fricción (N.m/N)
f: factor de fricción
L: longitud de la corriente del flujo (m).
D: diámetro de la tubería (m).
v : velocidad promedio del flujo (m/s).
g : aceleración gravitacional (m/s²).
La Ecuación 2, relación implícita conocida como ecuación de Colebrook, es utilizada universalmente para el cálculo del factor de fricción en flujo turbulento [3–4]. Nótese que la misma tiene un enfoque iterativo.
Donde:
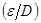 : rugosidad relativa. Representa la razón de la altura media de rugosidad de la tubería al diámetro de la tubería.
: rugosidad relativa. Representa la razón de la altura media de rugosidad de la tubería al diámetro de la tubería.
Una opción para el cálculo directo del factor de fricción en flujo turbulento es la Ecuación 3 desarrollada por K. Swamee y K. Jain [2].
Las ecuaciones (2) y (3), y otras tales como la de Nikuradse, Karman y Prandtl, Rouse, Haaland, son obtenidas experimentalmente y su uso puede resultar engorroso. Así, el diagrama de Moody es uno de los medios más empleados para determinar el factor de fricción en flujo turbulento [2–4]. Este muestra el factor de fricción como función del número de Reynolds y la rugosidad relativa. El uso del diagrama de Moody o de las ecuaciones antes mencionadas es un medio tradicional para determinar el valor del factor de fricción al resolver problemas con cálculos manuales. No obstante, esto puede resultar ineficiente. Para la automatización de los cálculos se requiere incorporar las ecuaciones en un programa u hoja de cálculo para obtener la solución.
El trabajo en cuestión presenta una propuesta alternativa para la predicción del factor de fricción empleando inteligencia artificial, concretamente una RNA que permite que el cálculo sea automático y fiable, reduciendo así tiempo y evitando errores que pueden ocasionarse al utilizar los medios citados previamente.
Materiales y métodos
Diseño de la RNA
La red multicapa a desarrollar tiene conexiones hacia adelante (feedforward) y emplea el algoritmo de retropropagación que es una generalización del algoritmo de mínimos cuadrados. Este trabaja mediante aprendizaje supervisado y, por tanto, necesita un conjunto de instrucciones de entrenamiento que le describa la respuesta que debería generar la red a partir de una entrada determinada [5].
Base de datos de la RNA
Los parámetros de inicialización de la RNA se obtienen de un conjunto de 724 datos tabulados en Microsoft Excel. Estos datos fueron adquiridos utilizando el diagrama de Moody, es decir, mediante el método gráfico que contempla una secuencia de pasos basados en [2]. El conjunto de datos considera 43 valores del Número de Reynolds, (4000 ≤ NR
≤ 1E8), 20 curvas de rugosidad relativa, (1E-6 ≤ 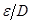 ≤ 0,05), y los respectivos factores de fricción.
≤ 0,05), y los respectivos factores de fricción.
Los números de Reynolds utilizados, expuestos en la Tabla 1, se corresponden con los marcados en la escala de las abscisas de la Figura 1, esto con la finalidad de lograr un cálculo exacto en el diagrama de Moody.
El número de Reynolds y la rugosidad relativa son las variables de entrada de la RNA y el factor de fricción es la variable de salida o variable a predecir. Con el propósito de establecer una adecuada base de datos se considera únicamente los factores de fricción que son consecuencia de una intersección evidente de cualquiera de los 43 Números de Reynolds en cada una de las curvas de rugosidad relativa.
Topología de la RNA
No se pueden dar reglas concretas para determinar el número de capas ocultas y el número de neuronas ocultas que debe tener una red para resolver un problema específico; el tamaño de las capas, tanto de entrada como de salida, suele estar determinado por la naturaleza de la aplicación [7–8]. Así, la problemática de la presente investigación sugiere que el número de Reynolds y la rugosidad relativa sean las dos entradas aplicadas en la primera capa y el factor de fricción, que es la salida, sea considera en la última capa de la red.
El número de neuronas ocultas interviene en la eficiencia de aprendizaje y de generalización de la red; además, en general una sola capa oculta suele ser suficiente para la convergencia de la solución, sin embargo, existen ocasiones en que un problema es más sencillo de resolver con más de una capa oculta [7–8].
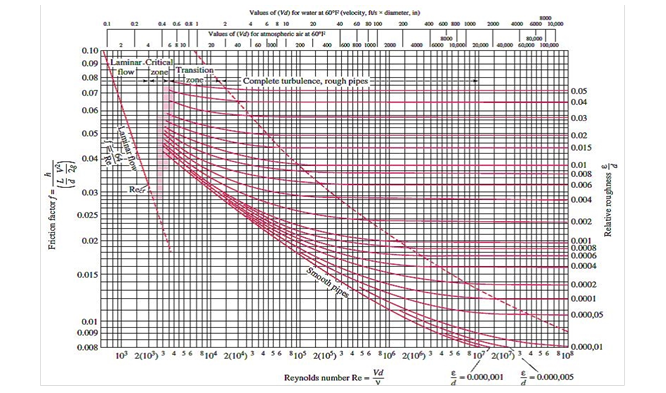
Figura 1. Diagrama de Moody para el coeficiente de fricción en conductos de paredes lisas y rugosas [6].
Por lo tanto, el número óptimo de capas y neuronas ocultas se determina a través de la experimentación.
Precisamente, se selecciona la topología más adecuada de la RNA ensayando diferentes configuraciones al variar el número de capas ocultas de una a tres y el número de neuronas dentro de cada capa oculta de 5 a 40 con incrementos de 5.
Entrenamiento de la RNA
El aprendizaje supervisado de una RNA implica la existencia de un entrenamiento controlado por un agente externo para que las entradas produzcan las salidas deseadas mediante el fortalecimiento de las conexiones. Una manera de llevar esto a cabo es a partir de la instauración de pesos sinápticos conocidos con anterioridad [5]. Por tal razón, el conjunto de pares entradas-salidas se aplica a la RNA, es decir, ejemplos de entradas y sus salidas correspondientes [5], [8], [9].
La red es entrenada con el algoritmo de retropropagación de Levenberg-Marquardt, pues es estable, fiable y facilita el entrenamiento de conjuntos de datos normalizados [10], [11], [12]. El entrenamiento es un proceso iterativo y el software, por defecto, divide el conjunto de 724 datos en 3 grupos: el 70 % comprende datos de entrenamiento, el 15 % datos de prueba y el 15 % restante los datos de validación. En cada iteración, al usar nuevos datos del conjunto de entrenamiento, el algoritmo de retropropagación permite que la salida generada de la red se compare con la salida deseada y se obtenga un error para cada una de las salidas. Al propagarse el error hacia atrás, desde la capa de salida hasta la capa de entrada, los pesos sinápticos de cada neurona se modifican para cada ejemplo, con el objeto de que la red converja hacia un estado que permita clasificar exitosamente todos los patrones de entrenamiento [9]. Esto conlleva a decir que el aprendizaje de la RNA se efectúa por corrección de error. A medida que se entrena la red, esta aprende a identificar distintas características del conjunto de entradas, de tal forma que cuando se le presente, luego del entrenamiento, un patrón arbitrario posea la capacidad de generalización, entendida como la facilidad de dar salidas satisfactorias a entradas no presentadas en la fase de entrenamiento [13].
Debido a la naturaleza de los datos de entrada y salida de la red multicapa, las funciones de activación o transferencia deben ser continuas, pudiendo, incluso, ser distintas para cada capa, siempre y cuando sean diferenciables [9–13]. Así, se aplica la función de activación tansig en las capas ocultas y la función de activación purelin en la capa de salida. Estas funciones son comúnmente usadas al trabajar con el algoritmo de retropropagación.
El aprendizaje de la RNA se detiene cuando el índice de error resulta aceptablemente pequeño para cada uno de los patrones aprendidos o cuando el número máximo de iteraciones del proceso ha sido alcanzado [10], [14], [15]. La función de rendimiento utilizada para entrenar la RNA es el error cuadrático medio (MSE), denotado por la Ecuación 4 [10–12]. El error relativo, reflejado aritméticamente por la Ecuación 5, es involucrado en el análisis [10–16].
Resumiendo lo expuesto, la Tabla 2 contiene las características de diseño de la RNA aplicadas a las distintas topologías ensaya
Resultados y discusión
Selección de arquitectura de la RNA
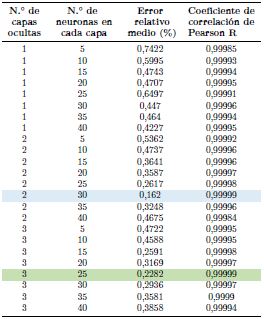
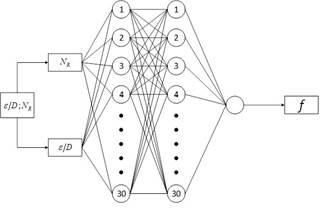
De acuerdo con la metodología planteada se entrenan un total de 24 arquitecturas, cuyos resultados se exhiben en la Tabla 3. Se observa que las topologías 2-30-30-1 y 2-25-25-25-1 presentan mejores resultados, pues poseen un error relativo medio de 0,1620 % y 0,2282 %, respectivamente, y un coeficiente de correlación de Pearson de 0,99999 para ambos casos. Sin embargo, se selecciona la primera de ellas debido a que manifiesta un menor error relativo medio de los valores pronosticados respecto a los deseados y demanda menor gasto computacional. Un esquema de la estructura de la RNA seleccionada se exhibe en la Figura 2. En ella se muestra las dos entradas externas, número de Reynolds y rugosidad relativa, aplicadas a la primera capa, las 2 capas ocultas con 30 neuronas cada una y en la última capa una neurona, cuya salida es el factor de fricción. Las entradas se limitan únicamente al flujo de información mientras que en las capas ocultas y de salida se realiza el procesamiento [5].
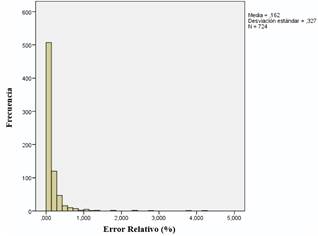
Mediante el software IBM SPSS Statistics 22® se realiza un análisis descriptivo de la variable error relativo para los 724 datos de la arquitectura seleccionada. El histograma de la Figura 3 representa las distribuciones de frecuencias. Se obtiene que la media es 0,1620 %, el error relativo mínimo es de 0 % y el máximo es de 4,2590 %.
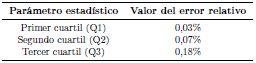
Además, la desviación estándar es de 0,327, indicando que la dispersión de los datos respecto a la media es pequeña. La distribución de datos manifiesta que existe un predominio considerable de error relativo menor al 1 % en el 97 % del total de datos analizados. Sustentando lo reflejado en el histograma, en la Tabla 4 se sintetizan los valores de los tres cuartiles obtenidos del análisis estadístico. Por debajo del Q1 existen errores relativos entre la salida deseada y la salida de la red menores al 0,0313 %. El Q2 , que es el valor de la mediana, señala que la mitad de los errores relativos están por debajo de 0,0720 %. El Q3 afirma que las tres cuartas partes de los datos tienen un error relativo menor al 0,1758 %. A partir del se obtienen errores relativos bajos, sin embargo, existen valores rezagados que son mayores al 1 %, pero estos representan solo el 3 % del total de datos analizados. Lo expuesto demuestra la calidad de aproximación de los valores pronosticados de la RNA respecto a los del diagrama de Moody.
Rendimiento del modelo
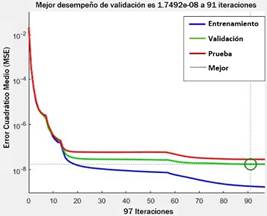
El rendimiento de los conjuntos de datos de entrenamiento, pruebas y validación en comparación con la salida deseada es mostrado en la Figura 4. La muestra destinada a la validación es usada para medir el grado de generalización de la red, deteniendo el entrenamiento cuando este ya no mejora, esto evita el sobreajuste (overfitting) [12], entendido como un pobre rendimiento del modelo para predecir nuevos valores. Se constata que el proceso de entrenamiento de la RNA con topología 2-30-30-1 es truncado en 91 iteraciones, pues es cuando se obtiene el menor valor MSE de validación que es de 1,7492E-8.
Es decir, se ha minimizado la función de rendimiento al máximo y ya no tendrá tendencia a disminuir pasadas las 91 iteraciones. Debido a que el valor MSE es muy pequeño, lo más cercano a cero, el modelo de RNA es capaz de generalizar con gran precisión.
En la Figura 5 se exhiben los resultados del coeficiente de correlación de Pearson R para la estructura de RNA diseñada. La línea indica los valores esperados y los círculos negros representan los valores pronosticados. La predicción es eficiente y se constata un buen desempeño de la red, pues se obtiene un índice global de 0,99999 que indica una relación lineal fuerte y positiva entre los factores de fricción del diagrama de Moody y los otorgados por la RNA.
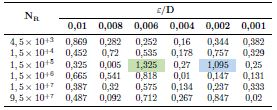
Se realizan varias pruebas con combinaciones de pares de entrada que no han sido utilizados durante el entrenamiento con el objeto de verificar el correcto desempeño del modelo. Así, en la Tabla 5 se detallan las 36 combinaciones de datos de entrada aplicados a la RNA y el error relativo alcanzado por cada una de ellas.
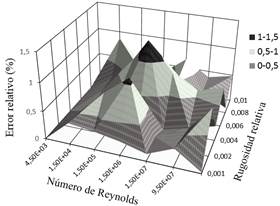
De acuerdo con la Tabla 5 y la Figura 6, el error relativo no se distribuye por igual en el rango de los valores de entrada. En el gráfico de superficie 3D generado se observa el predominio de un error relativo menor al 0,5 %, correspondiente a 24 de las 36 combinaciones de pares de entrada aplicadas a la RNA. Además, únicamente existen 2 errores relativos por encima del 1 %, concernientes a los 2 picos más prominentes de la superficie, siendo el máximo de 1,325 % para N R = 1,5E5 y E/D = 0,006. Los resultados derivados de estas 32 pruebas corroboran el correcto funcionamiento de la red y su capacidad de generalización al presentarle entradas distintas a las utilizadas en la fase de entrenamiento.
Conclusiones
La RNA diseñada en esta investigación representa una alternativa fiable y de gran precisión para predecir el coeficiente de pérdidas primarias en régimen de flujo turbulento, dando un error relativo medio de 0,1620 % y un coeficiente de correlación de Pearson R de 0,99999 entre los valores del diagrama de Moody y los pronosticados.
El proceso de entrenamiento se detuvo en 91 iteraciones, alcanzando un MSE de 1,7492E-8 que indica la capacidad de generalización de la RNA propuesta.
Los resultados obtenidos demuestran que el conjunto de 724 datos fue suficientemente grande para permitir que la RNA, durante el entrenamiento, sea capaz de aprender la relación entre las entradas y salidas aplicadas.
El modelo desarrollado permite resolver problemas de flujo que involucran cálculos del factor de fricción de una manera automática, aprovechando la rapidez computacional que ofrecen las redes neuronales, reduciendo así tiempo y evitando errores que pueden ocasionarse al utilizar los medios tradicionales para tal efecto.