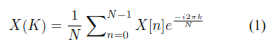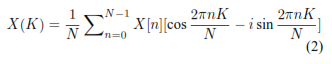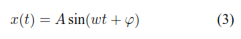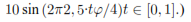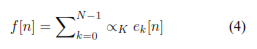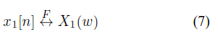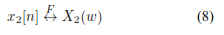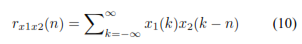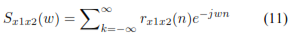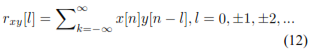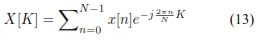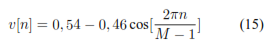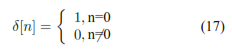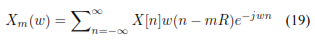Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
uBio 
Permalink
1. Introducción
La reconstrucción de señales a partir de la información parcial en el dominio de la frecuencia, para varios autores es interesante en diferentes campos de la investigación, como es el desarrollo de condiciones aplicadas a las señales, en las que se especifican de manera única mediante la información de magnitud o fase, por lo que, se han desarrollado algoritmos computacionales prácticos para recuperar las señales a partir de esta información [1, 2]
En este trabajo, se considera el problema de reconstruir señales a partir de la información en frecuencia utilizando la transformada discreta de Fourier (DFT) o la transformada inversa de Fourier discreta (IDFT). Por tanto, la herramienta DFT convierte datos muestreados en el dominio del tiempo en datos muestreados en el dominio de la frecuencia y viceversa. Sin embargo, la transformada rápida de Fourier (FFT) es una implementación eficiente de la DFT, utilizada en el campo de las comunicaciones, específicamente en el filtrado de dominio de frecuencia y aplicaciones para el procesamiento de señales de video y audio [3]. El presente trabajo solo se enfoca en el análisis de la DFT.
La DFT es una técnica muy conocida para el procesamiento digital de señales (DSP), por ejemplo, es utilizada para determinar la distribución de frecuencias de una señal finita muestreada con espacios iguales. Además, la DFT tiene un papel importante en muchas aplicaciones inalámbricas y la transformación de una señal al dominio de la frecuencia, suele ser un paso necesario para el procesamiento posterior o para la extracción de información [4].
Las aplicaciones de la DFT en el campo del análisis espectral digital tienen, por ejemplo, analizadores de espectro, procesamiento de voz e imagen, eliminación de ruido, y reconocimiento de patrones.
En el campo de las DSPs, se tiene una señal que varía en el tiempo, como una señal de radio, la presión de una onda de sonido o lecturas diarias de temperatura, las cuales son muestreadas en un intervalo de tiempo finito (generalmente definido por una función de ventana).
En el caso del procesamiento de imágenes, las muestras pueden ser los valores de píxeles a lo largo de una fila o columna de una imagen de trama [5].
La DFT puede ser convertida en funciones seno y coseno o A+iB. La señal discreta x[n] tiene un periodo N y se puede convertir en una señal discreta en el dominio de la frecuencia de longitud N. La relación entre las muestras de entrada mediante senos y cosenos, se obtiene la señal DFT compleja que viene dada por la ecuación 1 y 2 [3].
Donde 0 ≤ k ≤ N − 1.
La siguiente sección refiere sobre la descripción general de la DFT considerando conceptos básicos, ecuaciones y su enfoque hacia el procesamiento espectral en frecuencia, la sección dos trata sobre los algoritmos que se pueden utilizar para la solución de problemas basados en la DFT, considerando su bajo costo computacional. Finalmente, se presentan las conclusiones del estudio.
1.1. Definiciones para la DFT
1.1.1. Señales
Las señales son cualquier función real o compleja de la variable de tiempo t. Por otro lado, una señal se puede describir como una función de un solo valor de una o más variables independientes. Ejemplo de una señal: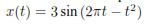 
donde 
, Figura 1
1.1.2. Sinusoide
Una sinusoide es una función que tiene la forma de la ecuación 3.
Donde t es la variable independiente y los parámetros fijos A,ω,𝜑 son constantes. En una aplicación de audio se tiene típicamente, A que representa la amplitud, w la frecuencia en rad/s o también igual a 2πf donde f es la frecuencia en Hertz (Hz) y φ es la fase inicial. La Figura 2 muestra un ejemplo de sinusoide para A = 10; f =
.
También se puede manejar señales coseno que no es más que una sinusoide en fase π/2, mientras que la sinusoide está en fase 0, entonces el concepto de señales sinusoidales es igual a funciones seno o coseno con alguna amplitud, frecuencia y fase definida.
Las sinusoides surgen naturalmente de diferentes formas de ahí su importancia ya que son fundamentales en sistemas físicos que son oscilantes y resonantes como movimientos armónicos y sobre todo su importancia en sistemas lineales que permite el análisis de filtros señales como se revisará más adelante.
1.1.3. Señales discretas
Una señal de tiempo discreto es una secuencia de valores de interés, donde el índice entero se puede considerar como un índice de tiempo y los valores de la secuencia representan alguna cantidad física de interés. Una señal de tiempo discreto es una secuencia x[n] definida para todos los enteros n.
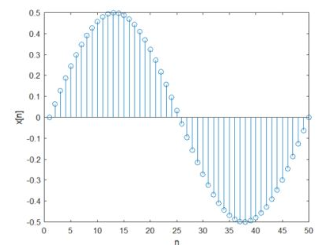
En la Figura 3 se tiene la gráfica de la señal discreta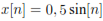 
.
1.1.4. Tasa de muestreo
La tasa de muestreo permite digitalizar una señal analógica que puede ser de sonido y representarla por un flujo de números; cada muestra se puede considerar como un número que especifica la posición de un altavoz en un instante particular. Cuando el sonido ha sido muestreado se le llama audio digital.
Una tasa de muestreo de 44,1 kHz se usa comúnmente para la reproducción de música esto quiere decir que el altavoz se está moviendo a una nueva posición 44.100 veces por segundo o una vez cada 23 microsegundos.
Ahora la cuestión es cómo se puede seleccionar una tasa de muestreo adecuada para una señal, al igual que el ejemplo del sonido se debe disponer de alguna información sobre las características de la señal que se va a muestrear [6]. En concreto, se necesita conocer información general acerca del contenido en frecuencia de la señal. Normalmente, dicha información estará disponible. Otro ejemplo sería que las principales componentes de frecuencia de una señal de voz se encuentran por debajo de los 3.000 Hz. Por otro lado, las señales de televisión, generalmente, contienen componentes de frecuencia importantes hasta los 5 MHz.
La información implícita en las señales se encuentra en parámetros de amplitudes, frecuencias y fases de las diversas componentes de frecuencia, se debe tener en cuenta que la información de las características de las señales no será visible hasta poder obtener dichas señales. Por ende, el objetivo de DSP es extraer dicha información de manera minuciosa. Es importante manifestar que si se conoce la frecuencia máxima de la señal se podrá especificar la frecuencia de muestreo necesaria para convertir las señales analógicas en señales digitales lo que se conoce como el teorema de muestreo.
Este teorema indica que la frecuencia más alta de una señal analógica que puede reconstruirse sin errores o ambigüedades cuando se muestrea la señal a una frecuencia Fs = 1/T es Fs/2. Cualquier frecuencia por encima de F s/2 o por debajo de - Fs/2 produce muestras que son idénticas a las correspondientes frecuencias dentro del rango -Fs/2≤F ≤Fs/2. Para evitar estas ambigüedades o problemas de aliasing se debe elegir una frecuencia de muestreo que sea suficientemente alta de modo que Fs≥2Fmax [6].
1.1.5. Series de Fourier discretas
Para la secuencia dada f[n] con periodicidad N, se tiene que ƒ[n+N ] = ƒ[n], entonces la expansión de Fourier de f [n] está dada por la ecuación 4 [6].
Donde las funciones de base de Fourier son la ecuación 5 y la ecuación 6 referida a los coeficientes de Fourier:
1.1.6. Teorema de correlación
Si se tiene las señales x1[n] y x2[n] de las que se puede obtener su respuesta en frecuencia de tal forma que:
Entonces al aplicar la transformada de Fourier
Y aplicando la convolución se tiene la ecuación 10.
Si se multiplica ambos lados de la ecuación 10 por la exponencial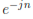 
y sumando para todo n se obtiene la ecuación 11.
La ecuación 8 se conoce como densidad de energía cruzada de las señales x1[n] y x2[n]
1.1.7. Correlación cruzada
La correlación cruzada de dos señales reales x[n] e y[n] es una secuencia r x y[l], la cual se define como en la ecuación 12.
El índice l es el parámetro de desplazamiento de tiempo y el subíndice xy empleado en la secuencia de correlación cruzada r xy [l] indica las secuencias que se van a correlacionar. El orden de los subíndices, cuando x precede a y, indica la dirección en que se desplaza una secuencia respecto a la otra. En concreto, en la ecuación 10, la secuencia x[n] no se desplaza e y[n] se desplaza l unidades de tiempo hacia la derecha para l positivo y hacia la izquierda si l es negativo [6].
1.2. Descripción general de la transformada discreta de Fourier
Considerando el muestreo de la transformada de Fourier de una secuencia periódica de tiempo discreto, se ha establecido una relación entre la transformada de Fourier muestreada y la DFT. Cuando una señal es periódica en el dominio del tiempo, es posible utilizar la representación de series de Fourier en tiempo discreto (DTFS). Entonces, el espectro en el dominio de la frecuencia será discreto y periódico. Sin embargo, en el caso de representar una secuencia no periódica o de duración finita en el dominio de la frecuencia, es posible mediante la aplicación de esta propiedad de periodicidad de las representaciones DTFS. Por lo tanto, esto se considera como una DFT [6]. La DFT proporciona un método para transformar una secuencia dada a el dominio de la frecuencia y para representar el espectro de la secuencia usando solo valores k de frecuencia, donde k es un número entero que toma N valores, K = 0; 1; 2, ., N −1: Las ventajas de la DFT son [7]:
1.2.1. Transformada discreta de Fourier
Sea x[n] una señal de tiempo discreto con período N. Entonces, la DFT X[k] de x[n] es la señal en tiempo discreto definida por la ecuación 13:
Donde N es el tamaño de la DFT. La DFT X[k] de x[n] es una secuencia de números complejos. Entonces, x[n] es cero fuera de la ventana de datos de entrada n = 0, 1, …, N −1. Las muestras de la señal se pueden calcular a partir de los coeficientes DFT usando la siguiente ecuación 14.
Donde n = 0, 1, …, N −1. Aquí la ecuación 11 se conoce como la IDFT. En el dominio n ∈ [0,N-1] esta es la transformada inversa de la ecuación 10. En esta interpretación, cada X[k] es un número complejo que codifica tanto la amplitud como la fase de una componente sinusoidal 
de la función x[n]. La frecuencia de la sinusoide es k ciclos por N muestras.
1.2.2. La DFT en el filtrado lineal
Como la DFT proporciona una representación discreta en frecuencia de una secuencia de duración finita en el dominio de la frecuencia, es interesante explorar su uso como una herramienta de cálculo para el análisis de sistemas lineales y, especialmente, del filtrado lineal. Se analiza un procedimiento de cálculo que sirve como alternativa a la convolución en el dominio del tiempo. De hecho, el método en el dominio de la frecuencia basado en la DFT es más eficiente en lo que se refiere a los cálculos que la convolución en el dominio del tiempo, gracias a la existencia de algoritmos eficaces para calcular la DFT [8].
1.2.3. Transformada rápida de Fourier
La transformada de Fourier rápida (FFT) consiste en algunos métodos para calcular la DFT de manera eficiente debido a la importancia que tiene esta en las aplicaciones de tratamiento digital de señales como el filtrado, análisis de la correlación y análisis espectral. Uno de estos métodos consiste en la descomposición de una DFT de N puntos en transformadas DFT sucesivamente más pequeñas. Este método básico nos lleva a una familia de algoritmos de cálculo eficientes conocidos colectivamente como algoritmos FFT [7].
La ecuación 15 denota la función de ventana de Hamming la cual proporciona más suavizado a través de la operación de convolución en el dominio de la frecuencia.
1.2.4. Respuesta en frecuencia de las señales
Los sistemas se analizan en el dominio del tiempo usando convolución. Sin embargo, se puede hacer un análisis paralelo en el dominio de la frecuencia mediante el uso de la transformada de Fourier.
Cada señal de entrada se puede representar como un grupo de ondas coseno, cada una con una amplitud y un cambio de fase específicos. Por lo tanto, la DFT se puede utilizar para representar cada señal de salida de forma similar [9].
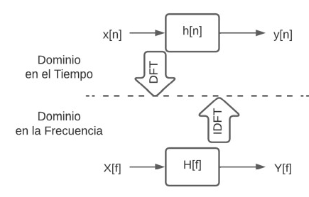
Cualquier sistema lineal puede describirse completamente por el comportamiento que cambia la amplitud y la fase de las ondas cosenoidales que lo atraviesan; esta información se conoce como la respuesta de frecuencia del sistema. Dado que tanto la respuesta de frecuencia como la respuesta de impulso contienen información completa sobre el sistema de señales, debe haber una correspondencia biunívoca entre las dos. La conexión entre la respuesta de frecuencia y la respuesta al impulso es una de las bases del procesamiento de señales. La respuesta de frecuencia de un sistema es la transformada de Fourier de su respuesta al impulso, que se ilustra en la Figura 4.
Considerando la notación DSP estándar, las variables en minúsculas se utilizan para representar las respuestas al impulso, mientras que las variables en mayúsculas se utilizan para representar las respuestas en frecuencia.
Dado H (f ) para la respuesta de frecuencia y h[n] para la respuesta de impulso. Los sistemas se describen en el dominio del tiempo por convolución, como: y[n] = x[n] * h[n].
En el dominio de la frecuencia, el espectro de entrada se multiplica por la respuesta de frecuencia, como: Y (f) = X(f )H(f ), lo que da como resultado el espectro de salida.
1.2.5. Ruido
Es el conjunto de señales que no son de interés y degradan o distorsionan la señal original, limitando el estudio de la información contenida en la señal original [10]. Considerando el análisis de espectro de a siguiente secuencia:
En ausencia de cualquier otra información, esto es una simple lista de números que puede ser la variación de temperatura de un día a otro en alguna localidad, o puede ser la normalización de muestras sucesivas de un sonido. No existe una forma de saber si esos números son randómicos o ya definidos. Lo mejor que se puede hacer es estimar la probabilidad de que estos números se generaron de acuerdo con alguna distribución normal, lo importante es que cualquier análisis de ruido de este tipo impone la suposición de que los datos de ruido fueron generados por algún proceso aleatorio.
Se debe tener en cuenta que el análisis se lleva a cabo en términos de algún modelo de señal subyacente que representa las suposiciones con respecto a la naturaleza de los datos.
Para identificación de sistemas FIR se considera el proceso estocástico estacionario que puede crearse pasando ruido blanco a través de un filtro lineal invariante en el tiempo [6].
1.2.6. Espectro
Se emplea el término espectro para hacer referencia al contenido en frecuencia de una señal [6].
La descomposición de la señal en sus componentes sinusoidales, las series de Fourier y la transformada de Fourier permiten realizar dicha descomposición, realizar nuevamente la combinación de las componentes sinusoidales para reconstruir la señal original es un problema de síntesis de Fourier. Este desarrollo es muy importante ya que permite llevar un adecuado análisis en el dominio de la frecuencia mediante una representación matemática y gráfica de las componentes de frecuencia contenidas en una determinada señal [11].
1.2.7. Respuesta al impulso de una señal
Cualquier filtro lineal o invariante en el tiempo (LTI) puede representarse en el dominio del tiempo por su respuesta a una señal específica denominada impulso, esta respuesta se llama naturalmente la respuesta de impulso del filtro [11]. Cualquier filtro LTI puede implementarse convolucionando la señal de entrada con la respuesta de impulso del filtro. La señal impulso es denotada δ[n] y definida por la ecuación 17.
La respuesta al impulso de un filtro es la respuesta del filtro a δ [n] y la mayoría de las veces es denotada como h[n] en la ecuación 18.
La respuesta al impulso h[n] es la respuesta del filtro L en el tiempo n para un impulso unitario ocurrido en el tiempo 0.
1.2.8. Ventana de Hamming
En la transformada de Fourier es importante la influencia de la longitud de la ventana, cuanto mayor es la ventana mayor es la resolución del dominio de frecuencia y disminuye la resolución de tiempo correspondiente, son utilizadas en el análisis y procesamiento de señales para también evitar discontinuidades al principio y al final de los bloques analizados.
La ventana de Hamming tiene una forma sinusoidal que resulta en un pico y lóbulos laterales bajos, esta ventana realiza un mejor trabajo de cancelar el lóbulo lateral más cercano, pero es más deficiente al cancelar cualquier otro [11].
1.2.9. Transformada de Fourier de tiempo corto
La transformada de Fourier de tiempo corto (STFT) es una poderosa herramienta de propósito general para el procesamiento de señales de audio. Define una clase particularmente útil de distribuciones de tiempo-frecuencia que especifican una amplitud compleja frente al tiempo y la frecuencia de cualquier señal. Aquí interesa principalmente, ajustar los parámetros STFT para: resolver los armónicos y seguir de cerca las variaciones de tono. La ecuación 19 representa la STFT [11].
Donde x[n] es la señal de entrada al tiempo n, (n) longitud M de la ventana de Hamming y R es el tamaño del salto en muestras. De esta forma se realiza un análisis localizado de la señal enventanada alrededor de la muestra n y analizada a todas las frecuencias.
Una vez que la ventana ha sido elegida para realizar la STFT, la resolución temporal y frecuencial es fija sobre todo el plano tiempo-frecuencia puesto que se utiliza la misma ventana para extraer las características espectrales a todas las frecuencias.
2. Materiales y métodos
2.1. Simulador numérico
Se utiliza una plataforma de programación y cálculo numérico que permite analizar datos, desarrollar algoritmos y crear modelos matemáticos. El sistema ofrece un entorno de desarrollo integrado con un lenguaje de programación propio que puede ejecutarse tanto en el entorno interactivo, como a través de un archivo de script, este lenguaje permite operaciones de vectores y matrices, funciones, cálculo y programación orientada a objetos. En esta plataforma también se puede añadir la creación de interfaces de usuario y la comunicación con otros lenguajes de programación e incluso con otros dispositivos. Además, permite el estudio de sistemas continuos, discretos, lineales y no lineales, mediante descripción interna y externa, en el dominio temporal y frecuencia, también es posible diseñar y analizar filtros FIR, IIR, multitasa, multietapa y adaptativos. Puede transmitir señales desde variables, archivos de datos y dispositivos de red para desarrollar y verificar sistemas.
2.2. Algoritmo de la DFT
Es indispensable tener en cuenta los elementos simultáneos que intervienen en el diseño y funcionamiento de la DFT por lo que como metodología para su desarrollo se utiliza un enfoque teórico práctico realizando previamente el estudio y comprensión de la transformada de una manera teórica para posteriormente de manera efectiva sintetizar esos conocimientos en la construcción del algoritmo. La DFT es un algoritmo simple que consiste en recorrer todos los puntos de datos digitalizados de la función de entrada, y multiplicar cada punto por funciones de seno y coseno, y sumando los productos resultantes en acumuladores (donde uno es para el componente seno y otro para el coseno). Cuando se ha procesado todos los puntos de datos, se divide el resultado de los acumuladores por el número de puntos de datos, obteniendo los valores promedio de los componentes del seno y el coseno en frecuencia. Se debe repetir este proceso para todas las frecuencias de múltiplos enteros, hasta que la frecuencia sea igual a la tasa de muestreo menos 1 (es decir, el doble de la frecuencia de Nyquist menos 1), concluyendo con el proceso [10].
Los ejemplos a continuación dan una progresión desde el análisis más simple hasta un tratamiento práctico adecuado, se lleva a cabo el análisis de espectro en datos reales aplicando la DFT [11].
3. Resultados y discusión
3.1. FFT de una simple sinusoide
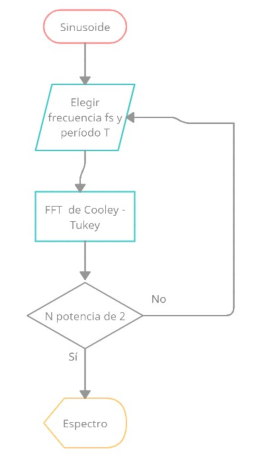
El primer ejemplo es una FFT de una simple sinusoide x[n] = cos(xnT ), donde x = 2(fs/4)(frecuencia fs/4Hz) y T = 1 (frecuencia de muestreo fs establecida en 1). Se usa una FFT de Cooley-Tukey, donde la longitud de la señal N debe ser una potencia de 2 para obtener los resultados más rápidos. Obteniendo la siguiente gráfica que se indica en la Figura 5:
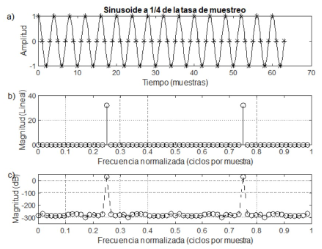
Fig. 5: Sinusoide muestreada a la frecuencia f = fs/4. a) Forma de onda en el tiempo. b) Espectro de magnitud. c) Espectro de magnitud DB.
Los resultados indicados en las gráficas de la Figura 5, se tiene que la señal en el dominio del tiempo se muestra en el gráfico superior (Figura 5.a), tanto en forma pseudocontinua como muestreada. En el gráfico central (Figura 5.b), se determinan dos picos en el espectro de magnitud, cada uno con una magnitud de 32 en una escala lineal, ubicados en frecuencias normalizadas f = 0; 25y f = 0,75. Una amplitud de pico espectral de 32 = (1/2)64, lo cual es un resultado valido, teniendo en consideración N. El espectro debe ser exactamente cero en sus picos. La precisión con la que esto sucede se puede ver en una escala de dB, como se muestra en la Figura 5.c. Resulta que la magnitud espectral en los otros contenedores es del orden de 300dB más bajo, que está lo suficientemente cerca de cero para un trabajo con audio. El diagrama del algoritmo empleado se puede apreciar a detalle en la Figura 6, en donde se observa la importancia de verificar la longitud de la señal como paso previo para aplicación de la FFT.
3.2. Identificación de un sistema FIR
La estimación de una respuesta al impulso a partir de mediciones de entrada-salida se denomina identificación del sistema [12].
La correlación cruzada se puede utilizar para calcular la respuesta al impulso h(n) de un filtro a partir de la correlación cruzada de sus señales de entrada y salida x(n) y y = h * x respectivamente según el teorema de correlación: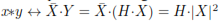 
. Por lo tanto, la respuesta en frecuencia es igual al espectro cruzado de entrada-salida dividido por el espectro de potencia de entrada: 
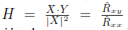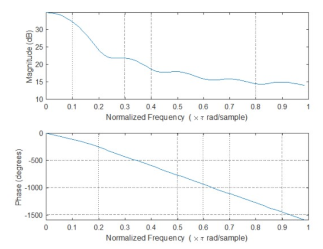
donde la multiplicación y división de espectros se definen por puntos, es decir, 
. Se presenta los resultados en frecuencia normalizada en la gráfica de la Figura 7.
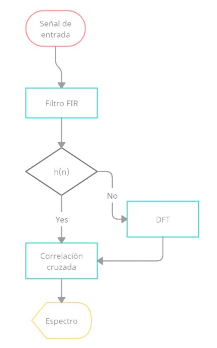
Además, se muestra el diagrama del algoritmo implementado en la Figura 8, en donde se indica el proceso completo para obtener la respuesta de frecuencia, se debe notar la intervención de la DFT en el análisis FIR.
3.3. Espectrograma
El espectrograma es una herramienta básica en el análisis espectral de audio y otros campos. Se ha aplicado ampliamente en el análisis de la voz, se puede definir como un gráfico de intensidad (generalmente en una escala logarítmica, como dB) de la magnitud de la transformada de Fourier de tiempo corto (STFT). Es una representación importante de los datos de audio porque la audición humana se basa en una especie de espectrograma en tiempo real codificado por la cóclea del oído interno. El espectrograma se ha utilizado ampliamente en el campo de la música por computadora como guía durante el desarrollo de algoritmos de síntesis de sonido [13].
Se realiza el espectrograma de una grabación de audio la cual ha sido generada mediante un algoritmo, dicho espectrograma es computado como una secuencia de FFT´s en una ventana de Hamming cuya longitud se toma de 20ms que típicamente contiene los datos de un fonema.
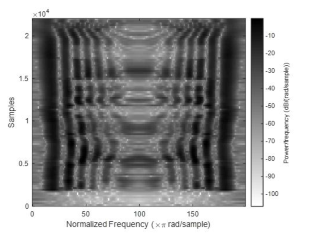
El espectrograma obtenido se pude observar en la Figura 9, la ventana permite incluir al menos dos períodos de la frecuencia fundamental durante la muestra de voz suponiendo que el tono más bajo sea de alrededor de 100 Hz.
Las componentes en el habla son las resonancias en el tracto vocal estas aparecen como un grupo oscuro de armónicos en la Figura 9, estas componentes determinan en gran medida la vocal en el habla que comparada con el habla telefónica se encuentra nominalmente entre 200 y 3.200 Hz. Se debe tener en cuenta también el tamaño de la ventana utilizada con la STFT que incide al momento de realizar una buena estimación de la frecuencia instantánea a través de la convolución.
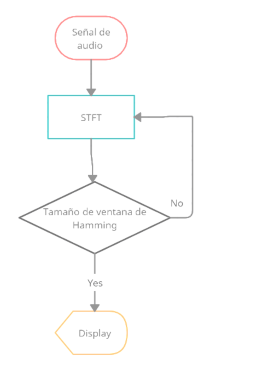
Se puede apreciar el diagrama del algoritmo implementado en la Figura 10 en donde se nota la condición importante de verificar el tamaño adecuado de la ventana de Hamming para la aplicación de la STFT.
4. Conclusiones
El desarrollo del primer ejemplo demuestra el uso de la DFT en una sinusoide simple en el que se puede elegir parámetros de la señal y el uso de la FFT para obtener gráficas detalladas de la magnitud del espectro de una sinusoide de forma lineal o en dB lo que permite un análisis minucioso del espectro de la señal.
En el segundo ejercicio, para la estimación de la respuesta al impulso de un sistema es necesario acudir a una operación muy importante de la DFT como lo es la correlación cruzada para la obtención de una gráfica que permite analizar la respuesta en una frecuencia normalizada, tanto en magnitud como en fase. Esta implementación resulta una poderosa herramienta de filtros FIR para el procesamiento digital de señales.
En el uso de la DFT en la obtención de un espectrograma mediante la STFT, se debe tener especial atención en el tamaño de la ventana de Hamming utilizado, misma que permite controlar el ancho de banda del lóbulo principal y el decaimiento de los lóbulos laterales, esto permite analizar las señales de manera que se puedan detectar las frecuencias que componen dicha señal extrayendo la información necesaria.
