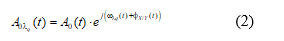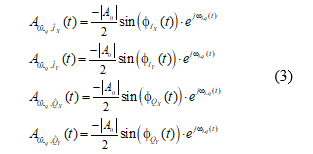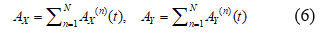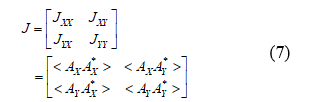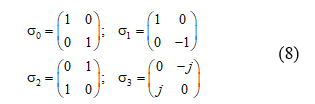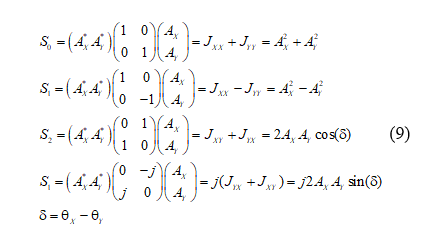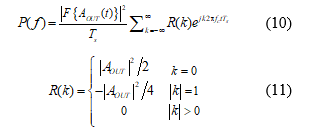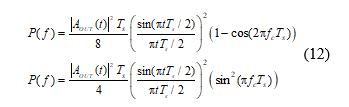Introduction
In recent years, network operators have been considering and installing network infrastructures even more robust than those before them. The rapidly increasing demand for transmission capacity and the ineffective use of optical fiber links have led to many studies to develop advanced schemes that achieve transmission rate beyond 240 Gb/s per wavelength channel.
A promising approach to improving the transmission performance of future access networks, called multidimensional modulations was discovered a long time ago by Wei 1. This technique involves the use of a rectangular or cross-lattice grouping technique to provide other modulations formats, being compatibility with traditional formats. This strategy improves the peak-to-average power ratio (PAPR) and SNR efficiency due to shaping component constellation-expansion-ratio (CER) that depends only on the shape of the constellation. Consequently, the shape gain (dB) is evaluated in terms of PAPR and CER, where cross constellations achieve better results in comparison with rectangular constellations.
The increase in PAPR is considered primarily as a negative effect of OFDM systems. However, this technique has more recently been applied to modern mobile access networks, such as sparse code multiple access networks (SCMA) 2 to achieve the high capacity needed to support large volumes of information and massive connectivity.
It is widely known, that optical-fiber communication is a strong candidate for connecting the backbone with the end-users in future access networks. For this reason, research has been done to optimize optical channels by using advanced modulation formats so that they can transmit data at higher rates with flexible spectral and power efficiency. Furthermore, N-dimensional signal constellations may be incorporated to increase the system performance compared to that using traditional two-dimensional (2D) formats.
In this context, the spectrum allocation in conventional WDM Network is replaced for an elastic optical network (EON) which improves the spectral efficiency. EON is based on OFDM, they provide an alternative to single carrier modulation technique as the data stream divided and multiplexed onto multiple consecutive low rate subcarriers and hence increases the symbol duration and provides a higher data rate 3. This approach leads us to think that our proposal is the key to the next generation of optical networks in order to obtain a flexible allocation of spectral resources improving in this way the spectral efficiency.
Incoherent detected optical transmission, polarization-division-multiplexing (POLMUX) can be used to generate two orthogonal polarization signals, X and Y, for transmission through a single-wavelength channel with a high SE and ultra-high-speed 4. In this context, passive optical networks with two orthogonally polarized orthogonal frequency-division multiple access signals have recently been proposed. This system can transmit data at a rate of 108 Gb/s after 20km SSMF in comparison with the back-to-back transmission. The fiber dispersion penalty is negligible due to distance of transmission, the attenuation (15dB) and the excellent Bit Error Rate (BER) achieved 1.4×10-3 (5.
Adaptive turbo-trellis-coded modulation (ATTCM32QAM) provides 7.3dB (BER = 1×10-3) coding gain 6 compared to uncoded system (16QAM) that achieves and 2.3dB (BER = 1×10-3) coding gain.
In this way, wavelength-division multiplexing (WDM) can facilitate the integration of coding (FEC, trellis, turbo code, LDPC) with code modulation together in order to improve the spectrum efficiency and coding gain. These are the promising solutions for 5G network access with optical communications known as 10-Gigabit-capable passive optical networks (XG-PON) 7 that should coexist with GPON and WDM-PON networks, and also guaranteeing an optimal allocation of wavelength bands in order to avoid the undesirable interference of GPON with XG-PON.
Another promising technology is the polarization switching system, which sends a three-dimensional (3D) constellation with an asynchronous in-phase/quadrature (IQ) polarization, which represents the transmitted symbol in 3D 8. Dual-polarization (DP) modulation provides a lower SE but better performance for a long-distance transmission 9.
4D set-partitioning quadrature amplitude modulation (SP-QAM) is a special case of advanced optical modulation, in which a regular 4D cubic can be constructed by polarization-division multiplexing (PDM). A PDM-QAM model using a coherent detection scheme with Reed-Solomon encoding was shown to improve the SE and provide a data transmission rate of over 112 Gb/s 10. In another study, the use of 4D 512-ary and 2048-ary SP-QAM signals and soft-decision forward error correction (FEC) with penalties resulted in BERs of 3.8×10-3 and 2×10-2, respectively 11.
In addition to the use of spectrally efficient modulation formats low-density parity-check (LDPC) codes can be incorporated into the physical design for new schemes to make them compatible with 4D modulations and, thereby, enable coherent optical communications with high aggregate bit rates. LDPC codes offer significant benefits compared to other codes and hybrid codes like turbo-trellis code modulations. In this context, 4D bit-interleaved LDPC-coded modulation has been developed by connecting a distributed-feedback (DFB) laser to a polarization beam splitter (PBS) to combine two polarization (X and Y) for each IQ modulator, thus, forming the structure of a 4D modulator 12. The aggregate information bit rates with 16-, 32-, and 64-QAM were measured as 160, 200, and 240 Gb/s, respectively; the best optical SNR of approximately 5 dB and a BER of 1×10-8 was attained with 16-QAM. In another study, 320 Gb/s data transmission was achieved using an M-ary 3D constellation with LDPC coded modulation; an SNR of nearly 12dB and a BER of 1×10-9 was achieved for 8-QAM 8.
Therefore, the optimization of the power efficiency of an N-dimensional constellation that provides both flexible SE and high-power efficiency at the same time can be solved by considering it as a sphere-packing problem 13. The number of degrees of freedom for optical transmission can be represented by the vertical axis, where the first and second dimensions represent the electrical field of the X-polarized IQ components, and the third and fourth dimensions represent the electrical field electrical of the Y-polarized IQ components. In this context, a 4D lattice is constructed, and optimized with respect to the discrete-time represented by the horizontal axis. This approach has been used to optimize a 3D constellation with four degrees of freedom, achieving data transmission of 224 Gb/s over a distance of 100km.
The use of polarization-mode dispersion can improve the coding gain due to the error floor and the iterative exchange of extrinsic soft-bit reliabilities between posterior probabilities. Hussam developed a way to implement such a modulation with different sub-carriers in a 3D space using coded hybrid sub-carrier/amplitude/phase/polarization (H-SAPP) 14. Using Stokes parameters, H-SAPP allows 20 points to be incorporated into a 3D constellation mapping in the form of a dodecahedron inscribed in a Poincaré sphere based on regular polyhedrons 15. Numerical results using 20-HSAPP show that BER = 1×10-6 with an OSNR of 0.5dB could be achieved with a back-to-back configuration.
Here, we propose a hybrid subcarrier/amplitude/phase/dual polarization (H-SAPDP) system for optical transmission of 300 Gb/s. To improve performance, the system is based on polyhedrons. We demonstrate that the proposed system can be significantly banked to the Shannon limit over optical channels of different distances using WDM techniques.
The use of multidimensional modulations is a novel technique that holds promise for future generations of communication systems with both enhanced SE and superior BER performance. The SE and BER performances are known to be inversely proportional to one another according to the Shannon theory. In addition, the system may suffer from distortion effects if larger amounts of information are transmitted. However, the use of multidimensional techniques mitigates these challenges because, if the amount of information increases, it can be packaged by an interleaving bit distribution process to generate an N-dimensional lattice. This approach reduces the bit error rate, the inter-symbol interference, and the power transmission and consequently increases the SE as if two different modulations were being used at the same time: high-index modulation to improve the SE and low-index modulation to enhance the BER performance.
The proposed technique is implemented with different lattice dimensions in the interleaver process: a hypercubic multidimensional lattice with 16 symbols for 12 bits in an even alignment, and a polyhedron-spherical lattice with 32 symbols for 13 or 15 bits in an odd alignment. 12_13 or 15 bits are allocated to each block and packed with three sub-carriers composed of DP signals (I X , Q X , I Y , Q Y ) and aligned in parallel (i.e., they transmit at the same time). One bit is added to denote the change from even to odd alignment; thus, the packed block will have 5 bits and, consequently, the distribution packing can be set in the range of 13-15 bits.
Finally, this packaging is transformed into a 4D optical signal using Jones vectors and Pauli matrices designed according to the parameters of the polarized signal. Thus, the H-SAPDP system performs dual-lattice packing with multidimensional modulations at 50 Gsymbols/s. In this way, the binary input is divided among the 4D carriers for transmission over a distance of 50, 80, or 100km. This approach is compared with dodecahedral techniques based on the Poincaré technique and with different-dimensional packing.
Several possible constructions for the packing lattice have been proposed. However, unfortunately, this remains an unsolved problem in mathematics. The face-centered cubic lattice is obtained using a generator matrix in which the vectors represent the deep holes that arise from sphere packing (referred to as glue vectors). Another strategy is to consider the kissing number, which represents how many spheres can be arranged so that they all touch one central sphere of the same size 16. In this study, we base the lattice on the theory of the sphere-packing problem which can be observed in the orange pyramid in fruit stands. Using this lattice configuration, the advantage of the triangles found in pyramids leads to geometrically equivalent packings.
To be precise, herein, we define the thickness (also called density, sparsity or coverage) as the number of spheres that contain a single point in space.
The remainder of this paper is organized as follows. Section II presents a description of the optical system considered here and the H-SAPDP coded modulation, the dual lattice used to build the cubic and spherical lattices (Section II-A), the interleaver process (Section II-B), the multidimensional modulator (Section II-B), and Stokes and polarized signal parameters (Section II-D). The numerical results of the simulation are presented in Section III. Finally, the conclusions are summarized in Section IV.
H-SAPDP CODED MODULATION
There are many ways of building a constellation lattice in order to optimize the signal constellations using N-dimensions. Fig. 1 shows different methods of polarization over an optical fiber. Previously, 4D formats with single-polarization and switch polarization were severely limited due to the synchronization of X and Y signals (Fig. 1(b) and Fig. 1(c)) 17. Today, it is possible to modulate different signals with orthogonal X and Y polarization with total dependency between them. Thus, we leveraged the four dimensions of the optical carrier field as shown in Fig. 1(d) in order to transport 16-point rectangular constellations and 28-point circular constellations through a cube and hypercube respectively in the 3D with total independence among them.
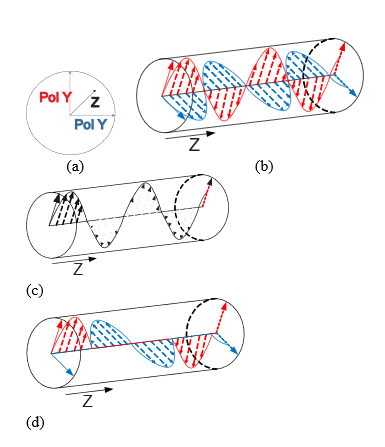
Fig. 1: Optical wave polarization techniques (a) Axis, (b) Single polarization, (c) Switch polarized, and (d) Dual polarization.
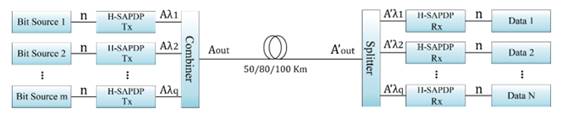
The proposed system, shown in Fig. 2 is composed of m-bit sources of n bits. Each source inserts input bit streams to the H-SAPDP transmitter to obtain a 4D lattice for each sub-carrier, A q . These carriers transmit modulated optical pulses to achieve different constellations, as shown in Fig. 5 (i.e., a cubic or spherical lattice, which are described later; Fig. 6). All the carriers are combined and transmitted by a single-mode optical fiber. Finally, at the receiver end, an optical splitter divides the optical carriers to recover the information.
Fig. 4(a) shows the general block diagram of the H-SAPDP transmitter which accepts m-bit inputs from the information sources, passes them through a set of identical LDPC encoders with a code rate of R = k/n, where k represents the number of information bits that the encoder accepts and n the length of the resulting codeword. The encoded data from these branches is forwarded to an m×n; block interleaver where it is written row-wise and read column-wise. In addition, the interleaver process performed by a dual-lattice multidimensional D N ×D N ; building matrix that is defined based on the lattice-packing process.
Dual Lattice DN
The checkerboard lattice is defined as D
N
= {(x
1, … , x
N
) 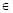 ZN: x1 + … + xN}, where the four-dimensional lattice D4 is the most useful and defined by the following generator matrix described in (16). The packing radius is normalized at ρ= 1/2:
ZN: x1 + … + xN}, where the four-dimensional lattice D4 is the most useful and defined by the following generator matrix described in (16). The packing radius is normalized at ρ= 1/2:
In our packing design, we adopted the generator matrix of four-dimensional lattice in order to integrate over 12, 13 and 15-dimensional lattices D N ∗ X D N ∗ that are explained later in the next scheme
Interleaver Process
The information that is output by the encoder is grouped into different N-dimensional lattices to obtain the multidimensional modulation matrix M and, subsequently, form the output bitstream m. However, we propose packaging strategies with 12, 13, and 15 bits in order to build N-dimensional lattices. In this way, different types of multidimensional dual-lattice packing, with different signal polarization parameters are used to obtain different signal constellations (Fig. 5 and Fig. 6). The signal polarization parameters based on the Stokes theory are described in the next section.
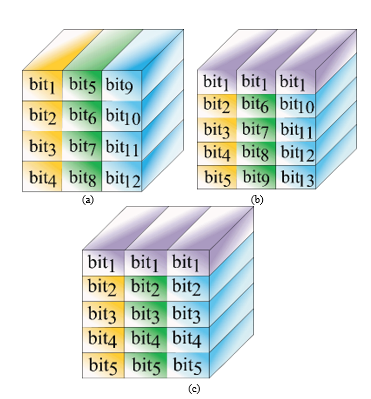
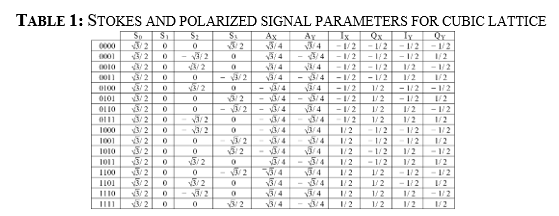
Fig. 3 shows the interleaver bit distributions for 12, 13, and 15 bits, which are evaluated in terms of performance and compared with previous results presented by Hussam in [14] to optimize the interleaver. 4D multidimensional packages of 16 symbols can be transmitted independently using four Stokes parameters as well as quadrature phase-shift keying (Q-PSK) and IQ modulation, each with both polarizations (X and Y) as shown in Table I. To package 12 bits in an even alignment with a 4D constellations (Fig. 5) shows for each sub-carrier, λq, the bits are packaged in 12 dimensions, D N ∗ X D N ∗ where the rows are written based on each vector of M, forming the block shown in Fig. 3(a).
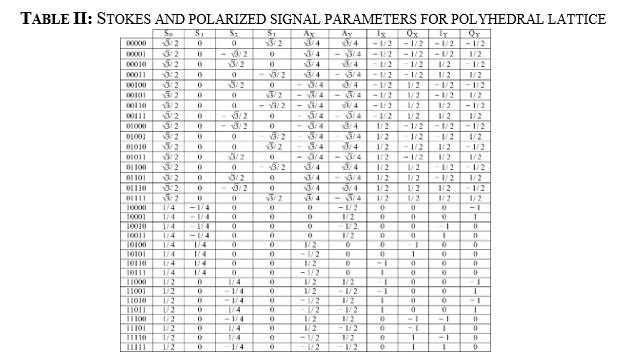
For the 13 bit odd alignment, we use 32 symbols per sub-carrier to form the polyhedral and hypercubic multidimensional constellations (Fig. 6). The first column shows the odd bits, which are defined according to the most significant bit. These are used to decide whether to use the 16 symbols shown in Table I or the remaining 16 symbols shown in Table II. To maintain consistency in the data interleaving, the first dimension of the packing must contain bit1 for every sub-carrier as shown in Fig. 3(b).
Similarly, for 15 bits in an odd alignment, 32 symbols are used for each sub-carrier. However, the interleaver bit distribution is packaging 5 bits inside each sub-carrier to obtain the block shown in Fig. 3(c).
Multidimensional Modulator
The symbol-mapping process is defined based on X-Y polarization information according to the lookup tables (LUTs) presented in Tables I and II to generate a 4D cube or polyhedron, respectively, as described in [18].
The 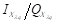 and
and 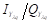 driving signals in the mapper output pass through the zero-insertion training symbols process defined as eight times the q-carrier frequencies (i.e.,
driving signals in the mapper output pass through the zero-insertion training symbols process defined as eight times the q-carrier frequencies (i.e.,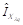 ), then, the signal is inserted to Multidimensional Modulator Block as is shown in Fig 4(a) and detailed in Fig. 4(c).
), then, the signal is inserted to Multidimensional Modulator Block as is shown in Fig 4(a) and detailed in Fig. 4(c).
The modulation process uses a fiber ring with an internal phase modulator and an erbium-doped fiber amplifier (EDFA) to compress the laser pulses in order to generate an ultrashort pulse width of 1.77ps. This optical oscillator is called the mode-locked fiber laser (MLFL) [19], using periodic rectangular pulses 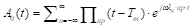 , where np is the number of infinite pulses, Tm = 1/fm where fm is frequency of the modulator at 50 GHz [20].
, where np is the number of infinite pulses, Tm = 1/fm where fm is frequency of the modulator at 50 GHz [20].
Then, A0 (t) signal is divided by an optical splitter with the corresponding wavelengths, which is represented in the same way as two mutually orthogonal components of the electric field in a plane perpendicular but it is taken with optical frequency, defined in the same way (1):
where, X/Y has the probability of being X or either Y, defining them as the different polarization phases, which are both corrupted by the same phase noise of the transmitter.
Once the ultrashort pulses are input to PBS, it is branched for the X and Y polarization to obtain the instantaneous amplitudes of the two orthogonal vectors both modulated by In-phase Quadrature Mach-Zehnder Modulator (IQ-MZM) [17], which is shown in Modulator Xλq and Modulator Yλq blocks in the Fig. 4(c). These blocks are composed by two Mach-Zehnder Modulators (MZM) each one, which were used to modulate the electrical signals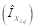 ,
, 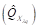 , and
, and 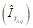 ,
, 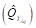 in light intensity , thus in this way we generate at the output of MZM an optical signal with in-phase and quadrature components respectively. These equations are described below:
in light intensity , thus in this way we generate at the output of MZM an optical signal with in-phase and quadrature components respectively. These equations are described below:
where A0 is the amplitude pulse normalized at 1 and:
where Vπ is the voltage equal to 2.5V in order to achieve a phase shift. Thus, the modulated pulse for X and Y polarization are represented as follows:
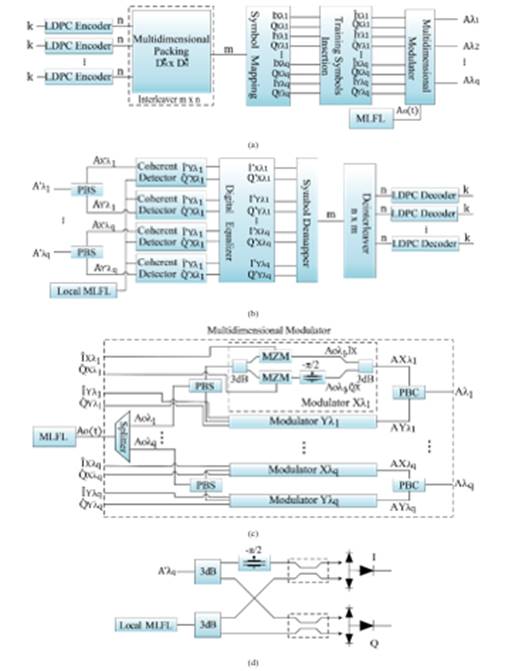
Fig. 4: H-SAPDP System (a) Transmitter Scheme, (b) Receiver Scheme, (c) Multidimensional modulator scheme, and (d) Coherent Detector scheme
Thus, the polarized outputs 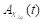 and
and 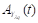 are combined by Polarization Beam Combiner (PBC) to obtain A
λq
as the modulated signal for q subcarrier.
are combined by Polarization Beam Combiner (PBC) to obtain A
λq
as the modulated signal for q subcarrier.
Stokes and Polarized Signal Parameters
Based on the coherent properties of a light beam, the spin angular momentum defines the polarization state and the orbital angular momentum is associated with the azimuthal phase structure but is independent of the spin parameter. A geometric representation of the polarization state called the Jones vector was proposed in 1892; the amplitude and phase of the Jones Vector represent the 2D complex vectors of the electric field.
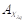 and
and 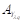 are used to denote the amplitudes of the waves in the two components of the electric field vector and their respective phases. The product between a Jones vector and a complex number gives a different Jones vector represented in the same state of polarization.
are used to denote the amplitudes of the waves in the two components of the electric field vector and their respective phases. The product between a Jones vector and a complex number gives a different Jones vector represented in the same state of polarization.
To represent the monochromatic Stokes parameters 22 as a linear expansion, we use the Jones vectors of the instantaneous electric field as elements of the coherency matrix of the n-th wave and combine them by Pauli matrices 21, where any wave may be regarded as the sum of independent waves (completely unpolarized and completely polarized waves):
Next, the coherency matrix is written as the conjugate of each element in the matrix, which produces a Hermitian matrix, as follows:
The Stokes parameters are physically measurable and are properties represented as 23:
The coherency matrix is not easy to visualize, so that we describe the partially polarized radiation in terms of the total beam intensity (S 0). S 1 and S 2 denote the azimuthal phase information for the right and left circular polarization, respectively and S 3 is defined as 24. Thus, the Stokes parameters can be written as functions of the intensity and polarization, where the intensity is referred to at Jones Matrices and the polarization is referred to at Pauli matrices. Thus, the Stokes parameters are defined as follows:
Then, the outputs of the H-SAPDP transmitters are forwarded to a combiner before being transmitted via the optical fiber. On the receiver side, as shown in Fig. 4(b), the signal is split into λ q branches, forwarded to the H-SAPDP receivers, and sampled at the symbol rate.
The process of information recovery begins by using a PBS to separate the X - Y polarized information from A'λ q to retrieve the IQ signal through the coherent detector composed by an MLFL as local oscillator (LO) and an internal phase modulator in order to compare the input and LO signals to obtain the IQ electrical signals, as shown in Fig. 4(d).
All the IQ polarized sub-carrier signals are forwarded by a digital equalizer in order to compensate the obtained signal by removing the training symbols by applying the intra-symbol frequency-domain averaging channel estimation technique developed previously 25.
Next, demapping was applied to these signals to yield 16 or 32 multidimensional symbols placed in cubic or spherical lattices, respectively, as shown in Fig, 5 and Fig. 6, respectively, to form a hypercube or polyhedron, respectively. Based on the theory of molecular links, the use of these geometric figures can reduce the symbol energy due to grouping and allow more data to be transmitted. Then, the output signals are forwarded to deinterleaver and, finally, to the bit log-likelihood ratio calculator which provides N LDPC decoders with the appropriate code rate, [k/n]. This process helps to improve the system performance (i.e., reduce the BER) without increasing the system’s complexity.
Multidimensional Simulation Setup And Numerical Results
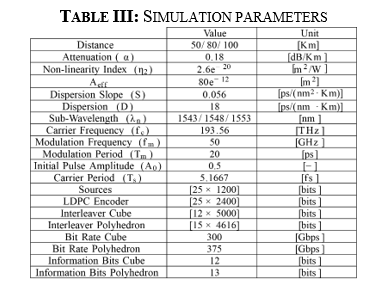
The functionality of the H-SAPDP LDPC-coded-modulation system was tested by simulation in MATLAB based on the parameters shown in Table III, the optical parameters proceed to SMF-28 Ultra optical fiber due to low attenuation and polarization mode dispersion index
According to Fig. 4(a), the simulation setup feed by m= 25 parallel data sources, each source is coded by LDPC Encoder which the code rate is R= 1/2. The Interleaver block reshapes the information into different N-dimensional lattices in the way described in Section II.B, next the coded data are divided in order to translate the binary information into driving voltage signals through Table I or Table II for each subcarrier, depending on dimensional alignment, to feed the multidimensional modulator described in Section II.C.
For the DP pulse propagation, the split-step Fourier method extension presented in 26 was used to present the Schrödinger propagation at the single-mode in the X-Y plane.
In the first scenario, the BER performance was analyzed for a 4D signal transmitted through each 4D sub-carrier λ1,…,λ q , with 12 bits. The symbol data constellations were built according to polarized signal parameters as shown in Table I in order to represent the 16-points in 3D. Fig. 7(a) shows the results after transmission over distances of 50, 80, and 100 km. The best result was obtained over 50km, exhibiting a very close response with an OSNR of 6dB and a BER=10-6. The transmission rate, defined as the product of the number of sub-carriers, the modulation frequency, the bits transmitted and codification rate (3×50×4×0.5), was 300 Gbps.
The performance in terms of BER was excellent compared to that achieved using traditional modulation techniques with 2D dimensions over a transmission distance of 100km. Moreover, the proposed hybrid technique made it possible to transmit more information (up to 256-QAM) while, at the same time, reducing the OSNR.
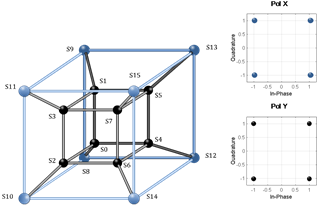
Fig. 8(a) shows the 4D constellation diagram mapped in 3D space for one sub-carrier. This was the expected result of the hypercube construction based on the molecular technique with identical inscribed polygons. The OSNR in the back-to-back configuration was set to 10dB to visualize the multidimensional system noise. The hypercube was generated by setting the height and length in the first two dimensions based on the I Y /Q Y data, the width in third-dimension was set based on the Q X data, and an internal or external cube was selected (i.e., the fourth dimension based on the I X data. In this way, the 4D symbol generates the lattice despite the noise to facilitate suitable robust transmission.
Similarly, Fig. 7(b) shows the BER performance when an odd alignment was used to generate a 4D polyhedron constellation for each sub-carrier.
With the polyhedron technique, a gain of 2 dB in terms of the OSNR was achieved for 12-bit transmission over 50km while transmission over 80 and 100km resulted in a 3dB OSNR gain. Furthermore, the BER was approximately 10-6 for 12-bit transmission. In this context, it is more convenient to work with an additional bit but the same performance cannot be achieved with 15 bits due to the packing process.
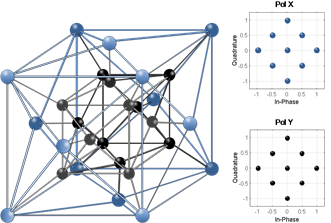
As the multidimensional system noise sensibility for the 4D-polyhedron constellation is presented in Fig. 8(b) shows the result when a back-to-back configuration is used again, the OSNR was set at 10dB to visualize the hypercube and polyhedron techniques under the same conditions.
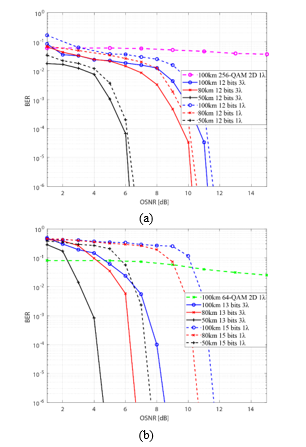
Fig. 7: BER performance analysis (a) with a 4D cubic lattice (even alignment) and (b) with a polyhedral lattice (odd alignment).
In the non-linear effect, the spectral envelope gives rise to a wider peak power due to chromatic dispersion and non-linear phase variation on X-Y plane; this effect generates new optical frequency components as the pulses propagate.
It is important to note that this non-linearity effect is due to transmission distance and the wavelength compression due to data packing for single-channel transmission. In this system, increasing the wavelength could cause a distortion in the system and, consequently, degraded the SE. However, with three sub-carriers the SE and BER are very stable over long distances, as shown in Fig. 10 and Fig. 11. Note that the effect of wave mixing occurs when N-subcarriers are used. However, it is not necessary to analyze the non-linearity or implement compensation to avoid channel interference, for the reasons described previously.
Spectral density (PSD) was obtained using (10), where T s is the period for a pulse and R (k) represents the pulse autocorrelation defined in (11) for a bipolar RZ signal.
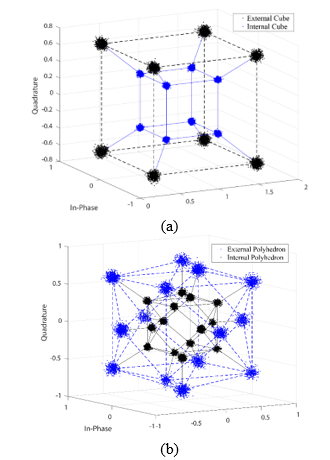
Fig. 8: 4D Geometric (a) Back-to-back representation of the 4D cubic lattice (even alignment) with an OSNR of 10dB and (b) Back-to-back representation of the 4D polyhedral lattice (odd alignment) alignment) with an OSNR of 10dB.
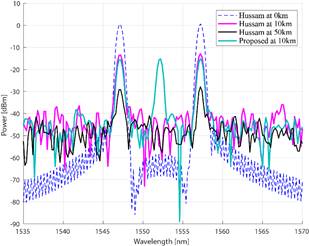
PSD comparison between system proposed H-SAPDP with Hussam at OSNR = 5dB.
Given the complex envelopment signal, A OUT , the PSD function in Equation (10) can be rewritten as follows:
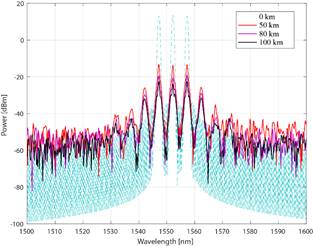
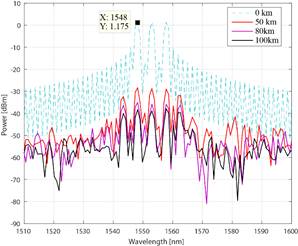
The PSD in Fig. 9 shows that two new frequency components occurred at 1542 and 1562nm due to chromatic dispersion over the propagation distance. This secondary frequency has 13.66% less power than the central pulse peak power at a transmission distance of 50km.
The Hussam system supports up to 10km of distance using two sub-carriers. Fig. 10 shows the comparison between Hussam and the proposed method in terms of PSD. H-SAPDP remained superior compared to the Hussam system using even one additional sub-carrier. The SE in Hussam method at 50km is already degraded.
We further compare the BER performance using the proposed system with the Poincaré technique developed by Hussam and our HSAPDP proposal over 10 km and 50 km respectively. Fig. 11 shows the simulation results among these two techniques, where the 10 km scenario presents an interesting result of OSNR = 4dB and a BER=1×10-8 for the Poincaré technique, however, the proposed technique has a gain of 0.5dB and 1dB for 12-bit and 13-bit multidimensional format, respectively.
On the other hand, the 50km scenario shows a high error level of BER = 1×10-1 for the Poincaré technique, meanwhile, the proposed technique achieves a BER = 1×10-8 at 6.5dB and 5dB of OSNR for 12-bit and 13-bit multidimensional formats respectively. As is shown, there exists a gain of 1.5dB and 0.5dB in terms of OSNR between 13-bit and 12-bit multidimensional formats. In this context, the Poincaré technique involves the use of a dodecahedral geometry for symbol mapping in 3D space, but this technique cannot be supported beyond 10km of distance while, in contrast, we demonstrated that our systems can be used for long transmissions at different wavelengths. In this context, the Power Spectrum degradation is negligible between 80km and 100km of distance as is shown in Fig. 9.
Also, in order to achieve a beyond 1Tb/s transmission, our proposed is evaluated over optical time-division multiplexing (OTDM), based on the Nyquist filter combined by MLFL to generate a Nyquist pulse train 27. In the reception, a homodyne coherent detection achieves (3×50×4×0.5) × 4 timeslots = 1.2Tb/s transmission for 12-bit system and (3×50×5×0.5) × 4 timeslots = 1.5Tb/s for the 13 bits system based on the definition of the transmission rate used previously, improvement the rate of 320 Gb/s over 4-time slots for OTDM-DQPSK and a homodyne coherent detection scheme presented in 28
Fig. 11: Comparison of BER Performance between system proposed HSAPDP and Hussam over 10km and 50km.
The simulation results, expressed in Fig. 12, show the power reduction over the OTDM transmitted signal. Here, we can compare the spectral efficiency between OTFDM-DQPSK systems and our proposal of Fig. 9. In order to demonstrate that our systems can increase the velocity, but its spectral efficiency is worsened. In conclusion, our system is widely affected when it is used the OTDM signal, having a penalty of 12 dB with respect to the non-OTDM signal. This reduction of peak to average in the OTDM signal is due to Nyquist pulse compression, which is used to OFDM signals [29]. Consequently, the SE is degraded even more if the distance is increased. Concluding in this way, that there exists a trade-off between the transmission rate and the Spectral Efficiency due to the time-multiplexing degrade, is being this very important penalty to consider when the system can be implemented at high-speed data transmission.
Conclusions
In this study, we demonstrated that the novel H-SAPDP LDPC-coded-modulation system can improve the BER performance for long-distance transmission. In addition, we demonstrated a novel technique based on the Poincaré sphere and Stokes parameters to achieve more data packaging in the 3D space. The results are promising since the multidimensional modulation can achieves high data transmissions in the same way that high-index traditional modulation format but using a grouping of two polarizations for each subcarrier either in 12 bits and 13 bits. In this way, we transmit with less energy per symbol improving the spectral efficiency and BER performance at the same time.
Moreover, we implemented the Pol-Mux technique over the WDM system using three sub-carriers to achieve 12 bits-even alignment, which is not possible with another type of 4-D independent carrier modulation. We further expanded the technique to be N-dimensional for handling 13 and 15 bits-odd alignment. Finally, cubic and polyhedral constellations were used in the three-dimensional plane to demonstrate that our proposed exceeds the Hussam method. Results reveal the efficiency of BER performance at 3 dB and 0.3 dB for odd and even configuration respectively in traditional systems with the only-one subcarrier. Also, our proposal can support greater distance with spectral efficiency penalty negligible respect to Hussam method.
From a system general performance perspective, a 13-bits odd configuration offers more robust transmission compare to a simple 4-D transmission over single-mode fiber. On the other hand, the analysis performance considering the shape lattice between rectangular (12-bits) and cross-constellation (13-bits), we conclude that 13-bits is the ideal method in order to implement over real systems. The numerical results reveal an important gain in terms of Optical-SNR when the systems supported at 100km of distance. We obtain around 8.5dB of OSNR with a BER = 1×10-6 using the max distance. Another relevant aspect, our proposal has a gain compared with the traditional multidimensional modulation using one-carrier. The gain corresponds to 3.7dB for all distances (50/80/100km) when 3λ were used.
In future studies, the SE can be improved further by analyzing the non-linear channel formed due to the increased number of sub-carriers. Moreover, to apply new techniques of compensating for the four-wave-mixing effects, the number of lambdas should be increased in future iterations of the system. Additional to increase the number of subcarriers, we could to study the allocation of wavelengths in order to improve the spectrum efficiency and power consumption in the system. This study will bring us to deepen the elastic networks for the future generation.