1. Introduction
New corona -viruses appear to emerge periodically in humans, mainly due to the high prevalence and wide distribution of corona-viruses, the large genetic diversity and frequent recombination of their genomes, and the increase of human-animal interface activities (Zhu, 2019). "In late December 2019, a number of local health authorities reported clusters of patients with pneumonia of unknown cause, which were epidemiological linked to a seafood market in Wuhan, Hubei Province, China". (Zhu, 2019). In the province of Santo Domingo de los Tsáchilas the first positive case of SARS-COV-2 was registered in a person who resides in the city of Santo Domingo, but works in the city of Manta. “In Santo Domingo the number of positive cases increased exponentially” according (SNGR, 2020). The provincial, cantonal and parish Special Operations Committees (SOC) took measures such as completely suspending the mobilization of urban and inter-provincial buses, taxis and curfews for intervals of time to minimize the dynamics of people.
Santo Domingo de los Tsáchilas is a province with 368 013 inhabitants according to (INEC, 2010), at present (10 years later) it is estimated to have a population of 500 000 inhabitants according to a survey carried out by the same institution. It is one of the most transient provinces of the country, because it is one of the main passages from the coast to the mountains, it also hosts a diverse population as there are people who have come from all over Ecuador.
In view of the imminent arrival of the 2019-nCoV disease pandemic, the authorities of the province and the country have taken several strategies to stop the spread of the virus in the population. The preventive measures taken by (GadStoDgo, 2020) the Minister of Government and Minister of Education are:
Ø Restriction for passengers who during the 14 days have been in Hubei and Wuhan in China, Italy, the Kingdom of Spain, France, the Islamic Republic and Iran.
Ø Mass events are suspended and public events of more than 1000 people.
Ø The ban is also for night-time entertainment establishments because they are closed places.
Ø Lifetime Brigades are suspended, except for medical brigades throughout the country.
Ø 2019-nCoV testing will be authorized to qualified laboratories in other cities.
Ø Alert platform for possible cases of Corona-virus.
Ø There are 22 hospitals throughout the country to attend to cases, of which 1 is in Santo Domingo.
Ø Classes will be suspended throughout the country.
Ø Curfew is in place at intervals throughout the country.
The purpose is to model and try to extract the significantly important aspects of this real situation, to translate them into expressions and differential equations of models used for previous pandemics. First, the most common mathematical model (SIR) for this type of pandemic will be implemented, and later others with particular adaptations to the 2019-nCoV corona-virus epidemic, such as the one called (SEIR), to which changing parameters are incorporated in order to simulate the measures taken by the national government that influence the entire country, as in Santo Domingo de los Tsáchilas. Consider that we are not trying to make a real prediction with concrete numbers, in which we would need more technical data to try to approach reality with less margin of error, but rather to show the influence of the measures taken by the authorities on the development of the epidemic.
1.2. Theoretical background.
A new human corona-virus, now termed 2019-nCoV, emerged during December 2019 in the Chinese city of Wuhan. As of 1900 GMT 24th January 2020, over 900 cases have been reported in China (with 26 deaths), and cases have been detected in at least 9 regions or countries outside mainland China. Initial phylogeny analysis suggests that the new virus is similar to the SARS corona-virus when compared with other corona-viruses known to infect humans (Imai, 2020).
This led several groups of Chinese scientists to identify a new type of corona-virus. The high spread of the infection accelerated studies in Wuhan City and Hubei Province, China, considered the epicenter of the outbreak.
On January 30, 2020, the World Health Organization named the new virus SARS-CoV-2, called the type of pneumonia that produces the virus 2019-nCoV, and declared a global medical emergency.
Corona-viruses are a type of single-stranded RNA virus, which affect animals and humans, causing respiratory, liver, gastrointestinal and even neurological diseases. This type of CoVs is divided into four classes: alpha-corona virus, beta-corona virus, gamma-corona virus and delta-corona virus. Currently, 6 types of human corona viruses have been identified, including SARS-CoV and MERSCoV, responsible for respiratory disease pandemics reported in 2003 and 2012, respectively (Li R, 2020).
Several factors seem to influence whether corona viruses are related to humans, "including the prevalence, wide geographical distribution of these viruses and increased interactions between humans and animals, especially wildlife" according to (Castro, 2020).
SARS-CoV-2 has a zoonotic origin (not yet identified), it is a positive single-stranded RNA beta-coronated virus, as are SARS-CoV and MERS-CoV.
The number of people an infected person can infect is known as Re (effective reproduction number). According to (Li R, 2020) "the effective reproduction number Re is estimated to be 2.38 (95% CI: 2.04 - 2.77), which shows a high capacity of the virus to sustain transmission over time". Rulers should look for mechanisms to reduce it to numbers below 1, considering that the pandemic is under control.
1.3. SARS-CoV-2 infection
A person can get COVID-19 from contact with another person who is infected with the virus. The disease can spread from person to person through droplets from the nose or mouth that are released when an infected person coughs, sneezes, or breathes out. These droplets land on surfaces and objects around the person, causing other people to come into contact with the virus by touching these surfaces or objects, and can contract VID-19 if they touch their face, allowing the virus to enter the body through the nose, mouth, and eyes. There is also a risk of infection if droplets released by sick people are inhaled. This has led to the three main recommendations: keep at least one meter between people, wash your hands frequently and avoid touching your face with unwashed and/or disinfected hands (OMS, 2020).
1.4. Incubation time
The manifestation of the first symptoms is around 5 days, average incubation time according to several contributions. "A study on a sample of 180 confirmed patients establishes that the median incubation period was estimated at 5.1 days (95% CI, 4.5 to 5.8 days). Furthermore, it was concluded that 97.5 % of the patients developed symptoms in 11.5 days (IQ, 8.2 to 15.6 days) of infection" according to (Lauer, 2020). In this publication they conclude that after 14 days of active monitoring or quarantine 101 out of 10,000 cases (99th percentile, 482) will develop symptoms. (Wu, 2020) Similar estimates are given in.
In recent publications, the mean incubation period of CoVID- 19 was a little bit different, “with 138 cases, reported that the median durations from first symptoms to dyspnea, hospital admission, and acute severe respiratory syndrome (ARDS) were 5 days (range, 1–10), 7 days (range, 4–8), and 8 days (range, 6–12)” respectively (Wang, 2020).
Instead “with 425 confirmed cases, instructed that the mean incubation period was 5.2 days (95% confidence interval [CI], 4.1–7.0), with the 95th percentile of the distribution at 12.5 days. In its early stages, the epidemic doubled in size every 7.4 days. With a mean serial interval of 7.5 days (95% CI, 5.3–19), the basic reproductive number was estimated to be 2.2 (95% CI, 1.4–3.9)” (Lin, 2020). While (Guan, 2019), “with 1099 patients, reported that the estimated mean incubation period of SARS-CoV-2 infection was 3.0 days (range, 0–24.0), which was shorter than in the two research reports above (3.0 days vs 5 days and 5.2 days).
1.5. Symptoms
Symptom of CoVID-19 are non-specific and the disease presentation can range from no symptoms (asymptomatic) to severe pneumonia and death. A study of 41 patients (Huang, 2020) “who were initially diagnosed with the outbreak (the diagnosis date was up to 2 January) found that the most common symptoms were fever (98%), cough (76%), myalgia or fatigue (44%); and atypical symptoms included sputum (28%), headache (8%), hemoptysis (5%) and diarrhea (3%)”.
Also (Huang, 2020) “found that the most common symptoms were fever (87.9%), cough (67.7%), diarrhea (3.7%) and vomiting (5.0%). 25.2% of the patients had at least one underlying disease (such as hypertension, chronic obstructive pulmonary disease).”
2. Methodology
As a research methodology, the collection of information was through surveys with a 95% confidence sample in the province of Santo Domingo de los Tsáchilas, which according to (INEC, 2010) "estimates a population of 500 000 inhabitants". The information was obtained through a survey; this was sent by telematic means due to the high risk of contagion of the virus. This causes a bias in the real data because not all the interviewees work full time, some are teachers who work from home, but all can qualify the measures adopted by the authorities.
To determine the parameters (rigidity of the containment measures) α, (social impact of the pandemic) k, several questions were asked to quantify on a scale of 1 - 5, descriptive statistics were applied to have the real values of the parameters in the which is evidence of extreme public concern in relation to the 2019-nCoV, and disagreement with the containment measures taken by the authorities. Section 3.1 provides an example of the SEIR model in which no actual data is used.
In section 3.2 for modeling and simulation in current scenarios, α = 3.22 (95 % CI: 3 - 4) and for k = 4.10 (95 % CI: 4 - 5) was set, for MatLab modeling, a rule of three was made Simple in relation to the unit for α (various scenarios of containment measures) and for k a scale of 100 was considered as proposed (Lin, 2020). Finally, β (t) is considered with the variation of measures.
2.1. Methodological example about Epidemiological Model SEIR
The main hypotheses formulated to build these models are in other pandemics such as SARS (Li, Wang & Jin, 2006):
Ø The disease that is modeled confers immunity to the people who recover.
Ø The total population N is constant, S(t) + E(t) + I(t) + R(t) = N∀t. This implies that births and deaths in the period are negligible and that the disease does not It is mortal;
Ø The population is uniformly distributed in the considered region;
Ø The rate of increase of E is proportional to the number of contacts between S and I (since the flow is unidirectional, all new exposed comes from the population susceptible); and
Ø The rates of decrease of S, E, and I are proportional to S, E, and I, respectively (since the more extensive the population, the more individuals are exposed, infected, or recovered in each case). Likewise, the increase in R is equal to the decrease in me.
This model, being an extension of the SIR model, demonstrates the importance of epidemiological fences, since a new variable (exposure to infection) is included and therefore a new E(t) equation. Then we denote, if an individual does not present symptoms, but can infect others we count it in I(t), not in E(t).
The relationship of the new variable E(t) with I(t) leads to a new parameter θ, so that 1/θ is the average incubation time. So, the new class of individuals who carry the E(t) disease but who, being in their incubation period, do not show symptoms and cannot yet infect others, for example, people in the inner circle of people already infected or people who have had interaction with infected people in public transport systems, etc. It's true that: S(t) + E(t) + I(t) + R(t) = N
In figure 1 we have a sequence of the functions, in relation to the parameters for the SEIR model.
In figure 2 we have the system of differential equations for the SEIR model:
An example using the SEIR method is presented in figure 3, with population N = 100 000 people, parameters β = 1 , ɣ = ¼ , θ = 1/5 and initial values for the functions E(0)=5 ; I(0)=1 ; R(0)=0.
An example using the SEIR method is presented in figure 4, with population N = 500 000 people, parameters β = 0.5, ɣ = 1/5 , θ = 1/7 and initial values for functions E(0)=10 ; I(0)=1 ; R(0)=0.
An example using the SEIR method is presented in figure 5, N = 500 000, parameters β = 0.75 , ɣ = 1/5 , θ = 1/7 and E(0)=10 ; I(0)=1 ; R(0)=0.
An example using the SEIR method is presented in figure 6, N = 500 000, parameters β = 1 , ɣ = 1/5 , θ = 1/7 and E(0)=10 ; I(0)=1 ; R(0)=0.
2.2. Epidemiological model for COVID-19 with government containment measures
In Ecuador, several measures have been taken since the first positive case of the epidemic, considering that the public health system may collapse as in all affected countries. The population has not taken sufficient precautions to try to stop the spread of the virus, even though the government provides for social isolation measures such as quarantine and curfews for intervals of time there is mobility and social dynamics. Ecuador, according to (INEC, 2020) "has an unemployment rate of 3.8 %", which is why people continue to take to the streets and this becomes a determining factor in the growth of the number of infected people who are symptomatic or asymptomatic.
In order to describe the spread of the disease and the behavior of the virus, several studies have taken into account other types of individuals, such as those who always remain asymptomatic (which may affect others) or those who never become infected (this seems to be the case with children), among other parameters related to quarantine, government measures and the periods of diagnosis.
The virus mutates according to population dynamics, which causes different measures to be taken in different countries. At the end of 2019 in Wuhan, studies focused on local variables, such as infection directly from contact with animals, as well as the extraordinary population movements resulting from the Chinese festivities of the time.
As we have been saying, what is unnecessary when studying the dynamics of an epidemic is to propose a model (in this case SEIR) and to know the value of the parameters involved: β, ɣ and θ.
According to (Lin, 2020), "1/ɣ = 5 days and 1/θ = 7 days (these numbers are approximate averages, and may vary quite a bit from person to person)". A real challenge is to estimate β; because you don't have the real local value of how many asymptomatic infected people may be infecting others.
Before they adopted drastic isolation measures in China and after several studies on the dynamics of the disease, (Wu, 2020) suggest that "the value of β could be between 0.59 and 1.68 (in units’ days-1), which would give a R0 between 2.95 and 8.4, in both cases quite high and take R0 = 2.68".
To exemplify Figure 3 and 6, the infection rate β=1 has been considered constant. However, this parameter can be artificially modified by applying protection and social isolation measures, which would be adjusted by whether or not the population complies with the provisions.
Several studies have carried out the variation in time of the parameter β, (Wu, 2020) posed a decreasing function with respect to the time of the form
E.c.1.
with βo as the infection rate without government measures, and the constants Co and Cb involve social contact (resulting from isolation from the population).
Also (Lin, 2020) proposes
E.c.2.
considering βo as the infection rate without measures, α(t) is the result of government actions represented as a constant function in chunks with a value interval between [0, 1], D(t) is the public sense of risk as a consequence of known critical cases and deaths, and k measures the intensity of the reaction of individuals.
In Santo Domingo de los Tsáchilas province, with an estimated population of 500 000, the authorities have put in place measures to try to slow the dynamics of the virus and, as expected, the population has responded in a variety of ways. This study will estimate values for the parameters β, k, ɣ, θ and α considering the response of the province's citizens, the measures taken by the authorities and the political-social difference between China and the West, which can hardly be used its same parameters, but its same modelling ideas.
As an estimate for D(t), 5% is considered, since this value represents the percentage of serious cases in the country of the total number of confirmed cases. In the value of the parameter k, some estimates are made with the information cited in (Lin, 2020) which suggests that "one can take k = 1117.3" remembering that it measures the intensity of the reaction of individuals to everything that happens with the pandemic, then considering the political-social difference and the severity of its measures we will adopt a value of k = 100. The idea of the factor in which k is an exponent, is that when k is high, the concern is much and, the factor tends to 0, people isolate themselves even voluntarily and β (t) is very small; but if the result of the factor is close to 1 it has little influence if the social concern is low.
Such that it is impossible to predict the future, we reiterate that we make estimates to analyze how the measures affect the evolution of the epidemic in the Tsáchila province; in particular, the changes in the value of α to show three scenarios, of how the epidemic would evolve from the rigor of the measures.
According to previous pandemics, the containment measures are really effective, they do not allow a very high peak curve and they move it away in time, but there is also the discipline of the population, obeying these measures would cause a positive effect in the battle against this silent but lethal enemy. So we will adopt a value βo = 1.0 and k = 100 we will proceed to vary α with three values α = 0.35 (small measures), α = 0.5 (medium measures) and α = 0.65 (severe measures).
An example using the SEIR method is presented in figure 7, with population N = 500 000 people, parameters β = 1 , ɣ = 1/5 , θ = 1/7, k = 100 and E(0)=10 ; I(0)=1 ; R(0)=0.
An example using the SEIR method is presented in figure 8, with population N = 500 000 people, parameters β = 1 , ɣ = 1/5 , θ = 1/7, k = 100 and E(0)=10 ; I(0)=1 ; R(0)=0.
An example using the SEIR method is presented in figure 9, with population N = 500 000 people, parameters β = 1 , ɣ = 1/5 , θ = 1/7, k = 100 and E(0)=10 ; I(0)=1 ; R(0)=0
An example using the SEIR method is presented in figure 10, with population N = 500 000 people, parameters β = 1 , ɣ = 1/5 , θ = 1/7, k = 100 and E(0)=10 ; I(0)=1 ; R(0)=0.
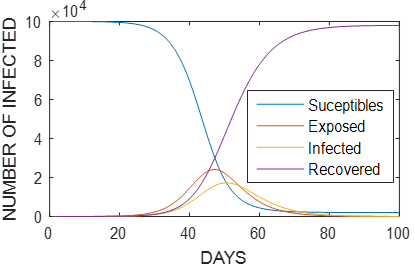
Figure 3 As in the SIR model, the infection rate is high with respect to exposure and recovery rates, generating accelerated growth of the exposed population and, subsequently, of the infected population.
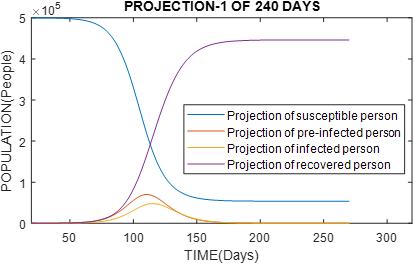
Figure 4 Graph of population with 500 000 inhabitants, reproduction rate of Ro virus = 2.5. We would have similar results to China, with high recovery rate and, the estimation of the peak of the curve in infected in 120 days.
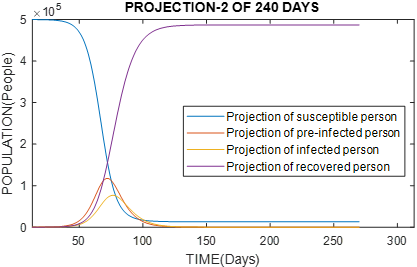
Figure 5 Graph of population with 500 000 inhabitants, reproduction rate of Ro virus = 3.75. We would have an exponential growth of infected people reaching a peak in 70 days, and a low rate of recovery.
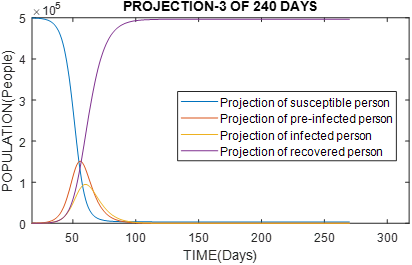
Figure 6 Graph of population with 500 000 inhabitants, reproduction rate of Ro virus = 5. it would have an exponential growth of infected people reaching a peak in 55 days, and it would be extremely difficult to control the epidemic.
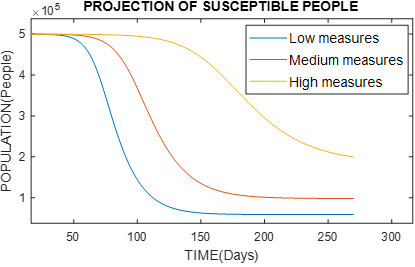
Figure 7 Graph of the behavior of susceptible people, varying the type of government measures with α = 0.35 (small measures), α = 0.5 (medium measures) and α = 0.65 (severe measures)
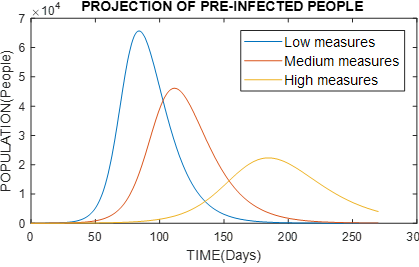
Figure 8 Graph of the behavior of per-infected persons, varying the type of government measures with α = 0.35 (small measures), α = 0.5 (medium measures) and α = 0.65 (severe measures).
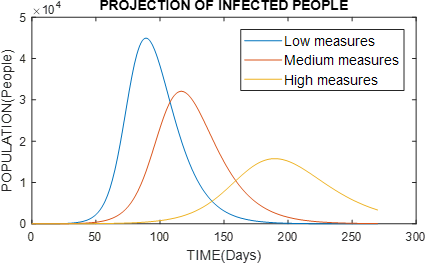
Figure 9 Graph of the behavior of infected persons, varying the type of government measures with α = 0.35 (small measures), α = 0.5 (medium measures) and α = 0.65 (severe measures).
3. Findings
Various scenarios were modeled considering the measures adopted by the authorities α = 0.35 (low measures), α = 0.5 (medium measures) and α = 0.65 (severe measures), the latter is the current scenario α = 3.23 (95 % CI: 3 - 4) that by making a simple rule of three in relation to the unit, α = 0.646 is obtained, in which possibly after 90 days we will have 497 044 susceptible, 808 exposed (pre-infected), 456 infected and, 1692 recovered. After 180 days you will have 355 958 susceptible, 22 119 exposed (pre-infected), 15 169 infected and, 106 753 recovered. After 270 days, you will have 199 828 susceptible, 4004 exposed (pre-infected), 3348 infected and, 292 820 recovered.
But for Table 1, the SEIR model was used to estimate the number of people infected in the province of Santo Domingo de los Tsáchilas considering that government measures will decrease over time since the country's economy has been affected by the falling oil prices and volatility in financial markets, which limits access to credits to cover tax debts and limits economic recovery and people will be forced to leave their homes despite the measures taken in time, with N = 500 000 inhabitants, parameters β = 1, ɣ = 1/5, θ = 1/7, α = 0.45, k = 100 and initial values E (0) = 10; I (0) = 1; R (0) = 0. All values were obtained using adjustment techniques with the official information from the investigations cited above and from the National Risk Management System.
It is expected that the measures are maintained or are more rigorous due to what is coming for the country, we all need to work, but that public policies are created that do not allow the public health systems to collapse.
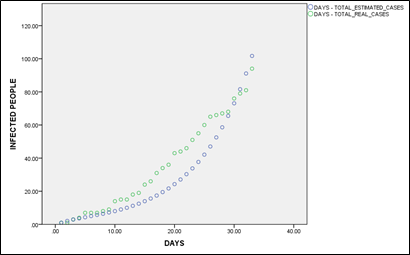
Real cases and expected cases of infected people with β = 1, ɣ = 1/5, θ = 1/7, α = 0.45, k = 100.
Table 1 Real cases and expected cases of infected people with β = 1, ɣ = 1/5, θ = 1/7, α = 0.45, k = 100.
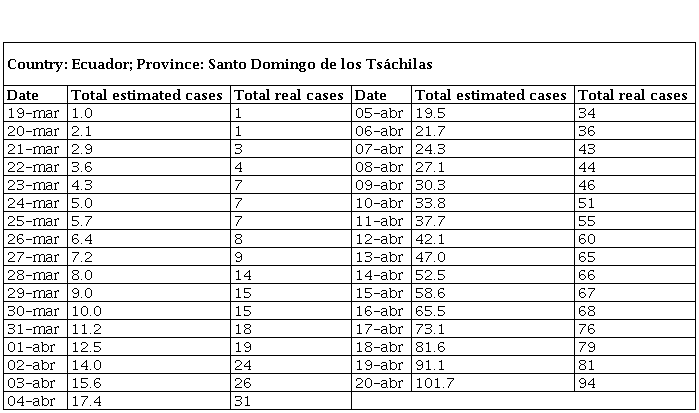
This table shows the estimated number of infected persons and the number of actual cases in the province of Santo Domingo de los Tsáchilas from the first case confirmed.
4. Discussion and analysis
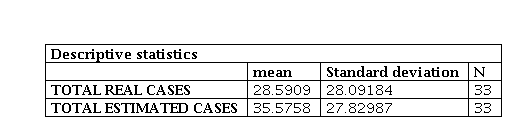
In table 2 has the mean values and the standard deviation of each variable, real and estimated cases of infected persons, being able to notice that in the real cases of infected persons the standard deviation is slightly higher (0.26197) with respect to the estimated cases, demonstrating a not considerable difference, guaranteeing even more the study because this value tends to (0).
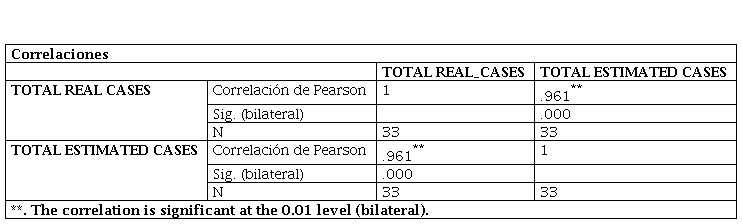
In table 3 and figure 11 considers a correlation analysis between the variables, estimated infected persons and actual infected persons using SPSS, which shows a 96% correlation, considered by (Martínez Ortega, 2009) as "a strong to perfect correlation", which means that as the number of cases of actual infected persons increases, the number of estimated infected persons also increases.
5. Conclusions
It has been proven that if severe (effective) government measures are taken in Santo Domingo de los Tsáchilas, the behavior of the virus can be significantly contained, in turn allowing the "peak" in the infected curve to be smoothed out, thus moving it away in time. It is foreseen with these parameters obtained through adjustment techniques with the official information from investigations cited above and from the National Risk Management System (α = 0.65) (government measures with severe 65 %), (β = 1) (rate of transmissibility), (ɣ = 1/5) (rate of recovery) , (θ = 1/7) (average of virus incubation), (k = 100) (intensity of reaction of individuals to the infection and number of deaths), to reach 15 169 infected people in 180 days from first confirmed case, being in the peak of the curve of infected people. Also, it must be considered that the effect of the measures is not immediate, it takes days to manifest itself according to the behavior of the population.
If we compare the severity values of the measures between (α = 0.45) and (α = 0. 65), we will have less infected in the long term with a lower alpha value, this indicates that the containment measures taken by the authorities will allow public health systems not to collapse. While if we increase the rigor of the measures, we would have more infected in the long term but we would be able to stabilize the curve with fewer infected people, allowing health systems not to collapse.
The parameter α is obtained with some concrete dispositions taken by the local authorities, in the figure 14 it is evidenced as it would be the general behavior of the number of infected people according to the severity or effectiveness of the measures, it is impossible to know beforehand, we could only estimate after what has happened; but, in any way, the effect is going to be positive, and, if in the daily evaluation of the epidemiological data it is considered not sufficient for what it is tried to achieve, stricter measures can be arranged.
Table 1 shows the comparison of the real data of infected persons according to the National Risk Management System and the data estimated from our professional perspective with parametric data, having little dispersion and a 96% correlation. It shows what is happening at present and what could happen in the medium and long term.
When preparing the battle against this type of pandemic, the main objective is to reduce the effective reproduction factor of Ro disease (flatten the curve). This influences the nature of the disease and how virulent the virus is. However, modelling and simulation reveal that there are additional factors that can be adjusted decisively for this decrease: social isolation, early detection and early mass diagnosis to rule out infected and better still pre-infected (epidemiological fence or asymptomatic people).
Having a specific scenario of social isolation (quarantine), it is expected to attack the spread of the virus in the population, reducing the early growth of the curves (not steep slope) of infected, therefore also of pre infected. This in turn is achieved with a massive identification of people confirmed with the virus, studying all people who have respiratory symptoms and not expecting people to develop serious symptoms, also all people within the epidemiological fence, they can be people asymptomatic infected. With this we avoid the blind contagion caused by asymptomatic people and, furthermore, considering that the majority of asymptomatic people have low viral load, this may be influenced by the reduction in the number of people in the intensive care units of the province and the country.
This research shows that accelerated decisions without scientific support in the face of this new coronavirus cause a rapid collapse in the public health system, and this got out of control by the unemployment rate is high. None of the measures taken by the authorities worked, and the police did not see them well; therefore, the number of infected increased exponentially. The media and the Ministry of Public Health do not show it because we are close to the presidential elections.