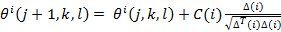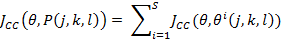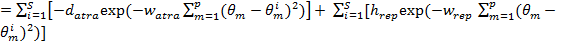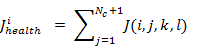1. Introducción
Several decades ago, research on optimization was attracting more and more attention. There are different methods and algorithms that can be grouped into deterministic and stochastic (Floudas, 2000) (Spall, 2003). Deterministic algorithms depend on the mathematical nature of the problem. The weaknesses of this technique are that it depends on the gradient, is likely to stagnate in optimal locations, and inefficiency in large-scale search spaces. Stochastic techniques are considered more user-friendly because they do not depend on the mathematical properties of a given function and are thus more appropriate for finding the optimal overall solutions for any type of function. As real-world optimization problems become increasingly complex, the use of stochastic methods becomes inevitable.
Genetic Algorithms (GAs) are adaptive methods that can be used to solve optimization search problems. They are based on the genetic process of living organisms. Genetic algorithms use heuristics for problem solving, which drastically limits the number of data to be used (Najarro, López, Racines, & Puris, 2017) (Rivero Peña, Novoa Hernández, & Fernández Ochoa, 2015). Algorithms with heuristic meta-heuristics are used to achieve optimal values in various areas of knowledge, in (Viera Carcache, Vinces Llaguno, Guerrero Goyes, & Marcillo Vera, 2017) the heuristic meta-heuristic Optimization based on Ant Cologne (ACO) is used for a mathematical model in applications in mobile phone systems.
Nature's ecosystems have always been a source of mechanisms for the inspiration and design of artificial computer systems for the solution of problems of considerable complexity in engineering and computer science. In the field of optimization, researchers have been inspired by biological processes to develop stochastic techniques that imitate the structures or behavior of certain creatures. As an example, genetic algorithms (GA), originally developed by (Holland, 1975), represent an exact abstraction of Darwin's model of evolution and biological genetics; ACO (ant colony optimization), proposed by (Dorigo, Maniezzo, & Colorni, 1996) ( Dorigo, Di Caro, & Gambardella, 1999), is based on the behaviour of forage ant colonies; PSO (particle swarm optimization), proposed by (Eberchart & Kennedy, 1995) and ( Chen, Zhu, Hu, & He, 2010), welcomes ideas inspired by the behaviour of flocks of birds and schools of fish. These algorithms have been developed to improve performance on classical heuristics or gradient-based methods, especially those functions that are undifferentiated, multimodal, and discrete. Today, these paradigms have been used in a wide range of areas.
In this paper, the biology and physics behind the chemotactic behavior (cell displacement induced by a substance) of the E. Coli bacterium is explained; then the algorithmic optimization model of the foraging behavior of the E. Coli is introduced; at the end a practical case study is shown where the algorithm can execute the optimization for a minimization problem given a benchmark function.
The Bacterial Foraging Optimization (BFO) algorithm (Muller, Marchetto, Airaghi, & Ko, 2002) is a new kind of global stochastic search technique biologically inspired by the clustering and displacement behavior of the E. Coli bacteria, which was introduced by (Passino, 2002), as well as similar ones based on collective swarms such as PSO and ACO, which have proven their effectiveness in this type of optimization. So far BFO has been successfully applied to several engineering problems, such as optimum control (Passino, 2002), harmonic estimation (Kim & Cho, 2005), reduction of transmission losses (Mishra, 2005), and automatic learning (Tripathy, Mishra, Lai, & Zhan, 2006).
In the same way that other algorithms mimic the behavior of animals in hunting, foraging, the strategy of searching for and grouping a swarm of E. coli bacteria in function optimization is the central idea of this relatively new algorithm.
2. Related Works
Researchers have developed dozens of optimization algorithms. Among these algorithms, some have gained significant acceptance in the research community. Such popular algorithms are taken into account in observations for experimental studies, one of which is the BFOA which is among the most popular metaheuristics under the swarm intelligence category (Salleh M.N.M. et al., 2018) analyzes the metaheuristics based on swarms within the intelligent social behaviors that occur in nature, focusing on the mechanisms of social interaction that maintain the balance between exploration and exploitation in an interval of iterations.
Heuristic algorithms reduce the effort, time, and errors of conventional methods, such as the trial-and-error method and the experience of the design method. In (Elsisi, 2019) (Zhou, Yang, & Wang, 2019) the performance of a proposed algorithm is compared with other well known algorithms through several Benchmark functions where it is stated that if the best solution with respect to the random initial is far from the optimal solution, the heuristic algorithm may take several iterations to reach the optimal solution.
In (Guang-Yu & Wei-Bo, 2017) the BFOA was compared using reference functions. The results obtained by the experiments indicate that the performance of the BFOA is among the six best algorithms in terms of the ability to converge to optimal or near-optimal solutions by applying the Ackley function, which is a multimodal function with many local optimals, and represents the most difficult class of problems for many optimization algorithms.
In (Yıldız & Altun, 2015) a comparative study of BFOA using numerical reference points is performed. Hybrid BFOA methods are proposed, improving the performance of the original algorithm. The Chemotaxis differential evolution optimization algorithm (CDEOA), which is based on two strategies, one of them makes the bacteria stronger and more exploitative, achieving that either of the two variants integrated into BFOA can improve performance in complex situations in fitness environments.
Within data mining in (Mahapatra & Banerjee, 2015) an object-oriented implementation of the Bacteria Foraging System (BFS) using BFOA is described, for the solution of data grouping problems. In data grouping, data is divided into significant groups called clusters without any prior knowledge, and is an important technique in a number of fields, which has been compared to several optimization algorithms such as the PSO.
In (Feng, He, Yang, & Juan, 2016) a variant to BFO is proposed using a new autoadaptable chemotaxis mechanism based on evolution strategies called ES-ABFO, based on the fact that each bacterium is looking for nutrient-rich areas; in fact, the chemotaxis process is an evolutionary progress, with this we look for the algorithm to maintain a better balance between a local search and a global search. Experiments are carried out to verify the reference functions and compare them with BFOA, PSO and other algorithms.
There are studies that improve the BFOA, in (Wang, Zhao, Tian, & Pan, 2018) and (Zhang, Chen, Luo, & Xu, 2018) variants are proposed in the original BFOA evaluating performance with well known numerical reference functions, being of great importance to promote research and improve the applications of the BFO algorithm.
3. BFO Algorithm
Bacteria grouping is an evolutionary algorithm which calculates the cost of the function after each iteration as the execution of the program progresses towards better fitness (optimal cost function).
3.1 Basic description of the BFO algorithm
The parameters to be optimized represent the coordinates (position in the plane) of the bacteria. The parameters are discrete within the desirable range, each set of these values representing a point in the coordinate space. Then a bacteria is positioned (created) at each point. As the iterations progress, the bacteria move to new positions (new coordinate values) and at each position the cost is calculated, and according to these values, the next movements of the bacteria are decided by the current gradient calculation, together with defined parameters. The aim of this is to bring the bacteria to the highest fitness position (optimal value).
The search and development strategy of the E.Coli bacteria is determined by four processes. These are chemotaxis, swarming, reproduction, and, elimination and dispersion. Chemotaxis is performed through swimming and tumbling (Floudas, 2000) (Biswas, Dasgupta, Das, & Abraham, 2007). When the bacterium finds a favourable environment (rich in nutrients and free from harmfulness) it continues to move in the same direction (swimming). The decrease in the cost function represents a favorable environment, while the increase in cost represents an unfavorable environment. When you encounter an unfavorable environment, the bacteria turn (tumbling) in other words, they change their direction. In swarming, bacteria move from their respective sites into cell groups.
3.2. Chemotaxis and Clustering
Chemotaxis simulates the movement of an E. coli by means of swimming and tumbling, the movements that allow it to carry out the scourges of the bacteria, cause it to advance or turn. Biologically this bacterium can move in two ways, it can swim and advance in the same direction for a period or it can turn in another direction, and alternate between these two modes of operation during its lifetime. Let's suppose that Ɵi(j,k,l) represents the i-th bacterium in its j-th chemothalamic step, k-th reproductive step and l-th elimination-dispersion step. C(i) is the measure of progress (step) in a random direction specified by the tumble. In this way the chemotherapeutic movement can be represented in a computational way by Eq. (1).
Where ∆ represents a random address vector whose elements belong to the range [-1, 1]. If the i-th bacteria finds a favorable medium, which represents less value in the cost function at a point in the coordinate space, then it is still swimming in the same direction it had in the previous chemotherapeutic step j-th. Otherwise, ∆ (i) is assigned a new value which is a random number within the range [-1, 1].
An interesting group behavior observed in some species of bacteria including E. Coli is swarming, in which through an intricate and stable set of spatio-temporal patterns (swarms), these are grouped together. A group of E. Coli join together to form a traveling ring which moves along the nutrient gradient, attracted by a chemo-efector of the nutrient substance. When stimulated by a high level of succinate (an enzyme component of cells), bacteria release an attractive aspartate, which helps them to form in groups and thus move in concentric swarms with a high density. Communication in these E. Coli swarms can be represented by function, Eq. 2. representing the swarming of E. coli bacteria.
Where  is the value of the target function, S is the population of bacteria, p is the number of variables to optimize, which is present in each bacterium and
is the value of the target function, S is the population of bacteria, p is the number of variables to optimize, which is present in each bacterium and  is a point in the p-dimensional search domain;
is a point in the p-dimensional search domain; 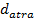 ,
,  ,
, 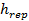 ,
, 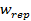 are coefficients that must be set appropriately (Floudas, 2000) (Passino, 2002).
are coefficients that must be set appropriately (Floudas, 2000) (Passino, 2002).
3.3 Reproduction
The health status (fitness) of each bacterium is calculated after each complete chemotherapeutic process. It is generally the sum of costs function 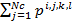 , where Nc is the total number of a complete chemotherapeutic process. Healthy bacterial locations represent the best set of optimization parameters. Then, to speed up and refine the search, more bacteria are required to be placed in the best locations that are achieved in the optimization domain, which is done in the reproduction process. Half of the healthiest bacteria survive (those with the lowest cost value of function), while the other half die. Each surviving bacteria divides in two, and is placed in the same location. In this way the population of bacteria remains constant.
, where Nc is the total number of a complete chemotherapeutic process. Healthy bacterial locations represent the best set of optimization parameters. Then, to speed up and refine the search, more bacteria are required to be placed in the best locations that are achieved in the optimization domain, which is done in the reproduction process. Half of the healthiest bacteria survive (those with the lowest cost value of function), while the other half die. Each surviving bacteria divides in two, and is placed in the same location. In this way the population of bacteria remains constant.
3.4 Disposal and Dispersion Event
The chemotherapeutic process performs a local search while reproduction accelerates the convergence of search parameters.
Although chemotaxis and reproduction may not be sufficient to reach the global minimum, because the bacteria may become stagnant in a local minimum, assuming that this is the best position in the surrounding area. To prevent this stagnation from happening, the elimination and dispersal event is applied. Those bacteria with a probability of elimination and dispersion are eliminated from the current location and randomly relocated in order to generate a global search, the population of bacteria remains constant.
4. Basic BFO Algorithm
Exposed the mathematical considerations of the simulation of the chemotherapeutic process, and the other processes that a bacterium E. coli performs when looking for food, the basic pseudocode of the BFO algorithm is exposed:
Parameters:
[Step 1] Initialize parameters p, S, N c , N s , N re , N ed , P ed , C(i)(i=1,2...S), Ɵ i .
Algorithm:
[Step 2] Control loop elimination - dispersion: l=l+1
[Step 3] Playback control loop: k=k+1
[Step 4] Chemotaxis control loop: j=j+1
[a] For i = 1,2,...S take a chemotherapeutic step for the bacteria i as follows:
[b] Calculate the fitness of the function, J(i, j, k, l).
Let J(i,j,k,l) = J(i,j,k,l) + J cc (Ɵ i (j,k,l),P(j,k,l)) (as an example, add the cell-to-cell attractiveness-repellent profile to simulate group behavior)
Where, J cc is defined as (2).
[c] Let J last = J(i,j,k,l) save this value as to find a better cost in an upcoming execution.
[d] Flip (tumble): generate a random vector 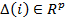 with each element ∆
m
(i), m = 1,2,...,p, a random number between[-1.1].
with each element ∆
m
(i), m = 1,2,...,p, a random number between[-1.1].
[e] Move: Do
Ɵ
i
(j+1,k,l) = Ɵ
i
(j,k,l) + C(i)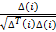
This result adds up a C(i) size step towards the direction in which the bacteria i turns.
[f] Calculate J(i, j+1,k,l) and compute
J(i,j+1,k,l)=J(i,j,k,l)+J cc (Ɵ i (j+1,k,l),P(j+1,k,l))
[g] Swimming (swim)
i) Set m=0 (counter for swimming distance)
ii) As long as m < N s (if not too low).
Set m=m+1.
If J(i,j+1,k,l) < J last (if it is better), do J last =J(i,j+1,k,l) and obtain
Ɵ
i
(j+1,k,l)= Ɵ
i
(j,1,k,l)+C(i)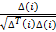
And use Ɵ i (j+1,j,k) to calculate the new J(i,j+1,k,l) as in the step [f].
Otherwise, do m=N s . This is the end of the loop while (ii).
[h] Go to the next bacteria (i+1) if i ≠ S (e.g. go to[b] to process the next bacteria).
[Step 5] If j < N c , go to[Step 4]. In this case, the chemotaxis continues as long as the bacteria is still alive.
[Step 6] Reproduction:
[a] For k and l , and for each i=1,2,...,S, Let the
Be it the health of the bacteria i (a measure of how many nutrients they possess during their lifetime and how satisfying it is to avoid harmful substances). Sort the parameters of bacteria and C(i) chemotaxis in ascending J health order (higher cost means lower health).
[b] The S r bacteria with the highest J health value die and the remaining bacteria in S r with the best values are divided (this process is executed by the copies being made and placed in the same positions as their parents).
[Step 7] If k < N re , go to [Step 3]. In this case, the specific number of playback steps has not been reached, so we start with the next generation of the chemotherapeutic loop.
[Step 8] Elimination - Dispersion: i=1,2,...,S with probability P ed , eliminate and disperse each bacterium (this keeps the number of bacteria in the population constant). To do this, if a bacterium is killed, it simply spreads a new one in a random location over the optimization domain. If l<N ed , then go to [Step 2]; otherwise terminate.
5. BFOA Analysis
The removal and dispersal operator is an essential link in BFOA.
5.1 BFOA Elimination and Dispersion interval analysis
With the probability of Ped, each bacterium is eliminated and dispersed in order to maintain a constant number in the population. If one bacterium is killed, another is randomly placed in another location within the optimization domain. The elimination and dispersion helps to escape those bacteria that are trapped in a local optimum. A higher probability of migration can help a bacterium to escape from a local optimum, but it also brings a problem called "leakage" that affects the speed of convergence and accuracy of the algorithm, and such a situation is not desirable.
For example, BFO is applied to solve a simple nonlinear function: z = (x-15)2+(y-15)2, where x ∈ [0,30], y ∈ [0,30]. Assuming a population of 10 bacteria, the number of generations is 4, the chemotherapeutic operator is executed 10 times in each generation, and the probability of elimination and dispersion is 20%, the individual trajectories of the bacteria are shown in Fig. 1. This function has an optimal solution in z = 0, where x=15 and y=15.
The origin shows the position of each bacterium, and the vectors show the change in the position of each bacterium, after a generation of optimization run. As shown in the figure, most bacteria are moving to the optimal position. Also, some bacteria marked with segmented lines near or above the optimum value suddenly move considerably away from the optimal value due to the removal and dispersal operation on the bacteria.
How can this be avoided? In the individual process of a bacterium, if the bacteria selected to apply the elimination and dispersal is at or near the overall optimum point, leakage will occur. Therefore, to prevent this from happening, such bacteria must be prevented from being selected. In addition, the removal and dispersal operator must be improved.
Additionally, individuals are sorted according to their current fitness level, the operator selects the individuals according to the P ed probability of the fitness values that are positioned behind the position according to the selection method used; while those in front will not be selected, because the individuals in front are in the overall optimal solution or very close to it. In this way, the individual's escape can be effectively prevented. As generations increase, individuals move closer to the optimal position. The proportion of removal and dispersion intervals should be reduced appropriately. Let Q be the percentage of removal and dispersion of the bacteria, and its initial value 1. The generation is the counter value of the chemotherapeutic generation, and its initial value is 0. A removal and dispersal cycle is performed every 10 generations of the algorithm, and the goal of removal and dispersal should be reduced every 20 generations. This means that if MOD 10 = 0 generation, then the removal and dispersion can be executed. Be it ged = generation DIV 20, Q = 1 - (2*ged*L), where L is the percentage of the initial value of the bacteria not involved in removal and dispersal. As generations increase, ged also increases, and the percentage of elimination and dispersion decreases. As a result we can say that the occurrence of the escape phenomenon can be avoided, and thus the speed of convergence can be improved considerably.
5.2 Chemotaxic interval analysis in BFOA
Chemotaxis is one of the most important actions at BFOA. During chemotaxis, bacteria are continuously swimming in search of the optimal solution to the problem. In the initial position, a bacterium turns over (tumbles) to take a random direction and then measures the feed concentration (measures the cost), then swims a fixed distance and then measures the concentration there again. This turning and swimming action constitutes a chemotacic interval, if the food concentration (higher fitness) is higher in the next location, the bacteria will advance in that direction again, otherwise if the concentration is reduced, the bacteria will then turn (tumble) to look for another direction to go (swimming). This process is carried out repeatedly, until maximum intervals are reached, which is limited by the lifetime of the bacteria.
In chemotaxis, the size of the interval is an important parameter, when the bacterium determines swimming in one direction (Biswas, Dasgupta, Das, & Abraham, 2007) ( Yao & Liu, 1998). How is the interval size determined? in conventional BFOA, a fixed interval size was selected based on experience. However, such consideration usually slows down the convergence speed of the algorithm. Thus, there should be better parameter values.
The selection of the interval size parameter is critical, through the algorithm design process. If the value is too small, the search will remain stagnant at a local optimum. On the other hand, if the value is too high, the search will lose the overall optimum.
6. Results
6.1 Proposal of the benchmark function, procedures and evaluation method.
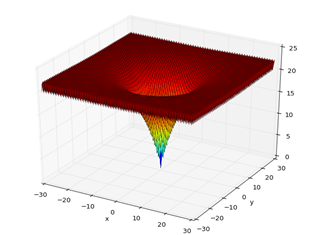
For the BFOA analysis, the resolution was applied to one of the benchmark functions, the Ackley minimization function, Fig. 2,
which has a global optimum, where xi=0 (i=1, 2, ..., n), and the optimum value is 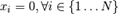 and the range
and the range 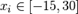 , is characterized by having many local optimals around the optimum point, and the possibility of maintaining a plateau state in the search for the global minimum.
, is characterized by having many local optimals around the optimum point, and the possibility of maintaining a plateau state in the search for the global minimum.
Resources.- Using a laptop computer (Pentium(R) dual-core processor at 2.30GHz, 4GB RAM memory) with Windows 7 operating system, the BFOA algorithm was implemented in the Python programming language, based on the basic algorithm proposed by the author of BFOA to evaluate the performance, three runs of the algorithm were applied for each change and/or modification of the parameters of BFOA, for each cycle were run 50 iterations of it. The best of each iteration is selected, and at the end the best overall, according to the literature proposed by the author of BFOA who proposes that the standard parameters are S=50, D=2, Nc=2, Ns=12, C=0.2, and Ped=1.15 as recommended in (Kim & Cho, 2005) ( Yao & Liu, 1998). After applying the author's default parameters, modifications were made to C and Ped, (varying them and checking their effect on the algorithm's behavior on the benchmark function). Once the cycles of iterations of the BFOA algorithm were executed, the values obtained were evaluated, minimum and maximum values obtained, mean of minimum values of each cycle, range, standard deviation, deviation among the three selected.
6.2 Analysis of results
Four tests were performed according to the changes in the parameters indicated in the analysis proposal. For each change in parameters, three iterations were performed: the minimum value of the three iterations was averaged, the standard mean of the minimum values in each iteration, the dispersion, and the standard deviation were calculated.
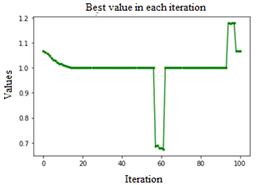
Ped =0.001, C=0.5, Fig. 3, stagnation was observed at local minima, as well as a constant oscillation of considerable amplitude, varying from minima to maxima quite frequently. Ped=0.001, C=0.8, Fig. 4, shows excessive variation between minimum and maximum values, is unreliable, and several runs are necessary to determine an average value for these values.
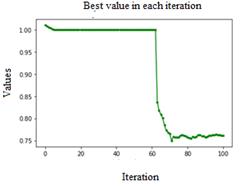
Ped=0.001, C=0.9, Fig. 5, an improvement in convergence towards an acceptable minimum was observed, from iteration number 30. Considerably acceptable, however, sometimes there is stagnation in the form of plateau, and after several more iterations, fall to an acceptable overall minimum, and return to maximum values.
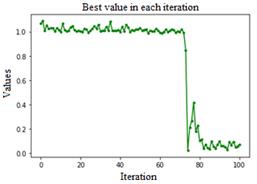
Ped=0.001, C=0.95, convergence is established, although plateau is still found between iterations twenty and forty, it is observed that more than one hundred consecutive iterations are needed to continue converging towards an acceptable global minimum.
Ped=0.001, C=1, plateau was observed from iteration ten to 80, in another execution plateau was observed in almost all iterations, sometimes reaching acceptable overall minimums but rising back to maximum values, convergence was also observed from iteration five and remains at minimum values below between 0 y 0.2.
Ped=0.1, C=1.10, Stagnation is observed from the initial iteration to the sixty, then it converges towards the global minimum 0, and it remained oscillating between 0 y 0.1.
Ped=0.001, C=1.10, showed stagnation from iteration twenty to seventy, and then converged towards global minimum before iteration one hundred.
Ped=0.2, C=1.15, Fig. 6, this configuration of the parameters is recommended by K. M. Passino, a constant oscillation is observed, converging towards global minimum after the seventy or eighty iterations, it reaches minimum value zero before the hundredth iteration.
Ped=0.01, C=1.3, Fig. 7, configuration proposed by the authors of this document, based on the observations and behaviour of the algorithm in previous configurations; immediate convergence was observed before iteration ten, and it was maintained at local minimums until an acceptable overall optimum minimum was reached.
Comparison of parameters C (turn size) and Ped (probability of elimination and dispersion)
The minimum value obtained for simulated environments is presented in Table 1, which compared with (Guang-Yu & Wei-Bo, 2017), (Yıldız & Altun, 2015) (Sharma & Kau, 2015), show that as long as C values are kept below 0.01, the algorithm is less susceptible to stagnation at a local minimum, it is observed that a value of 0.001 is adequate to accelerate the convergence of the algorithm. As for the values for the Ped parameter, it was observed that the values between 2 and 1 help the algorithm to escape from local minimums and stagnations, it was possible to appreciate peaks for both directions that reflect that when the algorithm stagnates, the parameter manages to take it out easily, although on rare occasions it could be appreciated that being in a global minimum, it can jump towards global maximums, so this value must be established objectively, because when there is no improvement in the solution this parameter makes it jump towards a random value according to the combination of parameters introduced, this parameter makes it jump towards a random value according to the combination of parameters introduced. With the values of Ped=0.01, C=1.3, an immediate convergence is achieved before iteration ten.
7. Conclusions and future work
In the present work we have experimented with the BFOA (bacteria foraging optimization) algorithm, which is inspired by the behavior of E. Coli bacteria, working in a group representing in a basic way how swarm intelligence behaves for the solution of optimization problems, in which optimal values are sought (minimum or maximum) on a specific function determined for real world problems, although it is true, the tests and measurements performed in this document were performed as tests and with a function that belongs to the benchmark group of optimization functions used to measure the effectiveness and development of an optimization algorithm, it is correct to apply this algorithm in the search for solutions to real-life problems, the important thing is to establish the objective function, and configure the parameters so that it is necessary to establish to what extent the algorithm can search for a desired solution.
With the analysis of the results of the tests carried out, the authors conclude that the parameters C and Ped play fundamental roles in the behaviour of the agents and the way in which they develop in order to search for local and global optimums. According to what has been observed, it is determined that C should be set at values lower than zero in order to have a favourable performance when it is stagnating in optimal locations, since it is the one that determines where and how much space it should turn in another direction and thus be able to escape from a local optimum. In the same way, the Ped parameter, which refers to the probability of executing the elimination and dispersion of a bacterium (search agent) when it is stagnant in a local optimum, or does not improve in values compared to its other search partners, this parameter is determined to be set between one and two, according to the need it has in the function to be optimized, this parameter is the one that together with the turning parameter, removes agents that are stagnant in optimal locations, or in plateau situation, removes them from the current position and takes them to new random positions according to the positions of the others, is basic and useful to escape from a very pronounced local optimum, behaves similar to the cooling and heating technique of the simulated annealing algorithm.
With the above it is concluded that the BFO algorithm can compete in effectiveness at the same level as PSO, BFO is recent and there is much to investigate and improve on this algorithm, it is possible to approach research and tests on mathematical analysis and how the parameters are related and how they can predict behavior according to the values that can be configured. At the same time present improvements in the algorithm, variants, and even be able to combine it with other collective intelligence algorithms.
Future studies could consider the application of this algorithm in real case studies, in the optimization of quality of service (QoS) in Manet (Mobile ad hoc network) type networks through routing protocols and consider parameters such as packet delay and minimum power consumption within the search algorithm configuration for the best possible route; in addition, the packet relay algorithm could be optimized in Adhoc networks based on collective intelligence (swarm intelligence), thus improving network performance and having low power consumption nodes.