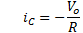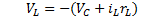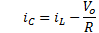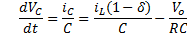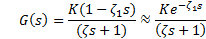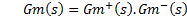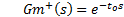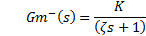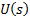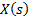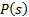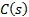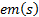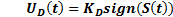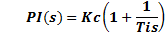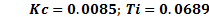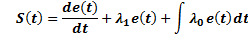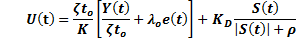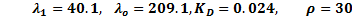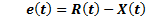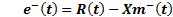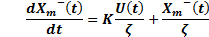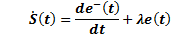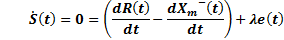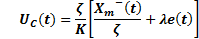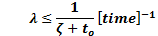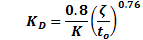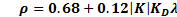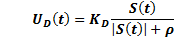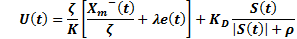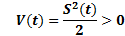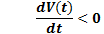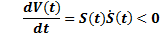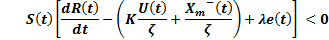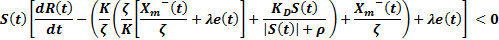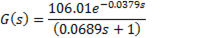1. Introduction
The Buck-Boost Converter (B-BC) is a DC / DC topology of power converters. DC-DC power converters are widely used in various applications such as in electrical power generation through photovoltaic systems, in DC energy storage systems, in DC power regulation systems, in photovoltaic power generation systems, aviation industry, aerospace technology and other fields (Rozanov, Ryvkin, Chavligin and Voronin, 2016).
A B-BC can be considered as a non-minimum phase system, which is characterized by the presence of a right-half plane (RHP) zero in the transfer function of system, when it receives the capacitance voltage as its output for feedback control. The ZRHP produces that the system operates in opposite direction during the initial transient response, affecting the dynamic response of the system. The non-minimum phase response of a Buck-Boost converter which works in Continuous Conduction Mode (CCM) is related to its inductance, load and duty ratio (Forouzesh M. et al 2017). Huang and Liu, (2016) present an analysis for non-minimum DC/DC converter. Internal model Control (IMC) has been used to eliminate problems originated by non-minimum phase behavior. Tarakanath, Pathwardan and Agarwal, (2014) present a study using IMC structure for Boost Converters. Other control structure is the sliding mode control (SMC). The design of SMC is attractive because it can deal with non-linear systems and exhibits robustness against modeling error and disturbances (Camacho and Lacruz, 2014). However, SMC can present a problem when it is used in the Buck-Boost causing chattering in the control action that is not ideal for the actuator, thus a hybrid approach (SMC-IMC) (Camacho, Smith and Moreno, 2003) can help in this sense.
This article shows the application of different control schemes to control a non-minimum phase Buck-Boost converter. Three control schemes are used. The first controller presented is a PI controller, the second one is Sliding Mode Control and the third one is a combination of two control schemes, Internal Model Control and Sliding Mode Control. The controllers are designed from a Right-Half Plane Zero (RHPZ) reduced order model. The RHPZ model is converted, using Taylor approximation, in a First Order Plus Dead Time (FOPDT) model and after that, the controllers are obtained. The performance of the SMC-IMC is compared against to a PI controller and a SMC. The simulation results show that SMC-IMC improves the converter response, reducing the chattering and presenting better robustness for load changes.
2. Fundamentals
2.1. Converter Description
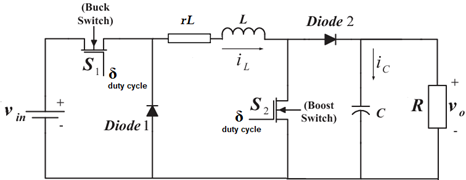
The topology of Buck-Boost converter is shown in Figure 1. This converter is a cascade connection of two basic converters: Buck converter and Boost converter. The notation used are: 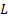 is the inductance,
is the inductance, 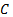 is the capacitance,
is the capacitance, 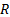 is the Resistance,
is the Resistance, 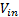 is the input voltage,
is the input voltage, 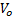 is the voltage in the load,
is the voltage in the load, 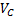 is the voltage in the capacitor,
is the voltage in the capacitor,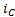 is the current in the capacitor,
is the current in the capacitor, 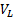 is the voltage in the inductor.
is the voltage in the inductor.
Switches S1 and S2 work simultaneously, i.e. they work with the same action control; modifying the duty cycle (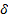 ) from 0 to 0.5 the converter works as Buck mode and from 0.5 to 1 it works as Boost mode. The variable to be controlled in the DC/DC converter is the output voltage in the load, the manipulated va56riable will be the duty cycle
) from 0 to 0.5 the converter works as Buck mode and from 0.5 to 1 it works as Boost mode. The variable to be controlled in the DC/DC converter is the output voltage in the load, the manipulated va56riable will be the duty cycle 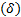 . The parameters used to analyze the Buck-Boost converter are shown in Table 1.
. The parameters used to analyze the Buck-Boost converter are shown in Table 1.
2.2. Modeling of converter
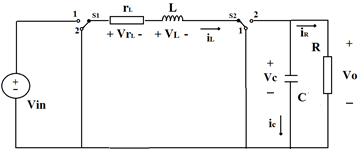
For modeling Buck-Boost converter two important conditions are considered. First, the converter works in continuous conduction mode and second is that the power semiconductor device work as an ideal switch, i.e. the semiconductor doesn’t dissipate power. Therefore, the input power is the same that the output power in the converter. The mathematical analysis of converter is carried out considering the switches S1, S2 in two positions (On/Off). The following equations are obtained from the Buck-Boost analysis scheme (Figure 2).
For the first case of analysis, switches S1 and S2 are in position 1, the converter response is described by Equation 1 and Equation 2.
For the second case of analysis, switches S1 and 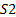 are in position 2, the converter response is described by Equation 3 and Equation 4
are in position 2, the converter response is described by Equation 3 and Equation 4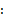
Combining Equation 1, Equation 2, Equation 3 and Equation 4 is obtained the dynamic behavior of Buck-Boost converter described by Equation 5 and Equation 6.
is obtained the dynamic behavior of Buck-Boost converter described by Equation 5 and Equation 6.
Analyzing Equation 5 in steady state 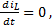 is obtained Equation 7.
is obtained Equation 7.
2.3. Linear Model Approximation
Buck-Boost converter is approximated to a linear model to facilitate the design of controllers. To obtain a linear approximation of the system, a reaction curve is applied to the converter because it has a first order dynamic behavior. The method used to approximate the model is the “First Order Plus Dead Time” (FOPDT) proposed by Smith and Corripio, 1997. Equation 8 represents the linear approximation of system. To use the approaches proposed by Camacho, Rojas and García, (1999) and Camacho, Smith and Moreno (2003), let us 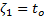 .
.
2.4. Control Schemes
Internal Model Control (IMC)
IMC is a control scheme used in systems with non-minimum phase dynamic. The presence of delay and RHP zero in the system can originate non-invertible controllers which are not possible to implement. Therefore, is necessary to eliminate delay and RHP zero of the control loop. IMC eliminates the non-invertible part of non-minimum phase systems of the control loop to get an implementable controller. The transfer function of system 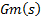 is separated in two parts to delete the control problems. The first part
is separated in two parts to delete the control problems. The first part 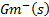 contains the invertible part of model and the second part
contains the invertible part of model and the second part 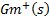 contains the non-invertible part of model. Below is shown the separation of model in Equation 9
contains the non-invertible part of model. Below is shown the separation of model in Equation 9
For the design of IMC, the FOPDT approach (Equation 8) is used; it presents a delay in the model of system, and generates a non-invertible controller. According to what was mentioned in Equation 9, it’s necessary to separate the non-invertible part of the model. The delay is separated from the transfer function of the system FOPDT and origins a transfer function as shown in Equation 10. The new transfer function of system without delay is shown in Equation 11 The IMC scheme is observed in Figure 3.
The IMC scheme is observed in Figure 3.
Where:
Sliding Mode Control (SMC)
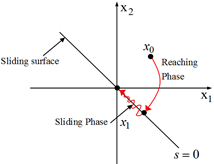
The idea of SMC is to define a surface with which the system can slide to its desired final value (Figure 4). The first step to design this controller is choose the sliding surface 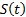 to define a global behavior for the system. The SMC control action
to define a global behavior for the system. The SMC control action 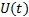 consists of two additive parts (Equation 12). The first part is called discontinuous action
consists of two additive parts (Equation 12). The first part is called discontinuous action 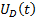 and it helps the system to reach the sliding surface. The second part is called continuous action
and it helps the system to reach the sliding surface. The second part is called continuous action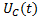 and it helps the system to stay on the sliding surface (Dominguez et al, 2016).
and it helps the system to stay on the sliding surface (Dominguez et al, 2016).
Sometimes, one problem that SMC presents is the chattering, this phenomenon consists in high-frequency oscillations around the value desired in the output of system. It happens when the discontinuous action reaches the sliding surface abruptly. Also, it causes that the control action damage to the actuator and appear unwanted dynamics in the system. Discontinuous control action 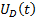 is based on Equation 13, the sign function is the discontinuous element.
is based on Equation 13, the sign function is the discontinuous element.
3.0 Design of Controllers
3.1 PI Controller
For tuning the PI controller (Equation 14), the FOPDT model of system (Equation 8) was used. The tuning method of Dahlin (Smith and Corripio, 1997) was considered.
Where:
3.2 SMC Controller
The method to design this controller was proposed by Camacho, Rojas and Garcia, (1999). It is a simple way of designing a SMC controller, and it can be generalized as a method of design for several processes. This last feature is the main difference with the original SMC (Tahri F., Tahri A. and Flazi, 2014), because the original procedure is based on a specific mathematic model of system and the design is exclusive for that system. For the design of SMC controller is used a linear approximation of the system FOPDT (Equation 8).
The design of SMC controller is shown in the work of Camacho, Garcia and Rojas, (1999). The sliding surface chosen in this work is presented in Equation 15.
The controller equation designed by Camacho is presented in Equation 16.
3.3 SMC-IMC Controller
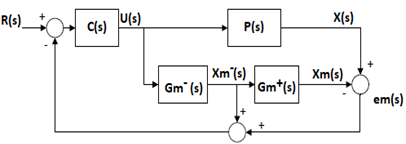
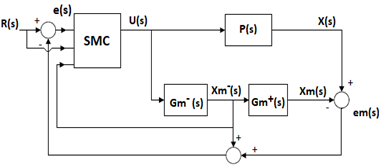
For the design of SMC-IMC controller, FOPDT approach model (Equation 8) is used. One problem of FOPDT approximation is the delay, to solve this problem the delay is eliminated of the control loop through the internal model structure. Therefore, the model of system without delay (Equation 11) is used to design this controller. SMC is added to the internal model scheme to improve the robustness of the system (Camacho, Smith and Moreno, 2003). Figure 5 shows the structure of SMC-IMC proposed in this work.
is used to design this controller. SMC is added to the internal model scheme to improve the robustness of the system (Camacho, Smith and Moreno, 2003). Figure 5 shows the structure of SMC-IMC proposed in this work.
Below, the design of SMC-IMC controller is presented. First, a sliding surface is chosen to define a global behavior for the system. The sliding surface chosen is shown in Equation 17.
Equation 18 represents the error of system.
Equation 19 represents the error of system considering it without delay.
The condition that must be met for the system to follow the reference and remain stable on the sliding surface is shown in Equation 20:
The continuous part  is designed below. The solution of the output of Equation 11 is presented in Equation 21.
is designed below. The solution of the output of Equation 11 is presented in Equation 21.
Considering Equation 20, the sliding surface (Equation 17) is derived.
Substituting Equation 19 into Equation 22, is obtained Equation 23:
Now replacing Equation 21 into Equation 23, is obtained Equation 24:
According by Camacho, Smith and Moreno, (2003), the tuning parameters are presented by Equation 25, 26 and 27:
The discontinuous part 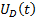 is based in Equation 13, the sign function is approximated as observed in Equation 28.
is based in Equation 13, the sign function is approximated as observed in Equation 28.
Adding Equation 26 and Equation 28 is obtained the control action (Equation 29).
The theory of Lyapunov is applied to analyze the stability of controller. Lyapunov’s function (Equation 30) chose is the sliding surface (Equation 17). Lyapunov’s condition is presented in Equation 31
Applying condition Equation 31 in Equation 30 is obtained Equation 32.
Replacing Equation 23 into Equation 32, results Equation 33.
Replacing Equation 21 into Equation 33, is obtained Equation 34:
Replacing Equation 29 into Equation 34, results Equation 35.
Solving Equation 35 is obtained the stability condition presented in Equation 36.
The parameters of 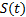 and
and 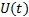 were tuned according to Equation 25, 26 and 27.
were tuned according to Equation 25, 26 and 27.
4. Simulation Results
Using the parameters of Table 1 and the model FOPDT (Equation 8), is obtained the transfer function (Equation 37), it is a linear approximation of Buck-Boost converter.
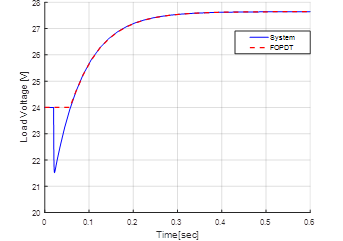
As shown in Figure 6 the FOPDT approximation does not consider the inverse peak in the response of Buck-Boost converter
Two tests are implemented to verify the performance of the proposed controllers. First, a step reference change around the operation point is applied in the converter. In the second test, the converter works on the operation point under load disturbances. The controllers are compared through performance indicators as ISE (Integral squared error), Ts (Stand Time), MPI (Undershoot).
4.1. Set-point step change result.
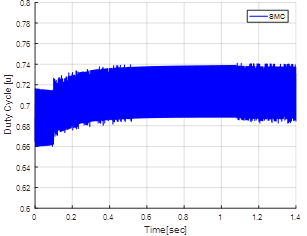
The variation of set-point is from 10 % with respect of the output as shown in the Figure 7 and Figure 8. The control action of SMC present chattering phenomenon as shown in Figure 7. Therefore, this controller is not recommendable to implement in this Buck-Boost converter.
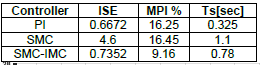
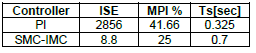
Below, there are the graphs corresponding to the simulation of the PI and SMC-IMC controller applied to the Buck-Boost converter. Table 2 shows the performance indicators to analyze the operation of the controllers.
4.2. Load Disturbances Changes
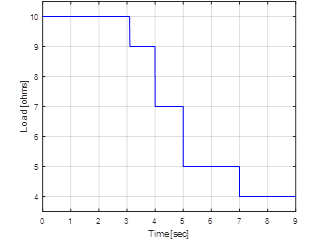
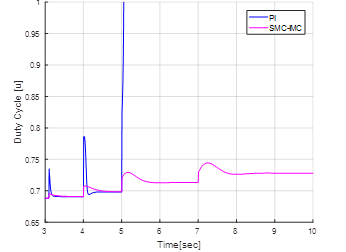
The Load Disturbances applied to the converter are variables with the time (Figure 9). The variation of the resistive load is from 10 % to 60 % respect the initial load, the response of converter is shown in Figure 10.
In Table 3 the parameters MPI %, Ts were obtained to the second disturbance, ISE parameter was obtained for all disturbances. ISE parameter of PI controller is very high because the system became unstable as shown in Figure 10.b.
5. Conclusions
Three controllers were evaluated to a non-minimum phase DC/DC converter.
Classical methods usually have not good performance when they are used for non-minimum phase electrical systems.
The application of SMC directly to non-minimum phase converters produce chattering to the final control element, which is not a desired condition.
The approach using SMC-IMC controller reduces the chattering phenomenon to a minimum and provides good performance and robustness for tracking and load changes.
The combination of classical control schemes plus robust methods is an alternative to continue experimenting.