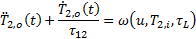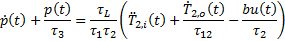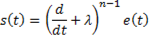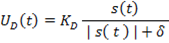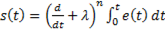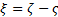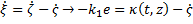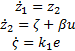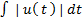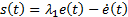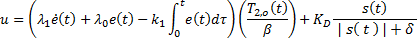1. Introducción
La industria requiere sistemas de control que proporcionen un rendimiento y robustez óptimos frente a perturbaciones o fallas del sistema y que sean fáciles de sintonizar por los operadores de plantas. Gran parte de los procesos en la industria presentan comportamientos complejos, retardos de tiempo y diferentes tipos de no linealidades, que pueden ser imposibles de superar con controladores convencionales como P, PI, PID, etc. Tal es el caso de los intercambiadores de calor que a pesar de que la transferencia de calor es típicamente eficiente, controlar la temperatura del fluido que se calienta en un punto de referencia específico y estable puede ser un desafío. Sin embargo, estos desafíos pueden ser superados aplicando técnicas de control no lineales. Es por ello, que para controlar este tipo de sistemas, se requieren esquemas de control robustos, siendo un enfoque concreto la metodología llamada Control por Modo Deslizante (Sliding Mode Control, SMC), la cual constituye un tipo particular de control por estructura variable, que se basa en el concepto de cambiar la estructura del controlador para cambiar el estado del sistema y obtener la salida deseada (Eker, 2006). Dado que el SMC tiene un procedimiento de diseño, es una de las más poderosas soluciones para muchos diseños prácticos del control (Utkin and Chang, 2002).
Este método de control no lineal, introducido por Emelyanov (1967), ha ganado significativamente valor con la tecnología de conmutación de rápido desarrollo y los trabajos de Utkin (1977, 1992); Utkin and Chang (2002), al ser aplicado comúnmente en muchos estudios en los últimos años (Yu and Kaynak, 2009). Un paso clave en el diseño de los controladores de modo deslizante es introducir una superficie deslizante adecuada para que los errores de seguimiento y las desviaciones de salida se reduzcan a un nivel satisfactorio (Slotine, 1984). En tal sentido, se ha intentado de varias formas establecer una técnica para el diseño de dicha superficie, pero los resultados muestran criterios que funcionan a manera de filtro para determinar si la superficie propuesta permite o no la estabilidad del sistema (Sira-Ramírez, 2015).
En (Pérez-Pirela et al., 2018) se desarrolló y validó un modelo dinámico para describir el comportamiento de un intercambiador de calor. Basados en este modelo, en el presente trabajo se diseñan dos algoritmos de control empleando la metodología de SMC convencional y a través de un análisis de comparación de índices de desempeño se selecciona el mejor para ser evaluada experimentalmente en un sistema real, para demostrar la aplicabilidad de esta técnica a un sistema práctico de intercambio de calor. Finalmente, los resultados obtenidos en las respuestas dinámicas del sistema de control real a lazo cerrado se comparan con las de simulación.
2. Metodología
2.1. Configuración experimental
Para la implementación y prueba de las estrategias de control basadas en el método de control por modos deslizantes se utiliza un intercambiador de calor a escala de laboratorio, como se muestra en la Figura 1. El sistema de intercambio de calor está compuesto por un calentador eléctrico de acero inoxidable con una longitud de 0.29 m, que contiene una resistencia eléctrica de 1000 W, los diámetros internos y externos son d1 =2" y d2 = 1", respectivamente, y el fluido entra con una temperatura T2,i (t) y pasa a través del calentador con un flujo volumétrico (F) de 2 L/min .
El objetivo de control es regular la temperatura de salida del fluido, 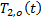 , manipulando la potencia suministrada por la resistencia eléctrica, mientras que las temperaturas iniciales (
, manipulando la potencia suministrada por la resistencia eléctrica, mientras que las temperaturas iniciales ( ,
, 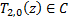 ) y la temperatura de entrada, T2,i (t) ϵ C2, son consideradas como perturbaciones. Las temperaturas del flujo de entrada y de salida son medidas con termopares tipo J. La potencia de la resistencia eléctrica es regulada con un relevador de bobina conectado a un dispositivo PWM. El flujo del fluido se controla con una válvula solenoide proporcional Asco® Posiflow® modelo SD8202G086V con una Unidad de control PWM marca Asco® modelo 8908A001 usando un lazo de control auxiliar que mide el caudal volumétrico con un sensor de flujo FLS® modelo ULF03.H.0. Todas las señales son leídas y manipuladas con un dispositivo Compact FieldPoint de Nacional Instruments®, operado por el usuario mediante una interfaz virtual desarrollada en LabView, que se ejecuta en un PC de escritorio que se comunica con el controlador vía Ethernet.
) y la temperatura de entrada, T2,i (t) ϵ C2, son consideradas como perturbaciones. Las temperaturas del flujo de entrada y de salida son medidas con termopares tipo J. La potencia de la resistencia eléctrica es regulada con un relevador de bobina conectado a un dispositivo PWM. El flujo del fluido se controla con una válvula solenoide proporcional Asco® Posiflow® modelo SD8202G086V con una Unidad de control PWM marca Asco® modelo 8908A001 usando un lazo de control auxiliar que mide el caudal volumétrico con un sensor de flujo FLS® modelo ULF03.H.0. Todas las señales son leídas y manipuladas con un dispositivo Compact FieldPoint de Nacional Instruments®, operado por el usuario mediante una interfaz virtual desarrollada en LabView, que se ejecuta en un PC de escritorio que se comunica con el controlador vía Ethernet.
2.2. Modelo del intercambiador de calor
Basándose en un modelo de parámetros distribuidos para el intercambiador de calor descrito en la sección anterior, Pérez-Pirela et al. (2018) desarrollaron un modelo matemático simplificado para este sistema, el cual describe el comportamiento dinámico de la temperatura a la salida (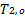 ), mediante una ecuación diferencial ordinaria de segundo orden (Ecuación 1) con retardo en la entrada (u), y las perturbaciones (
), mediante una ecuación diferencial ordinaria de segundo orden (Ecuación 1) con retardo en la entrada (u), y las perturbaciones (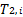 y
y 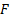 ),
),
donde
y 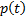 es una variable auxiliar cuya dinámica es,
es una variable auxiliar cuya dinámica es,
con condiciones iniciales  y
y  . Aquí,
. Aquí, 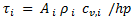 , para
, para 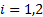 ; son los tiempos característicos de transporte de calor para cada material (resistencia
; son los tiempos característicos de transporte de calor para cada material (resistencia 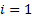 y fluido
y fluido 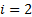 ),
), 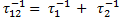 es el tiempo característico global,
es el tiempo característico global, 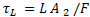 es el tiempo de residencia del fluido dentro del intercambiador,
es el tiempo de residencia del fluido dentro del intercambiador, 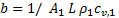 y
y 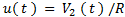 es la variable de control (para mayores detalles consultar (Pérez-Pirela et al., 2018)). Al ver la Ecuación es evidente que el grado relativo entre la entrada
es la variable de control (para mayores detalles consultar (Pérez-Pirela et al., 2018)). Al ver la Ecuación es evidente que el grado relativo entre la entrada 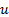 y la salida
y la salida 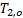 es dos.
es dos.
2.3. Algoritmo de control por modos deslizantes
Para fines de control se propuso el error de regulación 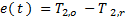 , donde
, donde 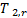 es la temperatura de referencia a la salida del intercambiador. El modelo para
es la temperatura de referencia a la salida del intercambiador. El modelo para 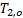 contiene incertidumbres paramétricas, por lo que para diseñar los controladores se aproximó la Ecuación 1 a la Ecuación 2,
contiene incertidumbres paramétricas, por lo que para diseñar los controladores se aproximó la Ecuación 1 a la Ecuación 2,
donde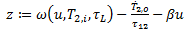 aglutina todas las incertidumbres.
aglutina todas las incertidumbres.
Para realizar las simulaciones y experimentos se emplearon dos técnicas de SMC con el propósito de regular el error 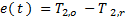 :
:
Técnica I: La primera técnica fue propuesta por (Utkin, 1992). La superficie de deslizamiento relacionada es la mostrada en la Ecuación 3,
con 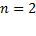 . La señal de control es la suma de la señal de conmutación y la señal de control equivalente. La señal de conmutación empleada es la descrita en la Ecuación 4.
. La señal de control es la suma de la señal de conmutación y la señal de control equivalente. La señal de conmutación empleada es la descrita en la Ecuación 4.
Técnica II: Ésta técnica se presentada para regular procesos químicos en (Camacho, 2000). La superficie deslizante es tomada de la Ecuación 5,
con 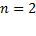 y la señal de control es la suma de la señal de conmutación y la señal de control equivalente. La señal de conmutación empleada es la descrita en la Ecuación 4.
y la señal de control es la suma de la señal de conmutación y la señal de control equivalente. La señal de conmutación empleada es la descrita en la Ecuación 4.
En ambas técnicas, 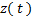 se estimó empleando un observador de alta ganancia, cuya dinámica total se puede escribir como se ve en la Ecuación 6.
se estimó empleando un observador de alta ganancia, cuya dinámica total se puede escribir como se ve en la Ecuación 6.
Una forma de estimar el término desconocido 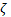 consiste en utilizar un observador. Para ello, se propone como error de estimación para
consiste en utilizar un observador. Para ello, se propone como error de estimación para 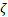 , según la Ecuación 7,
, según la Ecuación 7,
donde 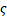 es el valor estimado de
es el valor estimado de 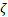 . La dinámica de
. La dinámica de 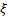 es descrita en la Ecuación 8.
es descrita en la Ecuación 8.
Como se usa un observador de alta ganancia, entonces 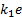 es mucho mayor a
es mucho mayor a  se puede despreciar, de tal forma que
se puede despreciar, de tal forma que 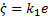 . Entonces el modelo en lazo abierto con la utilización del observador para determinar el término desconocido se ve en la Ecuación 9.
. Entonces el modelo en lazo abierto con la utilización del observador para determinar el término desconocido se ve en la Ecuación 9.
Se realizaron simulaciones y experimentos para el intercambiador de calor acoplado con cada controlador. La condición inicial del sistema, parte que el intercambiador de calor se encuentra en régimen permanente a una temperatura de equilibrio térmico de  , con un flujo volumétrico de
, con un flujo volumétrico de 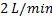 , una temperatura de entrada,
, una temperatura de entrada, 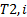 ; variable como perturbación de carga. A
; variable como perturbación de carga. A 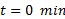 se arranca el controlador con una temperatura de referencia de
se arranca el controlador con una temperatura de referencia de  , luego a
, luego a 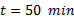 se la modifica a
se la modifica a 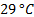 , para luego a
, para luego a 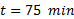 disminuir dicha temperatura a
disminuir dicha temperatura a 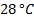 , con lo que se pretende medir las características de seguimiento a una referencia del sistema. Posteriormente, se disminuye el flujo volumétrico a
, con lo que se pretende medir las características de seguimiento a una referencia del sistema. Posteriormente, se disminuye el flujo volumétrico a 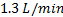 y se realizan de nuevo las pruebas comentadas anteriormente, con el fin de observar el comportamiento del sistema ante la variación en uno de sus parámetros nominales.
y se realizan de nuevo las pruebas comentadas anteriormente, con el fin de observar el comportamiento del sistema ante la variación en uno de sus parámetros nominales.
El rendimiento de las técnicas es evaluado con los siguientes índices:
La integral del absoluto del error (IAE por sus siglas en inglés) = 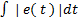
La integral del absoluto de la entrada de control (IACI por sus siglas en inglés) =
3. Resultados y Discusión
Los resultados de las simulaciones realizadas se presentan para demostrar el funcionamiento de las técnicas seleccionadas de SMC convencional. Estas simulaciones se implementaron en el entorno Matlab.
De la técnica I, se obtiene la superficie deslizante de la Ecuación 10,
y la entrada de control de la Ecuación 11.
Los parámetros empleados fueron 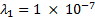
 ,
, 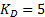 ,
, 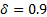 y
y 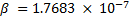 , los cuales fueron sintonizados manualmente.
, los cuales fueron sintonizados manualmente.
Del mismo modo, para la técnica II se consigue la superficie deslizante de la Ecuación 12,
y la entrada de control de la Ecuación 13.
Los parámetros empleados fueron 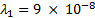
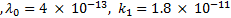 ,
, 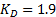 ,
,  y
y 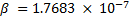 , los cuales fueron sintonizados manualmente.
, los cuales fueron sintonizados manualmente.
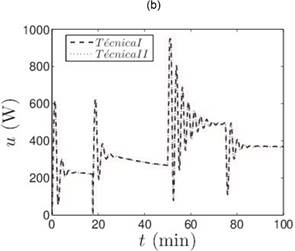
Para probar las propiedades de regulación del sistema, se aplicaron los cambios en la temperatura de referencia mencionados en la Subsección 2.3 y las respuestas se muestran en la Figura 2, para ambas técnicas. Como se observa en esta figura, ambas técnicas tienen un desempeño muy similar por lo que para determinar el mejor rendimiento, también se comparó con los índices de desempeño que son presentados en la Tabla 1. Estos resultados muestran que el sistema con el controlador de modo deslizante de la técnica II (Ecuación 13) tiene un mejor rendimiento que el sistema con el SMC de la técnica I (Ecuación 11).
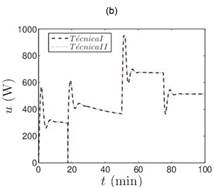
Para probar la robustez del sistema ante la variación de parámetros, se disminuye el flujo volumétrico a 1.3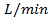 y los resultados son mostrados en la Figura 3. El rendimiento de las técnicas también se comparó con los índices de desempeño y son presentados en la Tabla 2. El sistema con los SMC convencional oscila durante la recuperación del disturbio, evidenciando que la técnica II nuevamente tiene mejor desempeño que la técnica I.
y los resultados son mostrados en la Figura 3. El rendimiento de las técnicas también se comparó con los índices de desempeño y son presentados en la Tabla 2. El sistema con los SMC convencional oscila durante la recuperación del disturbio, evidenciando que la técnica II nuevamente tiene mejor desempeño que la técnica I.
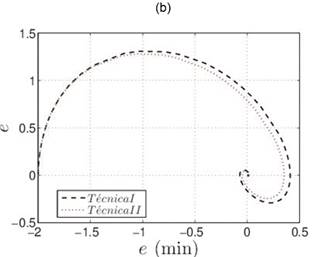
El objetivo del control por modos deslizantes es forzar tanto el error como la derivada del error al punto de equilibrio. Entonces la superficie deslizante seleccionada,  , tiende a cero en un tiempo finito y los estados del sistema deben permanecer en la superficie. En la Figura 4 se ilustran las superficies deslizantes de cada técnica, así como el error y la derivada del error. La variación en
, tiende a cero en un tiempo finito y los estados del sistema deben permanecer en la superficie. En la Figura 4 se ilustran las superficies deslizantes de cada técnica, así como el error y la derivada del error. La variación en  de la técnica I es más grande que la obtenida en la técnica II, es decir, la superficie deslizante de la técnica II converge más rápido. Adicionalmente, resulta interesante resaltar que el tiempo de alcance de ambas técnicas es muy similar y cuyo valor es cercano a 2.1
de la técnica I es más grande que la obtenida en la técnica II, es decir, la superficie deslizante de la técnica II converge más rápido. Adicionalmente, resulta interesante resaltar que el tiempo de alcance de ambas técnicas es muy similar y cuyo valor es cercano a 2.1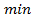 .
.
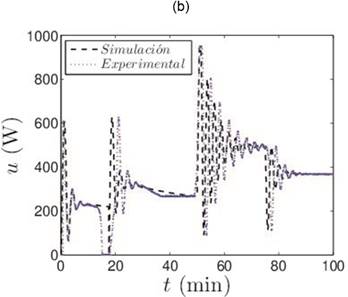
Al tener un mejor rendimiento la técnica II, se elige para validar los resultados teóricos con la aplicación real, como se muestra en la Figura 5. Se observa que en la respuesta dinámica del sistema en lazo cerrado, el sistema real y los resultados de simulación muestran un comportamiento muy similar. Y este resultado demuestra que el controlador diseñado lograr la tarea deseada con éxito.
4. Conclusiones y recomendaciones
En este estudio, se han aplicado técnicas de control de modo deslizante convencional a un sistema de intercambio de calor experimental para investigar la aplicabilidad de las técnicas propuestas. Se utilizó el modelo de parámetros distribuidos obtenido en (Pérez-Pirela et al., 2018). Se obtuvieron gráficas e índices de desempeño para la respuesta del sistema, señal de control y comportamiento de las superficies deslizantes que permitieron comparar las actuaciones de las técnicas. Durante las simulaciones y experimentos, los parámetros fueron afinados manualmente. Los resultados obtenidos de las simulaciones se compararon con los de la aplicación real para las respuestas dinámicas del sistema de control en lazo cerrado. Como resultado, el sistema real y los resultados de simulación mostraron un comportamiento muy similar. Los resultados experimentales aprueban que el controlador por modos deslizantes diseñado para el sistema de intercambio de calor; debido a la fácil aplicación, el algoritmo simple de la solución y la técnica robusta del control, se puede utilizar en usos industriales.