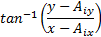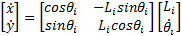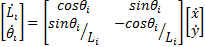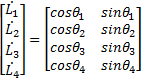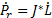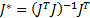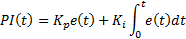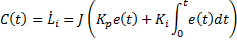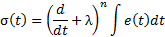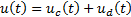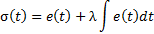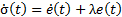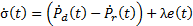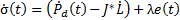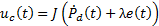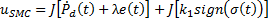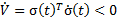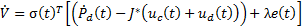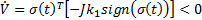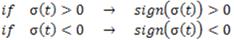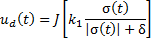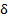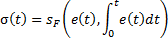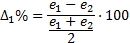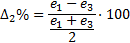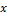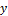1. Introduction
Robots have made formidable progress into industries for manufacturing and assembly. Traditional robots with serial or parallel structures are unsuitable since the workspace requirements are higher as in (Oh & Agrawal, 2003) are presented. For these motives, cable-driven mechanisms have received attention and have been recently studied. The advantages shown in (Zanotto, 2011), cables and tendon-like components in robotics have catched the interest of many researchers in the last years. Cable-direct-driven robots (CDDRs) are structurally similar to parallel robots (Jin et al., 2013) (Williams, Gallina, & Rossi, 2001) wherein the end-effector is supported in parallel by n cables with n tensioning motors. As compared to rigid links, cables are lighter and can handle larger loads guaranteeing considerable ranges of motion. However, one disadvantage is cables can only exert tension and cannot push on the end-effector. This property makes feedback control of CDDRs more defiant than conventional parallel robot as in (Babaghasabha, Khosravi, & Taghirad, 2014) is designed an adaptive controller in task space coordinates for a planar cable-driven parallel robot with uncertainties in dynamic and kinematic parameter or as in (Khosravi & Taghirad, 2014) a robust PID controller is presented for the cable-driven robot to ensure that all cables remain in tension. On the other hand, sliding mode control (SMC) is a nonlinear technique with robustness against the model uncertainties and ability of the disturbance rejection as in (Ataei & Shafiei, 2008) which introduced a SMC for a robot manipulator in order to deleting the oscillations of the response. Fuzzy control affords a methodology for representing, manipulating, and implementing a human’s heuristic knowledge about how to control a system. Fuzzy logic presents the ability to imitate the human mind to effectively occupy modes of reasoning that are approximate rather than exact. Designing of a Fuzzy Logic Controller (FLC) can show a lengthy process when performed heuristically (Nabi, 2013). FLC is identical to a conventional PID controller (Ghosh, Sen, & Dey, 2015). In case of FLC, control strategies are expressed in terms of fuzzy rules and this set of well-defined rules is known as fuzzy algorithm. Planar 4-Cable CDDR mode (Gallina, Rossi, & Williams II, 2001) is considered in this paper since no rotational move and no moment resistance are required on the end-effector, all 4 cables convene in a single point and the end-effector is modelled as a point mass. A Sliding Mode Control with a Fuzzy PI as sliding surface for the kinematic model of Planar 4-Cable CDDR is proposed. The performance of this controller is compared with a PI Controller and a conventional SMC in terms of integral square error (ISE) index. The simulation results show the ability the proposed controller in comparison with the conventional controllers for trajectory tracking and step change reference.
2. Methodology
2.1. Model of Planar 4-Cable Direct Driven Robot
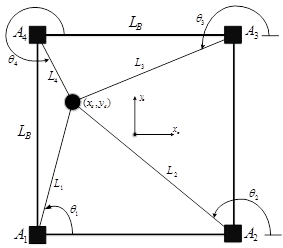
In this paper, we use only the reverse kinematic pose solution (Williams Ii & Gallina, 2003). Given the position 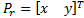 is found the cable lengths
is found the cable lengths 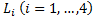 . The end-effector position
. The end-effector position 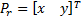 is possible to get by geometrical considerations (Euclidean Norm) with each fixed ground link vertex
is possible to get by geometrical considerations (Euclidean Norm) with each fixed ground link vertex 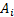 (Motor Position). In Figure 1 shows the Planar 4-Cable CDDR scheme. It is important to mention which each cable angle depend of quadrant.
(Motor Position). In Figure 1 shows the Planar 4-Cable CDDR scheme. It is important to mention which each cable angle depend of quadrant.
The reverse kinematics pose solution is given in Equation 1,
and the cable angles are given by Equation 2.
Considering the 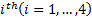 cable vector-loop closure equation
cable vector-loop closure equation 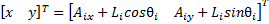 is calculated in the velocity kinematics Equations 3 and 4.
is calculated in the velocity kinematics Equations 3 and 4.
Inverting 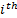 cable Jacobian matrix we have Equation 4.
cable Jacobian matrix we have Equation 4.
In order to build the inverse velocity solution of Planar 4-Cable CDDR (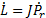 ) is necessary to eliminate the second row
) is necessary to eliminate the second row 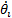 as (Williams Ii & Gallina, 2003) to relation the cable length rates and the end-effector velocity as shown in Equation 5.
as (Williams Ii & Gallina, 2003) to relation the cable length rates and the end-effector velocity as shown in Equation 5.
The alternate forward velocity solution with 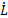 as inputs, is calculated through the left pseudoinverse Equation 6,
as inputs, is calculated through the left pseudoinverse Equation 6,
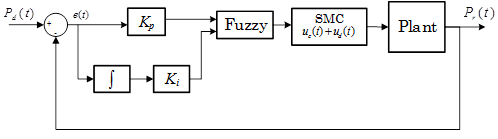
2.2. Design of controllers for Planar 4-Cable Cable Direct Driven Robot
This section designs different controllers for Planar 4-Cable (CDDR) based on the kinematic model. The designed controllers are a PI Controller, a conventional SMC and a Fuzzy Logic Controller.
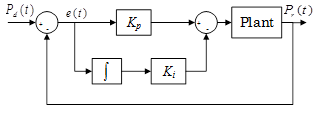
2.2.1. PI Controller
In order to design a PI controller, it is necessary to know the error. The control scheme of this controller is presented in Figure 2.
The tracking error vector is defined in Equation 7,
where  is the desired position vector and
is the desired position vector and 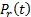 is the robot position vector.
is the robot position vector.
This controller has the form given in Equation 8.
Applying this controller to the kinematic model of Planar 4-Cable CDDR is necessary to multiply by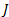 , getting
, getting 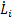 as control actions, as in Equation 9,
as control actions, as in Equation 9,
where 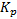 and
and  are tuning parameters. These parameters have been selected by trial and error until achieving the lowest ISE index.
are tuning parameters. These parameters have been selected by trial and error until achieving the lowest ISE index.
2.2.2. Sliding Mode Controller
This section shows the design of a SMC with a PI sliding surface (See Figure 3) from the kinematic model of Planar 4-Cable CDDR as in (Villacres, Herrera, Sotomayor, & Camacho, 2017) designs a conventional SMC with a PID sliding surface.
In order to design a conventional SMC, this sliding surface is considered as in Equation 10,
where 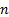 is the order of the system and
is the order of the system and 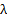 is a positive constant.
is a positive constant.
This controller has two components: a continuous 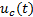 and a discontinuous
and a discontinuous 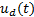 , shown in Equation 11.
, shown in Equation 11.
The system studied is the first order 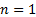 for this reason the derivative part of the surface is eliminated. The surface is expressed as in Equation 12.
for this reason the derivative part of the surface is eliminated. The surface is expressed as in Equation 12.
Now, the surface must be derived for the development of the controller (Equation 13).
By substituting Equation 7 in Equation 13 we have Equation 14.
By replacing Equation 6 in Equation 14, 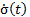 it can be rewritten as in Equation 15.
it can be rewritten as in Equation 15.
The continuous part of the controller is provided with the condition to keep the output on the sliding surface 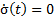 and considering the control law as
and considering the control law as 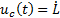 (Equation 16).
(Equation 16).
By completing the SMC control law, the discontinuous part 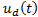 is added in Equation 17,
is added in Equation 17,
where 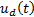 is responsible for reaching sliding surface and is composed of a non-linear function
is responsible for reaching sliding surface and is composed of a non-linear function 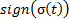 which switches about the sliding surface and
which switches about the sliding surface and 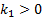 is a tuning parameter. These considerations were taken from (Herrera, 2017).
is a tuning parameter. These considerations were taken from (Herrera, 2017).
In order to design 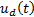 a positive-definite Lyapunov function
a positive-definite Lyapunov function  is defined in Equation 18.
is defined in Equation 18.
The derivative of the function  must be negative-definite (Equation 19).
must be negative-definite (Equation 19).
By replacing equation 15, 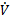 is as in Equation 20.
is as in Equation 20.
The control law is defined as and substituting we have Equation 21.
To satisfy Equation 19 and replacing Equation 16 in Equation 21, 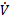 should be as in Equation 22,
should be as in Equation 22,
Therefore, by analyzing (Equation 23):
Finally, to reduce the chattering effect (Camacho & Smith, 2000), 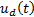 can be rewritten as a sigmoid function in Equation 24,
can be rewritten as a sigmoid function in Equation 24,
2.2.3. Fuzzy - Sliding Mode Controller
In this section, PI-Fuzzy sliding surface is proposed to a conventional SMC. The selection of this surface is based on the qualitative knowledge about the process to be controlled and was designed using Fuzzy logic toolbox in Matlab/Simulink. For the surface design, there are two inputs and one output. The surface is defined by Equation 25.
The control scheme of Fuzzy-SMC Controller is shown in Figure 4.
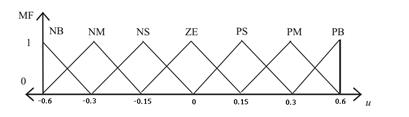
The Member Functions (MFs) are namely, NB (Negative Big), NM (Negative Medium), NS (Negative Small), ZE (Zero), PS (Positive Small), PM (Positive Medium), and PB (Positive Big) which are defined as symmetric triangles having 50% overlap. These MFs are shown in Figure 5. For the two input variables (error and integral error), the range for universe of discourse is [-2 2] and for the output variable (action control), it is defined in the range [-0.6 0.6] (Ghosh et al., 2015).
The selected rules for the sliding surface are listed in Table 1. The forty-nine fuzzy rules are based on sliding mode principle (Palm, 1992).
3. Simulation results
The controllers were implemented in Matlab/Simulink 2017a using the kinematic model of Planar 4-Cable CDDR. The tests were run on a computer with an Intel(R)Core(TM) i7-5500U CPU @ 2.40GHz with 8,00 GB RAM, running Windows 10. Figure 6 shows the simulator developed to observe the behavior of the cables during the trajectory. Two tests were performed:
Step Change Reference Test
Tracking Trajectory Test
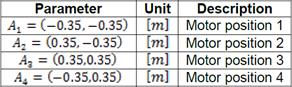
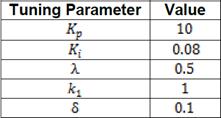
The simulation had a duration of 110 seconds with a sampling time of 0.1 for each test and uses ODE45 (Solve non-stiff differential equations). The physical parameters of Planar 4-Cable CDDR are presented in Table 2.
Finally, the values of 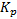 and
and  for PI Controller and
for PI Controller and 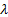 ,
,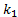 and
and 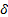 for SMC have been selected by trial and error until achieving the lowest ISE index. In Table 3 are shown these values.
for SMC have been selected by trial and error until achieving the lowest ISE index. In Table 3 are shown these values.
We used Equations 26 and 27 to compare the controllers based on ISE index. 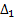 corresponds to the comparison between conventional SMC and Fuzzy-SMC Controller and
corresponds to the comparison between conventional SMC and Fuzzy-SMC Controller and 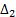 corresponds to the comparison between PI Controller and the control law proposed,
corresponds to the comparison between PI Controller and the control law proposed,
where 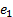 ,
, 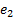 and
and  represent error values for Fuzzy-SMC Controller, PI Controller and conventional SMC respectively.
represent error values for Fuzzy-SMC Controller, PI Controller and conventional SMC respectively.
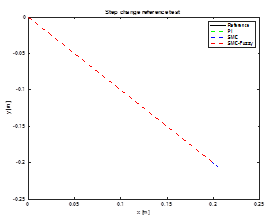
3.1. Step change reference test
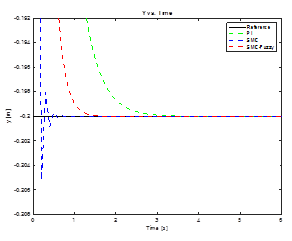
In this test, a step change reference is made from the reference  to the point
to the point 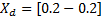 . In Figure 6 illustrates the end-effector path.
. In Figure 6 illustrates the end-effector path.
Figure 7 presents 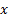 and
and 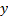 end-effector positions during the change reference to the position
end-effector positions during the change reference to the position 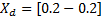 . The percentage overshoot of Fuzzy-SMC Controller is less than conventional SMC and the setting time is lower than PI Controller.
. The percentage overshoot of Fuzzy-SMC Controller is less than conventional SMC and the setting time is lower than PI Controller.
In Table 4 shows ISE index comparison between three controllers for step change reference test wherein the performance of Fuzzy-SMC Controller is the best according to ISE index.
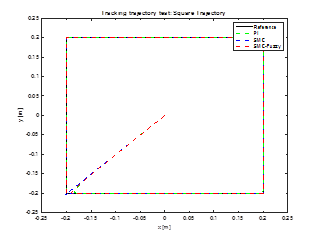
3.2. Tracking trajectory test: square
In this test, the selected trajectory is a square whose side length is 0,4[m]. In Figure 8 illustrates the efficiency of three designed controllers for this desired trajectory.
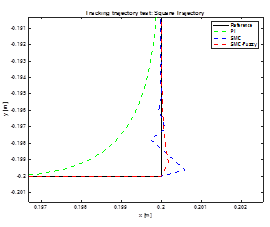
In Figure 9 presents an image zoom at beginning and at the corner of the square trajectory, which shows Fuzzy-SMC Controller has lower overshoot than conventional SMC.
In Table 5 shows the ISE comparison between the three controllers for tracking trajectory test.
In all tests, the proposed control law presents the lowest ISE index compared to the two controllers, the first is a PI controller and the other is a conventional SMC controller. In the two tests performed, the movement of the end effector is significantly improved because the fuzzy controller applied to the sliding surface softens the control actions, which are abrupt of the SMC controller.
4. Conclusion
In this paper, PI, SMC and Fuzzy-SMC controllers were designed for end-effector position control of Planar 4-Cable CDDR based on the kinematic model. These controllers were able to perform trajectory tracking and step change reference wherein the results indicate which SMC with Fuzzy-PI as sliding surface with forty-nine rules presents lower setting time than PI controller and lower oscillation than the conventional SMC. The performance of the controller was evaluated in terms of integral square error (ISE) index and these results demonstrate the effectiveness of proposed controller showing an acceptable accuracy.