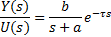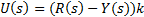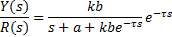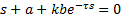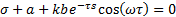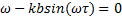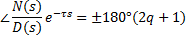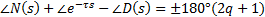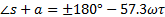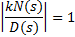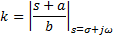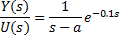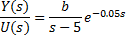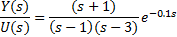1. Introduction
Time delays appearing in the modeling of different classes of systems (chemical processes, manufacturing chains, economy, etc.), become a challenging situation from a control viewpoint that should be affronted to yield acceptable closed-loop stability and performance. Several control strategies as well as stability analysis have been developed to deal with time delays. When the continuous case is considered, the delay operator can be approximated by means of a Taylor or Padé series expansions which could leads to a non-minimum-phase process with rational transfer function representation (Gouaisbaut, 2006). With the same stability purpose analysis, some works have applied the Rekasius substitution; see for instance (Munz, 2009). It should be noticed that using the mentioned strategies and if a closed-loop stability analysis is desirable, the stability results obtained are limited due to the corresponding approximations.
On the other hand, (Silva & Bhattacharyya, 2005) provided a complete parametrization of the stabilizing P, PI and PID controllers in the case of first order system plus time-delay (FOPTD) by using a frequency approach analysis. It is important to mention that the used stability analysis is not easy to extend to high order systems due to the fact that many stability conditions should be satisfied and in some cases the problem turns to determine the most relevant stability condition. Even with this disadvantage in (Silva & Bhattacharyya, 2005), the stability conditions for FOPTD systems are obtained when P, PI and PID controllers are regarded.
The root-locus method has been used as invaluable design tool for linear systems (Suh & Bien, 1982). This is because closed-loop stability can be assured from the obtained root-locus diagram. Root-locus graphical method is a method that allows to analyse how the roots change when the variation of a parameter is regarded. This method has been used in order to establish closed-loop stability conditions and therefore the design of some controllers can be addressed by analysing the obtained graphic.
Generally, it is not easy to analyze the stability of time-delay systems, especially when the systems are of high order or they have multiple delays. In (Wang & Hu, 2008), the concept of rightmost characteristic root is used as the root with the maximal real part of the characteristic roots of a time-delay system. For retarded time-delay systems, the stability can be determined by the rightmost characteristic root (Wang & Hu, 2008). In this way, in (Wang & Hu, 2008), the computation of the rightmost characteristic root of time-delay systems is addressed, on the basis of the Lambert W function. It can be seen that using this approach is not possible to obtain information of the complete number of poles, however the method presents some advantages from analytical viewpoint.
In (Banker, 2011) the authors provide the tuning of PID controllers for delayed FOPTD plants using the root locus, solving the problem by the evaluation of the phase condition and magnitude condition. The authors present the idea of the used computational functions, however there is not available the developed software.
Moreover, in (Banker, 2011) the case of high order system is not solved, neither plants with many zeros. Inspired in the proposal presented in (Banker, 2011), the main idea of this work is to design a software platform that allows the user to obtain the root-locus diagram for delayed systems, even when the user does not know the details of the program. This, with the idea of provide a similar Matlab rlocus() tool for finite dimensional linear systems. In this manuscript the progress of the computational development and analysis is presented to the cases FOPTD and second order plus time-delay (SOPTD) systems.
This manuscript is organized as follows, the problem formulation is presented in Section 2. Then, in Section 3 the computation of the root locus is depicted. Some examples are stated in Section 4 and finally in Section 5 some conclusions are provided.
2. Problem Formulation
In order to illustrate the troubles that arises when the computation of the closed-loop roots is desirable, let us consider the simplest delayed case. Consider a FOPTD system given by Equation 1,
where the parameters a,b and τ are known, τ is the time-delay associated to the transfer function; and a proportional control given by Equation 2,
where R(s) is the reference input. In such case, the closed-loop transfer function is as in Equation 3,
With a, b and τ as known constants. τ is the time-delay associated to the plant (Equation 1). If an analysis of the root-locus is applied to Equation 4, some problems could appear and the root-locus diagram could not be easily performed. In this section it is illustrated some typical troubles associated to the root-locus for delayed systems. As a first attempt to solve our problem, a simplified problem could be formulated as follows: for a given constant gain k, find all the roots of Equation 4. Under this conditions, the nature of the roots of Equation 4 is analysed. The roots of the Equation 4 are all the values of the complex variable 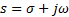 such that Equation 4 is satisfied, from this viewpoint we have two unknown parameters to be obtained. Then, taking into account the Euler identity, the closed-loop characteristic equation can be rewritten as in Equation 5.
such that Equation 4 is satisfied, from this viewpoint we have two unknown parameters to be obtained. Then, taking into account the Euler identity, the closed-loop characteristic equation can be rewritten as in Equation 5.
The solution of Equation 5 can be obtained by considering the following nonlinear system in Equations 6 and 7.
To solve the nonlinear system equations it is required to obtain the values σ and ω such that the Equations 6 and 7 are satisfied for a given k. Thus, a nonlinear system equations with two equations and two unknown variables (σ and ω) is obtained, which has not in general an analytical solution. Moreover, since the functions sine and cosine are involved, the system equations has an infinite number of solutions. If a numerical iterative solution is designed to the nonlinear Equations 6 and 7, for the first iteration an initial value for the algorithm should be proposed and this gives as a result one solution σ, ω. For the second iteration, an initial value should be asked and there is not way to assure that the proposed initial value gives a different solution that the one found in the first iteration. Therefore a bad selection of the initial value to the algorithm, give as result an unnecessary spent of time. Also, taking into account that the system equations has an infinite number of solutions, the task of obtaining all the roots (Equation 5) will be not possible.
The solution of the Equation 5 is not an easy task, even when some lines above, the problem has been simplified and formulated when the parameter k is fix. In order to obtain a root-locus diagram it is required to obtain the roots of Equation 5 for different values of k.
In the next section a computational solution to obtain a root-locus for delayed systems is used. This solution is based on the phase and magnitude conditions of the system. The method is not it has not been exploited to high order delayed systems, neither it has been presented as a finished Matlab function in order to use it as a control design tool.
3. Root-Locus Computation
The main idea behind to building the root-locus diagram for delayed systems is based on the fact that the phase condition of the system 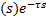 , given by Equation 8.
, given by Equation 8.
For q=0, 1, 2, …, is always satisfied for the roots of the closed-loop system. Therefore, the phase is tested for a known region of the plane s. The iterative proposed algorithm consists in selecting a point in the plane 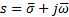 where
where 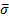 and
and 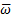 are given. Then, left side of the Equation 8 is evaluated and it is verified if the Equation 8 is satisfied. If Equation 8 is satisfied, then it is concluded that the root
are given. Then, left side of the Equation 8 is evaluated and it is verified if the Equation 8 is satisfied. If Equation 8 is satisfied, then it is concluded that the root 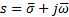 associated to the given
associated to the given 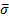 and
and 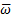 is a root of the characteristic equation, and this values are kept to use it later, if the condition (Equation 8) is not satisfied then the values
is a root of the characteristic equation, and this values are kept to use it later, if the condition (Equation 8) is not satisfied then the values 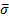 and
and 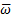 are not kept. After this, a second point in plane s, is selected and the method is applied again. Since a computational program is used to evaluate the condition (Equation 8) it is important to establish a tolerance in the right side of condition (Equation 8), in such case the program should evaluate strictly as in Equation 9.
are not kept. After this, a second point in plane s, is selected and the method is applied again. Since a computational program is used to evaluate the condition (Equation 8) it is important to establish a tolerance in the right side of condition (Equation 8), in such case the program should evaluate strictly as in Equation 9.
Another issue, is the number of points evaluated in the algorithm. In our experience this is a parameter that should be selected by the user due to the velocity of the complete computation depends directly from this parameter. Thus, if a quick idea of the root-locus is required, the user can select a small number of points.
In order to provide some comments on the phase system, consider a FOPTD system given by Equation 1. For this case, Equation 8 is given as in Equations 10-13
It can be seen, the phase contribution of the delay term is 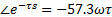 , the phase contribution of the stable pole depends on the position of the given proposed point
, the phase contribution of the stable pole depends on the position of the given proposed point 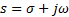 and it is easily calculated using some facts on the right-triangle. In the case of FOPTD system, the phase contribution calculation of the stable pole
and it is easily calculated using some facts on the right-triangle. In the case of FOPTD system, the phase contribution calculation of the stable pole 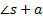 , four different cases are derived: two cases when the point is at right of the stable pole, and two more when the point is at left of the stable pole, see Figure 1. For the case of SOPTD or higher order plants without zeros, the contribution of the poles should be done carefully, because the calculation of such contributions derive on more than four cases as it was illustrated for the FOPTD system. It is important to highlight that the open-loop phase testing does not depends on the gain of the controller k, and this can be seen as an advantage of the method due to in the problem formulation section it was illustrated that in the original problem the variable k complicates considerably the problem statement analysis.
, four different cases are derived: two cases when the point is at right of the stable pole, and two more when the point is at left of the stable pole, see Figure 1. For the case of SOPTD or higher order plants without zeros, the contribution of the poles should be done carefully, because the calculation of such contributions derive on more than four cases as it was illustrated for the FOPTD system. It is important to highlight that the open-loop phase testing does not depends on the gain of the controller k, and this can be seen as an advantage of the method due to in the problem formulation section it was illustrated that in the original problem the variable k complicates considerably the problem statement analysis.
Once that a desirable region of the plane s is swept by testing the phase condition (8) and the roots of the characteristic equation has been detected, the next step is to obtain the gain k associated to each root. In order to compute the gain k the magnitude condition is used (Equation 14),
in the case of the FOPTD system previously analyzed (Equation 15).
Finally, in order to perform the root-locus diagram, the roots obtained from the phase condition test are plotted, also taking into account the corresponding proportional gain k. The roots are plot depending on the value of k, for instance the roots color red are the roots obtained with the interval 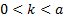 , then the roots color yellow are the roots obtained with the interval
, then the roots color yellow are the roots obtained with the interval  , after this, the roots color blue are the roots obtained with the interval
, after this, the roots color blue are the roots obtained with the interval 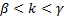 , with
, with 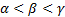 , and so on.
, and so on.
4. Results
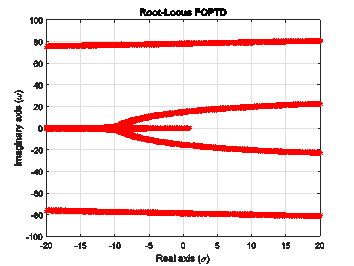
4.1 Example 1. Consider an unstable FOPTD system given by Equation 16.
Thus, the developed computational method should find the values satisfying the phase condition (Equation 8). Figure 2 shows the plot of the points satisfying that condition and therefore it is concluded that these points are root-locus. Now, the value of the proportional gains is required in order to interpret the closed-loop stability.
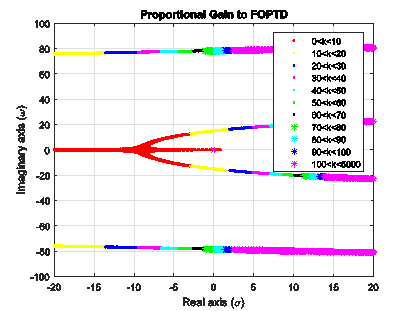
In this way, by applying the magnitude condition (Equation 14), the values of proportional gains k associated to each point found were obtained. In Figure 3, the root locus diagram with intervals of values k is shown. This intervals allows to have an idea of the performance of pole in close-loop for variation of the parameter k, and also allows to obtain the stabilizing gains of proportional controller, k. Note that roots with red color belong to the interval 0<k<10, and the roots color yellow belong to the interval 10<k<20. With a careful analysis of the root-locus diagram shown in Figure 3, the stabilizing interval is 1<k<15.
4.2 Example 2. Consider a new FOPDT unstable system, as in Equation 17.
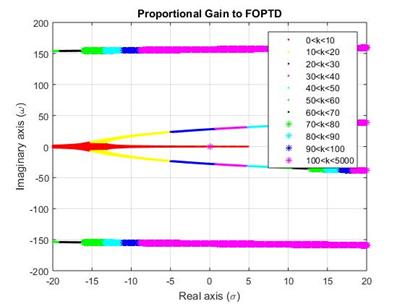
In Figure 4, the corresponding root-locus diagram is presented and the interval of proportional control that stabilize the studied system is 2<k<28.
4.3 Example 3. Consider a SOPDT unstable system, shown in Equation 18.
In Figure 5 is the obtained root-locus diagram using the depicted algorithm, and the intervals of k are stated by different colors. In this case, the stabilizing interval of proportional control is 3<k<20.
4.4 Example 4. In this example, an unstable SOPTD with one zero is considered (Equation 19).
For this case, in Figure 6 the associated root-locus diagram is presented.
In Figure 6 are shown the intervals of k. For closed-loop stability it is required that all roots are in the left half plane (LHP). Therefore, for this case a stabilizing proportional controller is given by 5<k<11.
5. Conclusions
In this work it is illustrated the computational issues that should be taken into account in order to perform a root-locus diagram for delayed systems. The simplest cases FOPTD and SOPTD systems are considered. This computational method plots a root-locus diagram of FOPTD and SOPTD systems to can analyze them. In the computational program, the values a, b and τ could be changed to obtain the root-locus diagram of FOPTD and SOPTD. On the other hand, the authors propose as a future work the generalization of the computational method for delayed systems with any number of poles and zeros. The main objective of this developments is to design an interface to obtain root-locus of delayed systems as a future work. In the present manuscript the essential ideas has been stated as well as the possible future problems when the generalization is considered.