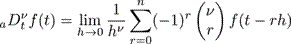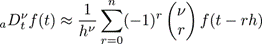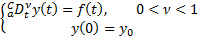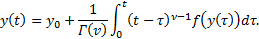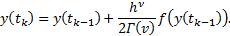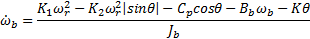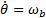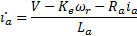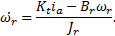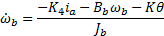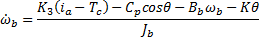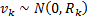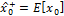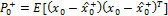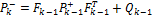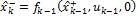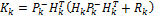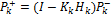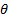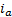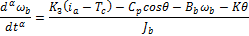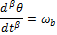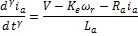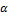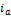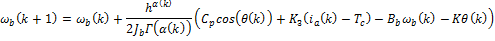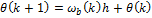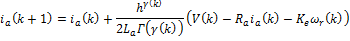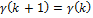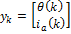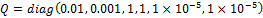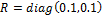1. Introduction
Fractional calculus is a field of mathematical analysis in which integro-differential operators of arbitrary order have an essential role; this field goes back to the times of Leibniz, around 1695, but in the last few decades it has become a very active research topic. Some of the current applications are in viscoelastic materials, heat transfer and diffusion, wave propagation, electrical circuits, electromagnetic theory, modeling and control of dynamical systems to mention only a few (Miller and Ross, 1993; Tenreiro et al., 2010; Rahimy, 2010).
This research focuses on the modeling of electromechanical systems by fractional derivatives. It is motivated and somewhat related to the works by several authors, namely:
(Gómez et al., 2016): The authors present an analytical and numerical study of the differential equations for an RLC electric circuits dynamical model by fractional derivatives. The considered system does not include mechanical components and there are no actual measurements.
(Chen et al., 2017): This reference introduces a design for DC-DC converters based on fractional order derivatives. There are comparisons with actual frequency measurements.
(Schäfer and Krüger, 2006): The behavior of an iron core with saturation is evaluated based on changes in the frequency of the electromagnetic field, behavioral data is saved and used to design a fractional core circuit model. Although in this study actual measurements are used, there are no mechanical components in the system and the fractional parameters are not fully explained.
(Özkan, 2014) and (Swain et al., 2017): These references propose fractional PID controls for electromechanical systems with integer order models. As proposed by (Podlubny, 1999), it is important to look for an alternative fractional derivatives model, since the proposed controls exhibit poor performance.
(Lazarevi et al., 2016) and (Petrás, 2011): They show the direct relationship between modeling based on fractional derivatives and duality mechanical-electrical of electromechanical systems. The model identification is made in frequency domain.
The aim of this paper is the modeling of a dynamical electromechanical system by fractional differential equations. Furthermore, the fractional orders of the derivatives are optimal and are estimated by an extended Kalman filter (EKF), based on actual time measurements. As far as we know, this approach is new and worthy.
The paper is organized as follows: Section 2 introduces the fractional derivatives by Grünwald-Letnikov and Caputo, the dynamical models for a VTOL electromechanical system and the EKF estimation procedure. The numerical results are the subject of Section 3 and Section 4 is devoted to the conclusions.
2. Methodology
Firstly, we introduce the fractional order derivatives in the sense of Grünwald-Letnikov and Caputo. Subsequently we consider the mathematical model for the VTOL electromechanical system and the method of parameter estimation known as extended Kalman filter.
2.1 Definitions of fractional order derivatives
In the development of the fractional calculus several definitions for the arbitrary order derivatives and integrals have appeared. The best known are: the Grünwald-Letnikov (GL), the Caputo (C) and the Riemann-Liouville (RL) definitions. The first two are the ones implemented in this work (Podlubny, 1998).
2.1.1 Grünwald - Letnikov derivative
Let  . The Grünwald-Letnikov fractional derivative of order ν of a real function f is basically an extension of the backward finite difference formula (Swain et al., 2017). It is given by
. The Grünwald-Letnikov fractional derivative of order ν of a real function f is basically an extension of the backward finite difference formula (Swain et al., 2017). It is given by
where nh = t - a.
This definition can be easily approximated by taking a discretization parameter h small enough. The numerical approximation is given by
where m - 1 < ν < m.
2.1.2 Caputo derivative
Let 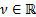 . The Caputo fractional derivative of order ν of a real function f is given by
. The Caputo fractional derivative of order ν of a real function f is given by
where m - 1 < ν < m.
As stated in (Li and Ma, 2013) and (Podlubny, 1998) the Caputo initial value problem
is equivalent to the Volterra integral equation of the second kind, given by
The Caputo derivative can be approximated by a quadrature rule like a trapezoidal rule, i.e.
Now we proceed to the modeling phase of our work.
2.2 Modeling of an electromechanical system
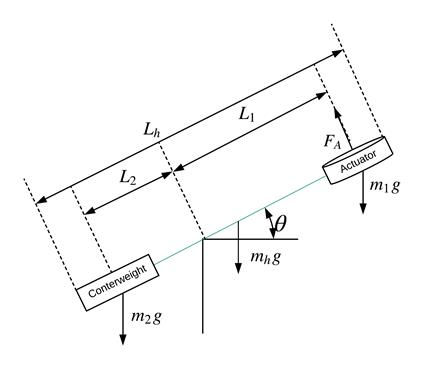
A Qnet vertical take-off and landing (VTOL) is the electromechanical system considered here. This system consists on a speed fan with helices (motor actuator) adjusted to a fixed base by one arm and a counterweight on the other side as it is shown in Figure 1. The air flow through the propellers affects the dynamics of the system, and changes the angular position of the weight by the rotation of the arm around the pivot. Some applications of this system in real world devices are helicopters, rockets, balloons, and harrier jets (Apkarian et al., 2011).
2.2.1 Physics of the system
The mechanical, electrical and aerodynamic laws that explain the behavior of the system, allow us to characterize the nonlinear dynamical model of the system by the following set of equations:
This set of equations is denoted (NLS). In search of a nearby simpler set of equations, (Apkarian et al., 2011) propose a simplification for the first and the third equations given by
The modification of the first equation corresponds to the replacement of the thrust 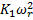 and the drag
and the drag 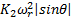 by the standard torque motor relation
by the standard torque motor relation  .
.
Based on this work, we propose a simplified system of equations which is nonlinear. It maintains the gravitational torque 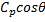 in the first equation and takes into account the counter-electromotive torque in the arm and rotor angular velocities. The new simplified nonlinear system, denoted (SNLS), is
in the first equation and takes into account the counter-electromotive torque in the arm and rotor angular velocities. The new simplified nonlinear system, denoted (SNLS), is
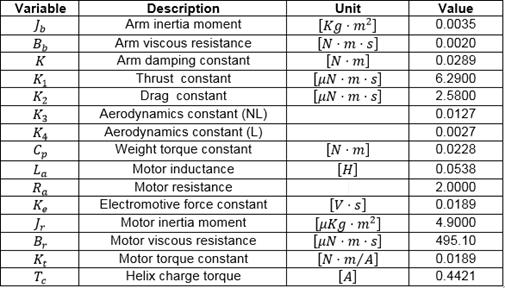
The variables and parameters are described in Tables 1 and Table 2 which were identified by using the methodology proposed in (Apkarian et al., 2011). Since the actual measurements of the system are for the variables 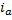 and
and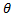 , then our analysis is based on these two variables.
, then our analysis is based on these two variables.
The estimation of the fractional orders of derivatives of the model is made by an extended Kalman Filter (EKF) procedure for which we follow (Sierociuk and Dzieliski, 2006); here a fractional order parameter estimation is proposed by the authors, this methodology is based on the Grünwald-Letnikov definition and uses an EKF structure which is described below.
2.2 EKF structure estimation
Consider the following discrete nonlinear system:
where:
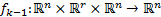 is a discrete vector field that relates the system state variables at instant
is a discrete vector field that relates the system state variables at instant 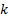 , with themselves and the uncertainty of modeling at instant
, with themselves and the uncertainty of modeling at instant 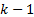 .
.
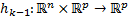 is a discrete vector field that relates the system state variables with the output variables.
is a discrete vector field that relates the system state variables with the output variables.
 and
and 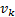 represent modeling uncertainty and measurement noise respectively.
represent modeling uncertainty and measurement noise respectively.
 and
and 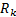 are the matrices of variance in modeling uncertainty and measurement noise respectively.
are the matrices of variance in modeling uncertainty and measurement noise respectively.
There are a prediction step and a correction step denoted by the indexes (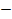 ) and (
) and (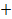 ) respectively. First the initial conditions for the EKF are determined by the following equations where
) respectively. First the initial conditions for the EKF are determined by the following equations where 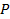 is the covariance matrix of the states.
is the covariance matrix of the states.
Let 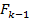 be the Jacobian matrix of
be the Jacobian matrix of 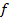 at time step
at time step 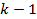 . Thus, the prediction step is given by
. Thus, the prediction step is given by
Finally, the correction step or state estimation is given by
where 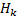 is the Jacobian matrix of
is the Jacobian matrix of  at time step
at time step 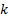 .
.
It should be noted that the state estimation requires system measurements and an idea of the noise variance present in these measurements and in the model.
3. Results and discussion
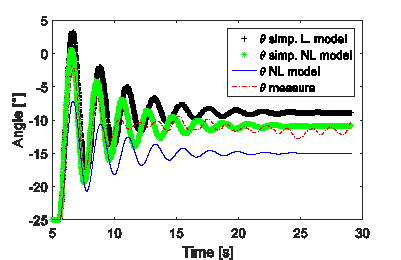
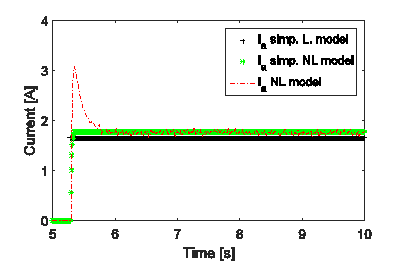
In Figures 2andFigure 3, a time step response of the three models are shown, this simulation was done by applying Euler method with step size 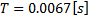 , and an input voltage
, and an input voltage 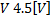 , which are the same step size and voltage of the actual measurements, which are also shown in the figures. The best agreement with experimental results is obtained by the simplified nonlinear model (SNLS) and Table 3 is a short summary of this fact.
, which are the same step size and voltage of the actual measurements, which are also shown in the figures. The best agreement with experimental results is obtained by the simplified nonlinear model (SNLS) and Table 3 is a short summary of this fact.
3.1 Fractional model for the system
A fractional version of the simplified nonlinear model is denoted (FSNLS) and is given by
To evaluate the performance of the new model a thorough sensitivity analysis is implemented. The unknown parameters are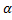 ,
,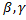 and
and 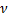 in
in 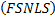 which are allowed to take values in
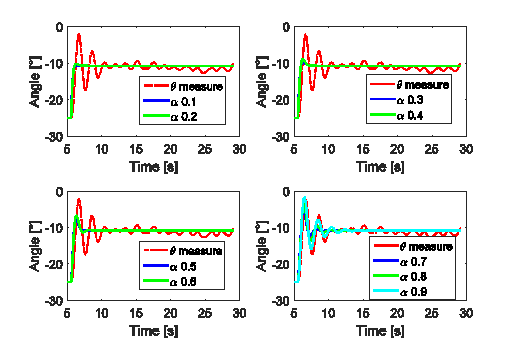
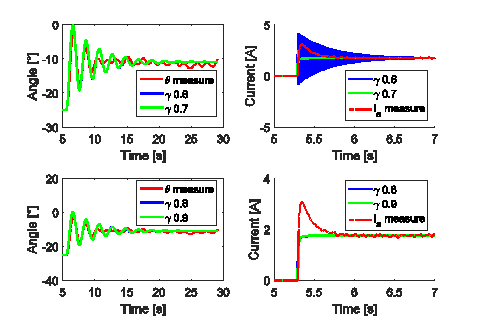
which are allowed to take values in 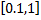 . One of the main observations is that if the first and third equations in (FSNLS) had fractional derivatives, the matching with measurements is optimal. Figures 4 and Figure 5 illustrate this fact.
. One of the main observations is that if the first and third equations in (FSNLS) had fractional derivatives, the matching with measurements is optimal. Figures 4 and Figure 5 illustrate this fact.
Based on a sensitivity analysis reported in (Rendón, 2018), the fractional model is given by (FSNLS) with 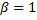 and
and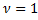 . That is, the second and fourth equations are not fractional. The selection of the fractional derivative orders
. That is, the second and fourth equations are not fractional. The selection of the fractional derivative orders 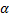 and
and 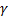 is made by an extended Kalman filter procedure described below.
is made by an extended Kalman filter procedure described below.
3.2 Parameter Estimation
In (Sierociuk and Dzieliski, 2006) it is shown that the EKF structure is strongly coupled to the fractional order parameters of the GL definition. The additional terms in the definition are considered as modeling noise and the covariance matrix 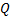 is modified by a neural network. We take a different strategy given below. It consists on a discrete redefinition of model (FSNLS) changing GL derivate definition to Caputo derivative definition and parameters
is modified by a neural network. We take a different strategy given below. It consists on a discrete redefinition of model (FSNLS) changing GL derivate definition to Caputo derivative definition and parameters 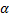 and
and 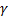 are included as unknown parameters of the system.
are included as unknown parameters of the system.
If we also have the following measured variables and matrix variances of measurement and modeling
then it is possible to estimate the fractional parameters 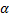 and
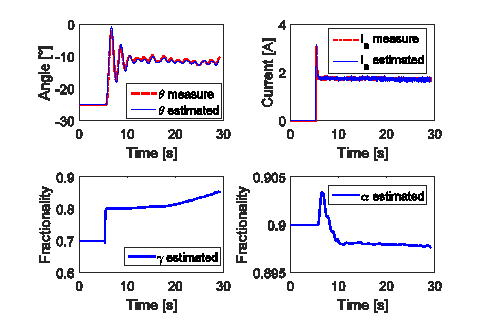
and 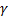 based on EKF methodology. Figure 6 illustrates this point. No attempt on the identification of fractional orders
based on EKF methodology. Figure 6 illustrates this point. No attempt on the identification of fractional orders 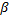 and
and 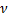 was made due to the results of the sensitivity analysis. Notice that the choices of
was made due to the results of the sensitivity analysis. Notice that the choices of 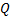 and
and  are based on the scaling of the measurements and some knowledge on the measurements and model noise variation.
are based on the scaling of the measurements and some knowledge on the measurements and model noise variation.
Figure 6 exhibits stationary behavior for parameter 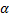 and a less stationary trajectory for
and a less stationary trajectory for 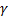 . Several fractional orders can be selected according to our results. Our pick is
. Several fractional orders can be selected according to our results. Our pick is 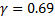 and
and 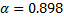 wich are among the best considered.
wich are among the best considered.
Table 4 and Figure 7 summarize the results. They indicate that the fractional model with GL derivative is an improvement over the classical model for this electromechanical device. We believe our claim can be verified by other researchers. Notice that the fractional model detects the initial current overshoot and none of the classical models introduced above are able to do that.
4. Conclusions
In this paper a new methodology for fractional modeling of a dynamical electromechanical nonlinear system is proposed. As a result, it turns out that fractional order derivatives in two of the four equations of system (FSNLS) provide an improvement over classical models. We reach this conclusion by considering actual measurements and a fractional parameter estimation based on an extended Kalman Filter (EKF) process.