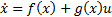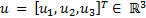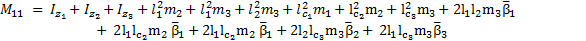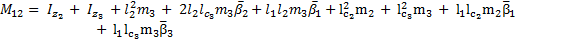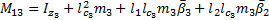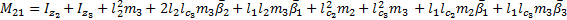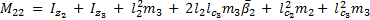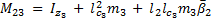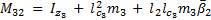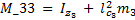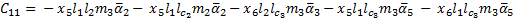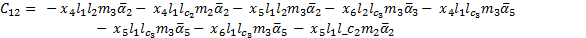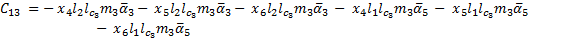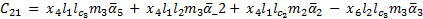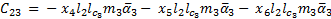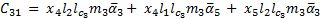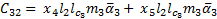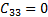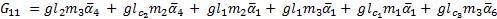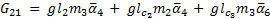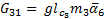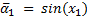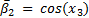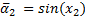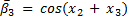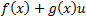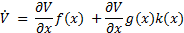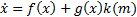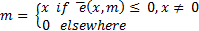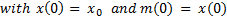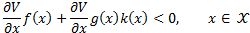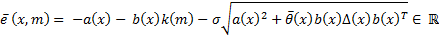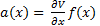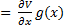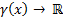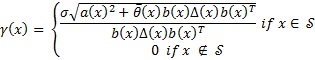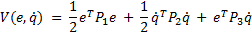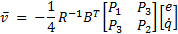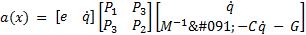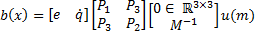1. Introduction
In recent years, technological advances in computer systems and sensors has lead in the development and application of advanced control theories and robotics. These advances are presented jointly, since the nonlinear models of robots have served as a good study case in order to illustrate the general concepts of analysis and design of advanced control theories (Canudas de Wit, Siciliano, & Bastin, 1996), for example: adaptive control (Tso & Lin, 1996), sliding modes control (Zhao, Sheng, & Liu, 2014), Lyapunov based control (Halalchi, Bara, & Laroche, 2010), nonlinear predictive control (Wilson, Charest, & Dubay, 2016), fuzzy logic control (Chen, Wang, Zhai, & Gao, 2017), among others. The main reason lies in its ability to manipulate materials, parts, tools or specialized devices by programming their movements.
It is well known that implementation of control theories in digital systems is possible by two kinds of control models: TTC and ETC. The first model consists of the measurement of system parameters uniformly in time with a sampling period 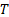 , and likewise has to update the signal control periodically for every time instant
, and likewise has to update the signal control periodically for every time instant 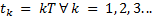 (Durand, and Guerrero-Castellanos, Marchand, & Guerrero-Sánchez, 2013). Furthermore, this model can be separated in two ways: continuous control by emulation and digital control. The continuous control by emulation is possible, if and only if, an enough small sampling time is guaranteed to ensure acceptable system performance. However, this constraint cannot always be guaranteed for all systems, due to the sampling devices and computer systems may present delays and errors of digitalization. On the other hand, the digital control is a mature and well known field for linear systems. However, when this is applied to nonlinear systems it may cause instability in the system because the digital control is based on transforming the continuous time system to discrete time, and afterwards to design a control law in discrete time. This process requires obtaining analytical nonlinear models in exact discrete time which implies solving a nonlinear explicit initial value problem (Monaco & Normand-Cyrot, 2007). The second approach is based on the execution of the control strategy by activating the event function. The activation of the event function occurs when a system performance constraint is violated.
(Durand, and Guerrero-Castellanos, Marchand, & Guerrero-Sánchez, 2013). Furthermore, this model can be separated in two ways: continuous control by emulation and digital control. The continuous control by emulation is possible, if and only if, an enough small sampling time is guaranteed to ensure acceptable system performance. However, this constraint cannot always be guaranteed for all systems, due to the sampling devices and computer systems may present delays and errors of digitalization. On the other hand, the digital control is a mature and well known field for linear systems. However, when this is applied to nonlinear systems it may cause instability in the system because the digital control is based on transforming the continuous time system to discrete time, and afterwards to design a control law in discrete time. This process requires obtaining analytical nonlinear models in exact discrete time which implies solving a nonlinear explicit initial value problem (Monaco & Normand-Cyrot, 2007). The second approach is based on the execution of the control strategy by activating the event function. The activation of the event function occurs when a system performance constraint is violated.
The ETC offers stability and a decrease in the number of control signal updates. As a result, the computational load decreases as at the same time as the energy consumption. Consequently, the ETC have been applied in some works: in (Villarreal-Cervantes, Guerrero-Castellanos, Ramírez-Martínez, & Sánchez-Santana, 2015) a comparison between an ETC and a Calculated Torque Control (CTC) are presented for the (3.0) mobile robot. The experimental results indicate a decrease of 23.73% in the number of updates of the ETC signal is obtained, compared to that required by the CTC. In (Tripathy, Kar, & Paul, 2014) the design of an ETC strategy based on robust control is proposed. This is validated by simulation in a SCARA type robot with two degrees of freedom, where the results showed asymptotic convergence with or without the presence of some disturbance. In (Durand, and Guerrero-Castellanos, Marchand, & Guerrero-Sánchez, 2013) the stabilization of an inverted pendulum by means of an ETC strategy is presented where the activation mechanism, based on the Lyapunov stability approach, is obtained through the methodology in (Marchand, Durand, & Guerrero Castellanos, 2013). Experiments and analysis of results in real time showed an approximate reduction between 98% and 50%; this compared to the classic scheme presented in the TTC.
Despite the benefits provided by the ETC, few results have been reported in the framework of robotics and mechatronics such as those mentioned above. For this reason, in the present work an ETC for the regulation of a robot manipulator with three DoF, which includes gravitational terms, is proposed. The strategy of ETC is based on the dynamic model of the manipulator robot; for this reason, in Section 2 the model is presented in state space. Likewise, the mathematical preliminaries concerning the stabilization of nonlinear systems under the Event-Triggered approach are given. In Section 3, the existence of a Lyapunov Control Function is shown as well as its mathematical proof. In addition, the event function that triggers the ETC strategy based on a CTC for the manipulator robot is developed. Comparative results of the ETC with a CTC is performed in Section 4. Finally, the conclusions of the present work are drawn in Section 5.
2. Mathematical Preliminaries
In the next Section, the dynamic model of the manipulator robot with three degrees of freedom is shown. Likewise, some relevant aspects on stabilization of nonlinear systems through the ETC are illustrated. These preliminaries will be necessary for the further development of the ETC, which will be used to stabilize the system at some desired point.
According to Kelly and Loria (Kelly, Santibáñez, & Loría, 2005), a manipulator robot is an articulated mechanical arm composed of links interconnected through joints, which allow a relative movement between two consecutive links.
Manipulator robot dynamic model
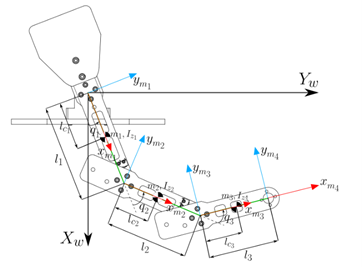
Figure 1 shows the schematic diagram of the manipulator robot, which consists of three revolute joints. The dynamic and kinematic parameters of the 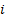 -th link are given by the distance between the axis of rotation to the center of mass
-th link are given by the distance between the axis of rotation to the center of mass  , the inertia
, the inertia  , the mass
, the mass  , and the link length
, and the link length 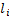 , with
, with 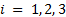 .
.
Let Equation 1 the representation in state variables of the dynamic model of the manipulator robot, where 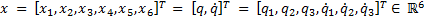 is the state vector corresponding to the angular position
is the state vector corresponding to the angular position 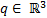 and velocity
and velocity 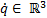 vectors, expressed in the joint space for each degree of freedom.
vectors, expressed in the joint space for each degree of freedom.
where:
The elements of the inertial matrix 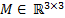 are:
are:
The elements of the Coriolis and Centrifugal matrix 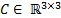 are represented by:
are represented by:
General formula of Event-Triggered Control
The ETC approach is restricted to the study of dynamic systems that have the form shown in Equation 2, where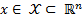 ,
, 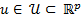 ,
, 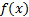 and
and 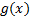 are smooth Lipschitz functions that vanish at the origin.
are smooth Lipschitz functions that vanish at the origin.
In the present work the stabilization case at the origin has been considered. If the system supports a state feedback 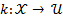 which stabilizes the system asymptotically, then there exists a LCF
which stabilizes the system asymptotically, then there exists a LCF 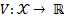 , which is a smooth and positive defined function, resulting in Equation 3.
, which is a smooth and positive defined function, resulting in Equation 3.
The ETC approach in general requires two functions
Event function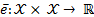 indicating whether it is necessary to update (
indicating whether it is necessary to update ( ) or not (
) or not ( ) the control signal. The event function
) the control signal. The event function 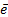 uses the current state vector
uses the current state vector 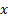 as input, and a memory parameter
as input, and a memory parameter 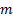 from the vector
from the vector 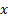 corresponding to the last instant of time in which an event function
corresponding to the last instant of time in which an event function 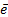 became negative.
became negative.
Feedback function: A state feedback is when 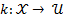 . This function is calculated, if and only if, the event function is activated.
. This function is calculated, if and only if, the event function is activated.
Definition1. (Marchand, Durand, & Guerrero Castellanos, 2013): An ETC (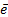 ,
,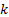 ) is said to be semi-uniformly MSI (Minimal Sampling Interval property) if for all
) is said to be semi-uniformly MSI (Minimal Sampling Interval property) if for all 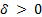 and all
and all 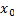 on the radio sphere
on the radio sphere  with center at the origin
with center at the origin 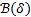 , the time interval between two consecutive events can be bounded below by some
, the time interval between two consecutive events can be bounded below by some 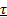
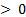 .
.
It is well known that for nonlinear systems of the form (2) with a ETC (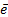 ,
,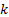 ) semi-uniform MSI, the solution for Equation 2, with initial conditions
) semi-uniform MSI, the solution for Equation 2, with initial conditions 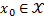 at the instant
at the instant 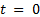 , is defined for all
, is defined for all 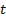 positive as the solution to the differential system in Equations 4 and 5.
positive as the solution to the differential system in Equations 4 and 5.
Theorem 1. (Universal Event-Triggered formula (Marchand, Durand, & Guerrero Castellanos, 2013)): If there exists a LFC for the system (2), then the event-based feedback (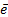 ,
,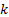 ) defined above is semi-uniform MSI smooth in
) defined above is semi-uniform MSI smooth in 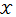 such that we have Equation 6.
such that we have Equation 6.
where 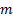 is defined in Equation 5 and, the feedback control
is defined in Equation 5 and, the feedback control 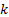 and the event function
and the event function 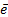 is given by Equations 7 and 8 respectively.
is given by Equations 7 and 8 respectively.
with:
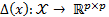 wich that
wich that 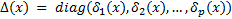 is a smooth and definite positive function in
is a smooth and definite positive function in 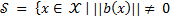
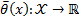 is a smooth function, such that
is a smooth function, such that  vanishes at the origin and ensures the inequality
vanishes at the origin and ensures the inequality 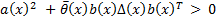 in
in 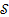 .
.
 is an adjustable control parameter in
is an adjustable control parameter in 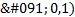 .
.
3. Design Control Strategy
In this section the design of the ETC strategy for the stabilization of the manipulator robot is described.
Lyapunov Control Function
Considering the regulation problem and a variable change  , the Lyapunov Function
, the Lyapunov Function  defined in Equation 10 is proposed, where
defined in Equation 10 is proposed, where 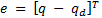 is the error between the desired angular position
is the error between the desired angular position 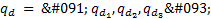 and the real one and
and the real one and  are symmetric and positive defined matrices.
are symmetric and positive defined matrices.
Considering the control system in Equation 11, then 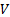 is a LCF for the system shown in Equation 1 relative to the equilibrium point
is a LCF for the system shown in Equation 1 relative to the equilibrium point 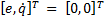 .
.
with:
where 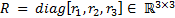 is a positive definite gains matrix and
is a positive definite gains matrix and 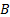 is given by
is given by  .
.
As a result of applying the control strategy shown in Equation 11 to the dynamic system in Equation 1, the system is asymptotically stable, so that 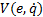 is a LCF for that system. It is worth mentioning that, in the present work requires the control strategy shown in Equation 11 in order to obtain a closed-loop linear system and hence the feedback control in Equation 7 is not used anymore and only the event function of the ETC depends on the LCF.
is a LCF for that system. It is worth mentioning that, in the present work requires the control strategy shown in Equation 11 in order to obtain a closed-loop linear system and hence the feedback control in Equation 7 is not used anymore and only the event function of the ETC depends on the LCF.
The proof is given in Appendix A.
Event function for the manipulator robot
Once the LCF is established, it is possible to develop the ETC methodology proposed in (Marchand, Durand, & Guerrero Castellanos, 2013). In order to obtain the functions 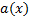 and
and 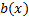 , necessary for the event function in Equation 8; the temporal derivative of the LCF in Equation 10 is taken again evaluated along the trajectory in Equation 1, as seen in Equation 12.
, necessary for the event function in Equation 8; the temporal derivative of the LCF in Equation 10 is taken again evaluated along the trajectory in Equation 1, as seen in Equation 12.
Therefore, the functions a(x) and b(x) are given by Equations 13 and 14.
4. Results
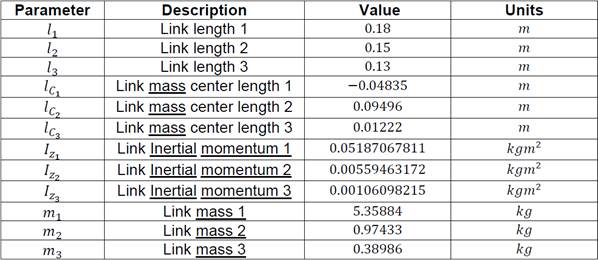
In the current section, the operation of the ETC strategy applied to a three DoF manipulator robot is analyzed, considering the regulation problem in the joint space. For this purpose, a comparison is made between the effectiveness of the ETC and a Computed Torque Control for the stabilization of the manipulator robot. The manipulator robot parameters are shown in Table 1.
To carry out experiments in simulation, the rest position is considered as the initial condition for the manipulator robot, i.e., 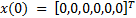 . In addition, four different desired angular positions have been taken into account:
. In addition, four different desired angular positions have been taken into account: 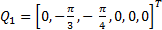 ,
,  ,
, 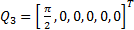 and
and 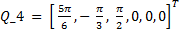 , such that the manipulator robot reaches them in sequential order. These positions must be reached in a maximum time of
, such that the manipulator robot reaches them in sequential order. These positions must be reached in a maximum time of 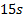 , therefore, the final simulation time will be
, therefore, the final simulation time will be 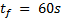 . The experiments were performed in Matlab, with a fixed sampling time of
. The experiments were performed in Matlab, with a fixed sampling time of 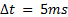 .
.
On the other hand, the proposed parameters for the ETC are the following: i) event frequency 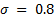 and ii) functions
and ii) functions 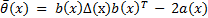 and
and 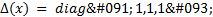 . As noted above, the gains
. As noted above, the gains 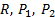 and
and 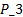 are parameters in common between the two control strategies ETC and CTC. Therefore, these parameters are shown below: i) matrix of gains
are parameters in common between the two control strategies ETC and CTC. Therefore, these parameters are shown below: i) matrix of gains  , obtained based on tests in simulation and ii) matrix of gains
, obtained based on tests in simulation and ii) matrix of gains 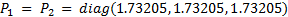 and
and 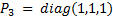 , obtained from the “care” function of Matlab, which calculates the solution of the Riccati Algebraic equation in continuous time. Those gains are used in both control strategies in order to make a fair comparison.
, obtained from the “care” function of Matlab, which calculates the solution of the Riccati Algebraic equation in continuous time. Those gains are used in both control strategies in order to make a fair comparison.
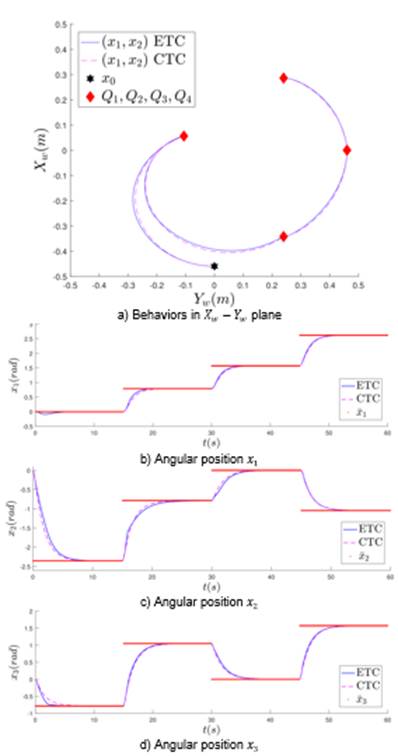
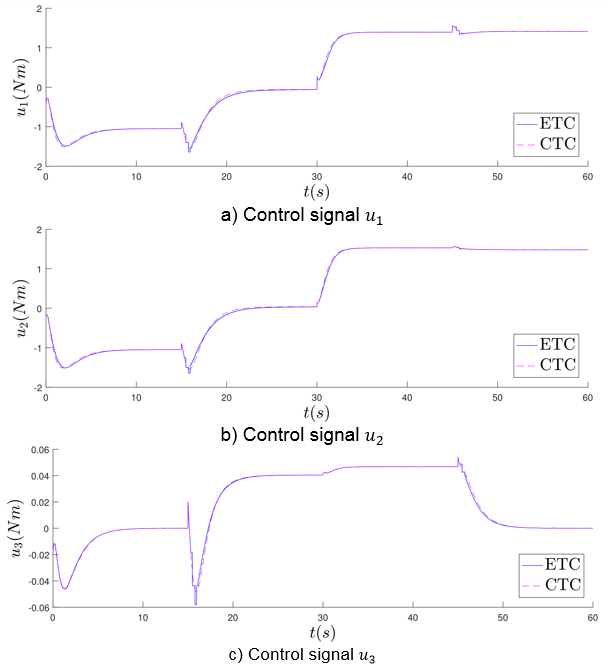
Figure 2a represents the behavior of the end effector of the manipulator robot in the workspace 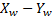 and in Figures 2b-2d displays the angular position of each link for both control strategies. Similar behavior in both control strategies is observed. In order to provide a quantitative results three performance indices are considered in Table 2. Those indices are Integral Absolute Error (AIE), the Integral Time-weighted Absolute Error (ITAE) and the Integral Square Error (ISE). It is clear that the CTC presents a better performance than the ETC in the specified task. In addition, it is possible to deduce that the error converges to zero in both control approaches. These results indicate that the ETC system does not significantly impair closed loop performance.
and in Figures 2b-2d displays the angular position of each link for both control strategies. Similar behavior in both control strategies is observed. In order to provide a quantitative results three performance indices are considered in Table 2. Those indices are Integral Absolute Error (AIE), the Integral Time-weighted Absolute Error (ITAE) and the Integral Square Error (ISE). It is clear that the CTC presents a better performance than the ETC in the specified task. In addition, it is possible to deduce that the error converges to zero in both control approaches. These results indicate that the ETC system does not significantly impair closed loop performance.
In relation to the respective control signals for both control strategies, in Figure 3 their behavior are shown. To evaluate the energy consumption performance of both strategies, in the last row of Table 2 the total torque required to control the manipulator robot is given, which results that the ETC consumes a lower energy than the CTC.
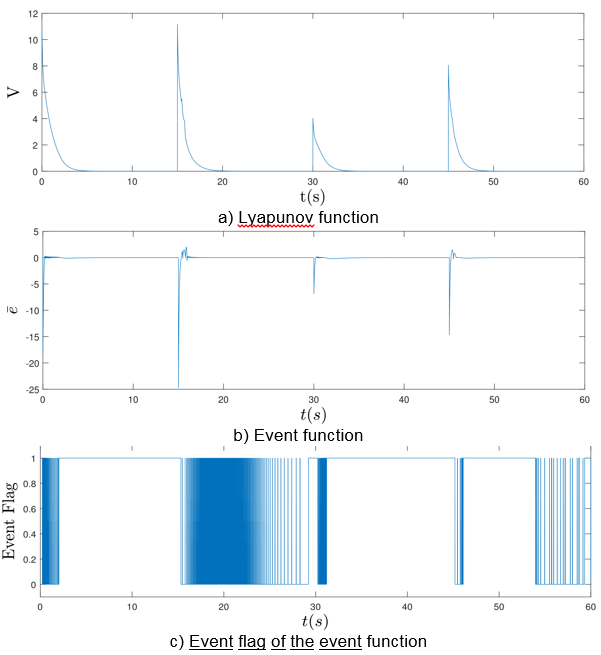
Finally, in the Figure 4a the Lyapunov function is shown, where the function grows when a change between positions is required, and the convergence around zero occurs when the system stabilizes at the desired position; similarly, this behavior is presented in the event function shown in Figure 4b. Furthermore, Figure 4c shows the event flag, where “1” (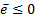 ) indicates the update of the control signal and “0” (
) indicates the update of the control signal and “0” ( ) means that the previous control signal is used.
) means that the previous control signal is used.
Taking the sampling time of 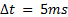 , the classical approach of CTC based on TTC requires a total of
, the classical approach of CTC based on TTC requires a total of 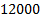 control signal updates, meanwhile the ETC updates
control signal updates, meanwhile the ETC updates 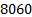 times the control signal. Therefore, the ETC decreases by
times the control signal. Therefore, the ETC decreases by 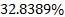 the number of required updates compared to the CTC. Consequently, computational calculation and energy consumption is also reduced
the number of required updates compared to the CTC. Consequently, computational calculation and energy consumption is also reduced
5. Conclusions
In the present work a control strategy triggered by events was presented, which was applied in simulation to a robot manipulator of three degrees of freedom. To evaluate the performance of the ETC compared to a CTC, three performance indices were computed. These results showed that the CTC gives a better behavior than the ETC, because the ETC does not require the continuous update of the control signal to perform the regulation task. Therefore, the error in the ETC is larger. On the other hand, based on the tests performed, it was found that the ETC showed an acceptable performance with asymptotic convergence, obtaining some benefits without significantly affecting the performance of the system.
Furthermore, control signal updates required by ETC is reduced by 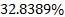 compared with CTC based on the classical method of TTC. Due to computational calculation is reduced, consequently the energy consumption is lower. On the other hand, due to control signal is updated aperiodically, it is possible to process other task in the time when the control signal is not updated.
compared with CTC based on the classical method of TTC. Due to computational calculation is reduced, consequently the energy consumption is lower. On the other hand, due to control signal is updated aperiodically, it is possible to process other task in the time when the control signal is not updated.