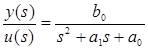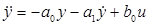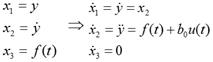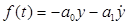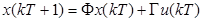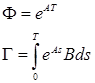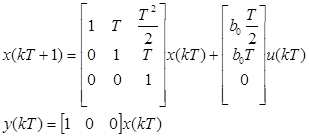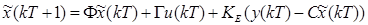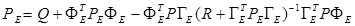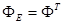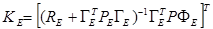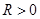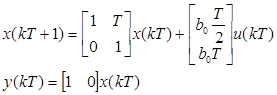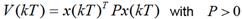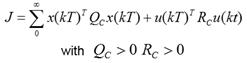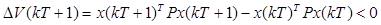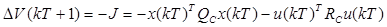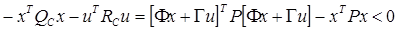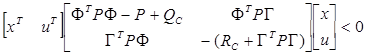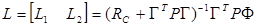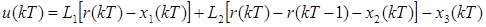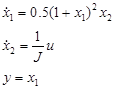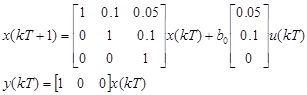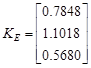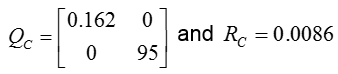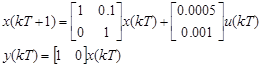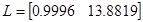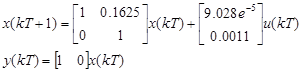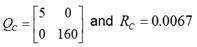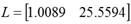1. Introduction
One of the main concerns in control systems is to find a suitable model for control design, from classical to modern control theory, finding a model that could represent the increasing complexity and nonlinearities of systems is a difficult step to be fulfilled in order to find a stabilizing controller for a given systems, this need leads to a shift on the control paradigm, (Gao 2006).
The main idea behind Active Disturbance rejection control or ADRC is to build a control law based on Active estimation and rejection of the generalized disturbance using an Extended State Observer or ESO to estimate the internal plant dynamic and external disturbances requiring little information of the plant, (Zheng 2009). This method has been tested in several applications, from process found on laboratories to complex aerospace systems as seen on: (Teppa et al 2012), (Zheng 2009), (Zheng et al 2010), (Alexander et al 2008) and (Tanaka et al 2015).
On this paper, the Extended State Observer is transformed into an Extended State Predictor; taking as starting point the works of (Miklosovic et al 2006) and (Tanaka et al 2015) a Kalman filter in prediction mode is built, this done to deal not only with the unknown dynamics and disturbances but also unknowns time delays. On the other hand, the controller is obtained by using the LMI approach as systematic way to tune the controller not only when the dynamic of the plant is unknown but also if the process is presented in polytopic form.
The paper is structured as follows; first the Extended State Predictor is presented followed by the controller design using the LMI approach to finally test on a benchmark process which in this case is the Cayley-Rodriguez representation of the Monoaxial satellite.
2. Methodology
2.1. Extended State Predictor
First, consider a nonlinear plant described by the differential Equation 1.
The design procedure of the Predictive ADRC controller proposed on this work is divided in two steps following (Gao 2006) ; the first step comprehend the design of an Extended State Predictor (ESP) using (Miklosovic et al 2006) as starting point, the second step involves the design of the corresponding controller using the parameters estimated by the ESP.
In order to build the corresponding ESP, consider the unknown second order transfer function in Equation 2.
this can be rewritten as in Equation 3.
Using the auxiliary representation presented on (Gao 2006) and (Teppa et al 2012) we have Equation 4.
This is written in the state space representation in Equation 5.
Equation 5 is discretized assuming a non-pathological sampling period T according to (Miklosovic et al 2006) using (Astrom et al 1998), as in Equation 6.
Where (Equation 7):
According to Equation 7, Equation 5 becomes Equation 8.
On this work is proposed to use Equation 8 with a Kalman Filter on prediction mode, for this reason, consider (Astrom et al 1998) where the system is presented as a one step ahead predictor of the form in Equation 9.
The value of K E is obtained by solving the Ricatti Equation, (Astrom et al 1998), (Tanaka et al 2015) as in Equation 10.
The gain of the predictor is described by Equation 11.
2.2. Controller Design
Once the Extended State Predictor is designed, the following step is to build the corresponding controller. Consider a reduced representation of Equation 8, which is controllable and observable as in Equation 12.
On this work b 0 is considered as part of the system to be controlled, on (Gao 2006) and (Teppa et al 2012) a pole placement design method is used as starting point, whereas this work proposes the use of an LMI in discrete time.
According to (Kaskurewicz et al 2006), (Xue et al 2009), (Teppa 2012), (Oishi 2008), (Hermann 2006) and (Alamo 2012) consider the Lyapunov equation on discrete time (Equation 13).
Find a desirable control law that minimizes the following cost function (Equation 14).
First, the difference operator is applied on Equation 13; this is shown in Equation 15.
Where 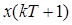 is represented by Equation 12 and we have Equation 16.
is represented by Equation 12 and we have Equation 16.
Substituting Equation 12 and Equation 16 into Equation 15, the Equation 17 is obtained.
Rewriting Equation 17 it is possible to find the control law that stabilizes the system on Equation 12, by solving the Linear Matrix Inequality in Equation 18, with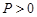 , (Stoorvorgel et al 1998).
, (Stoorvorgel et al 1998).
Where the control law is expressed in Equation 19.
From the values of Equation 19, the parameters of the ADRC controller are obtained according to (Zheng 2009) adapted for discrete time on this work from (Jantzen 1998), this leads to Equation 20.
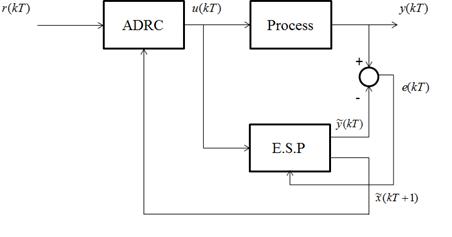
The Predictive ADRC controller is represented in Figure 1.
3. Case Study
In order to study the Predictive ADRC controller presented before, the Cayley-Rodriguez representation of the Monoaxial satellite found in (Sira et al 2005) and (Andymar 2006) is selected, this is a nonlinear plant with unstable linear models in any equilibrium point, and is represented by Equation 21.
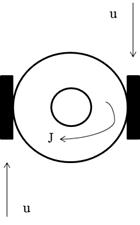
Where 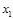 is the orientation angle of the satellite respect of an oblique’s axis and
is the orientation angle of the satellite respect of an oblique’s axis and 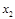 is the angular speed respect the principal axis, J is the inertia and
is the angular speed respect the principal axis, J is the inertia and  is the applied torque, as seen in Figure 2 (Sira et al 2005).
is the applied torque, as seen in Figure 2 (Sira et al 2005).
The first step is to build the discrete time representation of the unknown system, assuming a sampling period of T=0.1 seg and considering b 0 =0.01 substituting on Equation 8; the unknown model is shown in Equation 22.
Using Equation 22, the gain of the predictor K E is shown in Equation 23.
Once build the ESP, the next step is to build the controller, by choosing Equation 24.
And the reduced Equation 12 can be seen in Equation 25.
With all this on mind and solving for Equation 18 the control law that minimizes Equation 14, we have Equation 26.
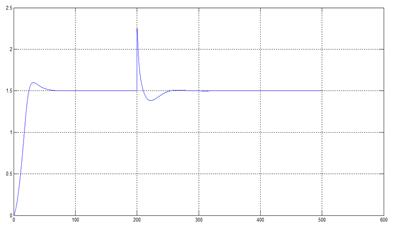
The Matlab/Simulink toolboxes where used for all the calculations. On (Sira et al 2005) the Output of the system is x 1 and its desired reference is x 1 =1.5 with J=90 (Andymar 2006), the simulation is presented in Figure 3 against a disturbance of the 50% of the nominal value.
As shown on Figure 3, the Predictive ADRC effectively regulates the system and also has the capability to reject larger disturbances.
On the second experiment, the discrete nominal linearized model of Equation 22 is used, assuming x 1 =1.5 and x 2 =0 as equilibrium points, the discrete linearized model with sampling period T=0.1seg is presented in Equation 27.
The ESP presented before on Equation 22 and Equation 23 is used, so this experiment is limited to the control law calculation, on this case assuming Equation 28.
The controller is shown in Equation 29.
Against the same reference signal and disturbance, the system is shown in Figure 4.
The response is improved when the overshoot is reduced; this is because the controller has more information of the system than the unknown model presented before.
On both cases including b 0 =0.01 into the control calculation and eliminating from the block diagram as presented on Equation 20 and Figure 1; leads to a reduction on the sensibility on the control loop, mostly against measurable and not measurable disturbances.
4. Conclusions
On this paper a modification of the typical ADRC algorithm is presented, first an ESO is used as a predictive estimator that feeds the ADRC controller on discrete time, which is tuned using the LMI´s approach, resulting on a controller who can reject disturbance and track the desired reference, on future works a physical implementation of this controller is considered on test system.