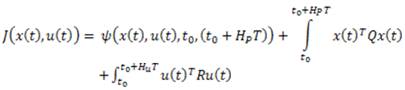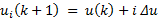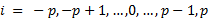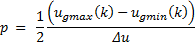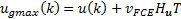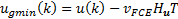1. Introduction
Model predictive control (MPC) is a successful control technique for plants with slow dynamics like chemical and petrochemical processes. Although these kind of plants are nonlinear, in some cases, the performance of linear MPC has been suitable (Darby & Nikolaou, 2012; Mayne, 2000; Rao & Rawlings, 2000; Xi, Li, & Lin, 2013). However, in order to improve the MPC performance a nonlinear model of the process should be used, which leads to nonlinear MPC (NMPC) (Chen & Allgöwer, 1998; De Oliveira, 1996). The main disadvantage of NMPC is the complexity related with the resulting nonlinear optimization problem, which is usually nonconvex (Mishra, 2011) and must be solved in real time (Camacho & Bordons, 2007; Chen & Allgöwer, 1998). A typical solution to solve the resulting nonlinear program (NLP) in real time implies the use of high performance computing, however, in industrial facilities it is not available (Richalet, 1993). Additionally, any required complex computation for control implies an increase in maintenance protocols for which the fail probabilities also increase.
Available numerical methods to solve the non-convex optimization problems for NMPC can be classified in three sub-groups:  Direct enumeration, which is not very efficient at the computation level when the process model is not compact enough, but with models that can be evaluated at a good speed, this technique always produces feasible solutions and quite close to the global optimum;
Direct enumeration, which is not very efficient at the computation level when the process model is not compact enough, but with models that can be evaluated at a good speed, this technique always produces feasible solutions and quite close to the global optimum;  dynamic programming, like iterative dynamic programming (Luus, 1996) and blurred dynamic programming (Alkan, Erkmen, & Erkmen, 1994), but the disadvantage of dynamic programming methods is the high computation costs; and
dynamic programming, like iterative dynamic programming (Luus, 1996) and blurred dynamic programming (Alkan, Erkmen, & Erkmen, 1994), but the disadvantage of dynamic programming methods is the high computation costs; and 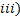 heuristic methods such as genetic algorithms, Bacterial Chemotaxis (BCh) and simulated annealing. Although those methods provide feasible solutions very close to the global optimum, they consume a lot of computation time (Holland, 1992). Therefore, to provide simple optimization procedures allows the industrial implementation of NMPC. The aim of this work is to propose the restricted enumeration method to solve the nonlinear-nonconvex optimization problem of NMPC to increase the possibilities of its implementation in industrial processes.
heuristic methods such as genetic algorithms, Bacterial Chemotaxis (BCh) and simulated annealing. Although those methods provide feasible solutions very close to the global optimum, they consume a lot of computation time (Holland, 1992). Therefore, to provide simple optimization procedures allows the industrial implementation of NMPC. The aim of this work is to propose the restricted enumeration method to solve the nonlinear-nonconvex optimization problem of NMPC to increase the possibilities of its implementation in industrial processes.
This article is structured as follows. In Section 2, the problem formulation is stated. In Section 3, the optimization by restricted enumeration is proposed. Subsequently, in Section 4 an illustrative case study is presented, showing the suitability of this proposal. Finally, conclusions are given in Section 5.
2. Model predictive control
Model predictive control (MPC) is a control technique applicable to both linear and nonlinear systems, which is based on optimal control theory (Camacho & Bordons, 2007). MPC has its roots in the development of optimal control theory in the fifties of the twentieth century, but achieved its consolidation as an independent technique at the end of the seventies. In this kind of control, a process model predicts the evolution of the variables over a specified finite prediction horizon. Thus, an optimal control strategy is obtained by minimizing an objective function, which usually includes, among others, a term related to the error and another that penalizes the applied control effort, all on a finite prediction horizon. The control action is optimized over a control horizon, which is shorter or at most the same as the prediction horizon. Only the first calculated control action is applied to the process and the optimization is repeated at the next sampling time. Several works have shown that MPC allows the construction of stable control laws (Camacho & Bordons, 2007; Chen & Allgöwer, 1998; De Oliveira, 1996; Xi et al., 2013).
For linear system and quadratic objective function, MPC strategies are considered as well-founded subject in which stability, optimality and feasibility of control actions are guaranteed (Camacho & Bordons, 2007). In contrast, non-linear MPC arises when the prediction model is nonlinear and/or restrictions on the states of the process are included into the optimization problem. In this case, a nonlinear optimization problem must be efficiently solved to obtain the control actions. Those control actions should fulfill certain characteristics, including their feasibility. For nonlinear systems, the nonlinear MPC can be formulated as shown in Equations 1a - 1e.
Where  , Equation (1a), is the control performance objective function,
, Equation (1a), is the control performance objective function, 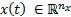 denotes the vector of state variables and
denotes the vector of state variables and 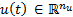 is the vector of manipulated inputs or calculated control actions. Process model is represented by Equation (1b) with corresponding initial conditions
is the vector of manipulated inputs or calculated control actions. Process model is represented by Equation (1b) with corresponding initial conditions 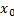 , Equation (1c), while Equation (1d)-(1e) are equality and inequality constraints for the process, respectively. The vector fields
, Equation (1c), while Equation (1d)-(1e) are equality and inequality constraints for the process, respectively. The vector fields  ,
, 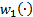 , and
, and 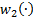 map from some open subsets
map from some open subsets 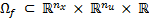 and
and  into
into 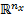 ,
, 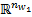 , and
, and 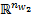 , respectively, and are assumed to be continuous in
, respectively, and are assumed to be continuous in 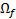 and
and 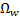 , respectively.
, respectively. 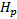 is the prediction horizon and
is the prediction horizon and 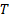 the sampling period.
the sampling period.
In general,  is expressed as shown in Equation 2.
is expressed as shown in Equation 2.
Where 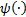 is a penalty function based on initial and terminal conditions of the system and integral terms evaluate the state transient behavior of the system for
is a penalty function based on initial and terminal conditions of the system and integral terms evaluate the state transient behavior of the system for 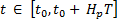 and the control action behavior for
and the control action behavior for 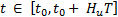 with
with 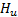 the control horizon.
the control horizon. 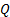 and
and  are positive definite matrices acting as weights for representing the biased solution between minimum error in process output but reduced control effort.
are positive definite matrices acting as weights for representing the biased solution between minimum error in process output but reduced control effort.
The basic MPC structure used in this paper is shown in Figure 1, where it is assumed that the complete state vector is available from direct measurements at the plant. This assumption was considered to avoid the implementation of a state estimator and to make easier the validation of the proposed optimization methodology. However, the use of this proposal with one or more estimators for those non-measured states is direct.
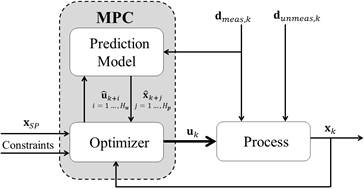
Fig. 1: Model predictive control structure. The state vector of the plant is assumed completely available.
As shown in Figure 1, the prediction model uses both input (manipulated and disturbances) and output information (states as measured variables) to compute the future estimated states  for a future horizon
for a future horizon 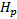 . At sampling time
. At sampling time 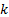 , the MPC given by Equation (1), predicts the set of control actions
, the MPC given by Equation (1), predicts the set of control actions 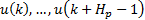 , which allow that the states track a predefined trajectory over the prediction horizon
, which allow that the states track a predefined trajectory over the prediction horizon 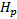 . This is possible with the manipulated variable executing the computed movements in the control horizon
. This is possible with the manipulated variable executing the computed movements in the control horizon 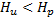 and guaranteeing feasibility respect to equality, Equation (1d), and inequality, Equation (1e), constraints. From time instant
and guaranteeing feasibility respect to equality, Equation (1d), and inequality, Equation (1e), constraints. From time instant 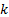 to time
to time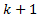 , only the first element of the computed sequence of manipulated variables is applied to the process. At
, only the first element of the computed sequence of manipulated variables is applied to the process. At  all the measurements are actualized allowing the prediction model to use
all the measurements are actualized allowing the prediction model to use 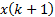 and
and  to compute the future state vector. The prediction horizon
to compute the future state vector. The prediction horizon 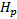 and control horizon
and control horizon 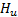 move a step forward, which is called moving horizon control.
move a step forward, which is called moving horizon control.
The solution of the optimization problem is the part of the NMPC algorithm with the highest computational cost, in particular when the considered model is non-linear and constraints are included. To this aim, in a general approach three kind of numerical methods can be used:  Direct enumeration,
Direct enumeration,  Dynamic programming methods (Alkan et al., 1994; Aydin, Bonvin, & Sundmacher, 2017; Binder, Cruse, Villar, & Marquardt, 2000; Holland, 1992), and
Dynamic programming methods (Alkan et al., 1994; Aydin, Bonvin, & Sundmacher, 2017; Binder, Cruse, Villar, & Marquardt, 2000; Holland, 1992), and 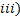 Heuristics methods. In this work, a direct enumeration method is proposed, which consists in the generation of possible control vectors to find a minimum value for the NMPC objective function. This control vectors are the position of the FCE during the prediction horizon Hp. It should be notice that the attained “degree of optimality” of the problem depends on the amount of control vectors that are generated. Under these circumstances, there are three different techniques to generate possible control vectors: Random, staggered and restricted enumeration. Random and staggered techniques chose the control vectors without knowledge of the process, while the restricted enumeration not only includes possible positions of actuator but also takes into account the dynamic response of the used final control element (FCE). The construction of this set of FCE movements imitates the branch and bound technique to solve decision trees used in Artificial Intelligence (AI). In this way, a drastic and organized reduction of the search space is obtained, and the time for solving the NMPC optimization problem is reduced compared to direct enumeration methods. Thus, the method of generating control vectors by restricted enumeration allows an organized and successful choice of the “near to best” control action at each sampling time unlike the other two previous methods (random and staggered). This technique is considered in this work and described in the following section.
Heuristics methods. In this work, a direct enumeration method is proposed, which consists in the generation of possible control vectors to find a minimum value for the NMPC objective function. This control vectors are the position of the FCE during the prediction horizon Hp. It should be notice that the attained “degree of optimality” of the problem depends on the amount of control vectors that are generated. Under these circumstances, there are three different techniques to generate possible control vectors: Random, staggered and restricted enumeration. Random and staggered techniques chose the control vectors without knowledge of the process, while the restricted enumeration not only includes possible positions of actuator but also takes into account the dynamic response of the used final control element (FCE). The construction of this set of FCE movements imitates the branch and bound technique to solve decision trees used in Artificial Intelligence (AI). In this way, a drastic and organized reduction of the search space is obtained, and the time for solving the NMPC optimization problem is reduced compared to direct enumeration methods. Thus, the method of generating control vectors by restricted enumeration allows an organized and successful choice of the “near to best” control action at each sampling time unlike the other two previous methods (random and staggered). This technique is considered in this work and described in the following section.
3. Optimization by restricted enumeration
Optimization by restricted enumeration (ORE) is a numerical method to solve nonlinear optimization problems. Some previous works report similar approaches to other tasks not related to MPC (Vatter, 2008) and (Zenem, Chehade, & Yalaoui, 2012). As it is known, the major obstacles to implement model predictive control (MPC) at industrial environments are two: the availability of a precise enough process model and the computational burden of optimization into MPC algorithm. The model availability is being solved with increasingly powerful modeling techniques. However, for reducing the optimization computational burden, it is necessary to try new approaches. In this sense, the ORE approach proposed here offers a set of possible solutions to the optimization problem. It should be highlighted that mentioned enumeration is non-exhaustive, i.e., only a part of all possible solutions are tested. The real movement capability of the final control element (FCE) is used as the criterion to perform the enumeration among all possible and feasible solutions. Compared to heuristic and gradient-based optimization methods, ORE is a technique with less computation effort and inherent convergence. Its application to MPC optimization solving was not found in the literature as a single topic. Additionally, ORE takes into account the characteristics of the FCE with a direct and simple industrial implementation. According to (Alvarez, 2000), ORE requires the following steps, which are modified in this paper for including the option of control horizon 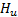 greater than
greater than 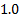 :
:
Create a grid step 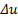 from the current position of the FCE acting over the manipulated variable, such that (Equations 3a - 3c):
from the current position of the FCE acting over the manipulated variable, such that (Equations 3a - 3c):
where 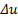 is selected as an enough fine and feasible FCE movement with detectable effect over process state. Note that coarse
is selected as an enough fine and feasible FCE movement with detectable effect over process state. Note that coarse 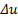 values will produce non-smooth state changes. Contrary, very fine
values will produce non-smooth state changes. Contrary, very fine 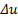 values will produce excessive computational burden and possibly the FCE will be unable to execute those fine movements. The
values will produce excessive computational burden and possibly the FCE will be unable to execute those fine movements. The 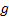 subindex indicates the grid current range of FCE incharged of execute the control action
subindex indicates the grid current range of FCE incharged of execute the control action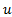 . This generates the new dynamic restriction
. This generates the new dynamic restriction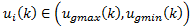 , with the limits calculated as:
, with the limits calculated as:
with 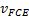 the operative speed of FCE in
the operative speed of FCE in 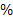 of movement per second,
of movement per second, 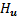 the number of movements considered for the FCE during optimization (called control horizon) and
the number of movements considered for the FCE during optimization (called control horizon) and 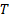 the time step of NMPC in seconds. The difference between
the time step of NMPC in seconds. The difference between 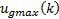 and
and 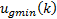 is called the restricted range of enumeration. This is the reason to call the current proposal as restricted enumeration, contrary to the known total enumeration.
is called the restricted range of enumeration. This is the reason to call the current proposal as restricted enumeration, contrary to the known total enumeration.
Eliminate from previous found grid all control actions out of feasible FCE range. In this way it is guaranteed that 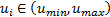 , with
, with 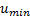 and
and  the extremes of real FCE, i.e., negative positions or FCE positions over
the extremes of real FCE, i.e., negative positions or FCE positions over  are not considered.
are not considered.
Test one to one each position of the final feasible stated grid around the current FCE position. Select as the best feasible control actions sequence (CAS) 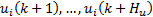 , which maxims the improvement of objective function for the MPC, Equation (1). The selected CAS is the solution to the optimization problem, which is feasible but not necessarily a local or global minimum.
, which maxims the improvement of objective function for the MPC, Equation (1). The selected CAS is the solution to the optimization problem, which is feasible but not necessarily a local or global minimum.
Note that the ORE method requires to tune only one parameter, namely 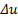 , because the other parameters:
, because the other parameters:  ,
, 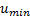 , and
, and 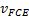 , are known from FCE coupling with the process and from FCE manufacturer manual.
, are known from FCE coupling with the process and from FCE manufacturer manual. 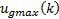 and
and 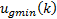 are time-dependent and must be calculated at each
are time-dependent and must be calculated at each 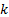 time, as it was shown. The option of one-step ORE and multi-step ORE is possible after modification proposed above regarding the original proposal. Next, these two options are exposed.
time, as it was shown. The option of one-step ORE and multi-step ORE is possible after modification proposed above regarding the original proposal. Next, these two options are exposed.
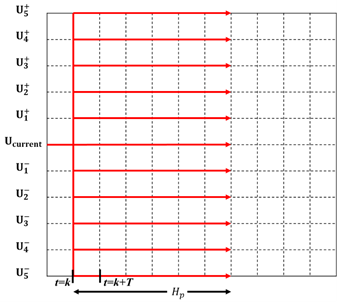
3.1 One-step ORE (H u =1)
The idea in this case is to select, from the set of generated and refined possible control action, the best one that minimizes the objective function of MPC (1) with 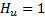 . The refined grid with the feasible FCE movements for current control actions is illustrated in Figure 2. Due to
. The refined grid with the feasible FCE movements for current control actions is illustrated in Figure 2. Due to 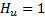 no subsequent movements of FCE are executed for
no subsequent movements of FCE are executed for 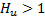 , i.e., after
, i.e., after  all FCE positions are equal to the selected
all FCE positions are equal to the selected 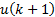 until reaching the
until reaching the 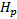 .
.
3.2 Multi-step ORE (H U >1)
Contrary to previous option, multi-step ORE changes the control action during two or more steps into the prediction horizon, in accordance with the control horizon value 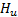 . Each FCE movement is calculated following the three-step procedure given above. In Figure 3 this option is illustrated for
. Each FCE movement is calculated following the three-step procedure given above. In Figure 3 this option is illustrated for 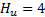 . In the same way that applied for one-step ORE, here after the fourth FCE movement the rest of FCE positions are keeped constant and equal to the last one
. In the same way that applied for one-step ORE, here after the fourth FCE movement the rest of FCE positions are keeped constant and equal to the last one 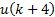 , until reach the end of the
, until reach the end of the 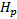 .
.
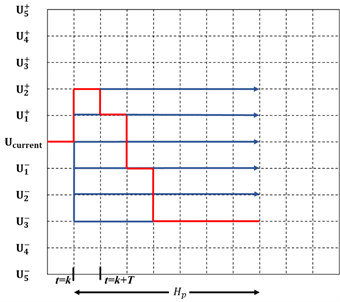
Fig. 3: MPC operation using multi-step ORE with four steps forward (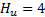 ). In red the optimal control action sequence found after optimization executed.
). In red the optimal control action sequence found after optimization executed.
Multi-step ahead approach to implement ORE suffers of the curse of dimensionality. For example, trying 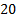 possible control sequences with three-step ahead control horizon, the number of option to be tested is
possible control sequences with three-step ahead control horizon, the number of option to be tested is 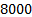 control actions combinations. Obviously, this is very time consuming requiring strategies to reduce that explosion of options to be tested. Among that strategies, the most easy to use and enough effective to reduce the number of combinations is to propose valve movements favoring the process error reduction. In that way a half of options is immediately reduced. If the same criterion is applied over the future errors detected by prediction with the model into the prediction horizon, a bigger reduction in the options to be tested is reached. That strategy is the used here only to determine the time reduction in the optimization time during NMPC execution.
control actions combinations. Obviously, this is very time consuming requiring strategies to reduce that explosion of options to be tested. Among that strategies, the most easy to use and enough effective to reduce the number of combinations is to propose valve movements favoring the process error reduction. In that way a half of options is immediately reduced. If the same criterion is applied over the future errors detected by prediction with the model into the prediction horizon, a bigger reduction in the options to be tested is reached. That strategy is the used here only to determine the time reduction in the optimization time during NMPC execution.
4. Illustrative case study
Currently, most of the industries deal with a changing market which is difficult to predict. The consumers demand better characteristics and specifications of products, while the companies try to improve performance and profitability indexes. In addition, the processing of agricultural commodities implies the variability of raw materials regarding the interesting compound. In spite of these situations, the final product must have the same quality. For this purpose, it is necessary to implement advanced control strategies for industrial processes that operate at multiple operating points and achieve optimal conditions.
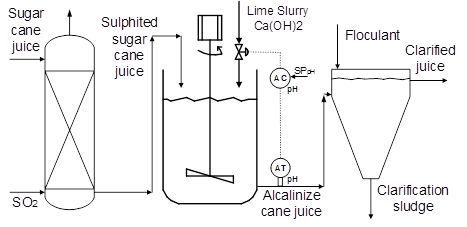
The case study considered in this work corresponds to the pH control of sugar cane juice in the sugar industry. pH is an important variable to be tracked in order to keep the standard of final sugar. The aim is to control the pH in the alkalinization section of a sugar cane plant. Alkalinization is a part of juice clarification sub-process, but affecting subsequently processes as evaporation and crystallization. During alkalinization, the juice is added with a lime slurry to compensate the pH after sulphitation process, as it is illustrated in Figure 4. The purpose of this process is to neutralize the juice to 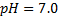 dealing with the highly nonlinear and complex dynamics inherent to pH variable. Note that these facts difficult the use of conventional control systems as PID.
dealing with the highly nonlinear and complex dynamics inherent to pH variable. Note that these facts difficult the use of conventional control systems as PID.
For controlling this process, it is used the phenomenological based semi-physical model (PBSM) developed in (Isaza & Alvarez, 2011) for the alkalinization stage of the sugar cane plant La Unión S.A, located in Guatemala. In this model, the variables are classified as follows: the controlled variable is the pH of the alkalized juice, the manipulated variable is the flow of lime slurry, also called whitewash, and the most common disturbances in the process are the flow of sulphited juice, the pH of sulphited juice and the pH of lime slurry, which changes with the aging of the slurry. Table 1 shows the operating ranges of the variables involved in the process.
For the simulation study, three disturbances are considered: the reduction in the flow of sulphited juice at 1 minute after beginning at stationary state, the reduction in the pH of sulphited juice at 6 minutes, and the increase of pH of lime slurry at 12 minutes, as shown in Figure 5. These disturbances are commonly found at the sugar cane clarification process in the real plant. This fact justify their use here.
Table 1 Variables classification and operation conditions of alkalinization section of a sugar cane plant.
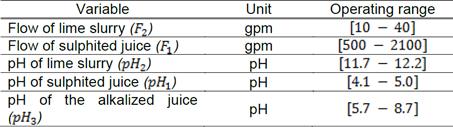
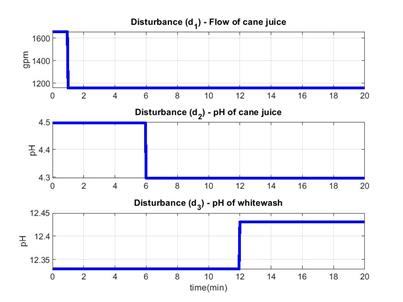
Fig. 5: Disturbances applied over the process: flow of sulphited juice, the pH of sulphited juice and the pH of lime slurry.
In order to reject these disturbances, a PID controller tuned using the technique presented in (Isaza & Alvarez, 2011) is used as the first option (the initially installed in that process). The performance of this controller faced with mentioned disturbances is shown in Figure 6. The pH behavior is oscillatory without stay over the set point during all the time. The disturbances effect is immediately reflected on pH as changes on oscillation amplitude. In the same way, the final control element output is oscillatory too, causing high mechanical stress to the valve dosing the lime slurry. It should be highlighted that negative flows of lime slurry were accepted in simulation to maintain unchanged the simulation program. Obviously, an IF structure put in the code conduce to the saturation of controller output at 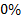 with the real consideration of those flow conditions are unfeasible in a real process. Several tuning alternatives where tested to improve the PID response, being the presented in this figures the best one obtained, indicating that Derivative effect is put in the control at its lower value (0.016), only to maintain the full PID structure. In addition a filtering of the pH signal is applied to reproduce the built-in electronic filter of the used pH transmitter (Hanna Instruments).
with the real consideration of those flow conditions are unfeasible in a real process. Several tuning alternatives where tested to improve the PID response, being the presented in this figures the best one obtained, indicating that Derivative effect is put in the control at its lower value (0.016), only to maintain the full PID structure. In addition a filtering of the pH signal is applied to reproduce the built-in electronic filter of the used pH transmitter (Hanna Instruments).
As it can be seen, the PID response is poor due to its inability to predict the typical abrupt changes on pH response, totally caused by the strong nonlinear behavior of this variable when small disturbances appear. That poor response of PID loop leads to think in using a NMPC as a feasible strategy to improve the pH control performance. Here, a NMPC strategy using the optimization algorithm proposed in this work, namely ORE, is illustrated. In spite of proofs with ORE using control horizon greater than 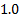 , the simulation results presented here are for control horizon of
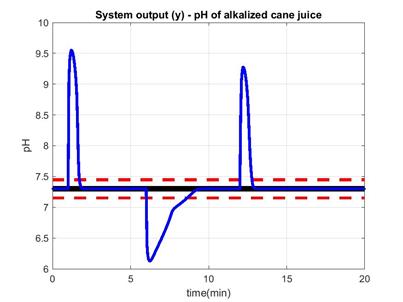
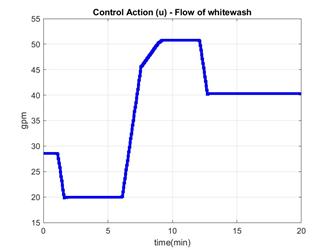
, the simulation results presented here are for control horizon of 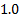 . The nonlinear PBSM is used not only as the predictor for the NMPC but also to simulate the process response. This is not a limitation because the model is used in its complete version or with all its nonlinear characteristics in both tasks. Figures 7 and 8 correspond to the pH variable and the movements of the valve dosing the lime slurry or whitewash flow, respectively, both using the NMPC using ORE with control horizon equal to
. The nonlinear PBSM is used not only as the predictor for the NMPC but also to simulate the process response. This is not a limitation because the model is used in its complete version or with all its nonlinear characteristics in both tasks. Figures 7 and 8 correspond to the pH variable and the movements of the valve dosing the lime slurry or whitewash flow, respectively, both using the NMPC using ORE with control horizon equal to 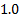 .
.
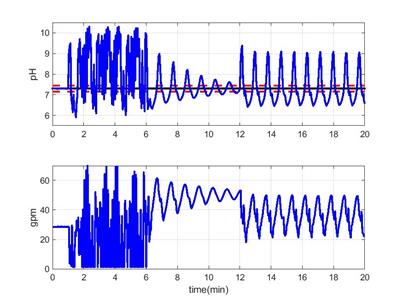
Fig. 6: Time evolution of pH and control variable for the alkalinization section of a sugar cane plant.
It is evident the better response of the process when the NMPC is used compare to PID response. The pH behavior is less oscillatory with only the typical overshoot produced by the first effect of disturbance. After that, the prediction ability of the NMPC compensates the disturbance long term effect maintaining the pH at the stated set point (SP). The final control element (FCE) movements are smooth and sequentially reached, due to the optimization by restricted enumeration used to solve the optimization problem of NMPC. The evident conclusion is the small mechanical stress to which the control valve is subjected. This fact, in addition to the better controlled response indicates the superiority of the NMPC over conventional PID control strategy, as it is expected. The ideal situation is to compare the current proposal with an industrial MPC structure. However, here the comparison was done regarding a PID controller because this kind of controller is the current one installed in the real process.
Regarding computational cost of NMPC solved with ORE vs. NMPC solved with known optimization algorithms, a test was done indicating a reduction of near to 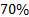 of computational cost for optimization executed using Matlab code. This results is for ORE with only one-step ahead or control horizon equal to
of computational cost for optimization executed using Matlab code. This results is for ORE with only one-step ahead or control horizon equal to 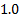 . For control horizon of three, the reduction in computation time is less significant, being of only
. For control horizon of three, the reduction in computation time is less significant, being of only 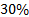 . However, using a control horizon of
. However, using a control horizon of 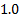 the performance of NMPC is the presented in previous results, which is enough to prefer ORE regarding other optimization approaches. In addition, the program to execute ORE with one-step ahead is as simple as it could be written with little lines of code in typical PLC platform. Its main characteristic is the absence of elaborated calculations to execute the optimization with the only requirement of solving the nonlinear PBSM of the process for different input or control action values. In that sense, other option is to convert the PBSM in format of differential and algebraic equations to a fuzzy inference systems, particularly Takagi-Sugeno as it is illustrated in (Isaza & Alvarez, 2011). Using that approach, the computation time is drastically reduced because to solve a Takagi-Sugeno FIS only require the basic mathematical operations. All these facts indicate the high applicability of ORE at industrial environments when the computational hardware is limited.
the performance of NMPC is the presented in previous results, which is enough to prefer ORE regarding other optimization approaches. In addition, the program to execute ORE with one-step ahead is as simple as it could be written with little lines of code in typical PLC platform. Its main characteristic is the absence of elaborated calculations to execute the optimization with the only requirement of solving the nonlinear PBSM of the process for different input or control action values. In that sense, other option is to convert the PBSM in format of differential and algebraic equations to a fuzzy inference systems, particularly Takagi-Sugeno as it is illustrated in (Isaza & Alvarez, 2011). Using that approach, the computation time is drastically reduced because to solve a Takagi-Sugeno FIS only require the basic mathematical operations. All these facts indicate the high applicability of ORE at industrial environments when the computational hardware is limited.
5. Conclusions
The main restriction of the industrial use of advanced control techniques is the complexity and robustness of their algorithms. From the practical point of view, the optimization by restricted enumeration (ORE) method was implemented showing feasible results. However, the most important contribution of the ORE method is its algorithmic simplicity, which is easily programmable in industrial control equipment such as a PLC. Thus, industrial implementation of advanced control techniques based on optimization is enhanced.
As a future work to extend the control horizon for multi-steps ORE, the number of possible combinations that this method requires to solve the optimization problem must be reduced. A predictive controller with enough dynamic information of the near future of the plant will have more possibilities to correct errors or future disturbances. In other words, it is not the same to excite the prediction model once and to keep the control action value during the prediction horizon, than to excite the model with a variable control action, which allows the model to exhibit dynamic characteristics of interest such that there is greater predictability on future plant behavior.