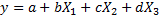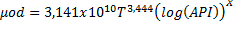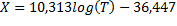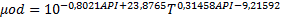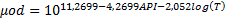1. Introducción
Los fluidos reales son viscosos, tienen fuerzas internas atractivas entre las moléculas de manera que cualquier movimiento relativo de las moléculas da como resultado fuerzas de fricción o de arrastre. El trabajo hecho por estas fuerzas de arrastre, a su vez, produce una pérdida de energía mecánica debido a un ligero calentamiento, lo que induce la resistencia al flujo. La viscosidad puede expresarse como viscosidad dinámica o viscosidad cinemática. La viscosidad dinámica es una medida de como se comporta un fluido respecto al esfuerzo de corte generado por presión y se mide en centipoise (cP) y la viscosidad cinemática se refiere a como se comporta el fluido ante la fuerza de gravedad y se mide en centistokes (cSt), (Swissoil, 2012).
La viscosidad de los petróleos pesados y extrapesados puede fluctuar entre menos de 20 cP y más de 1,000,000 cP (Alboudwarej et al, 2006). Esta característica de viscosidad hace que los mismos sean más difíciles de manejar y transportar a través de las tuberías, lo que hace que la determinación de esta propiedad sea de gran importancia para predecir su comportamiento. Se han establecido diferentes modelos matemáticos para la predicción de la viscosidad del petróleo muerto o libre de gas y entre ellas existen algunas aplicables a de grado pesados (Alomair et al, 2016; Naseri et al, 2005; Bennison, 1998; Glaso, 1980).
La mayoría de los modelos matemáticos desarrollados hasta el momento solo toman en cuenta como variables predictoras: la gravedad API y la temperatura, lo cual deja fuera de las ecuaciones algún parámetro que relacione la viscosidad con la composición del petróleo, lo que las hace limitadas a la muestra con que fueron obtenidas y de poca aplicabilidad a una población mayor. Por lo anterior se propuso la creación de un modelo matemático a ser aplicado a los petróleos pesados producidos en los Campos del Estado Monagas, Venezuela que tome en cuenta además de las dos variables predictoras mencionadas, el porcentaje de asfaltenos como variable predictora relacionada con la composición del petróleo. Las elevadas viscosidades de este tipo de crudos se debe a la complejidad de los asfaltenos. Cualquier forma que limite el entrelazado de los asfaltenos probablemente reducirá la viscosidad. Modificaciones del estado inicial de la agregación de asfaltenos, pueden influir en las propiedades del sistema principalmente en su viscosidad (Argillier et al, 2001) La relación entre la viscosidad del petróleo y el contenido de asfaltenos también fue estudiada por Evdokimov (2010) quien concluye que el análisis de las bases de datos de petróleo crudo revela un pico múltiple de viscosidad (hasta dos órdenes de magnitud) con contenidos de asfaltenos específicos, cerca de los límites de fase estructural observados en asfaltenos y soluciones de petróleo.
Modelos matemáticos como el de Ng y Egbogah (1983) incluyen como parámetro relacionado con la composición el punto de fluidez del petróleo, demostrando que la inclusión del mismo mejora la predicción al introducirlo en la ecuación de Beggs y Robinson como una propuesta de modificación. Otro modelo que incluye una variable relacionada con la composición del petróleo, fue propuesto por Naji (2011) en donde se incluye el factor de caracterización de Watson (Kw), el cual es un factor que proporciona un medio para identificar el contenido de parafinas o composición del petróleo crudo. Se mantiene razonablemente constante para los hidrocarburos químicamente similares.
En esta investigación se plantea el uso de modelos matemáticos ya establecidos para la predicción de la viscosidad de las muestras de petróleo pesado recolectadas y luego el análisis del comportamiento de la viscosidad respecto a cada variable predictora mediante métodos estadísticos para crear una ecuación propia que se ajuste a las características de la muestra y su comparación con los modelos ya existentes.
2. Metodología
Para el desarrollo de la investigación, en primer lugar se recolectaron 25 muestras de petróleo crudo pesado de los Campos productores del Estado Monagas Venezuela, específicamente de los campos Morichal, Jobo y Orocual, pertenecientes a la cuenca petrolífera oriental, en la cual se encuentran yacimientos de petróleo liviano, mediano y pesado. Las muestras fueron desgasificadas por lo que se consideran petróleo muerto. Las muestras fueron caracterizadas de acuerdo con su gravedad API aplicando el método del hidrómetro según procedimiento establecido en la norma ASTM D287, porcentaje de asfaltenos por precipitación con n-heptano de acuerdo con lo establecido en la norma ASTM D6560 y viscosidad dinámica mediante un viscosímetro Brookfield según el procedimiento descrito en la norma ASTM D2196. La viscosidad fue determinada a cinco (5) temperaturas: 23, 26, 30, 35 y 40 ºC.
Una vez obtenidos los datos necesarios para el desarrollo del modelo, se introdujeron en el paquete estadístico Statgraphics Centurion XVI que es un software estadístico de carácter privativo y uno de los más intuitivos para Windows. StatGraphics Centurión XVI es la décimo quinta edición de StatGraphics para computadores creado en 1980 por el Dr. Dr. Neil Polhemus, profesor de estadística de la Universidad de Princeton. Este software cuenta con una amplia gama de procedimientos (alrededor de 180) para el desarrollo de análisis estadísticos profundos de datos. Estos procedimientos abarcan desde resúmenes estadísticos hasta la elaboración de experimentos (Monterrosa, 2014). Con el Statgraphics Centurion XVI, se obtuvo en primer lugar la matriz de correlación entre las variables tomando como parámetros el valor-p del análisis ANOVA con nivel de significancia un α = 0,05 y el coeficiente de correlación de Pearson (R). El objetivo de la matriz de correlación fue hallar la relación lineal entre las variables según los criterios establecidos por Beldjazia y Alatou, (2016) los cuales se muestran en la Tabla 1.
Se establecieron dos modelos matemáticos: lineal múltiple y no lineal múltiple.
Tabla 1 Criterios de correlación
| Coeficiente de correlación R | Significado |
| 0 - 0,19 | Muy débil |
| 0,20 - 0,39 | Débil |
| 0,40 - 0,59 | Moderada |
| 0,60 - 0,79 | Fuerte |
| 0,80 - 1,00 | Muy fuerte |
2.1. Modelo lineal múltiple
Se utilizó la opción de regresión lineal múltiple del paquete estadístico, en el cual se aplica el método de mínimos cuadrados ordinarios para establecer los coeficientes de la ecuación 1 de la forma:
donde:
y = Viscosidad dinámica, cP
X1 = Temperatura, ºC
X2 = Gravedad API
X3 = Porcentaje de asfaltenos
a, b, c y d = Coeficientes de la ecuación
El modelo obtenido fue evaluado tomando en cuenta el coeficiente de determinación R2 y el error relativo medio (ERM). También se analizó gráficamente el comportamiento de los valores predichos por el modelo respecto a los valores medidos.
2.2. Modelo no lineal múltiple
Para el establecimiento de este modelo, se analizó por separado el comportamiento de la Viscosidad respecto a cada una de las variables predictoras de manera individual mediante análisis de regresión simple. Se utilizó la opción de modelos de regresión simple alternativos del paquete estadístico, escogiéndose para cada variable predictora el comportamiento con el mayor R y con Valor-p < 0,05.
Una vez establecida la relación entre las variables se estableció el modelo matemático y se cargó en la opción de regresión múltiple no lineal del paquete estadístico, con lo que se determinaron los coeficientes del modelo, mediante el método Marquardt con nivel de confianza de 95%, valor inicial de 1, factor de escala de 20, valor máximo de 1200 y número máximo de iteraciones de 1000.
El modelo matemático se validó respecto al coeficiente de determinación R2 y el error relativo medio (ERM)
2.3. Comparación de los modelos establecidos con modelos existentes
Luego del desarrollo de los modelos se procedió a comparar los resultados obtenidos con modelos existentes aplicables a petróleo pesado muerto, los mismos fueron:
Modelo de Glasoecuación 2
con T en ºF
Modelo de Bennisonecuación 4
con T en ºF
Modelo de Naseri et alecuación 5
con T en ºF
Además de los modelos establecidos los cuales incluyen el porcentaje de asfaltenos como variable predictora adicional, se tomaron en cuenta dos modelos adicionales solo con las variables API y Temperatura para comparar respecto a las mismas condiciones de los modelos existentes y comprobar la mejora en la predicción al incluir la tercera variable predictora. A cada modelo se le determinó el ERM como parámetro de comparación y validación.
3. Resultados y discusión
Los resultados corresponden principalmente a la caracterización de las muestras de petróleo pesado muerto utilizadas para el desarrollo del modelo matemático.
En la Tabla 2 se muestran los diferentes rangos obtenidos para cada una de las variables del modelo matemático a desarrollar, una vez aplicados los diferentes ensayos de laboratorio para su obtención.
Los valores a API son más bajos que los utilizados en el desarrollo de otros modelos como el de Glaso (1980) cuyos valores estuvieron entre 20 y 48 API; Bennison (1998) para API mayores a 20 y Naseri et al (2005) con valores entre 17 y 44 API. En cuanto al rango de temperatura establecido, el mismo estuvo dentro de los rangos del modelo de Glaso (10 - 149 ºC) pero fuera de los rangos establecidos para los modelos de Bennison (>121 ºC) y Naseri t al (40 - 146 ºC). Los rangos de viscosidad para el modelo propuesto en esta investigación fueron mayores a los de los modelos de Glaso (0,6 - 39 cP) y Naseri et al (0,75 - 54cP) y menores al rango de viscosidad del modelo de Bennison (> 100 cP). La diferencia entre los rangos de aplicabilidad del modelo propuesto y los modelos existentes influye de manera importante en los resultados obtenidos, respecto al posible ERM que se determine al aplicar cada una de los modelos matemáticos.
Tabla 2 Características de las muestras
| Variable | Rango |
|---|---|
| API | 11,1 - 21,6 |
| %ASF | 5,8 - 12,4 |
| T , ºC | 23 - 40 |
| μod, cP | 62,1 - 376,0 |
Otros modelos como el de Alomair et al (2016) presentan rangos de API y Temperatura que corresponden a los utilizados en la presente investigación ( API de 11,7 a 18 y Temperaturas entre 20 y 160 ºC); sin embargo, este modelo no se pudo utilizar como comparación, pues el mismo tiene como variable predictora adicional el punto de fluidez, valor que no estaba disponible para la realización del modelo matemático propuesto.
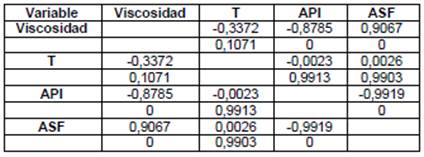
En la Tabla 3 se muestran los resultados de la matriz de correlación, en ella se observa el valor superior que corresponde al coeficiente de correlación de Pearson (R) y en la fila inferior el Valor- P del análisis ANOVA con valores estadisticamente significativos para Valor-P < 0,05.
De acuerdo con la matriz de correlaciones, existe una relación estadística muy fuerte entre la Viscosidad y las variables API y ASF (Beldjazia y Alatou, 2016). Observándose además que la variable Temperatura se relaciona de forma moderada con la Viscosidad. Según el coeficiente R, la Viscosidad varía de forma inversa con la temperatura y la API y de forma directa con el porcentaje de asfaltenos.
El Valor-P muestra que existe una relación estadísticamente significativa entre la Viscosidad y las variables API y ASF (Valor-P < 0,05); sin embargo, se muestra que no existe relación significativa entre la Viscosidad y la Temperatura (Valor-P > 0,05). Se sabe que la Viscosidad de los líquidos es influenciada de manera determinante por la temperatura, pero esta relación no es lineal, como lo mencionan Knežević y Savić (2006) existen varias ecuaciones que relacionan a la Viscosidad con la Temperatura, todas ellas con tendencias no lineales, entre ellas la más precisa es la ecuación de Vogel, la cual es exponencial. Dado que el coeficiente de correlación de Pearson es un parámetro que mide la relación lineal entre dos variables, se puede decir entonces que el resultado obtenido es lógico debido a que no existe correlación lineal fuerte entre la Viscosidad y la Temperatura, sino como lo indica la matriz de correlaciones, moderada.
La matriz de correlaciones también muestra que existe correlación muy fuerte entre las variables API y ASF, lo que es un indicativo de colinealidad entre ellas. Esto puede sugerir la eliminación de una de las variables del modelo; sin embargo, en este trabajo se dejaron todas las variables para ver si en el desarrollo de los modelos matemáticos algún parámetro estadístico sugiere la simplificación de los mismos eliminando alguna de las dos variables relacionadas.
3.1. Modelo lineal múltiple
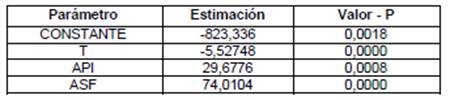
En la Tabla 4 se muestran los coeficientes obtenidos para la ecuación 1 descrita en el punto 2.1, de la ecuación lineal múltiple, así como el Valor-P, el cual representa la significancia estadística de cada uno de los coeficientes para α = 0,05.
Se observa que todos los valores de los coeficientes obtenidos son significativos (Valor-P < 0,05) lo cual indica que todas las variables predictoras influyen de manera significativa en el modelo matemático; el coeficiente con el mayor Valor-P está en la Constante (A) con 0,00018. Los valores obtenidos indican, al igual que la matriz de correlaciones que la variable más influyente es el porcentaje de asfaltenos (ASF), resultado que está acorde con lo expresado por Sattarin, et al (2007) en el cual se menciona que los componentes pesados polares (Resinas y Asfaltenos) tienen gran influencia sobre la predicción de la viscosidad en petróleos pesados.
3.2. Modelo no lineal múltiple
En la Tabla 5 se muestran las ecuaciones de regresión simple que relacionan a la viscosidad con cada una de las variables predictoras de manera individual, además del coeficiente de correlación no lineal para establecer el grado de relación entre las variables.
Se observa que la relación entre la Viscosidad y las tres variables predictoras es de tipo exponencial; en todos los casos la correlación es muy fuerte (>0,9). La temperatura se muestra como la variable predictora de mayor influencia a diferencia de lo obtenido en el modelo lineal múltiple, esto es concordante con Knežević y Savić (2006), además el modelo de regresión exponencial es coincidente con la ecuación de Vogel mencionada por estos autores. La segunda variable en importancia fue el porcentaje de asfaltenos, el cual influye de manera proporcional sobre la viscosidad. Al ser los asfaltenos hidrocarburos complejos, la mayor cantidad de estos en el petróleo genera un aumento en la viscosidad; al respecto Jaramillo (2007) menciona que los líquidos tienden a ser más viscosos tanto como aumenta el tamaño de las moléculas que lo componen o como aumenta la vinculación intermolecular entre las partículas. Márquez et al (2006) al estudiar la influencia de los asfaltenos y las resinas sobre el comportamiento de la viscosidad de petróleo pesado concluye que la alta viscosidad se explica fundamentalmente por la presencia de asfaltenos que además la presencia de resinas contribuye esta dependencia.
Tabla 5 Modelos de regresión simple entre viscosidad y las variables predictoras
| Modelo | Ecuación | Correlación |
|---|---|---|
| Viscosidad versus T | μod = e(a+b*T) | -0,9991 |
| Viscosidad versus API | μod = e(a+b*API) | -0,9173 |
| Viscosidad versus ASF | μod = e(a+b/ASF) | 0,9427 |
La influencia de la API sobre la Viscosidad se muestra como la de menor importancia entre las variables predictoras; sin embargo, su correlación muy fuerte indica su importancia como variable predictora. Al igual que para las otras dos variables predictoras, la API se relaciona de forma directa y exponencial con la viscosidad; este es el comportamiento esperado al observar modelos matemáticos existentes en los cuales existe este tipo de modelo de regresión entre las variables mencionadas,
3.3. Modelos propuestos
En la Tabla 6 se muestran los dos modelos matemáticos obtenidos en la investigación, así como los coeficientes de determinación R2 de cada uno, lo que expresa que tanto predice cada modelo la variabilidad de la viscosidad.
Tabla 6 Modelos matemáticos establecidos
| Modelo | Ecuación | R 2 |
| Lineal múltiple | μod = -823,336 - 5,52748*T + 29,6776*API + 74,0104*ASF | 0,9647 |
| No lineal múltiple | μod = e (2,47067-0,0297729*T) *e (2,47067 +0,0680858*API) *e (2,47067 + -21,2865/(ASF)) | 0,9792 |
Se observa que ambas ecuaciones tienen un coeficiente de determinación similar, lo que indica que predicen la variabilidad de la Viscosidad en más de 95%, en el caso del modelo lineal múltiple en 96,47% y el no lineal múltiple en 97,92%. Un análisis ANOVA realizado a los coeficientes de determinación mostró que no existe diferencia significativa entre ellos, por lo que la selección del modelo a proponer va a depender del valor de ERM obtenido para cada uno.
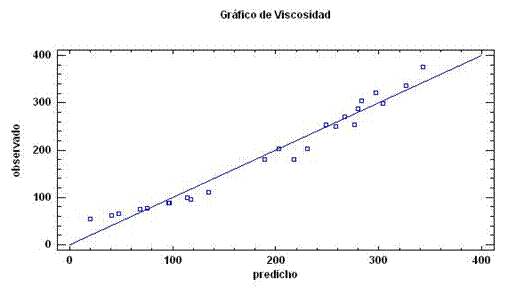
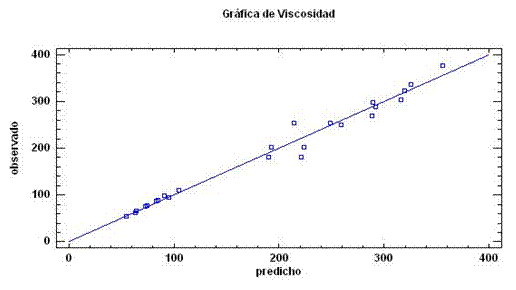
Las figuras 1 y 2 muestran los gráficos cruzados correspondientes a cada uno de los modelos matemáticos obtenidos.
Las figuras 1 y 2 representan la relación lineal entre los valores predichos por los modelos establecidos y los valores observados en los ensayos de laboratorio. Son una representación gráfica del ajuste de los valores experimentales y los predichos. Gráficamente se observa que en la figura 1, los valores predichos de Viscosidad se ajustan mejor para valores mayores a 200 cP y para los valores menores de Viscosidad el comportamiento de la predicción es menos ajustada. En el caso de la figura 2, se observa un resultado contrario, los mejores ajustes en los valores predichos son para valores de Viscosidad menores a 1200 cP, notándose una mayor dispersión de los puntos para los valores mayores a 200 cP. A pesar de las diferencias en el comportamiento de los gráficos cruzados, la figura 2 muestra un mejor ajuste de los valores predichos respecto a los observados, concordante con el mayor coeficiente R2 del modelo no lineal múltiple.
En la Tabla 7 se muestra la comparación en función al ERM entre los modelos establecidos en la investigación y otros tres (3) modelos existentes utilizados para predecir la viscosidad de petróleo pesado muerto, para definir la aplicabilidad de los modelos a las muestras utilizadas.
Tabla 7 Comparación entre modelos matemáticos
| Modelo | ERM (%) |
|---|---|
| Glaso | 35,5 |
| Bennison | 107,5 |
| Naseri | 61,7 |
| Lineal múltiple con ASF | 12,70 |
| No lineal múltiple con ASF | 5,05 |
| Lineal múltiple sin ASF | 17,03 |
| No lineal múltiple sin ASF | 19,13 |
Se observa claramente cómo los modelos propuestos superan a los modelos tomados como referencia para la predicción de la Viscosidad aplicados a las muestras en estudio. De los modelos existentes y de común aplicación en la industria petrolera, el que mejor comportamiento mostró fue el de Glaso; sin embargo, al compararlo con los modelos propuestos, estos lo superaron ampliamente. También se puede observar como la inclusión de la variable ASF al modelo genera un menor porcentaje de error respecto a los valores experimentales en comparación con los modelos sin esta variable, lo que es más evidente en el modelo no lineal múltiple, en el que la presencia de la variable ASF disminuye el ERM en 14,08 puntos porcentuales en comparación con los 4,33 puntos porcentuales que disminuye el modelo lineal múltiple. Lo anterior sugiere que el modelo matemático no lineal es influenciado de manera más significativa por la variable ASF y que la misma no puede ser eliminada del mismo. En el caso del modelo lineal múltiple, la presencia de la variable ASF no modifica en gran medida los resultados, lo que lo hace un modelo más estable.
3. Conclusiones y recomendaciones
Los modelos matemáticos obtenidos en esta investigación son aplicables a los petróleos pesados muertos producidos en el Estado Monagas Venezuela; el modelo no lineal múltiple es el recomendado por presentar el mayor coeficiente de determinación R2 de 0,9792 y un error relativo medio de 5,04%
Los dos modelos propuestos en este estudio superaron en aplicabilidad a los modelos existentes tomados como comparación, a saber Glaso, Bennison y Naseri et al mostrando porcentajes de error relativo medio inferiores.
La inclusión de la variable porcentaje de asfaltenos (ASF) en los modelos matemáticos propuestos fue determinante en la predicción de la viscosidad, disminuyendo el porcentaje de error relativo medio en ambos.
En caso de contarse con todas las variables involucradas en la predicción, es claro que el modelo no lineal múltiple debe ser el modelo seleccionado; sin embargo, de no contarse con la variable porcentaje de asfaltenos, se recomienda el uso del modelo lineal múltiple.
Se recomienda aplicar la metodología utilizada en esta investigación a muestras de petróleos muertos livianos y medianos producidos en el Estado Monagas Venezuela, con la finalidad de establecer modelos matemáticos para predecir la Viscosidad de todos los petróleos producidos en la zona.
Ampliar el estudio a la predicción de la viscosidad para petróleos con gas a condiciones de yacimiento (saturado y subsaturado)