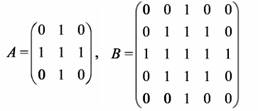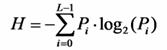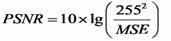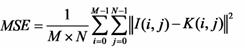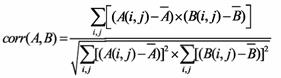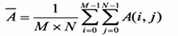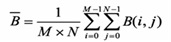1. Introducción
Los bordes se definen, en términos de procesamiento de imágenes digitales, como los lugares donde se produce un fuerte cambio de intensidad. Las técnicas de detección de bordes se requieren a menudo en diferentes tareas de procesamiento de imágenes y visión por ordenador , para la segmentación de imágenes, el reconocimiento de patrones, preservar importantes propiedades estructurales, etc. Estas tareas son aplicadas a áreas tales como la teledetección, la medicina, entre otras.
El proceso de detección de bordes sirve para simplificar el análisis de las imágenes reduciendo drásticamente la cantidad de datos a procesar, al mismo tiempo permite preservar la información estructural útil sobre las fronteras del objeto. Ciertamente hay una gran diversidad de aplicaciones para la detección de bordes, pero se considera que muchas de éstas aplicaciones comparten un conjunto común de requisitos entre ellos tener una baja tasa de error en el proceso de detección (Canny, 1986)
A lo largo de las últimas décadas se han propuesto distintas técnicas para la detección de bordes, por ejemplo, en (Ma, Gao, Yang, & Liu, 2010) se propone la detección de bordes mediante la aproximación de máscaras circulares y asociando cada punto de la imagen con un área local de brillo similar. El principal inconveniente de esa propuesta es la alta sensibilidad al ruido y la poca capacidad para discriminar bordes frente a texturas. Además, su precisión no es completamente robusta debido a la dependencia del parámetro de la desviación estándar del filtro gaussiano que se utiliza para la eliminación del ruido, el cual se selecciona de forma manual, lo que conlleva a pérdidas en la precisión de los resultados. Debido a estas limitaciones se ha propuesto la inclusión de filtros morfológicos que eliminan esta dependencia.
Las imágenes de diferentes espectros proporcionan el potencial para una extracción de información más precisa y detallada, de allí que, se han realizado estudios de imágenes proporcionadas por satélites para ser utilizadas en procesos de clasificación y medición de la exactitud de la resolución y características en las imágenes analizadas (Wilkinson., 2005). Se han realizado otros estudios basados en el reemplazo del filtro Gaussiano por otro adaptativo basado en la máxima probabilidad entre las clases y la medición de la entropía cruzada para obtener menor diferencia entre el fondo y los objetivos para obtener el nivel óptimo de los bordes (Wang & Wang, 2009). En dicho estudio se propone un método de dos etapas para la segmentación general de imágenes, que es capaz de procesar tanto objetos texturizados como no texturizados de una manera significativa.
También hay técnicas de detección de contornos, que calculan de forma adaptativa los umbrales de detección de borde basados en el tipo de bloque y la distribución local de los gradientes en el bloque de la imagen. (Xu, Varadarajan, Chakrabarti, & Karam, 2014). Así también se presentan técnicas basadas en la transformada de Shear que facilitan que los bordes direccionales sean más fáciles de detectar, con esto se mejora la calidad de los bordes detectados (Xu, Miao, Shi, Zhang, & Yang, 2012).
Algunas propuestas para análisis de imágenes de diferentes espectros se han realizado mediante la segmentación, es decir dividir una imagen en regiones disjuntas, de manera coherente con la percepción humana del contenido. Sin embargo, para la segmentación sin supervisión de imágenes generales, existe el requisito de no hacer suposiciones previas sobre la escena (O'Callaghan, Robert, & Bull., 2005). Por lo general, las aplicaciones de tele-observación cross-espectral o multiespectral, se aplican en proyectos que tienen alguno de los siguientes objetivos: Detección de objetivos (tumores, objetos, personas, etc.), mapeo de materiales, seguimiento, clasificación, segmentación, mapeo de las propiedades de las superficies para la identificación de materiales, etc (Pohl & Van, 1998 ). Cross-espectral se refiere a imágenes de sólo dos bandas, mientras que multiespectral se trata de imágenes de más de 2 bandas.
Considerando la importancia de analizar este tipo de imágenes cross-espectrales, es que se considera oportuno innovar con nuevas técnicas que permitan utilizar imágenes de espectro infrarrojo, de tal forma que se obtenga una mayor precisión en la detección de bordes. Por ello la importancia de definir métricas que nos permitan medir la calidad de los datos y resultados, para lo cual usaremos GQM.
Este artículo contribuye a:
Mejorar la detección de bordes en imágenes cross-espectrales haciendo uso de una variación de los filtros morfológicos propuestos en (Deng, Wang, & Yang, 2013).
Utilizar la metodología GQM para definir un proceso estructurado de evaluación de la calidad del pre-procesamiento de las imágenes a utilizar en los experimentos.
El resto del artículo está organizado como sigue, la sección II contiene el marco teórico, donde se describe el modelo GQM y el enfoque matemático del problema. La sección III presenta la metodología, donde se define el método de investigación, la selección y la preparación de los datos, el diseño del experimento, los experimentos, la sección IV que presenta el análisis de los resultados, y finalmente la sección V con las conclusiones del estudio.
2.- Marco Teórico
2.1 Enfoque GQM.
GQM es un mecanismo que provee un marco para definir un programa de métricas, fue diseñado en la universidad de Maryland como un mecanismo para formalizar las tareas de caracterización, planeación, análisis, aprendizaje y retroalimentación (Van Solingen, Basili, Caldiera, & Rombach, 2002). GQM no provee objetivos específicos, sino más bien un marco de trabajo que plantea los objetivos de medición y se los refina con preguntas para proveer una especificación más clara de los datos que se necesitan para alcanzar los objetivos planteados.
Originalmente desarrollado por V. Basili y D. Weiss, y ampliado con muchos otros conceptos de D. Rombach. GQM es el resultado de muchos años de experiencia práctica e investigación académica. GQM contiene cuatro fases: Planificación, Definición, Recolección e Interpretación de las mediciones. Utilizando GQM se han propuesto por ejemplo, modelos para monitorear los factores de éxito en la implementación de proyectos de sistemas ERP lo cual sirve para un mejor soporte administrativo durante la implementación. (Esteves, Pastor-Collado, & Casanovas, 2002).
GQM también has sido utilizado en la construcción de un modelo de calidad aplicable a los sistemas de interacción Hombre-Máquina relacionados al campo de la medicina para medir los puntos de vista de los diferentes grupos de usuarios involucrados en los procesos en un hospital como por ejemplos los médicos, enfermeras, auxiliares, etc. Con esta información retroalimentada las instituciones médicas pueden mejorar los procesos y la calidad de la atención a los pacientes, con lo cual se aporta al bienestar común de la sociedad. (Al-Nanih, Al-Nuaim, & Ormandjieva, 2009).
Hay que considerar que es importante realizar la validación formal, empírica y la explicación filosófica de las métricas que se definan ussndo GQM. (Calero, Piattini, & Genero, 2001)
2.2 Enfoque Matemático del Problema.
Los sensores cross-espectrales permiten captar imágenes correspondientes a diferentes bandas del espectro, para una misma área en la superficie terrestre. Dado que diferentes materiales tienen características espectrales diferentes, dichas imágenes ofrecen una herramienta muy efectiva para discriminar y clasificar diferentes objetos. Sin embargo, existen varias dificultades a la hora de abordar el proceso de clasificación de imágenes cross-espectrales. Existen algunas técnicas de detección de características en imágenes 2-D, basadas en una óptima obtención de bordes que deben ser invariantes a factores de la escena; que se basan en los cambios bruscos de intensidades generados por discontinuidades en la superficie o por límites definidos por cambios en la reflectancia o iluminación en la imagen (Ma, Gao, Yang, & Liu, 2010), (Marr & Hildreth, 1980). También hay propuestas de detección de contornos basadas en la detección precisa de las formas en imágenes de dos dimensiones (2-D), obteniendo una función escalonada para modelar la sección transversal del contorno de la forma, derivando a una sola dimensión (1-D), que minimiza tanto el ruido como el error cuadrático medio entre la entrada y la salida del filtro utilizado (Rosenfeld, 1970).
Este trabajo explora el uso del espectro visible y el infrarrojo cercano (NIR) para la función de detección de los bordes en las imágenes. En particular, investigamos generalizaciones cross-espectrales del detector bordes Canny para mostrar que estos dan una marcada mejoría en el rendimiento cuando el canal de IRC adicional está disponible.
En la visión por computador, es necesario establecer puntos coincidentes entre diferentes imágenes, de tal forma que, al relacionarlas, podamos extraer información de las mismas y tomar acción sobre ellas. (Elder & Zucker, 1998). Cuando hablamos de puntos coincidentes nos referimos de manera general a las características de la escena que necesitamos reconocer de manera única y con facilidad. La mayoría de las imágenes se ven siempre afectadas por ruido, y una de las debilidades del algoritmo de Canny, es que hace uso del filtrado Gaussiano. Dicho filtro tiene la deficiencia de la adaptabilidad al tipo de ruido; por ende, se pudieran detectar bordes falsos o perder bordes, dado que el proceso de filtrado los ha removido.
Basados en el operador convencional del algoritmo de Canny y en muchas otras técnicas como la lógica difusa, la transformada Wavelet, control de escala lineal y filtrado morfológico o lineal sugeridos en los artículos de : (Patel, Dhiraj, Sagar, & More, 2013), (Xia, Yao, Chang, & Zhong, 2010), (Demigny, 2002), (Xu, Weaver, & Healy, 1994), (Heric & Zazula, 2007), (Elder & Zucker, 1998), nuestro artículo propone realizar una variación del filtro morfológico presentando en (Deng, Wang, & Yang, 2013), donde se reemplaza el filtro gaussiano que presenta la debilidad de la selección manual de la varianza para realizar la reducción del ruido. Este estudio utiliza en los experimentos imágenes cross-espectrales fusionadas para evaluar las variantes propuestas. La técnica utilizada por el algoritmo de Canny es la obtención de los bordes diferenciales, las fases se detallan a continuación:
- Filtrado
- Obtención de la magnitud y orientación del gradiente
- Supresión de los no máximos al resultado del gradiente.
- Umbralización con histéresis
El propósito del filtrado de una imagen es disminuir el ruido. Cuando se utiliza un filtro Gaussiano se debe escoger de forma manual el grado de amplitud del suavizado (la varianza σ) a aplicar a la imagen. Esto se puede considerar como una debilidad del proceso, ya que cada imagen puede tener tipos y niveles de ruido diferentes y por ende en ciertos casos se necesitará definir una varianza más alta o más baja. Si se deja de manera constante un mismo valor de varianza, se podrían perder los detalles de la imagen por tener valores muy altos, o en su defecto, poca reducción de ruido al utilizar valores muy bajos (Zue, Li, & Wang, 2010).
La morfología matemática es una técnica de procesamiento no lineal de la señal caracterizada para realzar la geometría y forma de los objetos (O'Callaghan, Robert, & Bull., 2005). El objetivo de las operaciones morfológicas es la extracción de figuras geométricas de los conjuntos sobre los que opera, dicha extracción se realiza mediante el uso de otro conjunto denominado, elemento estructurante, el tamaño y forma de este elemento se lo elige en función de la morfología que se desea aplicar y la obtención de la forma del elemento que se desea extraer. El elemento estructurante se desplaza de manera sistemática a través de toda la imagen a procesar, realizando cualquiera de las operaciones existentes, a saber: erosión, dilatación, apertura y cierre (Deng, Wang, & Yang, 2013).
De acuerdo a lo presentado en (Deng, Wang, & Yang, 2013), asumiendo una imagen F(x,y) en escala de grises y un elemento estructurante B(s,t), las operaciones básicas de morfología en escala de grises propuestas por el autor son :
Dilatación: F B=max{(F(x-s,y-t)+B(s,t)}
B=max{(F(x-s,y-t)+B(s,t)}
Erosión: FΘB=min{(F(x-s,y-t)-B(s,t)}
Su propuesta utiliza dos elementos estructurales tipo diamante, uno de 3 x 3 elementos y el otro una combinación de 5x5 elementos, los que se visualizan a continuación:
De tal forma, que la operación de filtrado de apertura-cierre de una imagen está dado por:
Fsinruido = (F o A) • B
El presente artículo propone un cambio en las operaciones morfológicas, puesto que se están utilizando imágenes cross- espectrales fusionadas las cuales contienen menos ruido. Por lo expuesto, se propone una variante en el tamaño y la geometría de los elementos estructurantes. Esta variante nos permite mantener la información del detalle de los bordes de las imágenes, al reducir la capacidad de eliminación de ruido, debido a que estamos utilizando imágenes cross-espectrales fusionadas. Los cambios propuestos se detallan a continuación:
1.- Cambiar el segundo elemento estructurante, diamante 5x5 por uno de 3x3 del mismo tipo.
2.- Realizar una nueva operación de filtrado, la cual consiste de apertura-cierre-dilatación aplicados a la imagen F(x,y), la misma que está dada por:
Esta propuesta permite mejorar la conservación de los detalles de la imagen, al reducir el kernel B a un tamaño de 3 x 3, generando un menor suavizado también, al cambiar el modelo morfológico, ya que se incluye una operación adicional de dilatación, se reducen los cambios de las altas frecuencias de la imagen, preservando la información de los cambios de intensidades de forma más homogénea reduciendo los bordes falsos positivos.
3. Metodología
3.1 Definición del Método de Investigación
De acuerdo a lo propuesto por Runkel y McGrath (1972). El presente trabajo utiliza el método de experimentos de laboratorio, utilizando métricas previamente definidas para el diseño experimental,
Se utilizaron métodos cuantitativos con el objetivo de probar o descartar la hipótesis planteada con respecto a la mejora en la calidad de la detección de bordes propuesta por Canny, Se estima una mejora debido a la utilización de filtros morfológicos, con imágenes cross-espectrales, que al tener una mayor entropía; son menos susceptibles al ruido, y se obtienen contornos con mayor precisión y menor cantidad de bordes falsos positivos.
El pre-procesado toma las imágenes de ambos espectros, y realiza la fusión de las mismas. El proceso de fusión consiste en reemplazar la información de un canal de la imagen visible por la imagen infrarroja. De las tres posibles combinaciones (R,G,NIR), (R,NIR,B) y (NIR,G,B) se selecciona la que genere la mayor varianza de intensidades. Para nuestro caso es: (NIR,G,B); donde NIR es infrarrojo cercano, R es red, G es Green y B es blue. Luego se ejecuta el algoritmo de Canny original y el propuesto con las variantes matemáticas, se miden los resultados obtenidos y se realiza el análisis comparativo.
3.2 Selección de datos
Los datos fueron obtenidos de la base de datos del laboratorio de Visión por Computador de la Universidad Politécnica Federal de Lausana. Esta base de datos consiste de 477 imágenes categorizadas en 9 grupos capturadas en RGB (Espectro Visible) y NIR (Near Infrared). Para este estudio utilizaremos las imágenes de la categoría “Urban”, debido a que las imágenes de dicha categoría son las más afectadas por condiciones de variación de iluminación y texturas lo cual incide de manera directa en la variabilidad y complejidad de la detección de los contornos de las imágenes y por ende se constituyen en los escenarios más propicios para la evaluación de la variante propuesta a nivel de los filtros morfológicos.
Se seleccionaron 150 pares de imágenes de dicha categoría para evaluar la detección de los contornos utilizando el algoritmo con la variante propuesta, junto con el original de Canny para obtener los resultados y efectuar la respectiva evaluación comparativa.
Fusión de Imágenes Cross-espectrales: Uso de GQM
Para realizar los experimentos de detección de bordes con imágenes cross-espectrales fusionadas es necesario: pre-procesar las imágenes para reducir el ruido, y mejorar la entropía determinando cual es la mejor combinación de canales del espectro que permitan obtener una imagen fusionada que genera la mayor varianza de intensidades de forma que se puedan obtener los bordes con mejor precisión.
En este estudio se definieron las siguientes metas para el pre-procesamiento de las imágenes:
1.- Reducir ruido de una imagen
2.- Fusionar imágenes de diferentes espectros
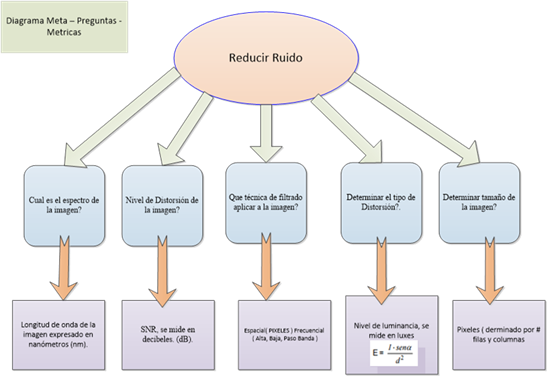
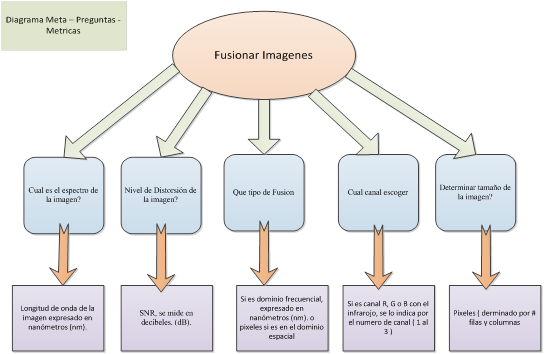
La siguiente etapa es definir las preguntas que van a recolectar la información cuantitativa, y luego determinar las métricas necesarias para preparar de la mejor forma las imágenes a procesar. Se pueden observar los modelos GQM planteados para cada una de las metas previamente descritas. Ver Figura 1 y Figura 2.
Para preparar las muestras de las imágenes fusionadas se realiza la separación de las bandas de las imágenes del espectro visible (R-rojo, V-verde, B- azul) y se fusiona con la imagen del espectro infrarrojo cercano. Aplicando el modelo GQM mostrado en la Figura 2, para la fusión de imágenes se obtienen las métricas que determinaron que la mejor entropía se logra con la combinación (NIR,G,B). Con lo cual es posible iniciar los experimentos y utilizar las imágenes fusionadas para la detección de los contornos de Canny modificado por las variantes morfológicas propuestas y comprobar así que existe una mejora de los resultados de la detección.
Un ejemplo de los resultados de las imágenes obtenidas con la fusión propuesta, (las que tienen la mejor entropía), se presenta en la Figura 3 (categoría “Urban”).
3.4 Experimentos
Durante los experimentos se ha ejecutado el algoritmo de Canny en su versión original con las 150 imágenes seleccionadas de la categoría “Urban”, pre-procesadas y fusionadas. Luego, con el mismo conjunto de imágenes, se ha ejecutado el algoritmo con la variación propuesta en este trabajo. Es decir, la utilización de los filtros morfológicos con un diseño diferente de los elementos estructurantes y la inclusión de los gradientes oblicuos sugeridos en (Deng, Wang, & Yang, 2013), sustituyendo el filtrado Gaussiano que tiene poca adaptabilidad al ruido. Los resultados obtenidos de ambos algoritmos han sido comparados de acuerdo a las métricas tomadas de (Deng, Wang, & Yang, 2013) y que se detallan a continuación:
La información de la probabilidad de la mejora de la calidad de los bordes de la imagen, es decir, el nivel de entropía, viene dado por la siguiente definición:
Donde, Pi, expresa la probabilidad de que los valores de los pixeles en una imagen en escala de grises sean iguales a i. Por ende, a mayor valor de entropía, mayor de información de los contornos de la imagen original se obtiene.
Otra métrica a utilizar es el PSNR, que son los picos de la relación señal-ruido en una imagen, la cual viene dada por:
Los coeficientes de correlación reflejan el grado de relevancia de las imágenes, la definición viene dada por:
Donde, 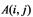 y
y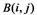 son los valores en escala de grises de las dos imágenes.
son los valores en escala de grises de las dos imágenes.
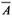 y
y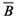 representan la media de los valores respectivamente. Mientras más cercano a 1 sea el coeficiente de correlación, mejor es el grado de aproximación que tiene la imagen.
representan la media de los valores respectivamente. Mientras más cercano a 1 sea el coeficiente de correlación, mejor es el grado de aproximación que tiene la imagen.
4. Resultados y Discusión
Se ha realizado un análisis cuantitativo de las métricas alcanzadas para demostrar que la precisión de los bordes obtenidos con las variantes propuestas utilizando imágenes Cross-espectrales fusionadas, es superior a los resultados obtenidos con el algoritmo de la versión original. Se puede visualizar los resultados obtenidos con las imágenes en la categoría “Urban” en tres escenarios diferentes: edificios, puertas y fachadas. Ver Figura 4. Comparaciones con la técnica presentada en (Deng, Wang, & Yang, 2013) no son adjuntadas dado que no se pudo encontrar el código fuente de dicha técnica.
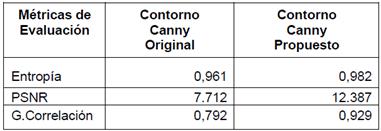
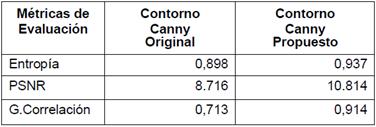
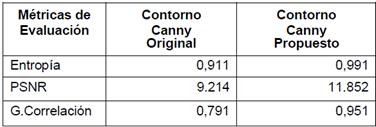
Las Tablas 1, 2 y 3 muestran la comparación de los resultados de las métricas obtenidas de la ejecución de los algoritmos, se observa que los valores obtenidos con la variante propuesta alcanzan una mejor precisión, correlación y entropía. Así también se puede observar que la adaptabilidad al ruido en las imágenes fusionadas (espectro visible con el infrarrojo cercano) ha mejorado considerando que se ha utilizado una categoría de imágenes que tienen alta variabilidad a condiciones extrínsecas.
Se analizan diferentes escenarios dentro de la categoría “Urban”: Edificios, Fachadas, Puertas, se selecciona esta categoría debido a que son las más afectadas por condiciones de variación de iluminación y texturas lo cual incide de manera directa en la variabilidad y complejidad de la detección de los contornos de las imágenes. Las tablas con los resultados, se muestran a continuación:
5. Conclusiones y Recomendaciones
Luego de analizar los resultados obtenidos en los experimentos realizados (ver Figura 4), y al visualizar las métricas obtenidas (Tablas 1, 2 y 3), se puede comprobar que la inclusión de la variante del filtro morfológico propuesto en (Deng, Wang, & Yang, 2013), reduciendo el tamaño del elemento estructurante, modificando la geometría del elemento e incluyendo una operación morfológica adicional de dilatación, mejora el filtrado del nivel de ruido. Por lo cual no se produce pérdida de los detalles de la imagen, ya que con esta variante, se logra adaptar de manera más precisa la detección de contornos en imágenes cross-espectrales. Esto permite extraer con mayor detalle los contornos, reduciendo la cantidad de falsos positivos en la detección de los bordes. Las métricas utilizadas reflejan una mayor entropía en la imagen y una mejor definición en la calidad de bordes detectados.
A partir de este trabajo, se pueden analizar las mejoras de otros algoritmos de detección de contornos como son Sobel, Prewitt, Robert, ZeroCross o Log para comprobar si se puede incluir filtros morfológicos para mejorar la precisión de detección ya sea para imágenes del espectro visible, infrarrojo cercano o Cross- espectrales. Se puede adicionalmente, definir nuevas métricas que sirvan para generalizar las mediciones de la precisión de las variantes propuestas, en varias técnicas de detección de contornos. También se puede analizar la variante propuesta en otros espectros como el infrarrojo lejano, etc.