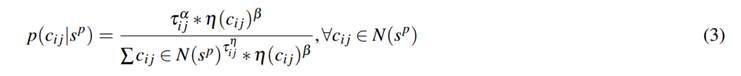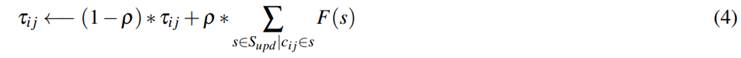INTRODUCCIÓN

Los algoritmos bio-inspirados surgen con la motivación de mejorar algoritmos de búsqueda para resolver problemas de optimización. Los algoritmos bio-inspirados son usados como metaheurísticas debido a que arrojan un conjunto de resultados a un problema en particular de manera total o aproximada al óptimo global. De acuerdo al fenómeno natural en que basan su diseño, se clasifican en dos grupos: Los Algoritmos Evolutivos (AEs) que emulan el proceso evolutivo de las especies (, ) y los Algoritmos de Inteligencia Colectiva (AICs) que emulan el comportamiento colaborativo de ciertas especies (algunas de ellas simples y otras inteligentes) como bacterias, abejas, hormigas, aves, peces, monos, entre otros (, ).

En las últimas cuatro décadas, el uso de metaheurísticas ha planteado ser una alternativa eficaz para resolver Problemas de Optimización Numérica con Restricciones (PONR). Aunque en un principio estos algoritmos fueron creados para resolver problemas de optimización sin restricciones, se han creado mecanismos adicionales para el manejo de restricciones tales como: función de penalización, decodificadores, operadores especiales, separación de la función objetivo y restricciones, reglas de factibilidad, entre otras (, ).

Un PONR también es conocido como el problema general de programación no-lineal y se puede definir como:

Donde 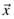∈ R ⁿ tal que n ≥ 1, es el vector de soluciones ⃗x = [x ₁, x ₂, . . . , x _n ] ^T , donde cada x _i , i = 1, . . . , n está delimitada por el límite inferior y superior L _i ≤ x _i ≤ U _i ; m es el número de restricciones de desigualdad y p es el número de restricciones de igualdad (en

ambos casos, las restricciones podrían ser lineales o no lineales). Si denotamos con F a la región factible (donde se encuentran todas

las soluciones que satisfacen al problema) y con S a todo el espacio de búsqueda, entonces debe ser claro que F ⊆ S ().

Los AEs son ampliamente utilizados como técnicas alternativas para resolver PONR. Los principales paradigmas son: los Algoritmos Genéticos (AG), la Programación Genética (PG), las Estrategias Evolutivas (EE), la Programación Evolutiva (PE), y la Evolución Diferencial(ED). Por otro lado, el AIC más popular es Optimización Mediante Cúmulos de Partículas (PSO, por sus siglas en inglés) (, ). Sin embargo, otras estrategias relativamente recientes han llamado la atención en el área por su utilidad para resolver con éxito problemas de optimización: Algoritmo de Optimización de Colonia de Hormigas (ACO, por las siglas en inglés de Ant Colony Optimization) (, ) y Colonia Artificial de Abejas (ABC, por las siglas en inglés de Artificial Bee Colony) (, ), ambos algoritmos principalmente se han utilizado para resolver problemas combinatorios (, ; , ; , ; , ).

ACO simula el comportamiento de las hormigas en busca de comida y su regreso al nido. Al inicio, la hormiga busca una fuente alimentaria. Si la encuentra, la hormiga deja un rastro de feromona a su regreso al nido, la cual atrae a las hormigas cercanas, de modo que sigan este rastro. Si más hormigas utilizan el mismo camino encontrado entre el nido y la fuente alimentaria, éste será escogido como el camino más corto por la alta concentración de feromonas.

En las últimas cuatro décadas, el uso de metaheurísticas ha planteado ser una alternativa eficaz para resolver Problemas de Optimización Numérica con Restricciones (PONR). Aunque en un principio, estos algoritmos fueron creados para resolver problemas de optimización sin restricciones, se han creado mecanismos adicionales para el manejo de restricciones tales como: función de penalización, decodificadores, operadores especiales, separación de la función objetivo y restricciones, reglas de factibilidad, entre otras (, ).

ABC simula el comportamiento de las abejas en la búsqueda de alimento. Biológicamente, las abejas realizan la búsqueda de fuentes de alimento a grandes distancias y al regresar a su panal revolotean haciendo danzas, las cuales transmiten la información de las fuentes de alimento localizadas. De manera artificial, el objetivo es el reclutamiento de abejas en una fuente de alimento y abandono de la misma (, ).

ACO y ABC son algoritmos cuyo potencial aún no es aprovechado a su máximo debido a su poca popularidad ( , ; , ; , ), aunque existen soluciones que han implementado estas metaheurísticas con éxito en problemas del mundo real (, ; , ). Por ello, esta investigación es motivada principalmente para explorar las capacidades de ambos algoritmos en la solución de un problema de optimización numérica conocido en el estado del arte como la minimización de una esfera.

Este problema es probado en 5 experimentos, donde se prueba el problema con dos y diez dimensiones, lo cual hace más complejo al problema. El objetivo principal de estos experimentos es detectar las características particulares y comunes que permiten un mejor rendimiento de estas dos metaheurísticas. Se busca analizar el beneficio de incrementar o decrementar las poblaciones de abejas y hormigas; así mismo de las iteraciones generacionales de estos algoritmos. Ambos algoritmos serán probados con los mismos parámetros para hacer una comparación justa al resolver el mismo problema de optimización.

El presente trabajo está organizado de la siguiente manera: En la Sección se describen brevemente los antecedentes de esta investigación dando una introducción a los algoritmos bio-inspirados, presentación del modelado del Problema de Optimización Numérica con Restricciones, y de los algoritmos a implementar en este trabajo: Optimización de Colonia de Hormigas y Colonia Artificial de Abejas. En la Sección , se describe brevemente al algoritmo de la Colonia Artificial de Abejas. De igual forma, el Algoritmo de Optimización de Colonia de Hormigas es descrito en la Sección . Los resultados de implementar ambos algoritmos en el problema de optimización de la esfera son presentados en el Sección . Finalmente, las conclusiones y trabajos futuros son presentados en la Sección .

Tabla 1 Parámetros del ABC 

Colonia Artificial de Abejas (ABC)

ABC se compone de 3 grupos de abejas que trabajan durante un máximo número de iteraciones MCN del algoritmo: abejas empleadas, abejas observadoras y abejas exploradoras. El número de abejas empleadas es usualmente igual al número de fuentes de alimento SN y se asigna una abeja empleada a cada una de las fuentes. Al llegar a dicha fuente, la abeja calculará una nueva solución (volará hacia otra fuente de alimento cercana) a partir de esta y conservará la mejor solución. El número de abejas observadoras es usualmente igual al número de abejas empleadas y son creadas aleatoriamente dentro del rango del espacio de búsqueda, sin embargo, se puede definir un parámetro para determinar el número de abejas observadoras. En este trabajo no se define otro parámetro. La función de la abeja observadora es visitar una fuente de alimento asignada con base en la aptitud de las abejas empleadas (valor de la función objetivo) y se calcula una nueva solución a partir de su fuente de alimento asignada y la información de la propia abeja observadora. Cuando una fuente de alimento no mejora después de un cierto número de iteraciones definido con el parámetro limit, ésta se abandona, siendo reemplazada por aquella encontrada por una abeja exploradora, la cual es una nueva abeja generada aleatoriamente ().

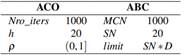
La ventaja de este algoritmo es el bajo número de parámetros que se requiere calibrar, como se puede observar en la Tabla .

La representación de las soluciones se lleva a cabo mediante fuentes de alimentos, los cuales son vectores de D-dimensiones (donde D es el número de variables de decisión del problema). La representación vectorial de la solución i en la iteración g es la presentada en la Ecuación ():

donde cada variable de decisión x _i está asociada a un rango L _i ≤ x _i ≤ U _i , el cual se debe tomar en cuenta para generar las fuentes de alimento iniciales de manera aleatoria con una distribución uniforme.

En el mecanismo de selección, la comunicación entre abejas empleadas y observadoras es indispensable, de manera que aquellas fuentes de comida con mejor calidad (mejor valor de aptitud) serán más visitadas. Las abejas son vistas como operadores de variación, cuando una de ellas llega a una fuente de alimento, se calcula una nueva solución candidata v _i,g utilizando la Ecuación ():

donde x _i,g representa la opción actual de la abeja, x _k,g es una fuente de alimento aleatoria y distinta de x _i,g , g es la iteración actual del algoritmo y φ es un número real aleatorio en el intervalo [-1,1].

El mecanismo para eliminar soluciones (fuentes de comida) es mediante las abejas exploradoras, es decir, cuando una solución no es mejorada (no es reemplazada por una candidata) durante el número de iteraciones establecidos por la variable limit donde su valor es

determinado por (SN ∗D). La fuente abandonada se reemplaza con una nueva solución generada aleatoriamente. Finalmente, la mejor solución encontrada durante la iteración se compara con la mejor solución en memoria y si tiene una mejor aptitud la reemplazará. El

pseudocódigo de ABC es presentado en el Algoritmo .

Colonia de Hormigas (ACO)

ACO se inspira en el comportamiento de búsqueda y provisión de alimentos de algunas especies de hormigas. Estas hormigas depositan feromona en el suelo con el fin de marcar algún camino favorable que debe ser seguido por otros miembros de la colonia. Los parámetros de ACO se presentan en la Tabla .

Como prerrequisito para aplicar un algoritmo ACO, se requiere de un “grafo de construcción”. La existencia de este grafo permitirá a las hormigas de la colonia recorrer dicho grafo para la construcción de las soluciones en forma cooperativa. Las hormigas artificiales construyen una solución para atravesar el grafo de construcción G _C (V , E). Este grafo totalmente conectado consiste de un conjunto de vértices V y un conjunto de arcos E. El conjunto de componentes C puede ser asociado con el conjunto de vértices V , o con el conjunto de arcos E. Las hormigas se mueven entre los vértices a lo largo de los arcos del grafo, construyendo incrementalmente una

solución parcial. Además, las hormigas depositan una cierta cantidad de feromona sobre los componentes, es decir, en los vértices

o en los arcos que atraviesan. La cantidad de feromona ∆τ depositada puede depender de la calidad de la solución encontrada. Las hormigas siguientes utilizan la información de la feromona como una guía hacia regiones más prometedoras del espacio de búsqueda. El pseudocódigo de ACO es presentado en el Algoritmo donde la aplicación del buscador local será decisión del usuario (La función AplicarBúsquedaLocal() es opcional).

En ACO una variable de decisión instanciada 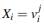(es decir, una variable Xi con un valor 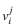asignado de su dominio Di, donde D

es el dominio de las variables 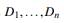y 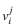es una distancia del grafo), se llama componente de una solución y se denota por c _ij . El conjunto de todos las posibles componentes de soluciones es denotado por C. Un parámetro de rastro de feromona T _{i j} es asociado con cada componente c _ij . El conjunto de todos los parámetros de rastros de feromona es denotado por T . El valor de un parámetro de rastro de feromona T _{i j} es denotado por τ _{i j} (y es llamado valor de feromona). Este valor de feromona es usado y actualizado por el algoritmo ACO durante la búsqueda, y permite modelar la distribución de probabilidad de diferentes componentes de una solución (, ).

ConstruirSolucionesporHormigas() Un conjunto de m hormigas artificiales construye soluciones a partir de elementos de un conjunto finito de componentes de soluciones disponibles C = c _{i j} , i = 1, . . . , n, j = 1, . . . , |D _i |. La construcción de una solución empieza con una solución parcial vacía s ^p = 0. Luego, en cada paso de la construcción, la solución parcial actual s ^p es extendida agregando una componente de solución factible del conjunto de vecinos factibles N(s ^p ) ⊆ C. El proceso de construcción de soluciones puede

ser considerado como un camino en el grafo de construcción G _C (V , E). Los caminos permitidos en G _C están definidos implícitamente

por el mecanismo de construcción de soluciones que define el conjunto N(s ^p ) con respecto a una solución parcial s ^p . La elección de una componente de solución de N(s ^p ) se hace probabilísticamente en cada paso de la construcción. Las reglas exactas para la elección probabilística de componentes de soluciones varían entre diferentes variantes de algoritmos ACO. La regla más conocida es de Ant

Tabla 2 Parámetros de ACO 

Tabla 3 Combinación de parámetros para la calibración de ACO y ABC 

System (, ) y se presenta en la Ecuación ().

donde τ _{i j} es el valor de feromona asociado con la componente c _{i j} , y η (.) es una función que asigna a cada paso de la construcción un valor heurístico para cada componente de solución factible c _{i j} ∈ N(s ^p ). Los valores que son retornados por esta función son llamados normalmente información heurística. Además, α y β son parámetros aleatorios positivos entre [0,1] cuyos valores determinan la

importancia relativa de la feromona y de la información heurística, respectivamente.

ActualizarFeromona() El objetivo de la actualización de feromona es incrementar los valores de feromona asociados con soluciones buenas o prometedoras, y reducir aquellos valores que están asociados con malas soluciones. Normalmente, esto se logra: 1) reduciendo todos los valores de feromona a través de la evaporación de feromona (evitar convergencia prematura del algoritmo) y 2) aumentando los niveles de feromona asociados con un conjunto de buenas soluciones S _upd como se calcula con la Ecuación ().

donde S _upd es el conjunto de soluciones que son usadas para la actualización, ρ ∈ (0, 1] es un parámetro llamado factor de evaporación, y F: S −→ R ⁺ es una función tal que f (s) < f (s ^′ ) ⇒ F (s) ≥ F (s ^′ ), ∀s ̸= s ^′ ∈ S. La función F ()˙ es llamada función fitness o de aptitud.

S _upd es un subconjunto de S _iter ∪ s _bs donde S _iter es el conjunto de soluciones que fueron construidas en la iteración actual, y s _bs es la mejor solución encontrada desde la primera iteración del algoritmo. Un ejemplo muy conocido es la regla de actualización de Ant System S _upd ← S _iter .

Pruebas y resultados

Los algoritmos ACO y ABC fueron implementados en el lenguaje M usando el software libre Octave 4.2.1, el cual es una variante libre de Matlab (, ). El problema de optimización (minimización) a resolver por ambos algoritmos es la bien conocida función de la esfera, la cual es definida en la Ecuación ().

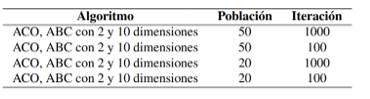
Se realizaron 5 experimentos para observar y analizar el comportamiento de los algoritmos ACO y ABC ante el problema de optimización numérica. Los primeros 4 experimentos consistieron en probar a ACO y ABC en el problema de la esfera con dos y 10 dimensiones empleando la configuración de parámetros mostrada en la Tabla en un total de 10 ejecuciones independientes por cada

algoritmo. El parámetro ρ fue un valor aleatorio entre (0,1] y limit fue SN ∗D para todos los experimentos.

Para el caso de dos dimensiones, la función de la esfera se representa como una curva en el plano. En el caso de tres dimensiones, se representa como una esfera propiamente dicha. Para el caso de cuatro o más dimensiones corresponde al hiperespacio.

Los resultados de la ejecución independiente de los algoritmos con cada una de las combinaciones se presentan en la Tabla de manera resumida, usando estadística básica como mejor y peor resultado, media, desviación estándar. Como se puede observar, en la mayoría de las ejecuciones el algoritmo ACO obtuvo mejores resultados con respecto a ABC y con una diferencia significativa según la prueba de Wilcoxon Signed Rank Test.

Para ambos algoritmos, resolver el problema de la esfera con diez dimensiones se vuelve más complejo que con sólo dos dimensiones. Por otra parte, se puede apreciar en la Tabla que no importa el número de población que tenga el algoritmo ACO: mientras más iteraciones haga, mejor será el resultado arrojado, puesto que se probó con población de 50 y 20 e iteraciones de 100 y 1000 obteniendo los mejores resultados con una población de 20 y 1000 iteraciones. Caso contrario ocurre con el algoritmo ABC, ya que a menor número de iteraciones se obtienen mejores resultados.

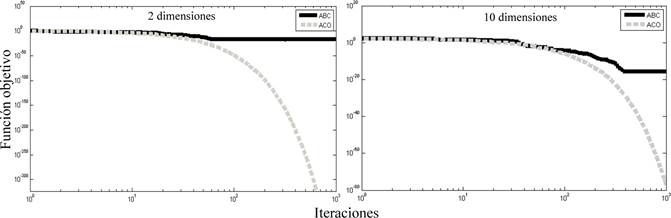
Figura 1 Gráfica de convergencia de ACO y ABC con 20 individuos y 1000 iteraciones en el problema de la esfera con 2 y 10 dimensiones 

En general, ACO obtiene mejores resultados al tener un mayor número de iteraciones y menor número de población. Es decir, entre menos hormigas y más tiempo, se acarrea más comida. En el caso de ABC, entre menos tiempo y más abejas, se recolecta más miel. Se puede apreciar que para ACO, la mejor combinación de parámetros es la de una población de 20 y 1000 iteraciones; para ABC la mejor combinación de parámetros es población de 50 y 100 iteraciones, tomando como referencia al problema con una dimensionalidad mayor, es decir, el problema de la esfera con diez dimensiones.

En el quinto y último experimento, ACO y ABC son ejecutados en el problema de la esfera con la mejor combinación de parámetros de los experimentos previos. Ambos algoritmos se ejecutaron de manera independiente 30 veces. Los parámetros utilizados en los algoritmos ABC y ACO son presentados en la Tabla . Cabe mencionar que se usó el mismo número de iteraciones y población para observar la convergencia de los algoritmos de manera equitativa.

Los resultados de la ejecución de ambos algoritmos en la función de la esfera con dos y diez dimensiones se presentan en la Tabla . Para el caso de dos dimensiones, se observa que los resultados estadísticos favorecen a ACO al encontrar el óptimo de la función en todas las ejecuciones tal como lo comprueba la desviación estándar de las 30 ejecuciones independientes. Sin embargo, ABC tiene resultados muy cercanos a la solución óptima del problema que en este caso es 0. Al realizar la prueba de Wilcoxon Signed Rank Test a los resultados de ambos algoritmos (mejor solución encontrada en cada una de las 30 ejecuciones independientes), se obtiene como resultado p-value = 0, por lo tanto, existe una diferencia significativa de los resultados entre ACO y ABC.

Para el caso de diez dimensiones, los resultados también favorecen estadísticamente al algoritmo ACO al obtener un mejor resultado

Tabla 4 Resultados obtenidos por los algoritmos ACO y ABC en las diez ejecuciones con distinta combinación de parámetros 

Tabla 5 Parámetros de ACO y ABC para la ejecución de las 30 ejecuciones independientes 

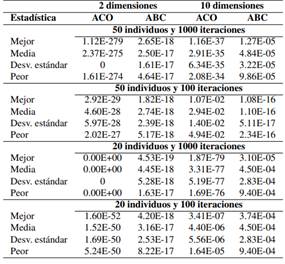
Tabla 6 Resultados estadísticos de ABC y ACO en el problema de la esfera con 2 y 10 dimensiones en 30 ejecuciones independientes 

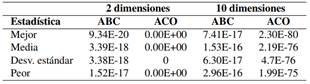
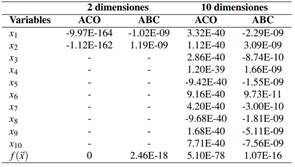
Tabla 7 Valores de ABC y ACO en el problema de la esfera con 2 y 10 dimensiones en la ejecución independiente 15 

que ABC y una desviación estándar mucho menor en comparación que ABC. Al realizar la prueba de Wilcoxon Signed Rank Test a los resultados de ambos algoritmos, la prueba da como resultado un p-value de 0 y un Z-value de -4.782. Por lo tanto, podemos concluir que existe una diferencia significativa de los resultados entre ACO y ABC.

La Figura presenta el comportamiento de ambos algoritmos en el problema de la esfera con dos y diez dimensiones en la ejecución número 15 de las 30 ejecuciones realizadas de manera independiente (mediana). Para el caso de dos y diez dimensiones, se puede observar que el algoritmo ACO tiene una convergencia hacia el óptimo después de pasar la mitad de las iteraciones. Por otro lado, ABC tiene una convergencia prematura en alguno de los óptimos locales del problema desde el principio de las generaciones. Sin duda, el algoritmo ABC tiene un verdadero problema de convergencia prematura.

Los valores finales de las variables y función objetivo de ambos algoritmos de las gráficas de convergencia se presentan en la Tabla .

De acuerdo con el análisis de complejidad de ACO (, ) y de ABC (, ), el coste computacional del primero es menor que el segundo, ya que el orden de complejidad de ABC es cuadrático. Comparando los resultados obtenidos por ACO y ABC con los obtenidos por otras metaheurísticas, por ejemplo el algoritmo de Cúmulo de Partículas (PSO, por las siglas en inglés de Particle Swarm Optimization), se tienen los siguientes resultados de un algoritmo de PSO modificado aplicado al problema de la esfera con diez dimensiones (, ): 1.11E-132 como mejor solución, 1.96E-121 como media, desviación estándar de

2.38E-122 y 6.44E-122 como peor solución.

De acuerdo con estos resultados, ACO y ABC se encuentran por detrás de PSO y otros algoritmos encontrados en el estado del arte. Sin embargo, si se aplica la prueba de Wilcoxon Signed Rank Test no hay diferencia significativa porque esta prueba considera irrelevantes valores con decimales muy cercanos a cero.

Conclusión

En este trabajo, se abordaron dos metaheurísticas de Inteligencia Colectiva (IC) para observar su comportamiento ante un problema de optimización conocido en el estado del arte como problema de la esfera y conocer los aspectos comunes y particulares que favorecen la convergencia prematura en el Algoritmo de Optimización de Colonia de hormigas (ACO) y Colonia Artificial de Abejas (ABC). Ambas metaheurísticas fueron programadas y adaptadas para resolver el problema de la esfera con dos y diez dimensiones usando el lenguaje de programación M empleando el software libre Octave 4.2.1. Un conjunto de experimentos fue realizado donde ambas metaheurísticas se ejecutaron con igual número de población e iteraciones para llevar a cabo una comparación justa usando medidas de rendimiento estadísticas y la prueba no paramétrica Wilcnxon Signed Rank Test, así como gráficos de convergencia.

Los primeros cuatro experimentos consistieron en probar a ACO y ABC en el problema de la esfera con dos y diez dimensiones con distinta población e iteraciones. Los mejores resultados obtenidos en estos experimentos fueron obtenidos con una población de 20 y 1000 iteraciones para ACO; para ABC la mejor combinación de parámetros es una población de 50 y 100 iteraciones, tomando como referencia al problema con una dimensionalidad mayor, es decir, el problema de la esfera con diez dimensiones. Un aspecto común encontrado fue que para ambas metaheurísticas resolver el problema de la esfera con diez dimensiones se vuelve más complejo que con sólo dos dimensiones.

Se observó que ACO obtiene mejores resultados cuando tiene un mayor número de iteraciones y menor número de población, es decir, entre menos hormigas y más tiempo, se acarrea más comida. En el caso de ABC, ocurre justo lo contrario: entre menos tiempo y más abejas, se recolecta más miel. Por lo tanto, una convergencia prematura ocurrirá a ambos algoritmos cuando la dimensionalidad aumente. Otro factor que provoca la convergencia prematura para el caso de ABC es una población pequeña de abejas sin importar si se tiene un gran número de iteraciones; en el caso de ACO una convergencia prematura puede ocurrir si se tiene un número menor de iteraciones sin importar el tamaño de la población.

Ambas metaheurísticas fueron probadas con el mismo número de población e iteraciones (20, 1000 respectivamente) en el problema de la esfera con dos y diez dimensiones, donde ACO obtuvo los mejores resultados y una convergencia estable hacia el óptimo global, caso contrario a ABC donde su convergencia fue prematura al caer en óptimos locales sin ninguna mejora al final de las iteraciones. Por último, la prueba de Wilcoxon Signed Rank Test arrojó una diferencia significativa entre los resultados de ACO y ABC.

Como trabajo futuro, ambas metaheurísticas deben ser probadas en más problemas de optimización numérica con restricciones, además de hacer experimentos donde otros parámetros de ambas metaheurísticas, aparte de la población e iteraciones, sean calibrados para conocer si estos parámetros también impactan en la convergencia y rendimiento de la metaheurística.