1. INTRODUCTION
Due to population and economic growth, road networks have been increasingly bearing higher loads of people and goods transportation. Globally, road network capacity is overloaded by congestion at the very time when it is needed most (during peak hours). Despite detrimental effects associated with congestion (pollution, casualties, capacity drop, spillback, gridlock formation, travel time variability; etc.), car ownership is steadily increasing every year (European Environment Agency, 2019). The traffic pressure faced by road networks on a daily basis is an important issue for road authorities, policy makers, and traffic engineers, who should provide solutions to eliminate congestion.
Since network expansion (building more infrastructure) is not always possible, a branch of research focuses on developing operational solutions that increase the performance of the system, which can be achieved by implementing dynamic traffic control measures. The main goal is maintaining efficiency and reliability of road networks within certain parameters, considering variations in traffic conditions. This can be achieved by several metering or buffering strategies (Papageorgiou et al., 1991; Lu et al., 2011; Butakov and Ioannou, 2015; Abadi et al., 2016; Zhang and Ioannou, 2016).
Ramp metering has been successfully applied in European countries such as the UK, Germany and the Netherlands, and has shown that proper control of on- ramps can improve traffic conditions in the mainstream and throughout the network (Caltrans District7, 2006; Horton et al., 2016); however, its application has been limited due to technical limitations and political concerns. Belgium offers an example where congestion levels increase every year, yet there is no active bottleneck management to control the increase of congestion on the network - 2017 was a record year with more than 1400 hours per day of travel time lost, due to more than 100 km of daily queues (VRTNWS: Laenen and De Roy, 2017).
In Latin America, literature is scarce on RM applications or comparison between RM strategies using a case study. Some applications were found in previous research (Günther et al., 2012; Noreña-Moreno, 2017; Cutipa and Lozano, 2020).
In Ecuador, Intelligent Transportation Systems (ITS) have been used to improve the safety of road users, especially those who use motorized vehicles on the roads. The ITS applications described in the literature focus on: information and communication technologies (ICTs) to aid routing decisions of heavy goods vehicles accessing the city of Quito (Zambrano et al., 2020 ); tracking public transport vehicles and transmitting their location and speed in real time to a control center (Calle Heredia et al., 2019); exploiting city-wide smartphone data as the main source of information to stabilize traffic in road networks (Zambrano et al, 2019). In Zambrano and Senti (2016), the authors describe ITS applications to control accident rates and improve safety in road transportation. The need to improve user information systems is obvious. However, there is a dearth of research and/or applications regarding the use of ITS for managing traffic flows on roads and highways.
The aim of this paper is to recommend the most adequate ramp metering strategy for a given situation, based on the case studies surveyed from the literature. Factors considered include road geometry, queue length, and the nature of the bottleneck. The benefits of a given strategy are shown in terms of gains (reduction of) in total travel time (TTS) spent in the network.
This paper is organized as follows: Section 2 discusses the basics of ramp metering strategies, classifies them, and concludes with a chronology. Section 3 reports findings from twenty-one ramp metering case studies, concluding with a graph showing reported gains in terms of TTS reduction. Concluding remarks are provided in Section 4.
2. RAMP METERING
Ramp Metering (RM) relies on a traffic light located at the on-ramp of a highway, which controls the inflow of vehicles onto the highway. Inflow is controlled by managing red and green phases of the traffic light through different strategies, such as fixed green times, one-car-per-green, two-cars-per-green, adaptive traffic conditions, etc.
When the demand at the on-ramp is greater than the allowed inflow of vehicles onto the highway, a queue forms at the on-ramp. The length of the queue must not be greater than the storage capacity of the on-ramp, otherwise queue spillback would disturb the surrounding network. When the metering rate is properly defined, the RM system ensures a reduction in the total travel time (travel time through and waiting time at on-ramps). Thus, the objective of RM is maintaining traffic flow on the highway under stable conditions, i.e., occupancy (ρ) below the critical value (ρcr) to avoid the occurrence of traffic breakdown.
RM can be used to maintain the capacity flow on the main stream and prevent blockages of upstream ramps, reducing the total time spent on the network by up to 50% (Papageorgiou and Kotsialos, 2002). In addition, RM can be used to enforce operationally desired traffic flow distribution, improve traffic safety and reduce emissions of pollutants to the environment (Ministerio de Transportes y Comunicaciones, 2018).
2.1 Ramp metering strategies
Technological advances, especially in ITS and ICTs, have allowed the development of RM strategies that increasingly consider more parameters for the dosage of traffic flow in the mainstream. RM strategies can be divided into fixed time, reactive, proactive and hierarchical structure or integrated highway network traffic control (Zhang et al., 2001; Papageorgiou and Kotsialos, 2002).
Fixed time strategies 2.1.1
They are used in offline applications. Their settings are based on historical data rather than real-time data.
Reactive strategies 2.1.2
These are based on real-time measurements collected by sensors installed on the highway network. They can be local or coordinated.
Examples of local reactive strategies are:
- Demand-Capacity. This strategy sets the ramp flow based on the difference between capacity downstream and upstream of the ramp, if the downstream occupancy of the highway is below the critical value; otherwise, a predetermined minimum ramp flow is used (Wattleworth, 1967).
- Occupancy-Capacity. If the mainstream occupancy (on the highway) at a point downstream of the merge area is below the critical occupancy, the metering rate is equal to the capacity minus the upstream demand; otherwise, a minimum metering rate is used (Wattleworth, 1967).
- ALINEA, is a feedback control strategy that uses real-time measurements of a given output to calculate appropriate values for input in real time, and then maintain output as close as possible to a given reference or target value. The objective of ALINEA is to keep traffic density on the highway equal to a given value
Where,
k = time interval.
r(k) = ramp metering rate.
KR = ramp metering gain.
ρ (k) = traffic density in interval k.
When traffic density on the highway becomes too high, the metering rate is reduced and vice versa. As Equation (1) shows, the control system responds to the changes in demand, but it does not anticipate them. This is an acknowledged limitation of ALINEA (Papageorgiou et al., 1991).
Coordinated reactive strategies are more efficient when there are multiple bottlenecks on the highway or when the storage capacity of the ramp is limited. These include multivariable control and optimal control strategies. Some examples are:
- ALINEA extensions, UP-ALINEA, PI-ALINEA, Queue control, Queue override, etc. (Papamichail et al., 2010).
- HERO (HEuristic Ramp metering coordination) is a reactive coordinated strategy for highways developed in 2006. It uses an extended version of the ALINEA feedback controller at the local level. HERO identifies active mainstream bottlenecks starting at a certain on-ramp, then creates a cluster with a master ramp and some slave ramps needed to meet the required storage capacity. This cluster is resolved when the occupancy of the master ramp is below a predetermined value (Papamichail et al., 2010).
- The Stratified Zone Algorithm consists of a three-layer hierarchical control structure: ramp, zone and system layer design. The strategy involves defining zone layers along the highway route from 0,5 km to approximately 5 km in length, calculating the metering rates for a confluence location according to the particular zone to which it belongs, and then selecting the most restrictive rate. This rate value is set as the rate for the location. In addition, the maximum allowed waiting times at on-ramps are set to a given value. The metering rule applied in this strategy is carried over to the ZONE metering concept, where the total inflow of vehicles onto a zone is balanced to the total outflow of vehicles from the section to avoid congestion (Zhang et al., 2001).
2.1.3 Proactive strategies
They are based on the prediction of traffic conditions within a determined period. These can be local or coordinated. Some examples are:
- Model Predictive Metering (MPC) is a proactive strategy that can be applied local or coordinated. It optimizes an objective function (such as TTS in the network) by using a highway traffic model to predict future behavior of the system for a given input sequence, by means of a receding horizon framework. Any parameter can be chosen for control and constraints can be considered as well. In a receding horizon framework, a prediction horizon is defined and metering rates are determined for each sample step by minimizing an objective function over that time period. Only the first calculated metering rate is applied to the ramp metering set-up, while the remaining are discarded and recalculated in a subsequent iteration (Bellemans et al., 2006).
- Nonlinear Optimal Metering can also be local or coordinated. It computes in real time an optimal and fair set of values for control, given current freeway and on-ramp traffic conditions, demand forecasts, on-ramp capacity storage, infrastructure capacity, current incidents, etc. AMOC was developed to implement this strategy (Mangeas et al., 2000).
AMOC is an Advanced Motorway Optimal Control tool that combines a second-order macroscopic traffic flow model to simulate the load on the network, with a coordinated ramp metering control strategy formulated as a dynamic optimal control problem with constrained control variables that is solved numerically for given demands and turning rates over a time horizon (Benmohamed and Meerkov, 1994).
- Sperry Algorithm is a coordinated proactive strategy that was introduced in Arlington (TX, USA). It is based on the demand-capacity strategy (Kotsialos et al., 2004).
- Linear programming algorithm is a coordinated proactive strategy that formulates the control problem as a linear optimization problem, where the objective function is the maximization of the weighted sum of ramp flows. The weight parameter indicates the importance of every ramp (Kotsialos et al., 2004).
- METALINE is a coordinated proactive strategy that manages control measures with the same goal as local strategies. As a generalization and extension of ALINEA, it uses all available mainstream measures to compute the ramp metering rate of all controllable on-ramps along the same route. Experimental results show that METALINE offers no advantage over ALINEA for recurrent congestion (urban freeways with a high density of on-ramps). However, for non-recurrent congestion (due to incidents), METALINE performs better than ALINEA (Papageorgiou and Kotsialos, 2002).
2.1.4 Hierarchical Structure or Integrated freeway network traffic control
These complex structures combine different metering strategies and exploit the synergistic effects that exist among them. It consists of three basic layers:
- The estimation/prediction layer, which uses historical and real time information from sensors installed on the freeway network. It provides the current state estimation and future predictions of the disturbances.
- The optimization layer, which uses the information from the previous layer as input to solve the optimal control problem, giving as a result the optimal on-ramp outflows and its corresponding optimal state trajectory.
- The direct control layer, which uses a pre-specified control algorithm to realize the suggested policy on a local level (Srivastava, 2011).
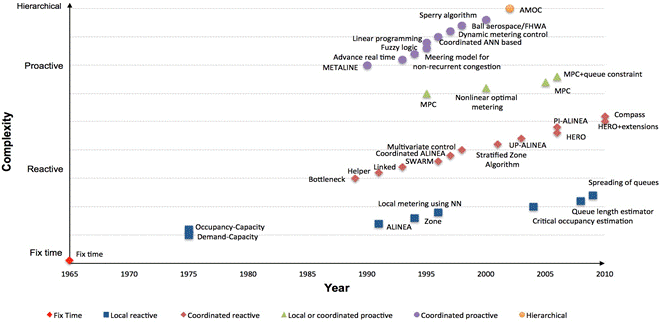
Figure 1 shows a chronology of the various ramp metering strategies that have been developed. They have been classified according to the year of publication (x-axis) and the complexity of the ramp metering strategy (y-axis). As Figure 1 shows, existing research responds to a learning process in the development of ramp metering strategies, starting with fixed time strategies that evolved into reactive strategies that showed some improvement in traffic conditions but had the disadvantage of becoming obsolete in a short period of time as traffic conditions changed. Then, the RM strategies evolved into proactive strategies which are able to anticipate the traffic changes through the control law due to their higher complexity and finally, the hierarchical structures take advantage of the progress of proactive strategies and also the synergy that can be achieved when different strategies are combined.
Moreover, there is a diversity of variants within the coordinated strategies (reactive or proactive), because there is evidence that local strategies are useful in cases where the traffic conditions of one ramp are independent of the traffic conditions of the other, but this is almost never the case in reality. Besides, the development of powerful computers has facilitated the development of algorithms for proactive strategies that are able to predict the occurrence of congestion and take measures to avoid it.
3. SELECTED LITERATURE
A total of 21 documents from articles, dissertations and manuals were analyzed, classified according to the ramp metering strategy analyzed and the year of publication. Since the goal of this work is to find out which ramp metering strategy achieves the highest gain in TTS in a given situation considering geometry, queue span, and type of bottleneck, almost all selected articles refer to at least two types of strategies that are compared in a case study. A brief description of each article is listed by RM strategy in a chronological order.
3.1 Fixed time strategies
In Papageorgiou et al. (1991), five different control strategies are compared with the no control scenario: static control (restriction in the flow entering from the ramp by physical elements), demand-capacity INRETS (demand-capacity strategy using measurements from three mainstream detectors), demand-capacity, percent-occupancy and fixed time strategy. Traffic data were collected on 13 days per strategy. The stretch consists of 1 km, which includes an on-ramp and an off-ramp on the inner side of the southern part of BP Périphérique in Paris. Although the divergent effect is mentioned, it was not considered in the evaluation of each strategy. The divergent effect refers to the re-routing that some drivers make to avoid congestion or the control system.
3.2 Reactive strategies
3.2.1 Local
Wu and McDonald (2003) present an experiment in the South East of England to determine the influence of ramp metering on driver behavior. This was done by switching off the operating ramp metering system (ALINEA) in the study area for four weeks in 2001 and then switching it back on for the same period. To quantify this impact, various indicators such as the difference in travel time, speed, headway, acceleration and deceleration, number of lane changes, speed distribution, headway distribution, traffic flow distribution, distance to merge, accepted gap size, accepted deceleration size, and merge speed were quantified. Data were obtained from instrumented vehicles (instruments provide quantitative information on driver behavior upstream and downstream of merging roadway segments), video cameras (11 cameras provide quantitative information on merging vehicles and interactions with the main traffic), and loop detectors (located upstream of merging segments, they provide speed and headway in the zone upstream of the merge). As expected, the only statistically significant difference found in the study is the number of lane changes (from the merging lane to the other) is when the ramp metering system is in operation.
Kerner (2006) introduces an approach to congestion control labelled ANCONA, which is based on the fundamentals of three-phase traffic flow theory (free flow, synchronized flow, and wide moving jam). Considering that the spillback effect of queues could block not only the upstream off-ramp but also the upstream on-ramp, ANCONA applies spatial confinement of congestion and uses the relatively high speed and larger discharge rate of synchronized flow to prevent the upstream propagation of congestion and reduce the waiting time at the traffic light in the on-ramp lane. Thus, the principle of ANCONA is to locate congestion arising at the bottleneck. The author tested the strategy on a two-lane highway section with a downstream bottleneck created by an off-ramp and an upstream bottleneck created by an on-ramp. The on-ramp and off-ramp merging sections are 0,5 and 0,6 km long, respectively. Traffic data were collected via two sets of detectors on the main highway control road.
Yasar et al. (2006) present the problem of the critical occupancy value, pointing out that if this value is lower than its actual value, the control law becomes overly conservative and leads to excessive waiting times at the on-ramps. On the other hand, if the value is set higher than the actual value, congestion on the freeway increases. To solve this problem, the authors developed C-MIXCROS and D-MIXCROS. These are two local feedback ramp metering strategies based on online estimates of critical occupancy. In the article, the authors use two methods proposed by Ozbay et al. (2006) for online critical density estimation using the Extended Kalman Filter and Kalman Filter techniques. These techniques take critical density as a state variable determined by downstream measurements of highway traffic. Through a simulation on an 11-mile corridor of the I- 295 highway in South Jersey, under various demand conditions, the authors show that MIXCROS strategies are very effective in reducing congestion on the isolated ramp system while keeping the on-ramp queue at an acceptable level.
Demiral and Celikoglu (2011) evaluate the performance of ALINEA at the approaches to the Bosphorus Strait bridges, for a time interval of one hour, and according to four demand patterns: constant, time-varying, sinusoidal, and real flow measurements. The findings supported decision-making regarding whether or not to build a third link between Europe and Turkey, due to excessive congestion on the existing O-1 and O-2 expressways. It was shown that the application of ramp metering enabled regulating the traffic pattern and maintaining traffic flow below the critical capacity of the existing road infrastructure. Moreover, after a brief description of various ramp management strategies, the authors argue for ramp metering as the best alternative. The study also reports some ramp metering algorithms as well as evaluation studies showing that the reduction of travel time in the mainstream can be counteracted by the increase of on-ramp delays by applying the algorithms HELPER, ZONE and BOTTLENECK within the microsimulation tool WATSIM. On the other hand, the evaluation of ALINEA, ZONE and BOTTLENECK with the PARAMICS microsimulation tool in this study yielded better results when the local occupancy control algorithm of ALINEA is replaced with the ZONE and BOTTLENECK algorithms. Further, ramp metering control is found to become less efficient during incidents. Finally, when evaluating METALINE, ALINEA and MIXCROS using micro and macro simulation tools, D-MIXCROS and C-MIXCROS performed better than the rest.
Wang et al. (2014) explore the ramp metering capability of the Proportional Integral ALINEA (PI-ALINEA) variant. This variant is designed for cases where ALINEA does not perform well, such as bottlenecks not being activated by the merging ramp due to lack of capacity far downstream of the metering point. In this particular case, occupancy should be measured downstream at the congestion point rather than in the merge area. To avoid this, and given the location of the actual bottleneck downstream, PI-ALINEA uses an extended structure that allows the downstream occupancy measured in the merge area to be used. It is shown in Equation (2):
Where k is the time interval, KP and KR are regulator parameters. The value of k should be larger than the free flow travel time between the merge area and the real bottleneck. To this end, three distinct bottlenecks were considered: an uphill road section (insufficient lane capacity causing a bottleneck), a lane drop (while capacity of the other lanes is held constant) and an uncontrolled on-ramp (uncontrolled entering flow activates a bottleneck). Bottlenecks take place on a freeway stretch (5,5 km) with 3 lanes; each bottleneck of 1 km starts 1,5 km downstream of the on-ramp. The upstream on-ramp is localized at 2 km from the start of the stretch. Simulations demonstrated that values of KR = 4 km.lane/h and KP = 100 km.lane/h in Equation (2) are universally applicable, and are not sensitive to the location of the downstream bottleneck.
3.2.2 Coordinated
Papamichail et al. (2010) demonstrate the advantages of HERO over other heuristics control strategies. Firstly, HERO allows taking coordinated actions even though the strategy is locally implemented. Therefore, HERO is a simple, generic and transparent algorithm. As HERO is feedback based, it is less perturbed by unexpected disturbances. The physical settings of HERO are as follows:
Mainstream and on-ramp data are processed in the Data Processing module, the outputs of which are inputs to the Queue estimation module, the Critical occupancy estimation module, the Queue override module, and the ALINEA core module, where flow at the ramp exit ramp is calculated. The output of the Queue estimation module becomes input to the Queue control and Minimum queue control modules. At the same time, outputs of these two modules, along with outputs of the ALINEA Core and Queue Override modules become inputs to the Final Ramp Flow Specification module, whose output is finally the input to the Implementation module. The Fail-Safe module makes decisions when the measurement system fails, and can enable/disable turns signal control based on preset traffic conditions on the main flow.
Yuan et al. (2009) conduct tests on HERO/RWS, a variant of the original HERO algorithm developed for and implemented at the Ramp Metering System in Netherlands, which seeks shifting congestion on motorways by an effective usage of upstream on-ramps storage space. HERO /RWS locally uses a variation of the demand-capacity algorithm, as it relies on highway flow and speed to calculate ramp flow. Model calibration is conducted based on three parameters (activation/deactivation parameters of HERO /RWS, critical speed, and flow of the freeway system), whereby robustness is tested by 12 simulation scenarios. Tests concluded that HERO /RWS cannot cope with traffic demand variations in congested networks, nor it is sensitive to speed changes or robust to flow variations. With respect to the ramp metering system, the authors conclude that upstream on-ramp coordination yields a less congestion, a higher mean speed, and lower travel time spent in the network. Hence, the authors note that coordination of the ramp metering system could be useful for closely spaced on-ramps with queues of unequal length. A stretch of the A10 ring road in Amsterdam was chosen for the simulation, which includes four consecutive on-ramps from the S105 to the Coen tunnel. The VISSIM micro simulator is used for model calibration and validation, by leveraging traffic data collected with double inductive loops during the evening peak period (15:30-18:00 h). Every on-ramp in the study is controlled by a ramp metering system. The bottleneck modelled took place downstream of the S101 on-ramp, reaching the S105 on-ramp upstream. This condition persisted throughout the whole simulation period.
Srivastava (2011) introduces the Stratified Zone Metering algorithm (SZM). The Minnesota Department of Transportation (MnDOT) uses this algorithm to control the level of congestion on highways, to study bottlenecks, and to understand the behavior of traffic breakdown and the response of traffic states to the metering patterns. The authors develop a methodology based on solving the differential equation in order to maintain traffic flow after intervening freeway mainlines. This analysis shows that the capacity of the bottleneck depends on the ratio between traffic flow at the mainline traffic and at the on-ramp bottleneck. Based on this finding, the author proposes a next generation Stratified Zone Metering algorithm (DSZM). This is a dynamic, zone-definition-based algorithm focusing on density rather than traffic flow, which allows overcoming the randomness of the current version by exploiting the stability of occupancy values near capacity. The study focuses on a 12-mile section of Trunk Highway 169 northbound (TH -169 NB), which traverses the western Twin Cities metropolitan region beginning at the I-494 interchange and ending at 63rd Avenue North. The section includes 10 weaving sections, 4 High Occupancy Vehicles (HOV) bypass ramps, 24 entrance ramps (17 metered), and 25 exit ramps. The roadway was modeled using the AIMSUM microsimulation tool, based on traffic data from the evening peak period.
Agarwal et al. (2015) propose a new method to perform coordinated ramp control. It is based on the relationship between freeway density just before the first merging, freeway density of the section between two consecutive ramps, and freeway density after the second merging. The method aims at keeping the aggregate traffic density on the freeway section equal to the critical density. The authors perform a ramp inflow rate control action upon occurrence of four different cases:
When upstream and downstream densities are lower than half of the critical density (
When upstream and downstream densities are higher than the critical density (
The upstream density is lower than the critical density and the downstream density is higher than the critical density (
The upstream density is higher than the critical density and the downstream density is lower than the critical density (
Ramp data at the intersection of I-15 NB and Tropicana and at the intersection of I-15 NB and Flamingo in Las Vegas were collected on a Thursday from 6 a.m. to noon. The on-ramps are controlled using data from the freeway sensors. The proposed control law allows a very close approximation to the target density, both at the freeway section between the two ramps, and after the second ramp as well.
3.2.3 Local and coordinated
Papageorgiou et al. (2007) highlight the importance of correctly estimating ALINEA parameters, pointing out that this strategy control variable consists of the on-ramp downstream occupancy (o out ), while a critical factor to consider is the location in which it is measured. Also, UP-ALINEA is presented as a solution to overcome the need for sensors downstream of the on-ramp to measure o out . UP-ALINEA is able to use measurements of upstream occupancy (o in ) to estimate the downstream occupancy (o out ) required to apply the control strategy. The approach is based on the following equation:
In Equation (3),
On the other hand, the authors warn about the inadequacy of microscopic models to simulate lane change behavior occurring in merged areas, which could lead to unexpected results.
Li and Ranjitkar (2013) rely on two performance indicators, total travel time and the Gini coefficient, to measure network efficiency and equity properties arising from the application of ramp metering and Variable Speed Limits (VSL). Considering that previous studies such as Zhang and Levinson (2004) and Shen and Zhang (2010) test the effect of control strategies on these properties without reaching consensus, the authors test ALINEA and HERO with the microsimulation tool AIMSUM to enhance previous results. The Gini coefficient is useful to analyze the degree of inequality in a given distribution. A value of 1 represents perfect equality, while 0 represents perfect inequality. This coefficient is calculated by the following expression:
Where G is the Gini coefficient,
The case study analyzed is a critical bottleneck section on State Highway 1 of the Auckland Motorway, connecting central Auckland to northern Auckland. This section has 5 on-ramps and 4 off-ramps towards Auckland city center. Traffic data is provided by the New Zealand Transport Agency (NZTA), including loop detector readings collected over 30-second periods at on-ramps, at off-ramps, and on the main road. Model calibration is conducted with the Geoffrey E. Havers (GEH) statistic based on data collected on Monday 12, March 2012, while model validation (also with GEH) is conducted with data collected on Friday 9, March 2012.
Donné (2015) studies buffering strategies to eliminate congestion on a ring road network through an application of optimal traffic management strategies that focus on avoiding Blocked Off-Ramps (BORs). Thus, ramp metering is applied to regulate the inflow that could trigger bottlenecks on the ring road. In addition, General Purpose Lanes (GPL) and Target Group Lanes (TGL - which allow free flow traffic) are utilized to improve traffic conditions for drivers that do not contribute to the creation of bottlenecks. The heavily congested Brussels Ring Road network is used to evaluate the proposed strategy, as a reasonable number of off-ramps are blocked on this ring road during peak hours. The inner and outer ring roads have a length of approximately 49 km, divided into individual links with an average length of 556 m. The length of the outer ring road is approximately 50 km. A total of 45 on-ramps and 46 off-ramps are directly connected to the inner and outer ring roads. Morning rush hour traffic data was used to test the control strategies.
Gains in total travel time spent on the network are determined from evaluation of 16 scenarios differing in the composition of the target groups, in the metering system, and with/without consideration of the capacity drop effect. When this effect is considered, 10% additional bottleneck capacity was considered for simplicity. Finally, the necessary infrastructure to establish the bypass for the TGL is outlined in general terms.
3.3 Proactive strategies
Papageorgiou and Kotsialos (2002) formulate in detail the problem of discrete-time optimal control (integrated in AMOC) considering ramp metering. This demonstrates the need for a proactive coordinated control strategy that utilizes all available storage capacity in the infrastructure (on-ramps and highways) to manage congestion in a more efficient and balanced manner.
The control strategy is tested by simulating the A10 ring road in Amsterdam. It consists of four main links and 2 tunnels. The simulation is conducted with traffic data from the evening peak, and only considers the counterclockwise direction of the A10, comprising 21 on-ramps and 20 off-ramps.
Papageorgiou et al. (2003) present some reasons for the theory-practice gap in the field of control networks. Among other, the authors highlight a bureaucratic and reactive administrative system which is iron-clad in doing things in conventional ways, conflicting interests between stakeholders, the complexity of advanced control systems, and the lack of knowledge of competent authorities. Moreover, the control loop problem is presented to explain how the efficiency of the network can be improved through an appropriate application of control strategies. From a practical standpoint, a field application for an on-ramp in the southern part of Boulevard Périphérique in Paris is used to show the advantages of ALINEA over demand-capacity control and occupancy- capacity control strategies. Finally, a simulation of the network-wide application of optimal ramp metering on the A10 ring road in Amsterdam is used to demonstrate the performance of the proactive coordinated control AMOC.
The European Ramp Metering Project, in its deliverable D2.2, gives an overview of the application and development of ramp metering systems in Europe until 2004 (Kotsialos et al., 2004). Eight applications are described: An isolated ramp in the middle of the A94 inner-city motorway ring in Munich; a virtual site on the A9 motorway north of Munich, where local traffic performance measurements from the on-ramp and mainline are used as input for control; the S101 on-ramp before the Coen tunnel to the A10-West motorway (part of the motorway ring around Amsterdam); a Delft-Zuid on-ramp onto the A13 highway towards Rotterdam, causing disruption to motorway traffic due to the merging process; the A28-De Uithof, A2-Maarssen Oost and A2-Breukelen West ramps in Utrecht; five main motorway sections in the southern part of the "Ile de France" in Paris; two J10 and J9 ramps on the M6 motorway in the UK; and a section on the Ayalon Highway (Telaviv-Israel) comprising 16 on-ramps and 17 off-ramps in both directions. These sites tested ALINEA, the adaptive fuzzy system for traffic responsive and coordinated ramp metering, demand- capacity and occupancy- capacity approaches.
Kotsialos and Papageorgiou (2004) test AMOC on the A10 ring road in Amsterdam (21 on-ramps and 20 off-ramps) to see if this ramp metering strategy provides efficient and fair control. AMOC achieves an optimal trade-off between reducing delay due to the reduction of the amount of congestion (main road), and increasing delay due to the metering system (on-ramps and off-ramps) that allows vehicles to exit before reaching the bottleneck. In addition, AMOC also achieves equity as it imposes maximum queuing constraints to distribute the delays experienced by drivers in the controlled on-ramps in a balanced manner. On the other hand, the experiment shows that not using the storage capacity provided by the freeways leads to severe underutilization of the freeway infrastructure during congestion.
Bellemans et al. (2006) use ALINEA and a controller based on MPC to define appropriate on-ramp metering rates. The authors simulate a 9 km stretch of the E17 motorway Ghent-Antwerp to test the control strategy. This stretch has 4 off-ramps, 5 on-ramps, and a tunnel underneath the river Scheldt. Traffic data corresponds to the morning peak hour. After the simulation, the authors show that metering rates, the evolution of average speed, and traffic density are much smoother with the MPC application. MPC takes the queue constraint as a hard constraint, meaning it is strictly respected in the optimization problem, whereas ALINEA resorts to a minimum imposed metering rate whenever the queue length threshold is exceeded. Moreover, the on-ramp coordination implied in ALINEA increases computational complexity without enhancing performance, since the optimization problem is solved at every iteration step.
Rinaldi et al. (2016) present an innovative method to solve the anticipatory network traffic control problem, introducing a dynamic clustering approach based on Principal Component Analysis that allows for problem decomposition. The approach focuses on the direct or indirect relationships that the control system can produce in the network. The anticipatory network traffic control problem is a powerful tool to reduce network traffic congestion, since it can account for road network user’s behavioral responses to determine the control strategy. Therefore, the method allows distinguishing control systems that can be successfully coordinated to maximize gains from a traffic condition point of view, from control systems in which coordination would only produce higher costs without relevant gains. Three simulations are conducted: a motorway stretch with two urban zones surrounding it; two parallel motorways running from North to South limiting an urban network with 20 uncontrolled intersections; and the same network with 4 controlled intersections and 16 uncontrolled intersections. The authors demonstrate superior performance of the method based on higher gains compared with other strategies such as local control ALINEA, fully centralized anticipatory control, and fully decomposed anticipatory control.
A second strategy modeled determines a single full network’s optimal control law which is solved only through an iterative coordination scheme, with the disadvantage that the number of iterations can grow indefinitely and it is very sensitive to the order in which the controllers are optimized due to a highly non-convexity solution space. Simulations are performed in online and offline applications.
3.4 Hierarchical structures
Kotsialos et al. (2005) highlight that a direct application of the AMOC solution may lead to different traffic states from the ones calculated by the optimal tool, due to errors associated with: the initial system state estimation, the prediction of future disturbances, model parameters used to determine the optimal solution, and unpredictable incidents in the network.
Moreover, it is demonstrated that a receding horizon approach allows accounting for traffic state variations, as it updates the control strategy at every iteration. In this case, a hierarchical structure uses AMOC in its optimization layer and ALINEA and flow-based ALINEA in its direct control layer. Additionally, a queue control policy is added to every local metering strategy. The applied horizon in the model predictive control is KA ≤ KP (update period ≤ optimization horizon), then the optimal control problem is solved again with updated state estimation and disturbance predictions, thereby closing the control loop of AMOC (feedback). Generally, this structure would yield more efficient control actions with increasing KP and decreasing KA. The authors simulate the A10 ring road in Amsterdam over a time horizon of 4 h (16:00 - 20:00h); the road has four main connections and 2 tunnels, 21 on-ramps, and 20 off-ramps.
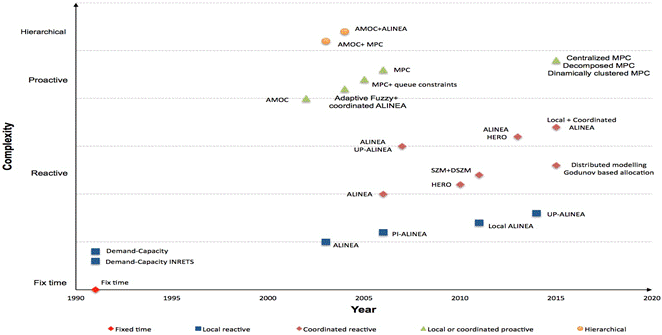
Figure 2 provides an overview of the literature reviewed. The horizontal axis shows the publication year and the vertical axis represents the complexity of the ramp metering strategy used.
As shown in Figure 2, literature that includes a case study (field application or simulation) is easier to find for reactive strategies (local or coordinated). The disadvantage of these strategies is that they cannot account for the response of traffic to the control system, therefore becoming inefficient in a short time. Of all the reactive strategies, ALINEA is the most popular, not only because of its algorithmic simplicity, but also because it performs very well compared to other strategies.
The development of powerful computer systems has facilitated the use of proactive strategies, which have the advantage of overcoming weaknesses of reactive strategies, and therefore promise greater benefits over a long period of time. However, these strategies require more and higher-quality data sources for collecting input data. The limitation of proactive strategies is that they do not exploit synergies among different control systems. Instead of proactive strategies, hierarchical structures can accommodate a mix of control strategies, strengthening their advantages and mitigating disadvantages as well. Deploying such structures requires more complex algorithms and systems for determining the input data required as well as for calculating and delivering the outputs sought.
It is important to note that coordination of upstream on-ramps should result in network benefits such as less congestion, higher average speed, and reduced travel time. In addition, not utilizing the storage capacity provided by freeway-to-freeway intersections could result in underutilization of freeway infrastructure during congestion, worsening traffic conditions in the system.
In addition to the type of strategy, improving traffic conditions through the use of ramp metering depends on correctly identifying the causes behind a bottleneck activation, as well as the location where congestion manifests. This information is also useful in determining the location where measurements should be taken for determining control parameters, such as occupancy upstream and downstream of the bottleneck.
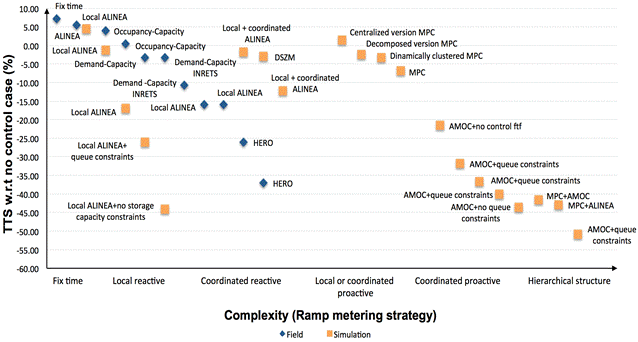
Figure 3 Ramp metering applications. Ramp metering strategies in the x-axis and reported gains expressed as the % TTS with respect to the no control scenarios in the y-axis (generated by the author)
Finally, it is important to be aware that relying on models to simulate the performance of ramp metering strategies could lead to incorrect results, as they are not able to adequately represent some effects that occur in reality, such as lane change behavior. Therefore, it is advisable to complement simulation results with real observations. Figure 3 shows the gains reported in the selected literature (in terms of reduction of total travel time on the network compared to the scenario without control). They have been classified according to the ramp metering strategy applied.
4. CONCLUSIONS
The application of ramp metering achieves relevant gains on heavily congested freeways with many ramps, where a trade-off between reducing the travel time of the main traffic and the waiting time on the on-ramps can be efficiently achieved. In this sense, considering queuing constraints helps to achieve a balanced distribution of queues in the system.
Local strategies are useful on ramps whose traffic flow is not affected by other ramps, either because the distance between them is very large or because it is not possible to use another ramp to reach the same origin-destination pair.
The analysis of the case studies revealed that proactive, coordinated and hierarchical structures are the most appropriate ramp metering strategies for highways where bottlenecks are caused by excessive demand, combined with geometric features such as different lane configurations and many ramps within the route - all these congestion-generating features normally result in long queues and block upstream ramps. The mentioned strategies incorporate a control law based on historical and real-time data, while also being able to anticipate traffic response, since the control law updates control parameters in each iteration. Moreover, they are able to predict the onset of congestion by anticipating queue formation and thus avoiding bottleneck activation. Further, these strategies allow consideration of additional constraints such as queue length or waiting time to limit the length of queues that could block upstream ramps. Finally, they are able to coordinate other ramps using all spare capacity (freeway-to-freeway intersections and urban on-ramps).
Developing algorithms to apply proactive coordinated and hierarchical structures in real time and in real networks is crucial, so it is essential that such algorithms are capable of achieving convergence within a few seconds.
Factors that deserve special attention when applying ramp metering strategies are quality of input data, the location where the data is collected, correct identification of bottlenecks, and the flow that contributes to the activation of the bottleneck.
The benefits of using ramp metering consist of an early identification of bottlenecks and the prevention or reduction of the capacity drop effect. Additional benefits come from the ability of ramp metering to decrease the spillback of queues, preventing blockage of upstream ramps. Other benefits include increased safety, efficient use of capacity, and increased network efficiency. Regarding the disadvantages of using RM, the authors highlight the spill back of queues onto the local road network, the need for enforcement, and the displacement of bottlenecks in the network.
Aspects that should be analyzed are the impact of the change in the split fraction between the main stream and off-ramp flow, on the allocated gains, as a consequence of the application of ramp metering; and the impact of ramp metering on travel behavior in terms of adjustment of departure times and driver awareness of changes in the traffic regime.