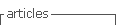1. INTRODUCCIÓN
El constante crecimiento poblacional y el incremento de las actividades económicas, aumentan la demanda de agua para: uso doméstico, agricultura, el sector industrial, la generación de energía eléctrica, recreación, entre otros. En este contexto, la construcción de presas para almacenamiento de agua permiten satisfacer dichas necesidades, constituyendo elementos indispensables para muchos países en vías de desarrollo (Altinbilek, 2002). De hecho, las presas han hecho aportes significativos para el crecimiento económico y social; así como también, han desempeñado un rol fundamental en la gestión del recurso hídrico, con miras a alcanzar la soberanía alimentaria y energética (Tortajada, 2015).
Actualmente, el embalse de Mulacorral tiene como objetivo la regulación y dotación de caudal destinado a riego y agua potable para la ciudad de Ambato, además de garantizar el caudal ecológico (Honorable Gobierno Provincial de Tungurahua, 2006 - HGPT).
Por otro lado, si bien es cierto, los beneficios que conlleva la construcción de una presa son numerosos, no se puede menospreciar que, la falla de una de estas estructuras ocasionaría daños en fauna, flora, infraestructura y pérdida de vidas humanas (Xiong, 2011). Específicamente, las inundaciones por rotura de presa han provocado desastres catastróficos para las vidas humanas, por lo que, los riesgos debido a esta causa, deben ser evaluados y mitigados cuidadosamente (Pen & Zhang, 2012).
Dentro de las causas de la falla de una presa se encuentran los factores hidrológicos, hidráulicos, geotécnicos, sísmicos, estructurales, operacionales y sabotaje (Yen y Tang, 1979). De los cuales, el factor hidrológico destaca debido a que el cambio climático global tiene incidencia directa sobre éste, pudiendo ocasionar que los diseños en etapas de factibilidad no se adapten a las condiciones de operación (Soares-Frazão et al., 2012).
Respecto a los factores hidráulicos y estructurales, el mayor porcentaje de fallas se producen en presas de materiales sueltos (tierra y enrocado) con alturas de entre 15 a 30 metros y con periodos de funcionamiento mayor a 5 años (Marengo, 1996); características presentes en la presa Mulacorral.
Con objeto de minimizar las posibles consecuencias de la falla de una presa, la modelación hidráulica del flujo post-rotura es un insumo importante para la creación de mecanismos de alerta temprana y evacuación de llanuras susceptibles a inundación (Begnudelli & Sanders, 2007; Xiong, 2011).
Para hacer frente a esta problemática, una de las opciones es el análisis mediante un modelo numérico computacional. La simulación numérica de inundaciones se desarrolla como un campo de investigación, debido al aumento de capacidades computacionales y a su disponibilidad (Prestininzi, 2008). En los últimos años, los ordenadores poseen un aumento exponencial en sus competencias sin incrementar su costo, haciendo que la modelación computacional sea una herramienta asequible y eficiente para simular el comportamiento de ríos durante avenidas (ShahiriParsa et al., 2016).
Dentro del amplio mercado de programas de modelación numérica, el programa HEC-RAS ha demostrado ser muy eficaz en la simulación de eventos de rotura de presas, proporcionando cálculos numéricos en una y dos dimensiones (Dasallas et al., 2019); así como también, en la capacidad de simular con precisión la propagación de inundaciones debido a este tipo de eventos, incluso en topografías empinadas y rugosas (Pilotti et al., 2020).
En el estudio, se consideró el planteamiento de escenarios hipotéticos, en los que se asume que el fallo de la presa no está asociado con algún evento sísmico o hidrológico, siendo el caudal disponible únicamente el almacenado en el embalse (4004630 millones de m3 - cota de embalse de 3836 m.s.n.m). Este volumen es obtenido a partir de la información del modelo digital del terreno, cuyo valor es mayor en 14.42% con respecto al proporcionado por el HGPT (2006); no obstante, un mayor volumen de agua representa un margen de seguridad.
Aunque se han alcanzado mejoras significativas en la modelación numérica de rotura de presa, es importante mencionar que, debido a las limitaciones del modelo numérico, las hipótesis de cálculo y la información cartográfica disponible; no se puede garantizar la precisión de los resultados, por lo que el presente análisis es de carácter referencial.
En consecuencia, la presente investigación se plantea los siguientes objetivos:
Determinar los calados (altura del nivel del agua) y velocidades máximas en las áreas probables de inundación producto del flujo post rotura de la presa.
Establecer el escenario de rotura de presa más probable, mediante la comparación con información de eventos históricos contenidos en la literatura.
Analizar el tránsito del hidrograma producido por la eventual falla de la presa, en puntos de control planteados desde el pie de la presa, hasta la periferia de la ciudad de Ambato.
2. CARACTERÍSTICAS DE LA PRESA MULACORRAL Y SU ZONA DE INFLUENCIA
La Presa Mulacorral está conformada por escollera (Figura 1), donde su cuerpo está compuesto por: un núcleo central, con material clasificado como grava limosa; filtros de grava arenosa, dispuestos en ambas caras de la presa; y espaldones compuestos por fragmentos rocosos, ubicados de menor a mayor granulometría, hacia los taludes de la presa. (Honorable Gobierno Provincial de Tungurahua, 2006).
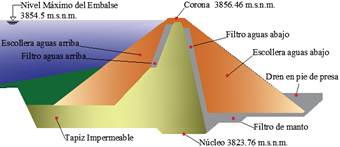
El embalse de Mulacorral tiene una capacidad máxima teórica de 3.5 millones de m3 en su cota de coronación, con un área inundada de 36 hectáreas. El embalse se abastece de las derivaciones de El Sombrero y El Tingo, y del agua proveniente de la subcuenca de la quebrada Mulacorral. El río de la Quebrada Mulacorral se une 7.1 kilómetros aguas abajo con el río Calamaca, que junto al río Colorado dan origen al río Ambato; como se muestra en la Figura 2.
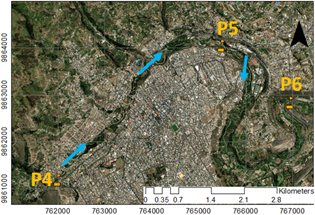
La zona de influencia corresponde a un área de 1585.49 hectáreas, con una extensión de 50.00 kilómetros, medida desde el pie de la presa hasta la periferia de la ciudad de Ambato. Se definió cinco puntos dentro de la zona de estudio: pie de la presa (P1), inicio del río Ambato (P2), sistema de captación Ambato-Huachi-Pelileo (P3), puente Jaramillo entrada de la ciudad de Ambato (P4), sector “El Socavón” (P5) y puente “Curvo” (P6); cuyas coordenadas y elevación se muestran en la Tabla 1.
Tabla 1 Coordenadas de puntos de control (WGS 84 - zona 17 S)
| Referencia | Código | Coordenada UTM | Elevación msnm | |
|---|---|---|---|---|
| X | Y | |||
| Pie de la Presa | P1 | 741801 E | 9867862 S | 3846 |
| Origen río Ambato | P2 | 742595 E | 9858298 S | 3266 |
| Captación A. H. P. | P3 | 749473 E | 9858527 S | 3004 |
| Pte. Jaramillo | P4 | 762004 E | 9861195 S | 2587 |
| Sector "Socavón" | P5 | 765493 E | 9864053 S | 2477 |
| Pte. "Curvo" | P6 | 766957 E | 9862840 S | 2401 |
En inspecciones realizadas en la zona de estudio, se constató: un total de 23 puentes, ubicados a lo largo del río Ambato; además de infraestructura localizada en los márgenes de una avenida hipotética, como: el Sistema de Captación Ambato-Huachi-Pelileo, la vía Flores (principal acceso a la presa Mulacorral y Chiquiurcu), la Planta de Tratamiento de Agua Potable de Tilulún, el parque Luis A. Martínez y la Planta de Tratamiento de Aguas Residuales.
3. SÍNTESIS DEL ESQUEMA NUMÉRICO UTILIZADO POR HEC-RAS
El uso de un programa de simulación numérica exige al usuario el entendimiento de los conceptos y algoritmos matemáticos, que el modelo emplea en la resolución de los problemas de ingeniería. HEC-RAS utiliza las ecuaciones de Saint Venant, las cuales son una derivación de la ecuación de Navier Stokes, y corresponden a un conjunto formado por las ecuaciones de Continuidad y Momentum (Hydrologic Engineering Center, 2016).
3.1. Ecuación de Continuidad
La ecuación de continuidad establece que, para diferentes secciones en un mismo canal, el caudal se mantiene constante en función del tiempo y del espacio; es decir, el caudal que entra a una sección de control debe ser igual al caudal que sale de dicha sección (Chow, 1994b).
Donde:
3.2. Ecuación de Momentum
Si se considera una presión hidrostática basándonos en: que la longitud horizontal es mucho mayor que la longitud vertical, la ausencia de cambios en la densidad y la ausencia de fuerza del viento; se puede llegar a la conclusión, que los términos de velocidad en el eje z pueden ser despreciados, obteniendo de esta manera las ecuaciones de cantidad de momentum (Chow, 1994).
Donde:
HEC-RAS utiliza dos esquemas para la resolución de las ecuaciones de Saint Venant, el primero ellos, “Full Momentum” resuelve las ecuaciones de cantidad de momentum sin omitir ningún término. El segundo, corresponde al Método de Onda Difusa o “Difussion Wave”, éste omite los términos de aceleración local y convectiva (Chow, 1994). En problemas relativamente simples, el modelo de onda difusa presenta tiempos de cómputo menores y resultados similares al método de Full Momentum. Sin embargo, en problemas que presenten cambios bruscos en la geometría, se recomienda de Full Momentum (Hydrologic Engineering Center, 2016).
4. METODOLOGÍA
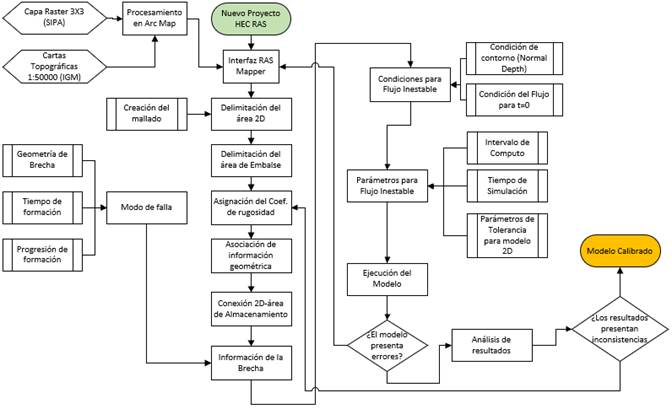
Sabat (2015) propuso un modelo y el diagrama de flujo para el análisis numérico del flujo inducido por el rompimiento de una presa, resolviendo las ecuaciones de Saint Venant 2D y considerando el método de volúmenes finitos. De manera similar, en este estudio se ha propuesto un diagrama de flujo (Figura 5), que contempla los pasos necesarios para modelar la inundación debido a la rotura de una presa en HEC-RAS 2D, el mismo que se fundamenta en los manuales presentados por el Hydrologic Engineering Center (2018).
4.1. Información Cartográfica
En el modelo, se consideró la siguiente información cartográfica:
Cartas topográficas a escala 1:50000, obtenidas de la base de datos del repositorio digital del Instituto Geográfico Militar (2012).
Modelos digitales del terreno (mdt), de precisión altimétrica igual a 1.5 m, con una definición de 3 por 3 m y 5 por 5 m, bajo el sistema de coordenadas WGS_1984_UTM_Zone_17S; obtenidos del repositorio digital del Ministerio de Agricultura y Ganadería (2019).
La capa se procesó mediante Sistemas de Información Geográfica (SIG), ArcMap, con el objeto de delimitar una posible zona de inundación. Es importante mencionar que, después de corridas preliminares en HEC-RAS 2D, la capa raster tuvo que ser corregida en el programa ArcMap, ya que existían zonas irreales de acumulación de agua.
En el modelo se estableció un mallado estructurado, correspondiente al área de influencia, el cual se encuentra conectado al área de almacenamiento (aguas arriba de la presa). Las características de la presa y el embalse utilizadas en la modelación se muestran en la Tabla 2.
4.2. Tipo de Flujo
Previo a la introducción de datos hidráulicos, es importante analizar las condiciones del flujo a simular con el fin de configurar de manera correcta el modelo. A continuación, un resumen del tipo y estado del flujo según Chow (1994a):
Tipo de flujo: el flujo producto de la rotura de una presa no presenta un caudal constante en función del tiempo y espacio, por lo cual, se ha clasificado como un flujo discontinuo rápidamente variado.
Régimen del flujo: esta clasificación es función de las fuerzas inerciales, de viscosidad y gravedad. En este caso, se puede presentar fluctuaciones entre el flujo subcrítico y el supercrítico, a lo largo del río.
Cabe mencionar que las modelaciones consideran únicamente las características (propiedades físicas) del fluido agua y no una mezcla agua-sedimento (fluido no newtoniano); es decir, no contempla cambios de la viscosidad dinámica y cinemática, condición que a priori, se traduce en un aumento en la incertidumbre de los resultados, principalmente en la zona aguas abajo de la presa.
4.3. Condiciones Inicial y de Contornos
Debido a la escala del evento a simular, se asume como condición inicial en la zona susceptible de inundación (aguas abajo de la presa), una la profundidad de agua igual a cero, es decir, una superficie de terreno seca.
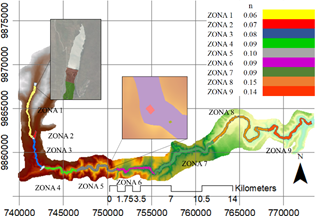
Se consideró como condición de contorno aguas abajo a la profundidad normal, mediante el ingreso de la pendiente del cauce de la sección final (Figura 3). Para ello, se utilizó el procedimiento para el cálculo de pendientes en ríos, empleado por Monsalve (1995). Es importante mencionar que, no se consideró a ríos aportantes los cuales presentan un caudal intrascendente en comparación al caudal producido post rotura.
Como condición aguas arriba, se definió el área del embalse, con un volumen correspondiente a la elevación máxima de agua en el embalse (cota de la corona). Es importante indicar que, la presa Mulacorral tiene un vertedero de excesos capaz de evacuar 23 m3/s y una tubería de toma que permite captar 4.14 m3/s en su máximo nivel de operación; no obstante, con el objetivo de presentar el caso más desfavorable, no se consideró estas descargas.
4.4. Coeficiente de Rugosidad
La calibración de un modelo numérico de inundaciones, fundamentalmente consiste en asignar un valor para el coeficiente de rugosidad (Ministerio de Medio Ambiente y Medio Rural y Marino, 2011). Esto se debe a que, el coeficiente de rugosidad influye directamente en los resultados de velocidad y profundidad de agua; por lo tanto, su determinación es de gran importancia en la configuración del modelo.
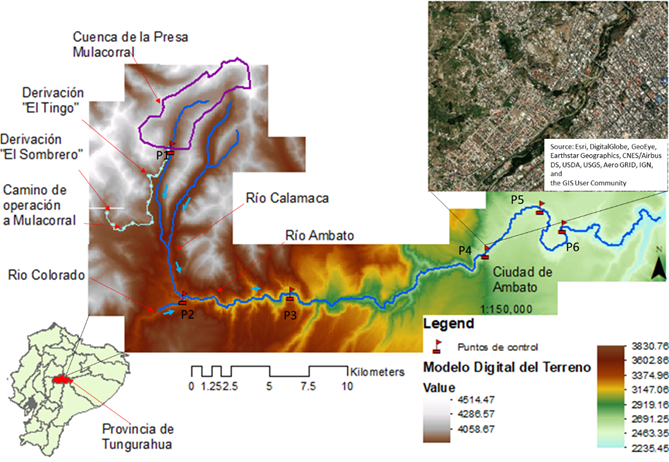
El proyecto de Mulacorral se diferencia de otros estudios como el de Pilotti et al. (2020) o Dasallas et al. (2019), debido a que carece de un evento histórico o modelo físico con el que se pueda comparar el coeficiente de rugosidad. Bajo esta condición, se tomó en cuenta la información de la literatura técnica, se definió el tamaño del mallado y se discretizó nueve zonas con diferentes valores de rugosidad.
Se utilizó la ecuación de Cowan para definir el valor del coeficiente de rugosidad “n” de Manning, la cual, utiliza variables respecto a: el material del canal, grado de irregularidad, variaciones en la sección transversal, efecto de obstrucciones, vegetación y efectos de meandros (Cowan 1956, Chow 1994a).
Adicional, siguiendo las recomendaciones del Hydrologic Engineering Center (2014), se consideró establecer un coeficiente de rugosidad que simule la turbulencia en la zona inmediatamente aguas abajo de la presa; además, se asignó un coeficiente que considere la infraestructura en las orillas del río Ambato y en la zona de probable inundación, como lo establece el Engineers Australia (2012). En la Figura 4, se muestran las nueve zonas definidas con su respectiva rugosidad.
4.5. Generación de la Brecha
Los parámetros que inciden en el cálculo del hidrograma de salida de la presa, dependen de: su modo de falla, características de la brecha y tiempo de formación (Hydrologic Engineering Center, 1980). En afán de abarcar el mayor número de escenarios, se trabajó con las ecuaciones: Guía Técnica-1996 (Ministerio de Medio Ambiente, 2001); Froehlich (2008), MacDonald & Langridge-Monopolis (1984), Von-Thun & Gillette (1990) y Xu & Zhang (2009). Las cuatro últimas están incorporadas en el programa HEC-RAS 5.0.7 (Hydrologic Engineering Center, 2016).
A continuación, se exponen las consideraciones tomadas para el ingreso de datos referente a la formación de la brecha:
Para el caso de una presa de materiales sueltos el tiempo de formación de la brecha es progresivo.
El centro y elevación del fondo de la brecha son consideraciones específicas, que dependen del modelador y de las características de la presa. Para este caso se ha considerado que el centro de la brecha se encuentre en el eje de la presa y que el fondo de la brecha corresponde al nivel más bajo del mdt.
Los valores obtenidos mediante las ecuaciones descritas, se indican en la Tabla 3.
Tabla 3 Tiempo de formación y geometría de la brecha; a) presa con alta erosionabilidad, b) presa con baja erosionabilidad
| Ecuación | Ancho (m) | Tiempo de formación (horas) | Pendiente de taludes |
|---|---|---|---|
| Guía Técnica | 38.96 | 0.42 | 1H:1V |
| Froehlich (2008) desborde | 30.00 | 0.51 | 1H:1V |
| Froehlich (2008) tubificación | 24.00 | 0.50 | 0.7H:1V |
| MacDonald & Langridge-Monopolis (1984) | 10.00 | 0.66 | 0.5H:1V |
| Von Thun & Gillette (1990) a | 62.00 | 0.33 | 0.5H:1V |
| Xu & Zhang (2009) a | 54.00 | 0.55 | 2.01H:1V |
| Von Thun & Gillette (1990) b | 62.00 | 0.50 | 0.69H:1V |
| Xu & Zhang (2009) b | 29.00 | 3.26 | 0.96H:1V |
4.6. Análisis de Sensibilidad
4.6.1. Balance del Volumen de Agua
Como lo establece Wang (2020), un análisis de equilibrio del volumen del agua es fundamental para establecer la coherencia de un modelo numérico. Para definir el mdt que utilizó este análisis, se modeló y calculó el volumen acumulado con el mdt de 3 por 3 m y con el de 5 por 5 m, en iguales condiciones y tolerancias del programa. En la Tabla 4, se muestran los resultados del volumen acumulado, para los puntos de control P1, P2, P3 y P4.
Tabla 4 Balance de agua para los mdt de 3 por 3 m y 5 por 5 m
| mdt 3x3 | mdt 5x5 | ||||
| Volumen acumulado m3 | Error relativo % | Volumen acumulado m3 | Error relativo % | ||
| P1 | 4004377 | 0.01 | 3993793 | 0.27 | |
| P2 | 3988199 | 0.41 | 3522588 | 12.04 | |
| P3 | 3929828 | 1.87 | 3483256 | 13.02 | |
| P4 | 3759947 | 6.11 | 1778944 | 55.58 | |
En el modelo con el mdt de 3 por 3 m, se puede observar que el error en el balance del volumen de agua en el punto P4 es del 6.11%, por otra parte, el de 5 por 5 m mostró un desfase de más del 55%, lo cual se atribuye a la baja definición del mdt en las riberas del río Ambato, produciendo acumulación de agua.
4.6.2. Tamaño de Celda
Como lo establece el Hydrologic Engineering Center (2018), HEC-RAS permite obtener resultados similares con diferentes tamaños de celda en el mallado. En este sentido, con el objeto de establecer la relación adecuada entre tamaño de celda y tiempo de cómputo, se realizaron simulaciones con el mdt de 3 por 3 m, para un mallado de 6 por 6 m y 12 por 12 m de tamaño de celda. En la Tabla 5, se muestran para los puntos P1, P3 y P4, los resultados de calados, velocidad y caudal pico en función del tiempo.
Se puede observar que los valores de velocidad y calado son similares, con base en esto y al tiempo de cómputo, 4 veces menor, se determinó que la malla con celdas de 12 por 12 m presenta mejor relación entre tamaño de celda y tiempo de procesamiento. De igual manera, se puede verificar que los caudales pico presentan la misma evolución a través del río.
Tabla 5 Comparación de mallas (tamaño de celda) en función de la velocidad, calado, caudal y tiempo de cómputo
| Celda 6x6 tiempo computo: 4horas:10 min | Celda 12x12 tiempo computo: 1hora:10min | |||||
|---|---|---|---|---|---|---|
| Velocidad m/s | Calado m | Caudal Pico m3/s | Velocidad m/s | Calado m | Caudal Pico m3/s | |
| P1 | 7.95 | 8.59 | 4609 | 6.33 | 8.74 | 4615 |
| P3 | 7.15 | 11.45 | 2292 | 6.94 | 11.28 | 2371 |
| P4 | 3.51 | 6.97 | 1057 | 3.73 | 7.15 | 1307 |
Los análisis de sensibilidad fueron desarrollados en un ordenador con las características que se detallan en la Tabla 6.
Tabla 6 Características del computador utilizado en la modelación
| Modelo | Intel® core™ i7-8700 CPU @3.2GHz 3.19 Hhz |
| Núcleos | 6.00 |
| RAM | 16.00 GB |
| Sistema Operativo | Windows 10 |
| Procesador | 64.00 bits |
Como lo establece el Hydrologic Engineering Center (2016), la base fundamental para obtener un modelo hidráulico confiable es la calidad y confiabilidad de información topográfica a utilizar. El hecho de realizar un mallado fino en un mdt de baja calidad, será contraproducente para el estudio, por este motivo, el modelo bidimensional se trabajó en función del mdt de 3 por 3 m y con un mallado de 12 por 12 m.
La Figura 5 presenta el diagrama de flujo que sintetiza el desarrollo de la metodología planteada en este análisis.
5. MODELACIÓN DE ESCENARIOS
Se plantearon diez escenarios para analizar el caudal pico en distintos puntos de control. Posteriormente, se obtuvo el error absoluto para determinar los escenarios más y menos desfavorables; los casos tomaron en cuenta los siguientes parámetros:
Modo de falla
Ecuación de resolución del modelo numérico
Ecuación de regresión para formación de brecha
5.1. Modo de falla - Desborde y Tubificación
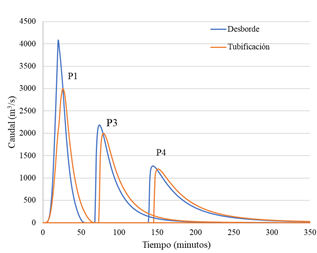
Se planteó la utilización de la ecuación de Froehlich-2008 (Hydrologic Engineering Center, 2016) para definir la formación de la brecha por tubificación y desborde. Se utilizó la ecuación descrita por Froehlich ya que como cita Rodríguez et al. (2015), ésta ecuación representa de mejor manera la formación de brechas en presas zonificadas. La Figura 6, muestra que el caudal pico en P1 presentó una diferencia de 1073 m3/s, comparando el modo de falla de desborde con el de tubificación, esta diferencia disminuye conforme avanza la avenida hasta P4, donde la diferencia es del 5.48% y con un desfase de llegada de 7 minutos.
Es importante indicar que la distribución de los hidrogramas para ambos modelos, cumple con el balance de volumen de agua.
5.2. Resolución del modelo numérico
Los modelos numéricos que maneja HEC-RAS son el método de “Full Momentum” y “Diffusion Wave” (Hydrologic Engineering Center, 2018). Se puede apreciar en la Figura 7 que, para P1 ambos modelos presentan hidrogramas que se superponen. Sin embargo, en el punto de control P2 el modelo de “Diffusion Wave” presenta inestabilidad. Esto concuerda con lo mencionado por el Hydrologic Engineering Center (2016), la resolución por el método de “Full Momentum” alcanza una mayor precisión y estabilidad en problemas de mayor complejidad. Cabe indicar que ambos modelos compartieron las mismas condiciones de borde y mdt, por lo cual se descarta una falla de modelo de Diffusion Wave por estas condiciones.
5.3. Ecuación de Regresión
Para la indagación de los efectos debido a la ecuación de regresión para formación de brecha, se realizó una sub clasificación entorno a efectos de erosión en el cuerpo de la presa. La Figura 8 muestra los hidrogramas para diferentes ecuaciones de geometría y tiempo de formación de la brecha, en función del volumen de almacenamiento y dimensiones geométricas de la presa y sin contar con factores de erosión.
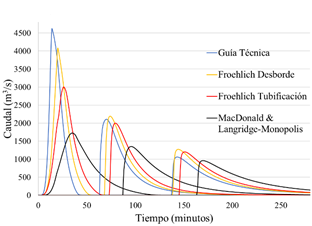
Figura 8 Hidrogramas en los puntos de control P1, P2, P3 y P4, utilizando ecuaciones con base en la geometría y el volumen de almacenamiento
En la Figura 8, se puede observar un caudal pico máximo de 4616.53 m3/s para la ecuación de la Guía Técnica y un caudal pico mínimo de 1723.91 m3/s correspondiente a la ecuación de MacDonald & Langridge-Monopolis (1984). Sin embargo, para P4 las ecuaciones presentan una diferencia de picos de caudal entre 1264 y 959 m3/s y un desfase de 24 minutos.
Por otro lado, la Figura 9 servirá para establecer las diferencias entre una presa construida técnicamente (menor erosión) y una presa construida sin fundamento ingenieril o formada de forma natural (mayor erosión). Estas ecuaciones consideran efectos de erosión, características geométricas y volumen de almacenamiento. Esta figura muestra una evolución gradual de manera similar, sin embargo, la ecuación de Xu & Zhang (2009) para una presa con poca erosión, presenta un tiempo extendido en la formación de la brecha.
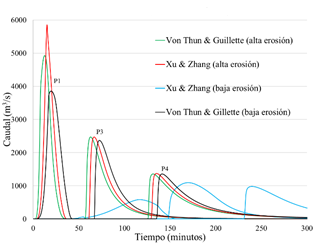
Figura 9 Hidrogramas en los puntos de control P1, P2, P3 y P4 utilizando ecuaciones con base en efectos de erosión
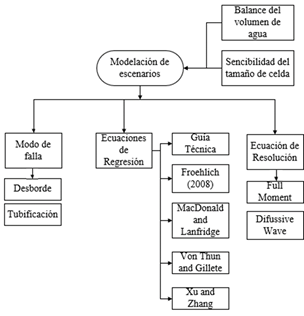
En la Figura 10, se plantea el proceso entorno a la modelación de los distintos escenarios de rotura para la presa Mulacorral.
6. RESULTADOS Y DISCUSIÓN
6.1. Caudales Pico
La Tabla 7 resume los caudales pico obtenidos de los planes de modelación en el punto de control P1 (pie de la presa). En la misma, se calculó el error absoluto para establecer un intervalo de resultados. En base al error absoluto y asumiendo como correcto al valor de caudal pico promedio, se podría expresar nuestro margen de error es 3577.47 ± 613.83 m3/s; con base en este criterio los caudales pico que representan al modelo son los obtenidos mediante las ecuaciones de Froehlich (2008) y Von-Thun & Gillette (1990) b.
Tabla 7 Caudales pico para los escenarios de rotura de la presa Mulacorral en el punto P1
| n | Ecuación | Caudal Pico (m3/s) | x-xm | (x-xm) ^2 |
|---|---|---|---|---|
| 1 | Guía Técnica | 4616.5 | 1039.1 | 1079644.1 |
| 2 | Froehlich (2008) desborde | 4073.4 | 496.0 | 245994.4 |
| 3 | Froehlich (2008) tubificación | 2999.7 | -577.8 | 333838.3 |
| 4 | MacDonald & Langridge-Monopolis (1984) | 1723.9 | -1853.6 | 3435675.6 |
| 5 | Von Thun & Gillette (1990) | 4914.6 | 1337.1 | 1787952.1 |
| 6 | Xu & Zhang (2009) | 5851.4 | 2273.9 | 5170678.3 |
| 7 | Von Thun & Gillette (1990) b | 3857.3 | 279.9 | 78328.1 |
| 8 | Xu & Zhang (2009) b | 582.9 | -2994.6 | 8967748.0 |
| xm= | 3577.47 | ∑= | 21099858.96 |
Considerando que los hidrogramas de ambas ecuaciones convergen en el punto de control P4 y con base en el criterio del Bureau of Reclamation (1998) de adoptar el escenario más desfavorable, se presenta el modelo de Froehlich por desborde, ya que muestra magnitudes mayores y representaría resultados más conservadores.
La Figura 11 presenta la relación entre caudales picos observados y calculados por la ecuación de Froehlich (rojo) obtenidos del registro del Bureau of Reclamation (1998). En esta gráfica se ha incorporado los caudales pico obtenidos en la modelación y calculados con la ecuación mencionada (color azul). A pesar de que, el modelo de tubificación se encuentra más cerca de la línea de tendencia, se escoge el escenario por desborde por el fundamento planteado anteriormente.
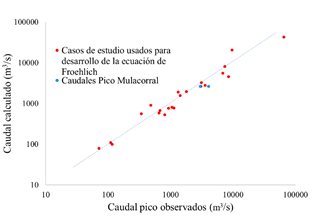
Figura 11 Caudales pico observados y calculados usando la ecuación de Froehlich (1995), extraída de Dam Safety Office (1998); y caudales pico Mulacorral
6.2. Velocidades y Calados
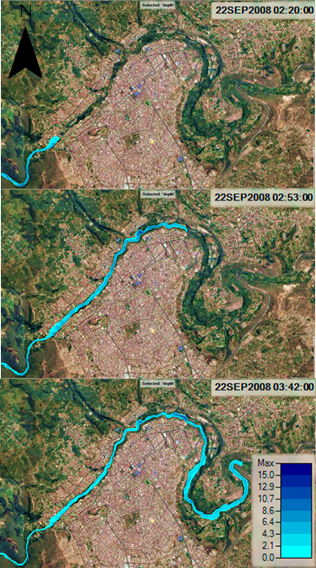
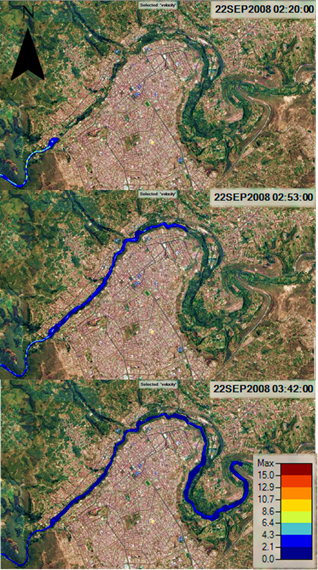
Se estima que la avenida ingresa a la ciudad en el sector del Puente Jaramillo (P4) a las 2 horas con 20 minutos con un calado de 6.67 metros y una velocidad de 3.35 m/s. A las 2 horas con 53 minutos, la onda llega al sector de “El Socavón” (P5), con un calado 5.31 metros y una velocidad de 2.72 m/s. A las 3 horas y 42 minutos de iniciarse la falla de la presa, el flujo llega a la periferia de Ambato, al pte. “Curvo” (P6), donde se presenta una altura de agua de 4.16 metros y una velocidad de 2.55 m/s.
En la Figura 12, se observa el paso del flujo post rotura por la ciudad de Ambato, apreciándose que debido a la lejanía de la presa Mulacorral, el centro con más densidad poblacional no es afectado. Sin embargo, las riberas del río y la infraestructura que se encuentra dentro de sus márgenes, presenta calados entre 7 y 5 metros de altura.
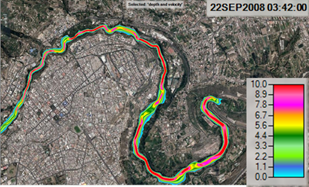
De forma simultánea, la Figura 13 presenta los resultados de velocidades para cada punto de control ubicados en la ciudad de Ambato, los cuales están en un rango de 2 a 3 m/s.
El resumen de los valores máximos para calado y velocidad se muestra en la Tabla 8.
Tabla 8 Cuadro de velocidades y calados máximos para el modo de falla por desborde de la presa Mulacorral
| Velocidad máx. | Calado máx. | |
| Control | m/s | m |
| P1 | 5.90 | 8.29 |
| P2 | 11.32 | 11.00 |
| P3 | 6.83 | 10.76 |
| P4 | 3.73 | 7.08 |
| P5 | 3.12 | 5.55 |
| P6 | 2.02 | 5.86 |
6.3. Hidrogramas de llegada a la ciudad de Ambato
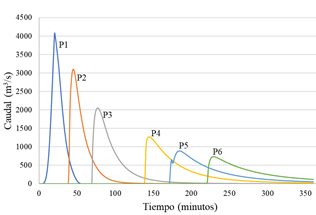
La Figura 14 muestra la atenuación de la onda de crecida, desde el pie de la presa (P1) hasta el puente “Curvo” (P6). Se presentan valores de 1271 m3/s en el puente Jaramillo, hasta 731 m3/s en el puente “Curvo”, a 47 kilómetros de distancia de la presa.
Considerando una relación simple entre longitud y tiempo que en llegar hasta la ciudad de Ambato, se puede obtener un valor de la velocidad con la que viaja la onda de 12 km/h.
6.4. Área potencialmente afectada
Se debe tener en consideración que valores de calado mayor a 1 metro de altura y velocidad mayor a 1 m/s representan riesgo potencial a vidas humanas, daños en infraestructura y ambiente (Ministerio de Medio Ambiente y Medio Rural y Marino, 2011). HEC-RAS permite obtener esta razón de velocidad y calado misma que se muestra en la Figura 15.
El estudio refleja un área de inundación correspondiente a 566 hectáreas, repartidas en las riberas del río Ambato, con un alcance aproximado de 50 metros a ambos lados del eje del río. No obstante, este dependerá de la morfología del río y los taludes de la zona.
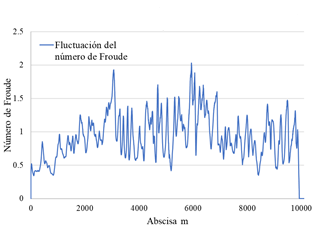
La Figura 16 muestra la variación del régimen de flujo entre el punto de control P1 y P2, a 36 minutos de haberse iniciado el proceso de falla de la presa. Se verifica de acuerdo a la literatura que, conforme transita el frente de onda, el régimen de flujo pasa de un estado supercrítico a un estado subcrítico (Toro, 2001; Prestininzi, 2008).
Para finalizar, las Figuras 17 y 18, presentan la ubicación de los puntos de control y la visualización en tres dimensiones, utilizando la herramienta de 3D View incorporada en versión 5.0.7 de HEC-RAS.
7. CONCLUSIONES
Los rangos de velocidad, niveles de agua y caudales pico obtenidos mediante HEC-RAS, fueron comparados con fórmulas empíricas que se fundamentan en información de eventos históricos. Por lo tanto, este estudio se concibe como un análisis que muestra resultados referenciales, más no con fines de diseño o construcción de infraestructura.
La evolución de los hidrogramas mostró que las condiciones iniciales de formación de la brecha, tienen poca influencia en lugares que se encuentran alejados del evento de falla.
Los resultados de caudal pico obtenidos concuerdan con lo dicho por Wahl (2014), donde se establece estadísticamente que las ecuaciones de Froehlich (2008), Von-Thun & Gillette (1990), son mejores para predecir el tiempo de formación de la brecha. Por otra parte, la ecuación de Xu y Zhang (2009) presenta tiempos significativamente más largos, en este caso el tiempo de llegada de la onda a la ciudad de Ambato, con un desfase de 4 horas en relación a los otros modelos.
Un mallado bidimensional en una zona con pendientes encañonadas, como se dio en este caso, demandará de más gastos computacionales, los cuales pueden ser optimizados realizando una sección de una dimensión, siempre y cuando se haya comprobado que los modelos bidimensionales y unidimensionales presenten resultados relativamente iguales.
Se contempla una afectación directa el 65 % de la Vía Flores, debido al calado y la velocidad alcanzados en las riberas del río. Esto aumentará el tiempo de respuesta de acciones de ayuda en los poblados afectados en la zona media y alta del río Ambato en el hipotético caso de la rotura de la presa Mulacorral.
En caso de tener una zona extensa de estudio, donde se encuentren diferentes tipos de sustratos y características geométricas y morfológicas, se recomienda zonificar el mdt con el objeto de representar las condiciones del terreno, los cuales en áreas extensas evidentemente varía debido a tipo de vegetación de la zona y morfología del río.
Respecto al tiempo de llegada de la avenida a la ciudad de Ambato, no se presentan mayores discrepancias, por lo cual, el tiempo que tarde en la onda en recorrer la longitud aproximada de 36.2 kilómetros, desde presa Mulacorral hasta alcanzar el puente Jaramillo, es de 2 horas 20 minutos con un caudal pico de 1200 m3/s.
Es importante indicar que, el mdt utilizado para el mallado debe ser validado con el fin de evitar estancamientos de agua que produzcan una disminución en el caudal pico del hidrograma de llegada, así como también retardos de la avenida. Es desacertado trabajar con una mallado fino en un mdt de baja calidad.
A futuro, con base en este estudio, se puede profundizar en el análisis incluyendo en los escenarios, otros factores que generen o incidan en la rotura de la presa, como: cambio climático, eventos hidrológicos o eventos sísmicos.