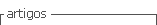1. INTRODUCCIÓN
Las ondas de choque y la interacción de la capa límite turbulenta están presente en los flujos de gas a alta velocidad, para un flujo interno o externo. Una onda de choque se produce por un cambio brusco de la presión de un fluido gas en contacto con un cuerpo que se desplaza a una velocidad mayor a la velocidad del sonido. En la región del choque, las magnitudes termodinámicas de temperatura, densidad, entre otros parámetros, varían drásticamente.
En la literatura están reportados trabajos sobre la capa límite de flujo compresible (White, 1991), donde las curvas teóricas de la ley de pared y de la ley logaritmo son comparados con datos experimentales de velocidad la capa límite con diferentes condiciones de gradiente de presión (Schlichting, 1979); la teoría de las ondas de choque normal, oblicuas y de las ondas expansivas de Prandtl-Meyer ((Anderson, 2007); (White, 2008)); la teoría de la turbulencia (Kármán, 1937); el modelado de la turbulencia (Wilcox, 2006); así como, el principio y aplicaciones de la dinámica de fluidos computacional (CFD, por sus siglas en inglés) ((Blazek, 2015);(Anderson et al., 2012)).
Una de las maneras de estudiar el comportamiento del campo de flujo compresible a velocidad subsónica, transónica y supersónica es mediante el empleo de equipos experimentales, tales como los difusores y las toberas; donde, por las variaciones de la densidad del flujo, las formas de las ondas de choque y las turbulencias son captadas en imágenes mediante la técnica Schlieren. La técnica Schlieren fue propuesto por el físico alemán August Toepler en 1864 (Krehl y Engemann, 1995) y fue el primero en visualizar la geometría de la onda de choque; y esta técnica se emplea de manera recurrente para visualizar el campo de flujo.
Un tipo de difusor transónico, clasificado como modelo G, también conocido como difusor Sajben, inicialmente fue empleado por (Sajben et al., 1981) para realizar ensayos experimentales de flujos transónicos con presencia de choque débil para el flujo con
Posteriormente, el difusor transónico fue empleado por (Sajben et al., 1983), quien utilizó un velocímetro laser Doppler para medir la velocidad del flujo en diferentes regiones. (Bogar et al., 1983) estudió el flujo temporal e inestable en función del número de Mach en secciones transversales a lo largo del difusor; además, (Bogar, 1986) realizó también mediciones con un velocímetro laser Doppler al campo de flujo.
Se señalan a algunos autores de trabajos relevantes que han empleado la geometría del difusor transónico Sajben para simular el campo de flujo aplicando la CFD, para evaluar diferentes modelos de turbulencia y comparar los resultados numéricos con datos experimentales: (Liou et al., 1981) emplearon el método hibrido MacCormack’s y el modelo original de Wilcox-Rubesin para representar la viscosidad de remolino; (Hsieh et al., 1987) utilizaron una versión modificada del método hibrido MacCormack`s, así como, el modelo de Wilcox-Rubesin, y simularon el campo de flujo con el código NASA-ARC-Cray/XMP; (Georgiadis et al., 1994) emplearon el código PARC, y para la simulación de la turbulencia del flujo utilizaron los modelos: Thomas, Baldwin-Lomax, MMLT, Chien
La CFD ha alcanzado gran aceptación en las simulaciones del campo de flujo compresible, empleando el modelo de las ecuaciones de Navier-Stokes de número de Reynolds promedio (RANS, por sus siglas en inglés), el cual requiere de modelos de turbulencia.
Los modelos de turbulencia permiten reproducir la turbulencia del flujo en dominios computacionales que tienen geometrías complejas, por lo cual, determinan las magnitudes de los parámetros termodinámicos que no es posible obtener por medios experimentales. Son tomados en cuenta de acuerdo al comportamiento del régimen de flujo, y de las condiciones de gradientes adversos de presión y de otros parámetros termodinámicos del fluido, dentro y fuera de la capa límite, antes y después del choque. Con el pasar de los años, se han formulado nuevos modelos de turbulencia y, en base a esto, de manera recurrente, se continúa evaluando diferentes modelos de turbulencia para determinar cuáles de los modelos tienen las mejores prestaciones en reproducir diferentes condiciones del régimen del flujo para diferentes casos en específicos.
En el presente trabajo, el objetivo es evaluar cinco modelos de turbulencia para el flujo de aire para
En la sección 2 se presentan las ecuaciones empleadas, el dominio computacional, el dominio mallado y el método de solución computacional. En la Sección 3 se exponen los resultados obtenidos y las discusiones. En la sección 4 se exponen las conclusiones del análisis realizado.
2. METODOLOGÍA
2.1 Fundamento matemático
En el presente trabajo, para la solución numérica del campo de flujo compresible se empleó el modelo RANS.
Las ecuaciones gobernantes empleadas, son: la Ecuación (1) de la conservación de la masa, la Ecuación (2) de la cantidad de movimiento, la Ecuación (3) de la conservación de la energía y la Ecuación (4) de estado. La simulación computacional se consideró para flujo en estado estacionario, y las ecuaciones antes mencionadas en su forma compacta, se expresan como
Donde, la densidad es
Donde, la presión es p; el tensor de tensiones
Donde, la energía total es
Donde, la constante del gas es
La Ecuación (5) de relaciones de presión, y la Ecuación (6) de relaciones de temperatura, se expresan como
Donde, la presión total es
La Ecuación (7), es la variación de la viscosidad para gases en función de la temperatura, se expresa como un aproximado de acuerdo a la ley de Sutherland (White, 2008)
Siendo la viscosidad de referencia
Los cinco modelos de turbulencia empleados en la simulación del flujo, los cuales fueron ensamblados de manera individual al modelo RANS, son las siguientes:
Los modelos de turbulencias, son ecuaciones de transporte semiempírica que modelan el mezclado y difusión que se incrementan a causa de remolinos turbulentos, los cuales están en función de la viscosidad del fluido y de la viscosidad turbulenta, entre otras variables. (Wilcox, 2006) reporta diferentes modelos de turbulencia, y cuyas formulaciones semiempírica están sustentadas en base a las primeras investigaciones de la turbulencia desarrolladas por (Kolmogorov, 1941) en base a los resultados de Reynolds en 1883.
2.2 Dominio computacional
El dominio computacional 2D de la geometría del difusor transónico experimental, modelo G (Sajben et al., 1981), que se consideró para el estudio del flujo, se muestra en la Figura 1. La pared inferior tiene una base recta en toda su longitud, y en la pared superior es recta en los extremos y, en la parte media es curva.
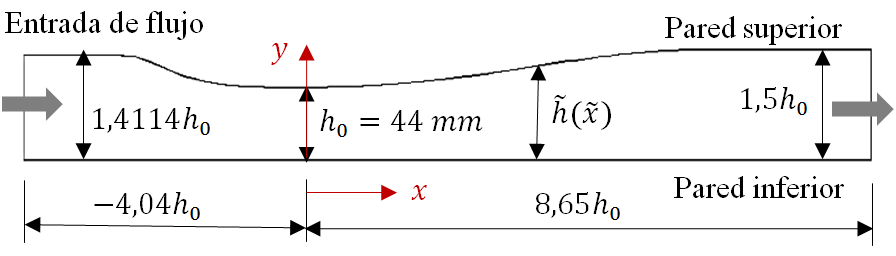
Figura 1. Geometría del dominio computacional del difusor transónico. Construido a partir del esquema reportado por (Sajben et al., 1981).
Las restricciones para las condiciones de borde (C.B.) en el dominio computacional se señalan en la Figura 2. Se estableció para dos casos: un caso para el flujo con onda de choque débil y el otro caso para el flujo con onda de choque fuerte.
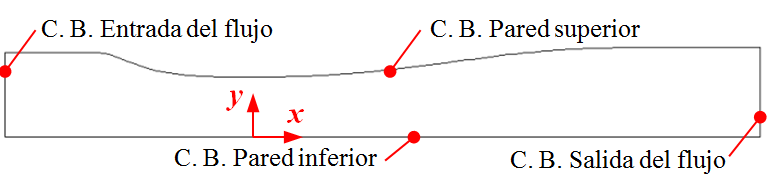
Figura 2. Condiciones de borde en las paredes, en la entrada y salida del flujo en el dominio computacional 2D.
Condiciones de borde aplicadas para el flujo con onda de choque débil, para
Presión de entrada:
Temperatura de entrada:
Presión de salida:
Temperatura de salida:
Condiciones de borde aplicadas para el flujo con onda de choque fuerte, para
Presión de entrada:
Temperatura de entrada:
Presión de salida:
Temperatura de salida:
Para ambos casos, la velocidad del flujo en las paredes es nula, por la condición de no deslizamiento. Además, las paredes se consideraron adiabáticas.
Cabe señalar, los datos de presión para el caso del flujo con onda de choque débil y choque fuerte fueron obtenidos del trabajo de (Bogar et al., 1983), y la temperatura total 300 K (540 R) del trabajo de (Georgiadis et al., 1994).
2.3 Mallado del dominio
El dominio computacional mallado se muestra en la Figura 3. Se aplicó una tecnología de mallado estructurado con celdas cuadriláteras, en la dirección horizontal 179 celdas y en la dirección vertical 100 celdas, para un total de 17900 celdas cuadriláteras; siendo un mallado final luego que se refinó tres veces. Se refinó las regiones adyacentes a las paredes superior e inferior con mayor densidad de celdas, por la presencia del esfuerzo cortante y de la capa límite, así como, se refinó la región donde se presenta la onda de choque. El dominio se discretizó mediante la interacción ICEM-CFD, en la plataforma ANSYS-Meshing.
Cabe resaltar, el estudio de independencia de mallado para los tres casos de refinamiento de la malla, consistió en tomar en cuenta como parámetro de control la caída de presión en la pared inferior, para el flujo con
En la Tabla 1 se presenta la cantidad de celdas de la malla para los tres casos de estudio: 15300 celdas, 16625 celdas y 17900 celdas; así como las caídas de presión; en la Figura 4 se muestra una gráfica correspondiente a los datos de la Tabla 1.
Se determinó el error porcentual, considerando como valor fijo para la caída de presión para la malla con 17900 celdas, para cada modelo de turbulencia, en función de las presiones con menor densidad de malla. El error porcentual para SST
En base a los resultados numéricos de los errores porcentuales, las tres mallas están refinadas con alta densidad en las paredes del difusor transónico; donde, la densidad para los tres casos de mallado en un dominio 2D se obtuvo
Tabla 1. Densidad de la malla, para el flujo con
|
Celdas: |
15300 |
16625 |
17900 |
|
|
Relación de presión, |
||
|
SST |
0,4258087 |
0,4258120 |
0,425815 |
|
|
0,3911357 |
0,3911364 |
0,391137 |
|
|
0,4085790 |
0,4085800 |
0,408581 |
|
|
0,3726328 |
0,3726361 |
0,372639 |
| RSM |
0,3965598 |
0,3965625 |
0,396565 |
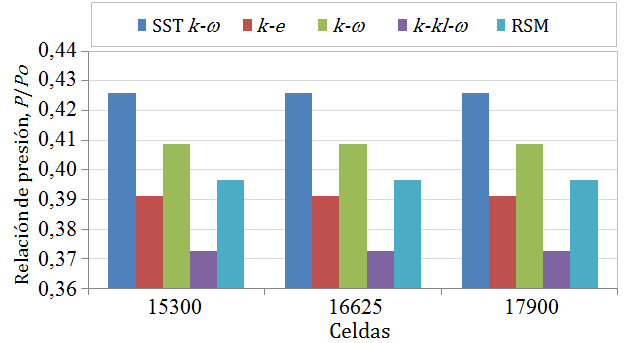
Figura 4. Caídas de presión versus densidad de la malla, evaluados para cinco modelos de turbulencia. Gráfica correspondiente a los datos numéricos de la Tabla 1.
2.4 Método de solucíón computacional
Se empleó el código ANSYS-Fluent Versión 12.1 que aplica el método de volumen finito (MVF) para las simulaciones numéricas. Dentro de las diferentes alternativas de solución, se seleccionó la opción de análisis basado en densidad para fluido compresible; dominio 2D en el plano cartesiano; sustancia de trabajo: aire. Para cada simulación se empleó un solo modelo de turbulencia, en el siguiente orden: SST
Para el procesamiento de datos de la simulación del flujo, se empleó un equipo con las siguientes características: Laptop marca Síragon, modelo M54R, Intel Core 2 Duo, dos procesadores de 1,8 GHz, y memoria RAM de 3 GB.
3. RESULTADOS Y DISCUSIÓN
En esta sección, para el régimen del flujo con onda de choque débil para
3.1. Campo de densidad y número de March
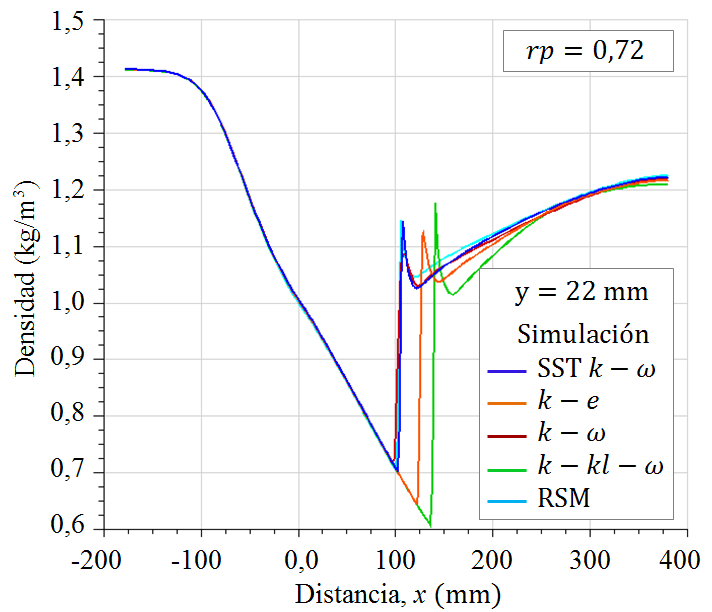
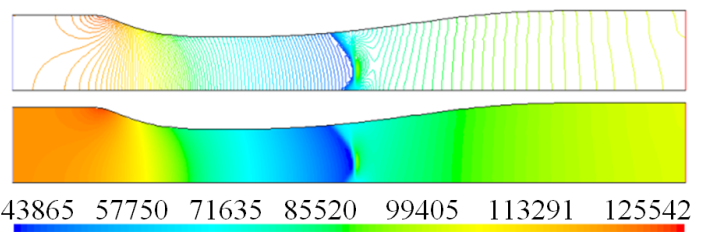
Las simulaciones numéricas de las distribuciones de la densidad del flujo, para el flujo con relación de presión
Las variaciones de la densidad en el campo de flujo muestran en que regiones el flujo está comprimido y descomprimido, para el flujo de aire con choque débil, para
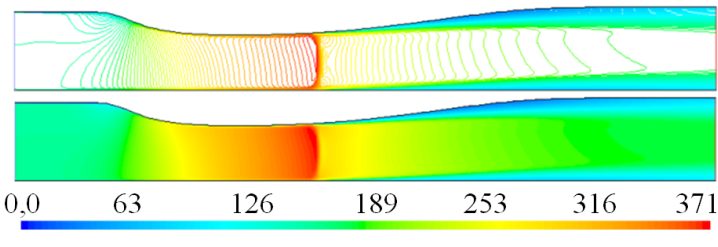
Así mismo, para la densidad flujo de aire con choque fuerte para
Al comparar, ambos casos del flujo, para
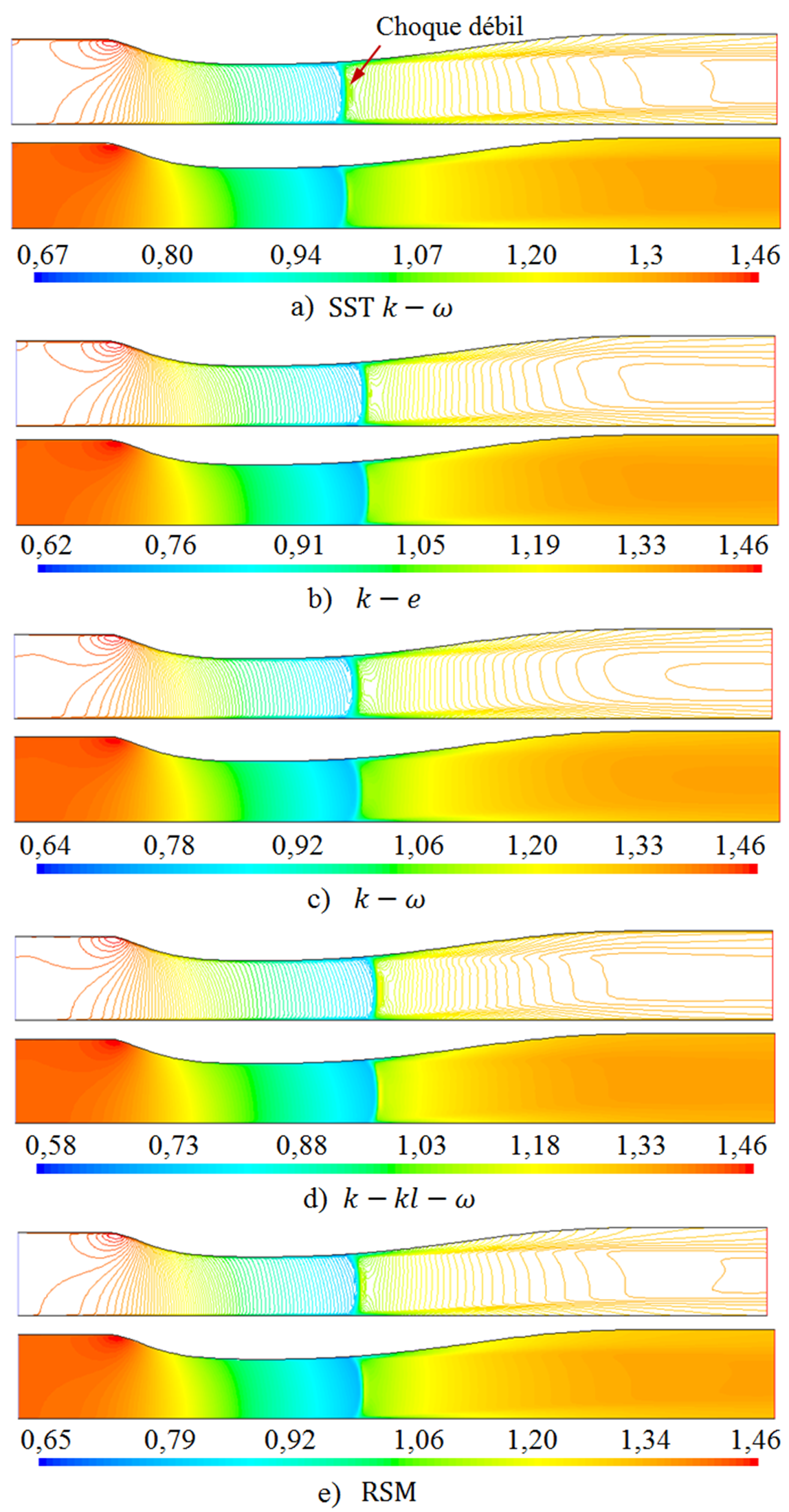
Figura 5. Campo de densidad (kg/m3), para el flujo con
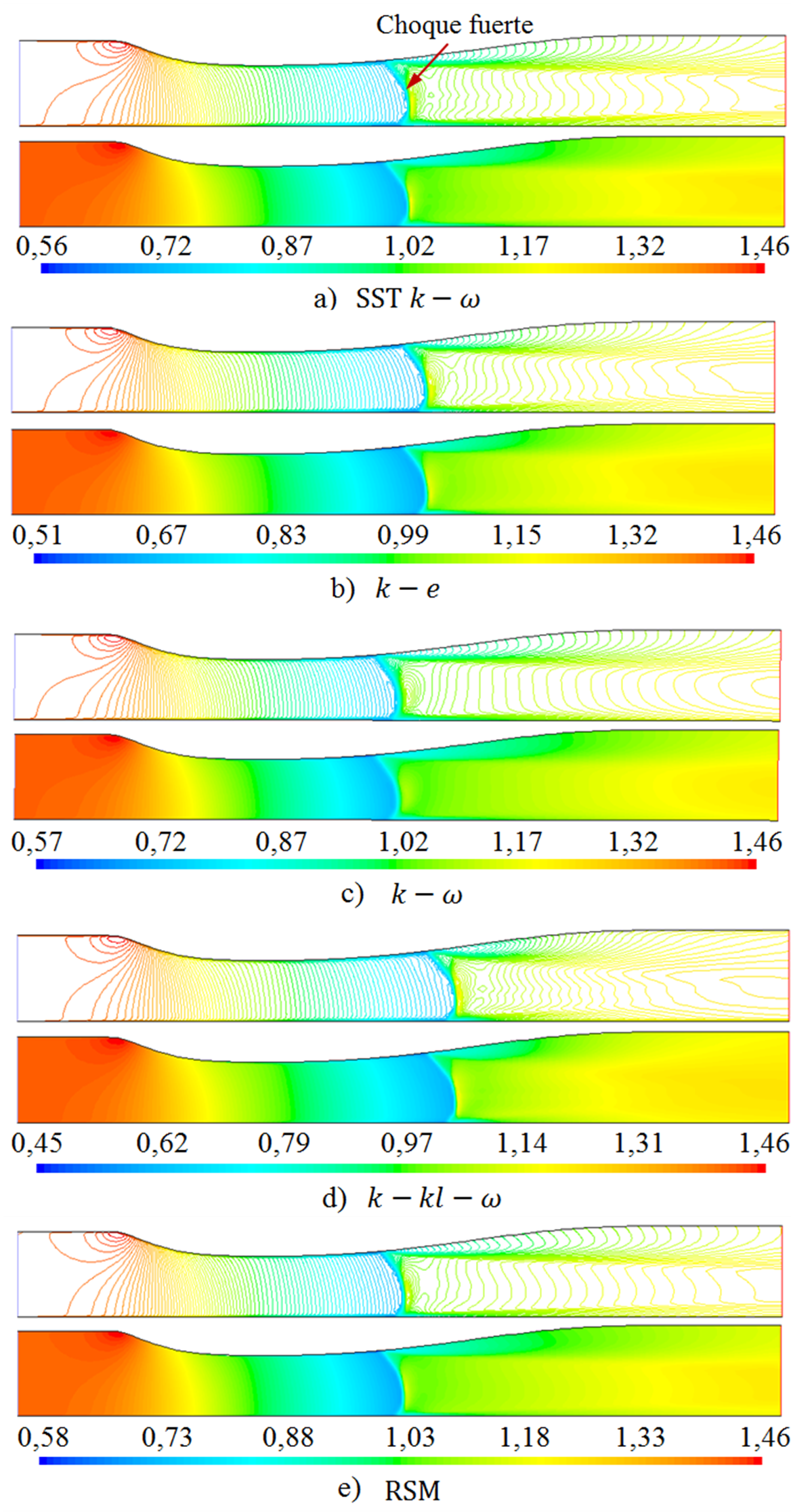
Figura 6. Campo de densidad (kg/m3), para el flujo con
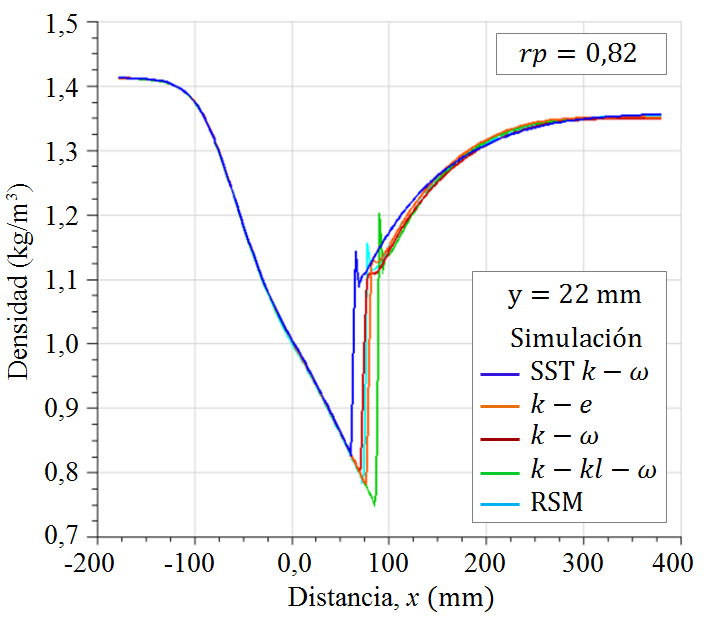
Los perfiles de densidad evaluados a lo largo de todo el difusor transónico, para los cinco modelos de turbulencia, para la altura de
El comportamiento de las trayectorias de las curvas muestra la variación de la magnitud de la densidad antes y después del choque. Para el flujo con
Para el flujo con
La magnitud de la densidad en el instante del inicio y al final del choque, tanto como su posición, para el flujo con
El menor espesor de la onda de choque débil de magnitud 5,280 mm, se obtuvo para
Las posiciones para las distancias adimensionales, para el flujo con
Tabla 2. Densidad, para el flujo con
|
|
Inicio del choque |
|
Final del choque |
|
|
|
x 1 (mm) |
Dens. (kg/m3) |
x 2 (mm) |
Dens. (kg/m3) |
|
SST |
62,304 |
0,8243 |
67,584 |
1,1394 |
|
|
76,388 |
0,7835 |
83,424 |
1,1316 |
|
|
69,344 |
0,8034 |
81,664 |
1,1111 |
|
|
85,184 |
0,7513 |
90,464 |
1,2036 |
| RSM |
72,864 |
0,7864 |
78,144 |
1,1575 |
Tabla 3. Densidad, para el flujo con
|
|
Inicio del choque |
Final del choque |
||
|
|
x 1 (mm) |
Dens. (kg/m3) |
x 2 (mm) |
Dens. (kg/m3) |
|
SST |
102,78 |
0,7039 |
108,06 |
1,1450 |
|
|
122,14 |
0,6432 |
129,18 |
1,1242 |
|
|
97,504 |
0,7182 |
108,06 |
1,0858 |
|
|
136,22 |
0,6079 |
141,50 |
1,1784 |
|
|
101,02 |
0,7038 |
106,30 |
1,1479 |
Tabla 4. Densidad, para el flujo con
|
|
|
|
||
|
|
|
|
|
|
|
SST |
5,280 |
0,3151 |
5,280 |
0,4411 |
|
|
7,036 |
0,3481 |
7,040 |
0,4810 |
|
|
12,32 |
0,3077 |
10,556 |
0,3676 |
|
|
5,280 |
0,4523 |
5,280 |
0,5705 |
|
|
5,280 |
0,3711 |
5,280 |
0,4441 |
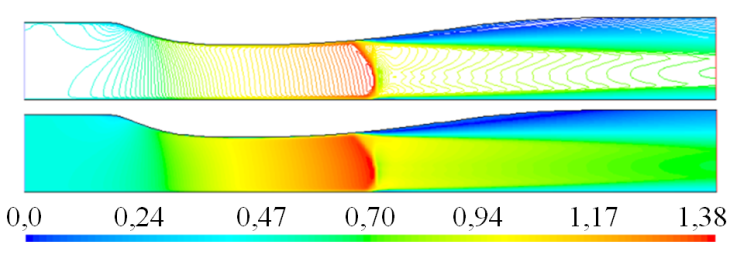
La distribución de número de Mach para el flujo con
El comportamiento de la trayectoria del perfil para el número de Mach, para la altura
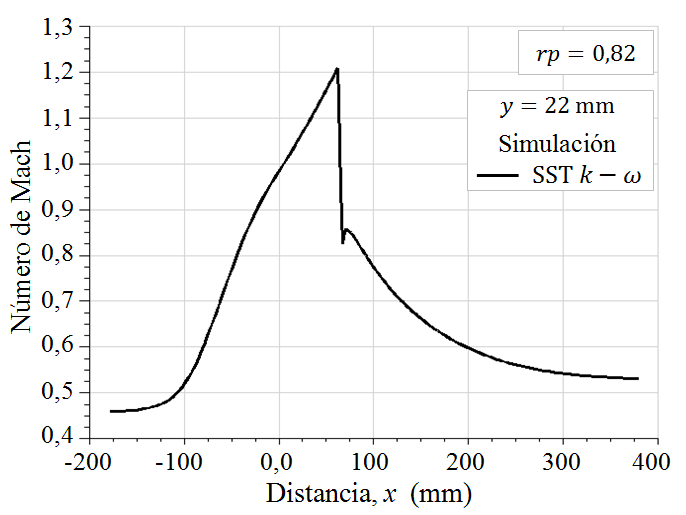
El flujo con choque débil para
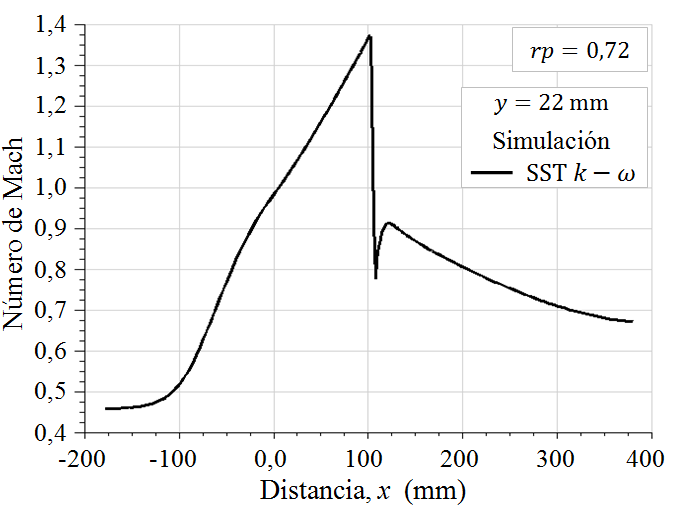
Así mismo, para el flujo con choque fuerte para
La imagen de la forma de la onda de choque débil y fuerte obtenido con el modelo de turbulencia SST
Tabla 5. Número de Mach, para el flujo con choque débil y choque fuerte; para la altura
|
|
Inicio del choque |
Final del choque |
||
|
|
x 1(mm) |
Mach |
x 2 (mm) |
Mach |
|
|
62,304 |
1,2105 |
67,584 |
0,8264 |
|
|
102,78 |
1,3733 |
108,06 |
0,7782 |
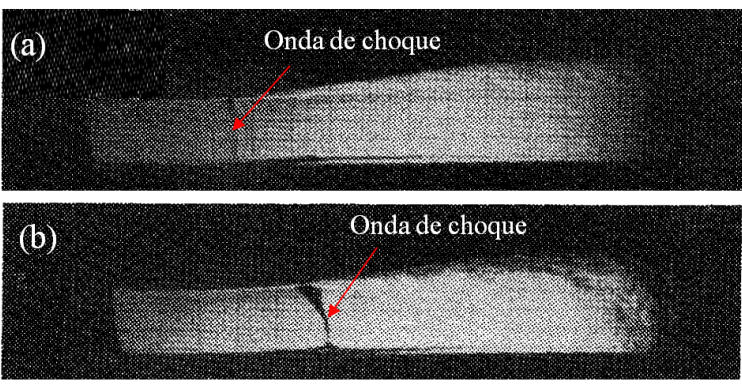
Figura 13. Experimento: imagen captada con la técnica Schlieren. (a) Onda de choque débil: Mach = 1,235 para
Cabe señalar, los resultados numéricos de los espesores de la onda de choque podrían estar desviados en términos estadísticos para
3.2. Campo de presión estática
Las simulaciones numéricas de perfiles de presión estática, empleando los cinco modelos de turbulencia:
Para la presión del flujo con
Para el flujo con
El dato de la presión experimental para el flujo con
Para los otros modelos de turbulencia:
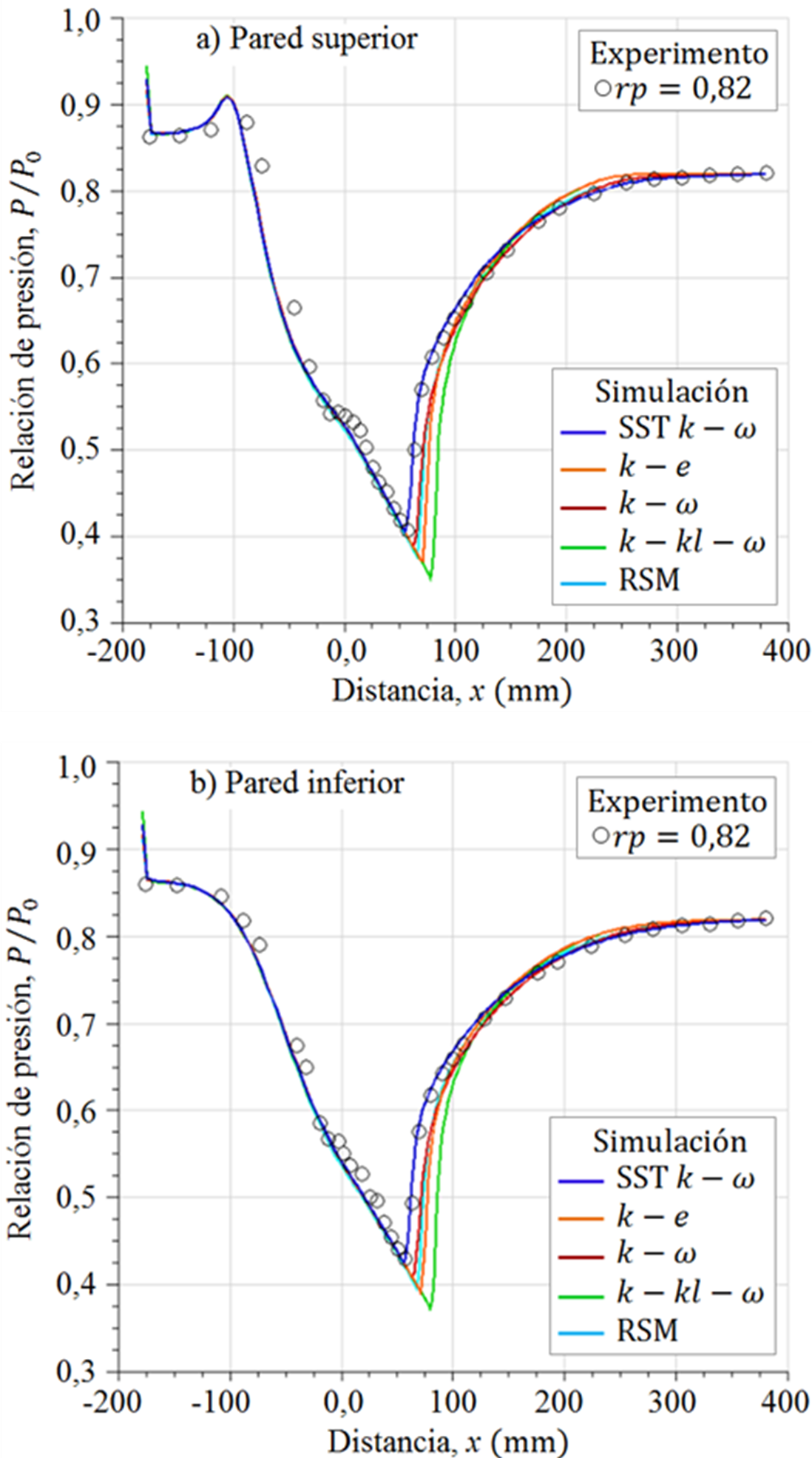
Figura 14. Perfiles de presión estática, para el flujo con
Al igual que en el caso anterior, se tiene para el flujo con
Los resultados del modelo de turbulencia
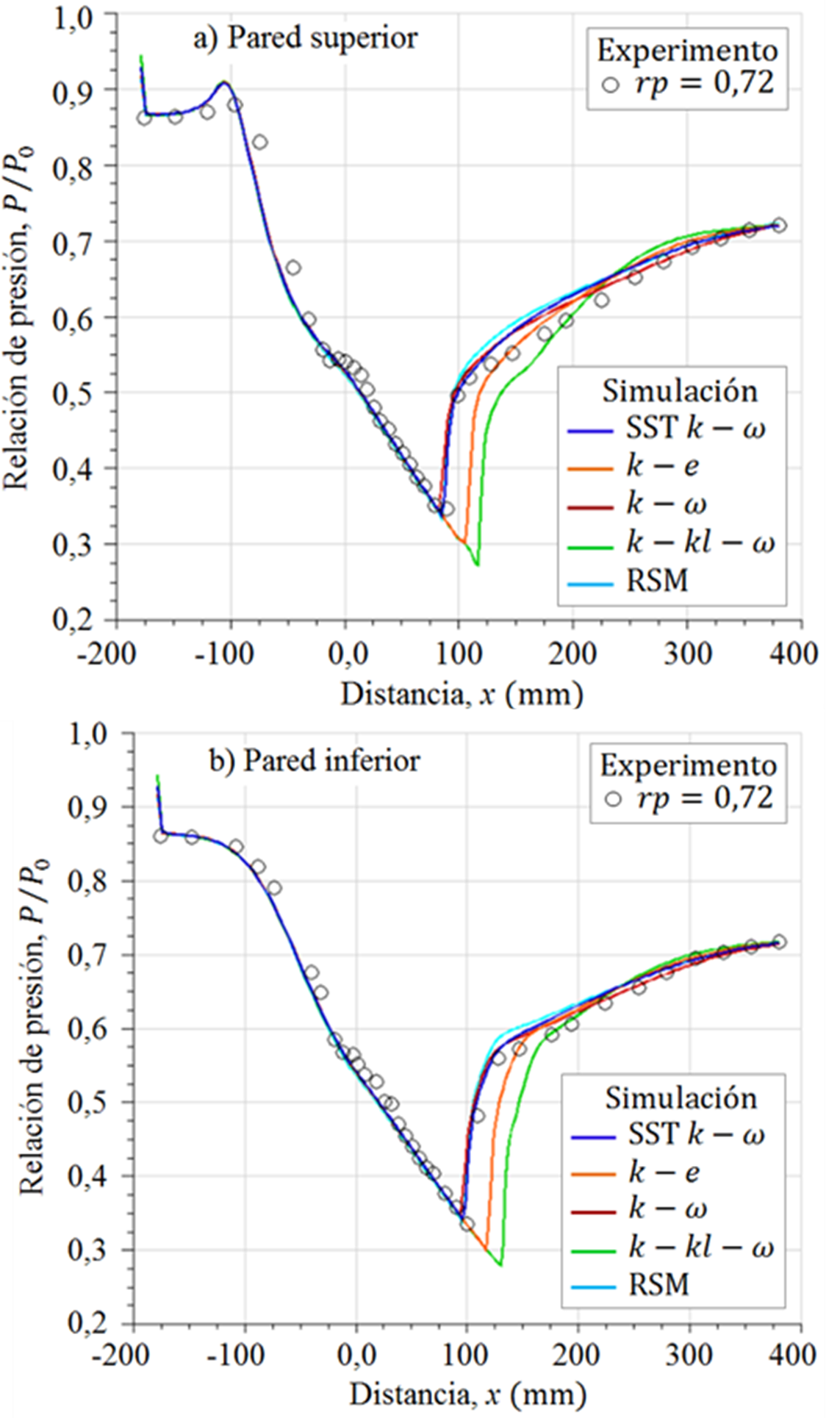
Figura 15. Perfiles de presión estática, para el flujo con
Los otros modelos de turbulencia:
Tabla 6. Datos de posición y de presión en la pared superior.
|
|
x (mm) |
|
P (Pa) |
|
Experimento: |
56,76 |
0,408 |
55081,672 |
|
SST k-ω |
55,264 |
0,405452 |
54737,682 |
|
|
71,104 |
0,371812 |
50196,144 |
|
|
62,304 |
0,389813 |
52626,353 |
|
|
78,144 |
0,351237 |
47418,435 |
| RSM |
65,824 |
0,377098 |
50909,776 |
Tabla 7. Datos de posición y de presión en la pared inferior.
|
|
x (mm) |
|
P (Pa) |
|
Experimento: |
57,20 |
0,430 |
58051,763 |
|
SST k-ω |
57,024 |
0,425815 |
57486,770 |
|
|
71,104 |
0,391137 |
52805,098 |
|
|
64,064 |
0,408581 |
55160,110 |
|
|
79,904 |
0,372639 |
50307,792 |
| RSM |
67,584 |
0,396565 |
53537,900 |
Tabla 8. Datos de posición y de presión en la pared superior.
|
|
x (mm) |
|
P (Pa) |
|
Experimento: |
88,88 |
0,346 |
46711,418 |
|
SST k-ω |
85,184 |
0,338552 |
45705,908 |
|
|
106,30 |
0,302356 |
40819,299 |
|
|
81,664 |
0,346256 |
46745,979 |
|
|
116,86 |
0,273588 |
36935,501 |
| RSM |
85,183 |
0,334489 |
45157,386 |
Tabla 9. Datos de posición y de presión en la pared inferior.
|
|
x (mm) |
|
P (Pa) |
|
Experimento: |
99,44 |
0,335 |
45226,373 |
|
SST k-ω |
95,744 |
0,342981 |
46303,841 |
|
|
116,86 |
0,300379 |
40552,396 |
|
|
93,984 |
0,347829 |
46958,341 |
|
|
130,94 |
0,280320 |
37844,349 |
| RSM |
95,742 |
0,338622 |
45715,358 |
Tabla 10. Error porcentual con respecto a la posición experimental.
|
|
Posición: error porcentual, % |
|||
|
|
|
|
||
|
|
P. sup. |
P. inf. |
P. sup. |
P. inf. |
|
SST |
2,635 |
0,307 |
4,158 |
3,716 |
|
|
25,271 |
24,307 |
19,599 |
17,518 |
|
|
9,764 |
12,000 |
8,118 |
5,486 |
|
|
37,674 |
39,692 |
31,48 |
31,677 |
|
|
15,968 |
18,153 |
4,159 |
3,718 |
Tabla 11. Error porcentual con respecto a la caída de presión.
|
|
Presión: error porcentual, % |
|||
|
|
|
|
||
|
|
P. sup. |
P. inf. |
P. sup. |
P. inf. |
|
SST |
5,708 |
0,973 |
1,060 |
2,382 |
|
|
13,532 |
9,037 |
9,744 |
10,334 |
|
|
9,345 |
4,981 |
3,360 |
3,829 |
|
|
18,316 |
13,339 |
18,331 |
16,322 |
|
|
12,302 |
7,775 |
0,152 |
1,081 |
Del análisis realizado, el modelo de turbulencia de
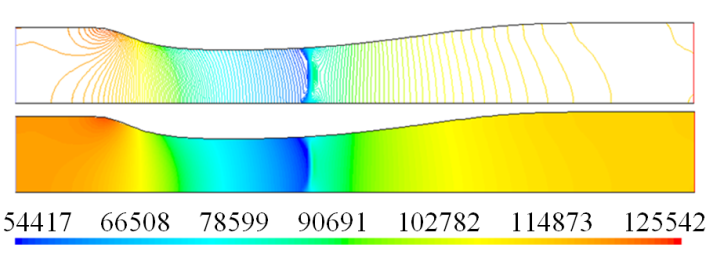
En las Figura 16 y Figura 17 se muestra la distribución de presión estática en diferentes regiones del campo de flujo, así como, en las regiones donde se presenta las ondas de choque. Para la altura
Cabe resaltar, se refinó la malla a lo largo de la pared para reducir a la mínima expresión los errores numéricos para la presión, en las paredes del difusor, por lo cual, la densidad de la malla se obtuvo para
3.3. Campo de velocidad
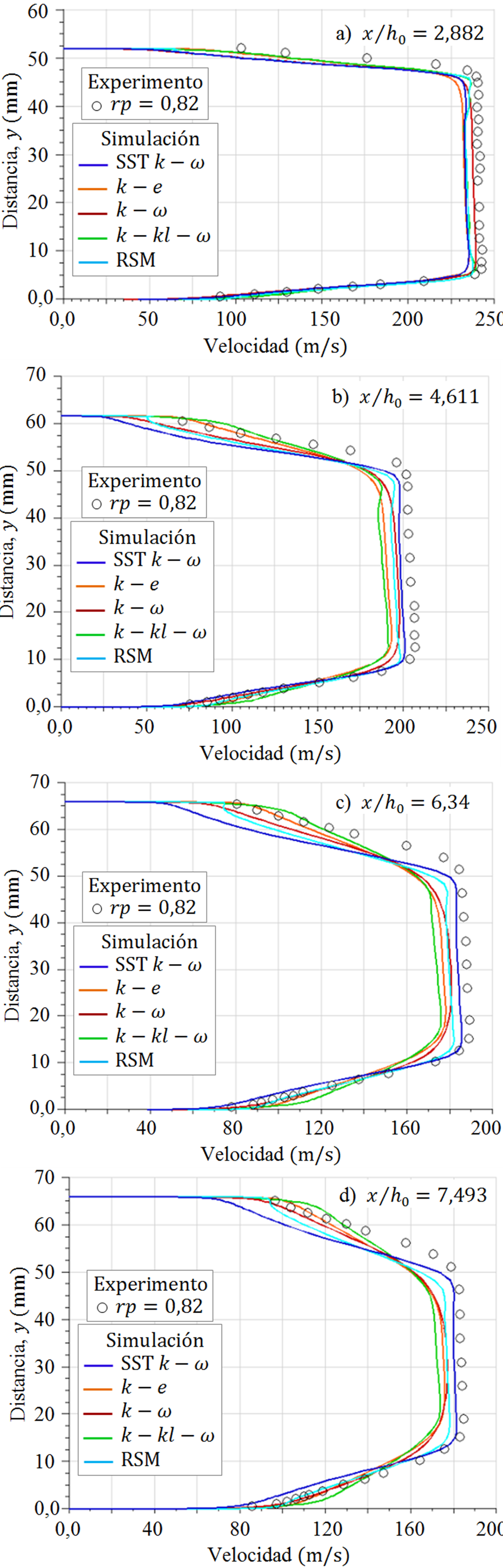
Los perfiles de velocidad del flujo para diferentes tramos a lo largo del difusor transónico, para
La posición de la velocidad del flujo para
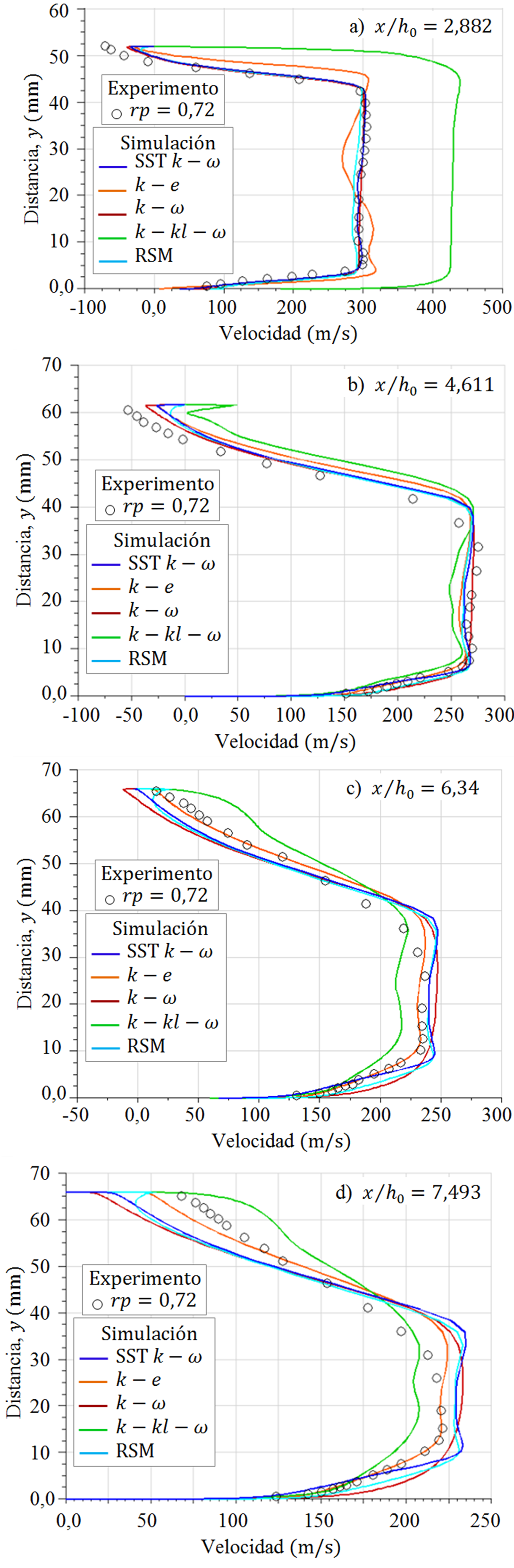
Así mismo, para el flujo con
Tanto para el flujo con onda de choque débil para
Cabe destacar, en la pared superior, para la posición
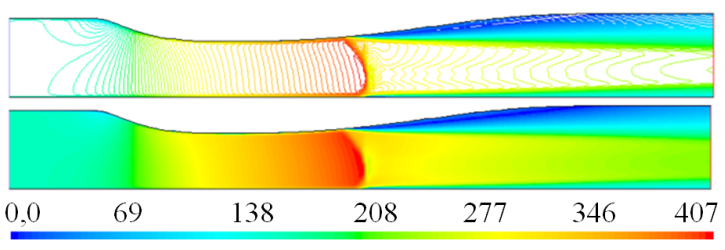
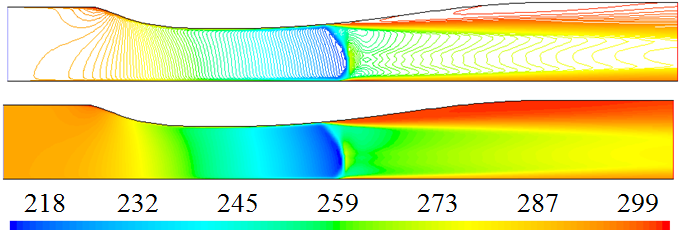
3.4. Campo de temperatura estática
La simulación del campo de temperatura estática para el flujo con
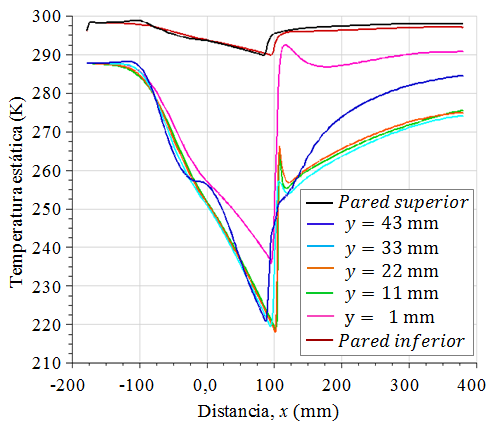
Los perfiles de temperatura estática en la dirección x se muestran en las Figura 24 y Figura 25, para el flujo con
Para la altura
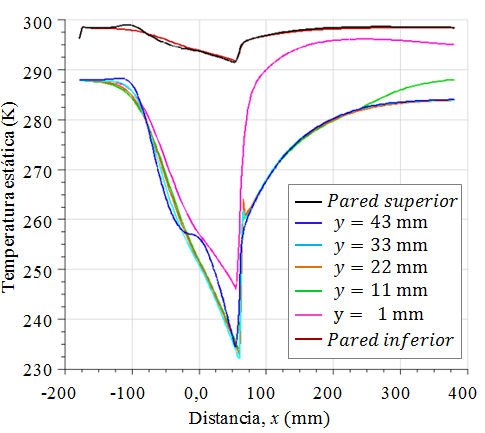
Figura 24. Perfiles de temperatura estática, para el flujo con
4. CONCLUSIONES
En base a los resultados obtenidos de la simulación del flujo para los cinco modelos de turbulencia:
Los resultados numéricos obtenidos tienen que ver con los fundamentos matemáticos de cada modelo de turbulencia y el método de evaluación que aplican en la región dentro y fuera de la capa límite. Ya que, dentro de la capa límite, para la región del flujo adyacente a la pared están presente el esfuerzo cortante; y existen dos parámetros de interés, el espesor y el coeficiente de fricción, tanto para flujo laminar o turbulento. Los modelos de turbulencia tienen divergencias en los resultados numéricos cuando se produce la separación del flujo de la pared, pues, seguidamente del punto de separación, está presente una región del flujo con sentido inverso, presentando velocidades negativas. Cuando son comparados con datos experimentales de presión y de velocidad, ciertos tramos de las curva numéricas están próximas y otras alejadas de los datos experimentales. Por lo cual, se considera que se debe evaluar los cinco modelos de turbulencia para un dominio 3D, de esa manera, tener un criterio de evaluación más amplio con respecto al desarrollo del flujo después que se presenta el choque. Sin embargo, de los cinco modelos de turbulencia empleados, el que más se ajusta a los datos experimentales de densidad, número de Mach, presión y velocidad, es el modelo de turbulencia
Además, en base a los resultados obtenidos con el modelo de turbulencia
El espesor de la onda de choque para el flujo con
Para el caso de número de Mach, que fue comparado el resultado numérico con el experimental, al inicio del choque para el flujo con
Para la presión, al inicio y final de la onda de choque, para el flujo con
La velocidad el flujo, el inicio y final de la onda de choque, para el flujo con
Para la temperatura estática, para el flujo con